双后掠乘波体高超声速试验与数值分析

2022-10-14刘传振孟旭飞刘荣健白鹏

航空学报 2022年9期

刘传振,孟旭飞,刘荣健,白鹏

中国航天空气动力技术研究院,北京 100074

乘波体概念自提出以来,因其高超声速阶段的高升阻比特性吸引了人们的广泛关注。1959年,Nonweiler首先提出了楔形流场乘波体,1960年代,Jones等使用锥形流场进行设计,有效提高了容积率,后续有研究使用其他的基准流场,比如攻角锥、椭圆锥流动、一般三维流动等,扩大了设计空间。

1990年,Sobieczky等提出密切锥方法,提高了设计灵活性,有效扩大了设计空间,可以生成很多具有特殊性质的乘波体。其中,给定平面形状设计乘波体成为密切锥方法发展的重要方向。2005—2011年,洛马公司的Rodi从密切锥方法出发,提出了定后掠角乘波体,为定平面形状乘波体的设计提供了思路。段焰辉等给出了定后掠角乘波体的具体实现。Konstantinos等实现了给定三维前缘线的乘波体设计。设定乘波体的平面形状,有望改善乘波体的性能缺陷,比如低速性能不好、纵向稳定性不足等,生成具有良好宽速域性能的外形,具有良好的应用潜力。Zhao等等根据Rodi的方法生成一种尖头后掠乘波体外形,结合涡升力改善了低速性能。笔者也提出过一种双后掠乘波体,发现这种外形在保证高超声速高升阻比的同时,低速性能较好,纵向稳定性也有所提升。

乘波体性能的验证之前主要通过计算流体力学(Computational Fluid Dynamics, CFD)手段,流场模拟表明乘波体下表面的流动很好地复现了基准流场,而且性能也可达到预期。但仅有数值模拟无法完全确定性能分析的准确度,有学者开展过风洞试验,比如针对钝化前缘乘波体、修改上表面扩容的乘波体飞行器、三维流场乘波体等,不过总起来说,这种工作还比较少。

本文在文献[19]的基础上,构建双后掠乘波体风洞试验模型,开展设计马赫数状态的高超声速风洞试验,分析前缘钝化影响、升阻力特性、纵向稳定性等。通过对比不同外形,并结合数值模拟技术,验证设计方法和设计外形的有效性,推进双后掠乘波体的工程实用。

1 外形及模型

1.1 定平面形状乘波体设计

采用由密切锥方法发展的定平面形状乘波体设计方法设计进行风洞试验的外形。在密切锥方法中,有2条设计曲线：激波出口型线(Inlet Capture Curve, ICC),决定了激波的出口形状；流线追踪起始线(Flow Capture Tube, FCT),表示流线追踪的起始投影线。

设计曲线ICC、FCT与所生成乘波体的俯视图平面形状轮廓线(Planform Contour Line, PCL)存在几何关联。选择标准坐标系。ICC、FCT、PCL分别由3个函数、、表示,则函数、、之间的几何关系表达式为

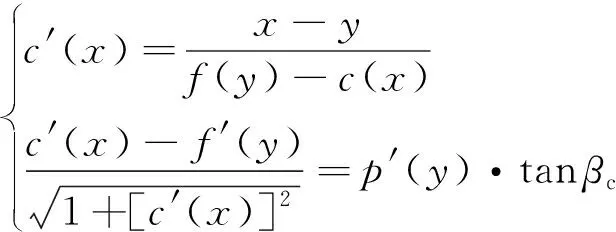
(1)

式中：为锥形流激波角,具体推导可参考文献[23]。ICC、FCT、PCL在半展长处交于一点,因此设定边界条件为()=()=()。

微分方程组(1)建立了密切锥方法的设计参数ICC、FCT与乘波体平面形状PCL之间的几何关系。观察式(1),、为2个未知数,为已知量,根据微分方程理论,只要已知函数、、中的2个,第3个就可以求出。于是存在3种情况：① 已知和,求；② 已知和,求；③ 已知和,求。情况 ①、情况 ③ 就是定制平面形状生成乘波体外形的方法：考虑到函数和是乘波体前缘线分别在正视图和俯视图方向的投影,情况 ② 可以看作给定三维前缘线设计乘波体。式(1)可以通过数值求解,具体见文献[23]。

1.2 双后掠乘波体风洞试验模型

根据式(1)生成双后掠乘波体外形。具体做法是事先给定一个双后掠平面形状轮廓线PCL,并将FCT设定为水平直线,求解式(1)得到ICC；再将ICC、FCT作为设计曲线输入密切锥方法,即可获得给定双后掠平面形状的乘波体外形。

分别设计了弯头双后掠(BEND)、尖头双后掠(CUSP)乘波体外形开展数值模拟和风洞试验。BEND外形在马赫数=5状态下设计,2个后掠角分别为73°、50°,设计激波角=15°。

图1(a)给出了BEND外形的设计曲线FCT、ICC,其中为翼展,为飞行器外形高度。ICC通过求解式(1)得到,外形如图1(b) 所示。CUSP外形在=8状态下设计,2个后掠角分别为75°、50°,头部尖锐。为了与BEND外形有相似容积率,设计激波角=12°。

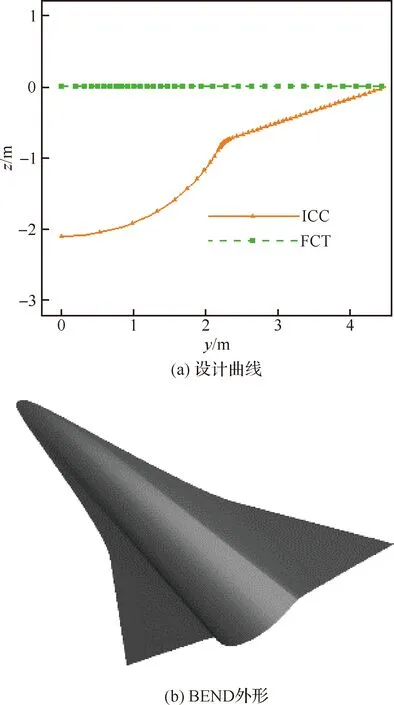
图1 生成BEND外形的设计曲线Fig.1 Design curves of BEND configuration

为了对比,增加一个单后掠乘波体SINGLE。SINGLE与CUSP外形类似,设计状态=8,外形头部尖锐,与CUSP有相同的长度和平面投影面积,后掠角为63.5°。为了保证与CUSP外形具有相同的容积率(容积的2/3次方与平面投影面积的比值),调整=11.15°。3个外形的尺寸见表1,试验和计算的参考面积与参考长度均为各自外形的平面投影面积和全长。

由这3个外形的数模设计加工风洞试验模型,材质为不锈钢,并增加支杆配合天平安装。天平使用常规内式六分量测力天平,设计载荷和校准度相对误差如表2所示,、、,、、分别为机体坐标系3个方向的力和力矩,‰FS为校准量程的千分比。

表1 试验外形的尺寸Table 1 Geometry parameters of configurations

表2 天平设计载荷和校准相对误差Table 2 Design load and calibration of balance

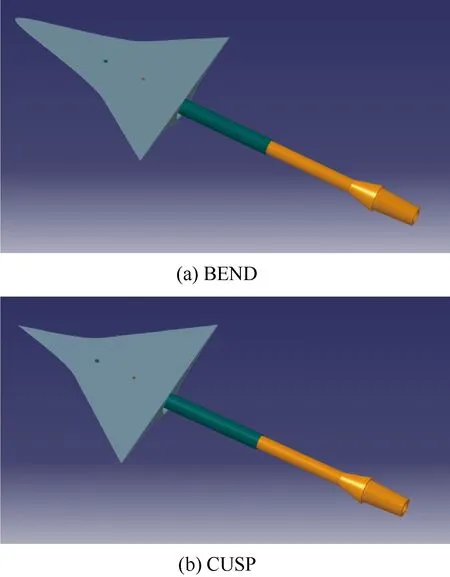
理论乘波体前缘尖锐,在实际生产中不可能实现,本文使用文献[24]中的方法,将上表面抬高以钝化前缘,钝化半径为0.5 mm。3个风洞试验模型如图2所示,带支杆和天平。

2 分析方法

2.1 风洞试验

高超声速试验在中国航天空气动力技术研究院的FD-07风洞中进行。FD-07风洞为暂冲、吹引式高超声速风洞,以空气为工作介质。带封闭室的自由射流试验段为1 880 mm×1 400 mm×1 130 mm。马赫数=4～8,喷管出口直径0.5 m (马赫数=4喷管出口直径0.4 m),采用更换喷管的方法改变马赫数,=6以上喷管带有水冷装置,防止喷管结构受热喉道产生变形。试验段侧壁开有通光口径为∅350 mm光学玻璃窗口,供纹影仪观察和拍摄流场使用。

试验设置=4.937, 7.960,马赫数及对应的具体试验状态见表3,表中为总压,为总温,为雷诺数,为等价高度。状态=4.937 及其对应的压力、温度、高度等参数,可看作BEND外形的设计马赫数状态,=7.960则为CUSP、SINGLE外形的设计马赫数状态。另外,这些状态的0°攻角可以看作相应外形的设计状态。

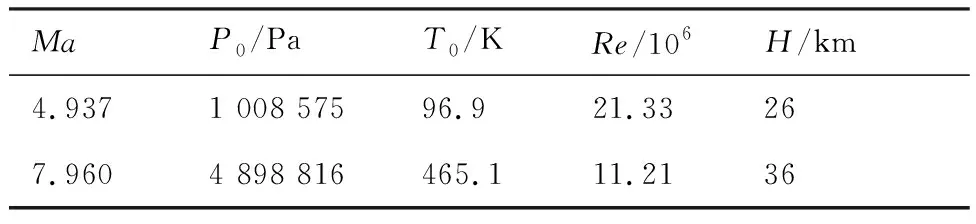
表3 高超声速风洞试验状态Table 3 Experiment states in hypersonic wind tunnel

图3为试验模型安装在风洞试验段的实物照片,试验模型攻角范围由天平量程决定,=4.937 状态下的BEND模型的试验攻角范围较小,为0°～8°,间隔2°；在=7.960状态,CUSP、SINGLE模型的试验攻角范围分别为0°～20°、0°～18°,间隔2°。

图3 风洞试验模型Fig.3 Experimental models in wind tunnel

2.2 数值模拟

由于天平量程的限制,风洞试验未能测试太多状态,且风洞试验难以捕捉很多流场特征,因此增加数值模拟手段分析气动性能和流场特征作为补充。数值方法采用有限体积方法求解三维可压缩Navier-Stokes方程。无黏通量采用Roe格式计算,有权重格林-高斯公式重构方法获得空间二阶精度,梯度限制器选取改进的Barth限制器,以消除计算中间断附近的数值过冲和振荡,同时应用基于压力辅助限制器的局部熵修正方法避免非物理解。黏性通量采用二阶中心格式计算。湍流模型采用在工程上广泛应用的Menter SST (Shear Stress Transfer)-两方程模型。时间方向采用二阶精度双时间步方法,LU-SGS (Lower-Upper Symmetric Gauss-Seidel) 隐式推进求解。

采用分区结构化网格,如图4所示,保证激波与黏性流动的精确模拟。在激波间断位置网格尽量顺激波方向布置；黏性层法向网格尽量保证垂直壁面,流向参数梯度较大位置保证足够的流向网格密度。

图4 近壁面处的计算网格Fig.4 Computation mesh near the wall

以图2中的CUSP风洞试验模型为例,验证网格无关性。生成3套不同密度的网格：稀疏网格Coarse,网格量3.2×10；中等密度网格Medium,网格量6.4×10；密网格Refined,网格量9.6×10。表4给出在=7.960风洞试验状态下攻角=10°的升阻力系数,Δ、Δ分别为使用Coarse、Medium网格计算的气动力相比Refined网格的相对误差,可以看到3套网格计算的升阻力系数很接近,升阻比也近乎相等。表4中同时给出了摩擦阻力系数vis的值,Δvis为使用Coarse和Medium网格计算的摩擦阻力系数相比于Refined网格的相对误差,可以看到这3套网格计算的摩阻系数也很接近。考虑到不管对于升阻力系数还是摩阻系数,Medium网格与Refined网格的误差更小,可以认为Medium网格,网格量在6 400 000左右,是可信和足够的。

表4 CUSP模型的网格无关性(Ma=7.960, α=10°)

3 气动力性能

3.1 钝化影响

前缘钝化对乘波体性能影响很大,本节使用CFD技术,分析前缘钝化对升阻比的影响。首先考察BEND模型,对比无钝化理论乘波体外形和钝化前缘的试验模型在状态=4.937 下的升阻比。图5(a)给出升阻比()随攻角的变化,曲线“Theoretic”表示理论设计的尖锐前缘乘波体,“Blunted”表示钝化后的试验模型,理论乘波体最大升阻比为2°攻角时的4.03,风洞试验模型最大升阻比为4°攻角时的3.62,0.5 mm半径的前缘钝化使最大升阻比降低了0.41。

图5(a)中的“Blunted-NL”指钝化试验模型扣除钝化前缘之后的升阻比,其升阻比曲线与“Theoretic”非常接近。图5(b)为理论乘波体和钝化试验模型只统计上下表面的升阻比数据,对“Theoretic”来说,相当于整个乘波体外形扣除底面气动力,对“Blunted”来说,则是扣除底面和前缘钝化部分,两者计算结果很接近,在2°攻角时得到最大升阻比,均大于5.0。这说明钝化导致的升阻比损失主要由钝化部件本身带来,而钝化带来的流场变化对其他部件的气动力影响相对较少。

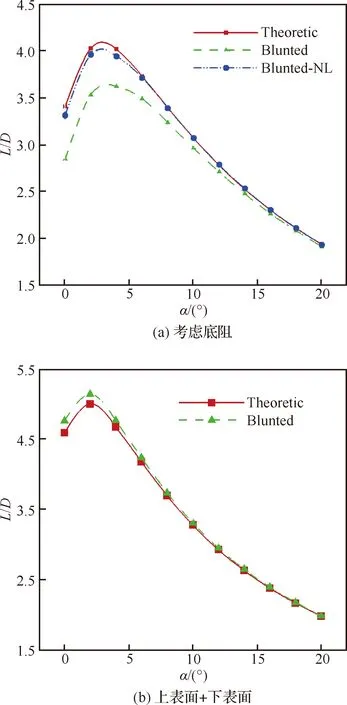
图5 理论乘波体与钝化前缘BEND模型升阻比(Ma=4.937)Fig.5 L/D ratios of theoretic and blunted leading-edge BEND model (Ma=4.937)

下面考察CUSP模型。在=7.960状态对比理论乘波体和钝化前缘模型的升阻比曲线。图6为升阻比随攻角的变化,理论乘波体最大升阻比为2°攻角的3.89,钝化试验模型最大升阻比为4°攻角的3.28,0.5 mm前缘钝化使最大升阻比降低了0.61。而钝化试验模型扣除钝化前缘后的升阻比曲线,同样与理论乘波体非常接近。

进一步比较理论乘波体和钝化试验模型,只统计上下表面的升阻比数据,两者很接近,最大升阻比约为2°攻角时的4.3,这也说明钝化导致的升阻比损失主要由钝化部件本身带来,而钝化带来的流场变化对其他部件的气动力影响较少。

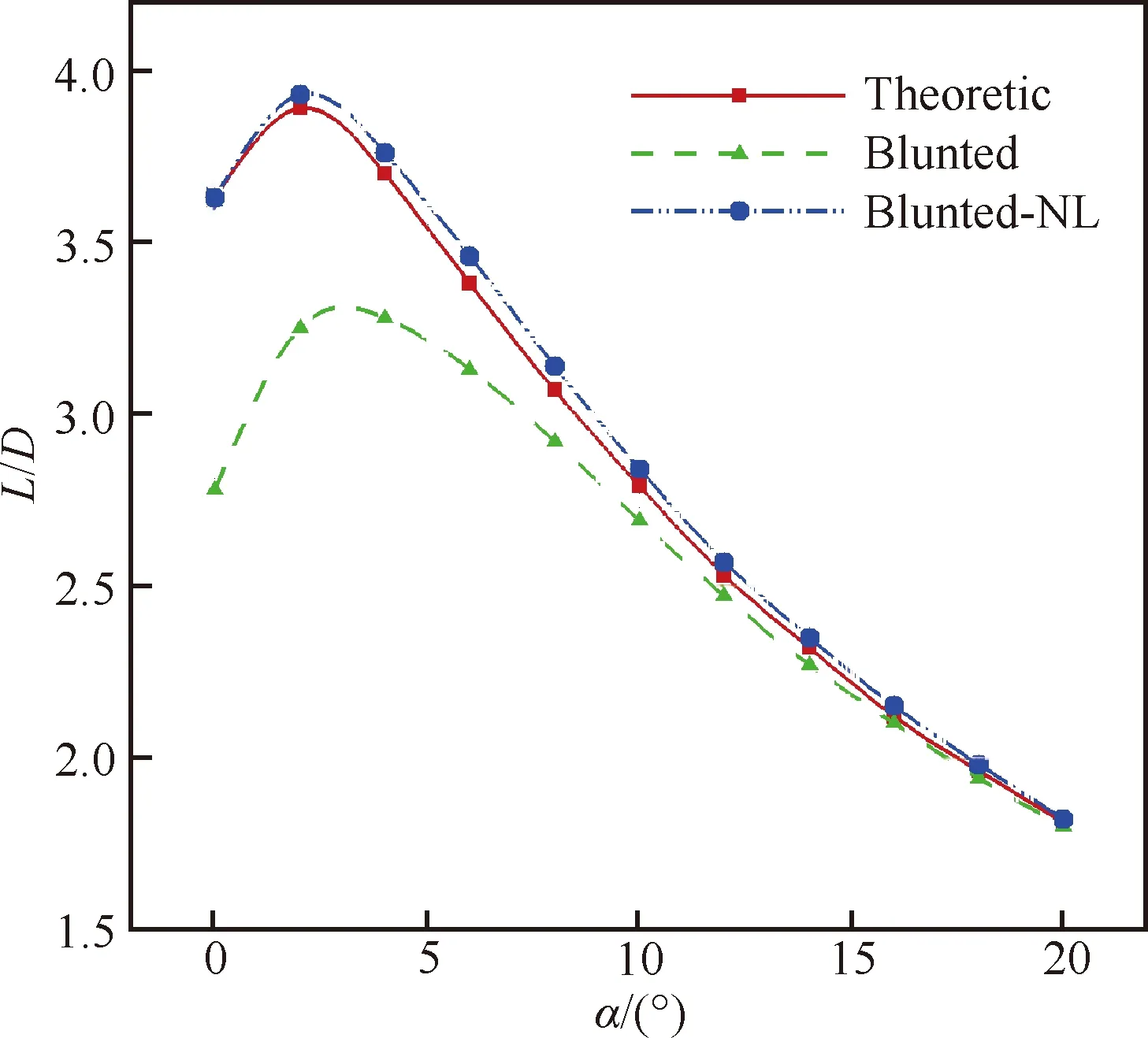
图6 理论乘波体与钝化前缘CUSP升阻比(Ma=7.960)Fig.6 L/D ratios of theoretic configuration and blunted-leading-edge CUSP model (Ma=7.960)

综合这2类外形,可以看到0.5 mm的钝化半径对气动性能影响很大,使升阻比降低了0.5左右。针对长度300 mm左右的乘波体,0.5 mm的钝化半径相当于长度30 m的飞行器使用50 mm 的钝化半径,在实际的飞行器设计中一般不使用这么大的钝化半径,尤其是非驻点前缘部分,因此本次试验的结果较为保守。

3.2 设计状态性能分析

表5给出3个模型分别在设计状态时的升阻力。在风洞试验中,BEND模型在=4.937,=0°时升阻比为2.958；CUSP、SINGLE模型设计状态近似为=7.960,=0°,升阻比分别为2.782、3.234。CFD结果与风洞试验误差较小,升阻比的相对误差均小于1%。

考虑到钝化和底面阻力的影响,风洞试验模型的升阻比与理论乘波体相比下降明显。表6给出了CFD计算的3个模型扣除钝化和底部部件气动力后在设计状态时的气动力性能,BEND、CUSP、SINGLE的升阻比为4.76、4.17、4.66,相比于表5,3个模型扣除钝化和底部部件气动力后升阻比均较高。

表5 设计状态升阻力对比

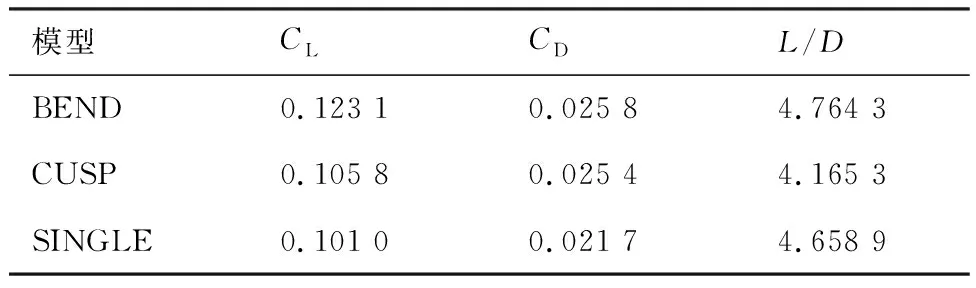
表6 CFD计算的扣除底部和钝化部件的气动力

图7(a)给出了BEND模型在设计状态(=4.937,=0°)后缘截面(=320 mm)的压力分布,下表面激波很明显。而且,ICC曲线除了在激波转折较大的地方与激波有较大偏差外,大部分区域都与激波形状吻合。当然,由于前缘钝化存在,气流到上表面的泄露比较明显。图7(b)为对称面处的压力分布,图7(c)为风洞试验纹影图,可以看到通过CFD模拟得到的激波形状与风洞试验纹影图中非常类似,说明弯头双后掠乘波体保持了良好的“乘波”效应。

图7 BEND模型的CFD流场和纹影图像(Ma=4.937, α=0°)Fig.7 CFD flow fields and schlieren photograph of BEND model (Ma=4.937, α=0°)

图8(a)给出了CUSP模型在设计状态(=7.960,=0°)后缘截面(=289 mm)的压力分布,可以看到下表面的激波很明显,而且ICC曲线的大部分区域与激波形状吻合；由于前缘钝化存在,高压气流从下表面到上表面有一定泄露。图8(b)为对称面处的压力分布,图8(c)为风洞试验纹影图,CFD结果与风洞试验拍摄的激波形状吻合良好。这一结果同样说明,尖头双后掠乘波体也保持了良好的“乘波”效应。

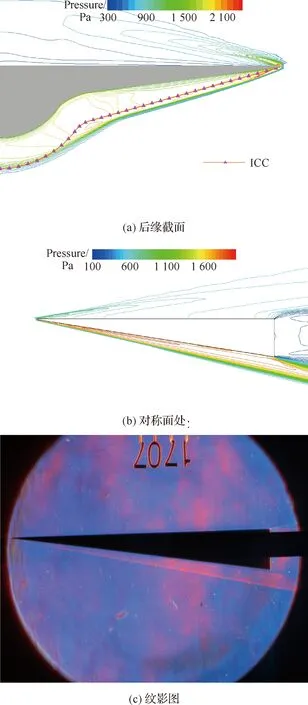
图8 CUSP模型的CFD流场和纹影图像(Ma=7.960, α=0°)Fig.8 CFD flow fields and schlieren photograph of CUSP model (Ma=7.960, α=0°)

3.3 升阻力随攻角的变化

图9给出了BEND模型在=4.937时CFD计算和风洞试验(Wind Tunnel Test,WT)测量的升阻力数据。相比于风洞试验,CFD计算的气动力均略小,而升阻比略高。最大升阻比在=4°取得,CFD结果为3.62,风洞试验为3.58,相对误差为1.11%。

图10给出CUSP模型的升阻力数据,小攻角时(<10°),CFD计算的升阻力与风洞试验数据很接近,其中升力相对误差小于2.5%,阻力小于2%。但随着攻角增大,误差增大,在20°时升力相对误差5.74%,阻力为5.14%。大攻角时误差较大,原因可能是数值计算无法精确捕捉背风面分离流动,具体还需要细致分析。

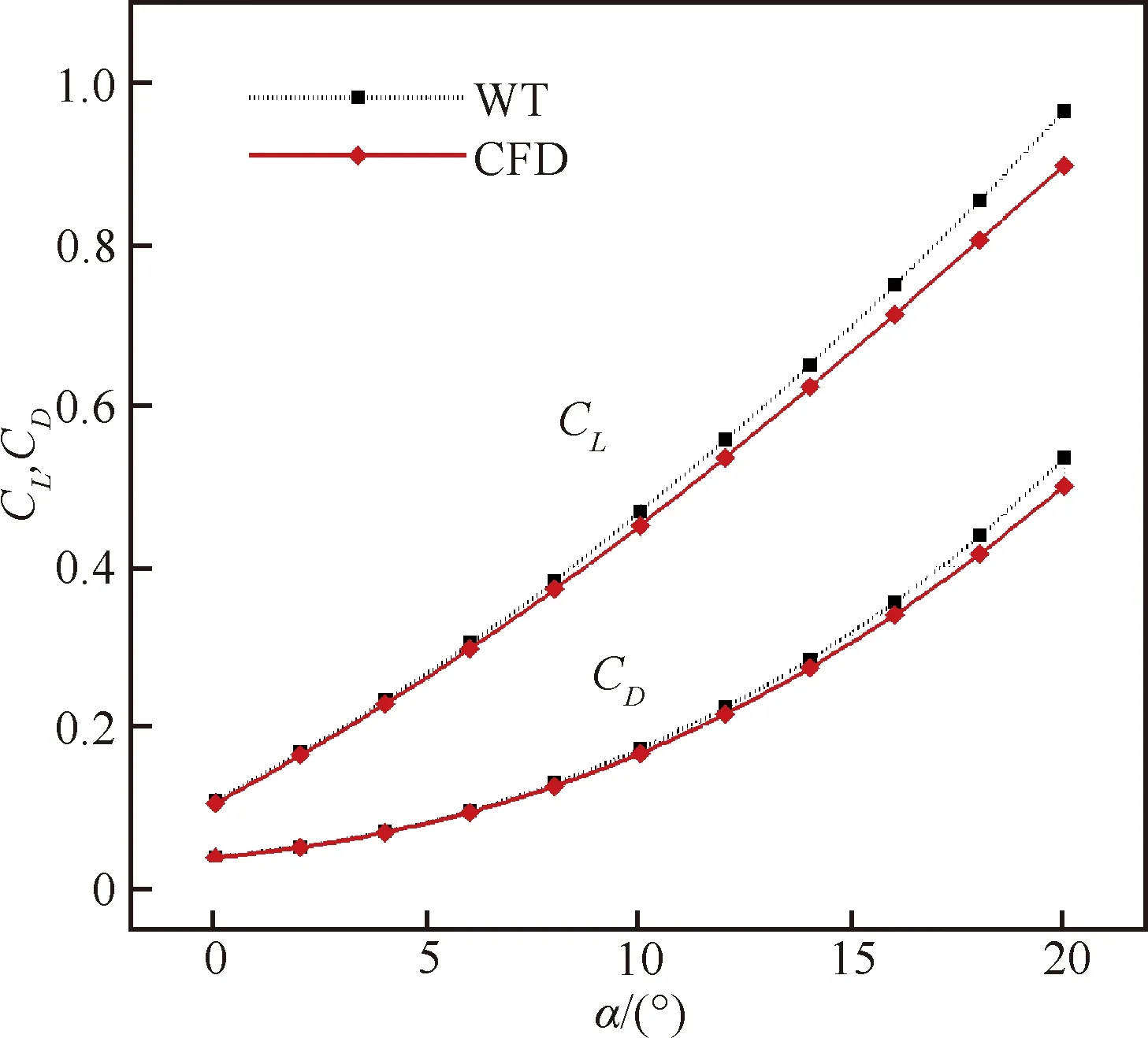
升阻比则在0°～20°攻角范围内均吻合良好,误差不超过1%。最大升阻比在4°攻角取得,CFD计算结果为3.28,风洞试验测量结果为3.31,CFD结果相对风洞试验的误差为0.82%。

分析SINGLE模型的气动力数据,发现在整个攻角范围内,CFD结果相对风洞试验测量的升阻力误差很小,其中升力相对误差小于1.5%,阻力相对误差小于2.5%。升阻比也很接近,如图11 所示,最大升阻比在=2°取得,CFD计算结果为3.75,风洞试验测量结果为3.80,CFD结果相对风洞试验的误差为1.3%。

图11 SINGLE模型升阻比随攻角的变化(Ma=7.960)Fig.11 L/D ratios of SINGLE vs angle of attack (Ma=7.960)

CUSP和SINGLE模型的设计状态相同状态设计,平面投影面积、容积率也相同,但SINGLE的升阻比比CUSP要高。图12给出=7.960,=4°时使用CFD计算的CUSP和SINGLE下表面压力分布,与SINGLE相比,CUSP的压力较高,在第2后掠区域的前缘线附近存在明显的高压区,这可能是导致阻力增大、升阻比下降的原因。

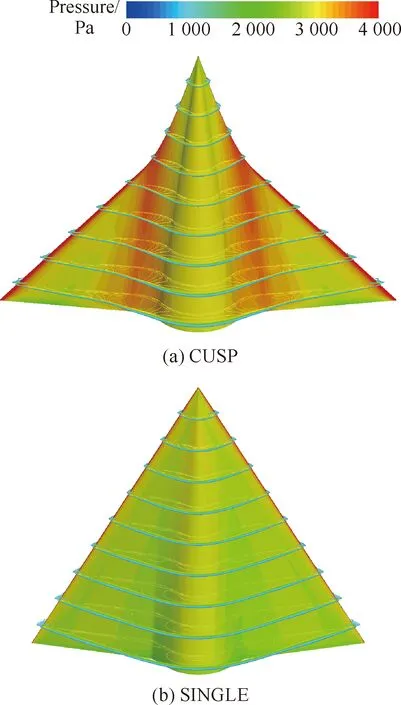
图12 SINGLE、CUSP模型下表面压力分布 (Ma=7.960, α=4°)Fig.12 Pressure distributions of SINGLE, CUSP (Ma=7.960, α=4°)

4 纵向稳定性

飞行器的俯视图平面形状对纵向稳定性影响很大,文献[18]初步探讨了双后掠乘波体在纵向稳定性方面的优势。本节将结合风洞试验和CFD结果,进一步验证稳定性优势。

将重心设定在离头部2/3全长处。图13为BEND模型在=4.937时俯仰力矩系数和气动焦点(Aerodynamic Center, A.C)随攻角的变化。风洞试验只能测量攻角0～8°,相对于风洞试验,CFD计算得到的俯仰力矩系数最大误差在=8°攻角取得,为0.002；A.C的最大误差在=6°时取得,为全长的0.65%。相比于气动力,风洞试验与CFD计算得到的纵向稳定性差别较大,但趋势是准确的。

结合风洞试验和CFD计算的俯仰力矩结果可以看出,弯头双后掠乘波体为纵向静稳定,且气动焦点位置在70%全长以后,稳定裕度较大。

图13 BEND模型纵向稳定性(Ma =4.937)Fig.13 Longitudinal stability of BEND (Ma=4.937)

图14为CUSP、SINGLE模型在=7.960时、A.C随攻角的变化。对CUSP模型来说,当攻角<10°时,CFD计算得到的相对于风洞试验结果的误差较小；而>10°后,误差随攻角增大而增大,最大误差为=20°时的-0.013。与类似,CFD计算得到的A.C相对于风洞试验结果的误差也随攻角增大而增大,最大误差为全长的2.2%,在=20°时取得。CFD和风洞试验得到的纵向稳定性在大攻角时差别较大,与升阻力类似,原因可能与数值计算无法精确捕捉背风面分离流动有关。虽然大攻角时差别较大,但总的趋势是一致的：尖头双后掠乘波体为纵向静稳定,且气动焦点均在全长的72%之后,稳定裕度较大。

图14 CUSP、SINGLE模型纵向稳定性(Ma=7.960)Fig.14 Longitudinal stability of CUSP, SINGLE (Ma=7.960)

对SINGLE模型来说,CFD结果和风洞试验数据差别较大,由图14(b)启动焦点位置图所示,风洞试验得到的A.C在2/3全长之前,而CFD计算的A.C则在2/3全长之后,二者差值为全长的1%～2%。这也导致图14(a)中SINGLE的风洞试验结果为纵向静不稳定,而CFD结果为纵向小静稳定。

不管是CFD结果还是风洞试验结果,综合比较图14 中的CUSP、SINGLE模型,双后掠外形的纵向静稳定性比单后掠外形都有很大提高,说明平面投影面积相等时,双后掠有利于增强纵向静稳定性。查看图12中的压力分布,可以看到相比于SINGLE,CUSP后半部分面积较大,而且压力也较高,导致压力中心后移,以及气动焦点位置后移,使稳定性增强。

考虑到3.3节中分析的CUSP模型的升阻比较SINGLE模型低,可以初步认为双后掠乘波体牺牲了部分高超声速升阻比性能,而提高纵向静稳定性。