基于压电迟滞对称性的线性微位移控制作动器
2022-10-13王荣秀
王荣秀, 王 波
(1.重庆工商大学 人工智能学院, 重庆 400067;2.重庆理工大学 理学院, 重庆 400050)
0 引 言
压电陶瓷由于其独有的优良特性,目前已被广泛地应用于微机构、微电子、精密加工、微光学器件、机器人等多个领域,其中,被大量应用的压电陶瓷微位移定位系统具有分辨率高、输出力较强,且响应快、无噪音、无回程间隙和摩擦等优点,但Shi[1]、Yin[2]等指出由于压电陶瓷存在迟滞、蠕变等非线性特性,而迟滞作为主要的非线性特性严重影响了纳米级驱动系统的运动和定位性能,限制了它在纳米级定位技术中的应用;同时,Quant[3]、Islam[4]及Ronkanent[5]等也认为如果不能找到解决压电迟滞的有效方法,则压电陶瓷非线性特性带来的误差难以消除,从而使其在纳米级微位移系统中失去应用价值。因此,近年来,有许多研究者提出了针对压电作动器迟滞效应的消除或补偿方法。如Islam提出一类位置观察器,利用观察器得到的位移信息来修正压电位移系统的非线性输出;其优点是不需要专用的传感系统,因此容易实现,不足之处是改进效果有限,且观察器本身带来的误差难以排除。Ta[6]采用带记忆功能的神经微网络结构得到了非线性补偿器,使压电位移误差可以控制在μm量级,但其模型工作不稳定、实现难度较大。
通常可将这些消除压电迟滞影响的方法分为两类:一种是建立非线性迟滞模型;另一种是通过控制策略的设计(如闭环控制)来获得对迟滞的补偿。非线性迟滞模型大致又分为微观模型与宏观模型,其中微观模型从物理学基本原理出发,通过研究本构关系来描述压电材料并进而理解迟滞的内在机理[7-8]。如秦海辰[9]通过电磁学基本原理并结合压电方程探讨了压电效应过程中的内能变化,建立了相应的迟滞方程。该方程虽能模拟出压电迟滞行为,却不能动态地描述各回路之间的联系,并且由于在方程的推导过程中对材料的假设过于理想,因此在实际中难以应用。一般来说,产生迟滞的原因十分复杂,因此微观模型不可避免地存在简化、假设等限制,模型描述所需参数较多且不易测定。在这种情况下,作为替换的宏观模型从现象的定量关系描述出发,绕过对材料内部机理的复杂研究,利用输入/输出特性构建数学方程来拟合系统的驱动特性,具备简单、易于建立且方便描述的优点[10-11]。目前流行的宏观模型普遍存在着计算量大、算法较为复杂的不足,如Preisach模型、PI模型及Bouc-Wen模型等[4,10-13]。例如在Preisach模型中,通过引入Preisach算子并采用二次积分的方法来获得不同位移调节状态下的回路面积,从而估算迟滞补偿量。该模型由于采用了二次积分,模型较为复杂、计算量较大;而如果进行简化,则非线性误差得不到有效抑制,且会累积,在实际应用中误差较大。
当通过控制策略的设计来抑制迟滞效应时,最常采用的方法是闭环控制,也就是说获取输出状态量来修正输入,从而逼近所期望的输出,其好处是勿需建立精确的模型,如模糊控制[14]、滑模控制[15]或神经网络控制[16]等。一般来说,反馈控制方法比开环控制方法更可靠,当然也更复杂[17-18]。然而,无论是什么闭环控制系统,由于受控对象本身的不确定性,再加上额外电路导致的不稳定性及复杂性,使控制系统计算量大且容易失效[19-22]。
从现有文献来看,无论是采用迟滞模型还是通过控制策略来消除迟滞影响,虽能改进精度,有些甚至达到nm级,但普遍存在模型复杂、计算量大、控制关系非线性或不稳定等缺点。其根源来自两个方面:一是没有充分利用迟滞行为本身的特点,如对称性或可重复性;二是没有考虑如何消除由于各次级循环回路的出现而导致的复杂性。因此,一种较好的选择是利用迟滞效应中存在的对称性质建立简单有效的模型,同时在控制过程中排除因迟滞回路不同而导致的非线性和复杂性,但这方面的研究还少有报道。
为了得到线性、易于实现且稳定的模型,本文提出依据PZT迟滞回路的轴对称性特点来设计可精确控制位移量的控制系统,并使控制关系线性化。其基本思想是通过固定输入电压的最大/最小值,仅采用一个确定的迟滞主回路,整个驱动调节过程仅沿主迟滞回线的逆时针方向进行,避免各次级回路的出现,以保证对称性的完整,且所确定的主回路可精确近似,从而使控制过程得以大大简化;同时,使用两块独立且性质一致的PZT作动器以完成主回路控制过程,这样不但能有效消除次级回路的出现,而且两块作动器产生的迟滞效应相互抵消,总的位移输出与总的控制电压输入呈线性关系。在对称条件下,PZT作动器的输入可由简单的数学模型计算得到,模型算法简便直接,实验结果证明了其可靠性与有效性。
1 PZT迟滞行为及迟滞回路的对称性
1.1 压电迟滞回路及其对称性
PZT作动器的迟滞行为一般可用电压-位移曲线来描述[5],图1是经过极化处理的PZT-5在不同电压下的迟滞曲线。

图1 压电作动器的迟滞曲线Fig.1 The hysteresis curves of a piezoelectric actuator
图1中,电压从0顺次增至最大时的曲线AbaB与电压由最大值递减至0时的曲线BecA分别称为顺调曲线与逆调曲线。由图中可见,顺调曲线单调增加且下凸,而逆调曲线单调增加且上凸。由顺调与逆调曲线组成的回路AbaBecA构成一个主回路,包围一块面积。任何位于主回路区域之内的回路,如cfBec,可定义为次级回路,它们也有自己电压的最大值与最小值,如图1中的点a和点b。当在最大和最小值之间的电压调向反转时,也就是电压由顺次增加改变为顺次减小或由减小变为增加时,比当前回路更低一级的次级回路就会出现。各次级回路的产生使压电的迟滞行为变得更加复杂和难以描述,但次级回路的产生可通过固定每次调节时的电压最值及调节方向来避免,也就是只在最值处才改变电压由增至减或由减至增的调节方式。例如,通过固定点A和点B,就可以只考虑主回路AbaBecA,电压调节由A增至B点,然后从B点减至A点,完成一次循环。除了简单以外,仅使用一个主回路的优点还在于可以保持顺调曲线与逆调曲线不变。
压电位移控制系统的另一个问题是如何计算所需位移或位置对应的输入电压。主回路的曲线函数可通过实验测定并采用多项式来逼近,但一般得到的电压-位移函数是以电压为自变量,因此当想要通过位移来计算电压时就得知道其反函数关系,但高阶多项式的反函数难以求解。在此情况下,充分利用迟滞回路呈现出来的对称性无疑可使问题得以简化。
从建模的实际角度出发,有两种PZT迟滞回路的对称性可供参考:中心对称性与轴对称性。由于基于中心对称性的模型精度更好而基于轴对称性的模型更容易得到线性的变量关系,因此本文的基本思路是利用轴对称性来建立线性模型,同时采用中心对称性来分析并修正前者的误差。
中心对称性最早由Wang[22]和Ann[23]提出并用于建立他们的压电迟滞模型。在这种条件下,BecA被认为与AbaB相对于回路AbaBecA所围区域的中心点O对称(图1),因此,曲线BecA可由曲线AbaB相对于对称点O通过旋转180°得到。图2中,两条曲线l1和l2相对于点P对称,若已知l1的函数表达式为y=f(x),则由对称性知,l2的函数关系就可表示为y=2Yo-f(2Xo-x),即有l2满足关系2Yo-y=f(2Xo-x),也就是说l2可以用变量2Xo-x及2Yo-y替换l1函数y=f(x)中的x和y。
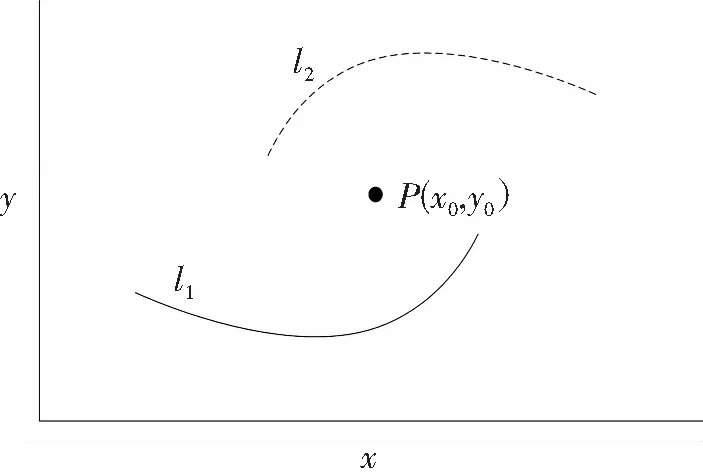
图2 相对于中心点P对称的两条曲线Fig.2 Two curves symmetrical with respect to the center point P
中心模型原理简单,但由于无法排除各次回路,实现过程复杂且计算代价较高。本文提出迟滞回路的轴对称性并用于得到更简单的线性模型。以主回路曲线AbaBecA为例,逆调曲线BecA可认为与顺调曲线AbaB相对于直线段AB对称,如图1所示。如此,则BecA段曲线的函数关系可由AbaB相应的函数表达式经由线段AB对称而得到,反之亦然。下面讨论轴对称模型的基本原理。
1.2 基本数学关系
假设顺调曲线l1与逆调曲线l2对应的函数分别是y=f1(x)与y=f2(x),l是对称轴,φ是对称轴l与x轴之间的夹角,如图3所示。对于对称轴l上的任一点P(X,Y),有Y=Xtanφ。这表明,Y与X呈线性关系,知道了Y,可很容易计算出X。
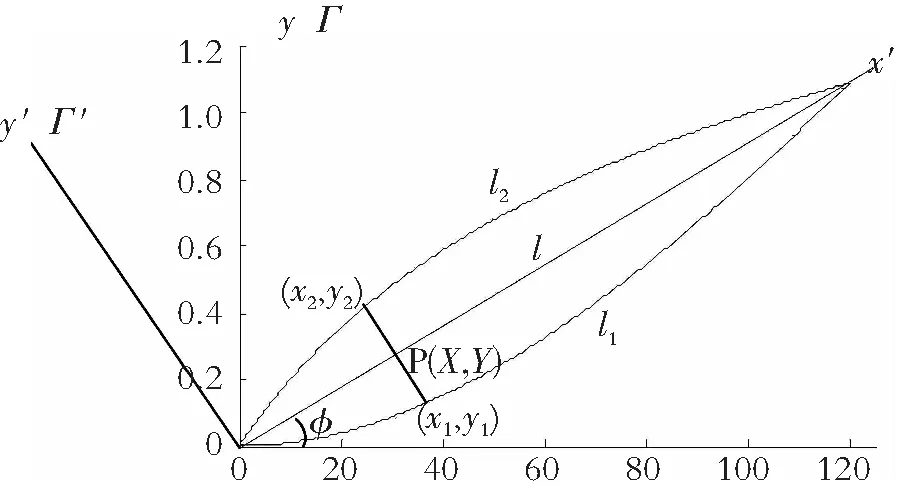
图3 坐标系的旋转及回路曲线的转换Fig.3 Rotation of the coordinate system and the transformation of the loop curve

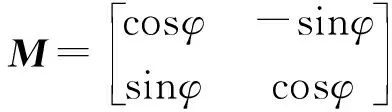
两坐标系变量之间的关系为
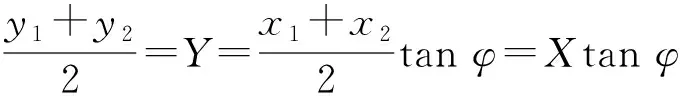
(1)
由式(1),如能用Y与X的线性关系来表示控制系统的位移与电压,则会使控制系统非常简单。虽然X、Y并非实际上压电作动器上的电压和位移值,因为点(X,Y)不在主回路曲线之上,但x1和x2是回路上两点对应的电压值,可以很容易地获得和控制。同时,注意到(x1,y1)与(x2,y2)两点分别位于顺调与逆调曲线上,且相对于l轴对称。如果采用两个PZT位移作动器,并使它们也分别位于顺调与逆调曲线上且有电压x1和x2,则它们的电压之和为2X,此时的位移输出之和就是2Y。由此可实现X、Y之间的线性关系,通过调节X来得到相应的Y。相应的x1和x2可由式(2)计算:
(2)
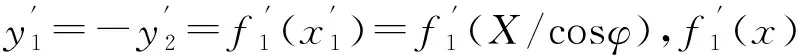
2 位移控制系统的结构与实现
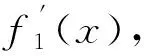

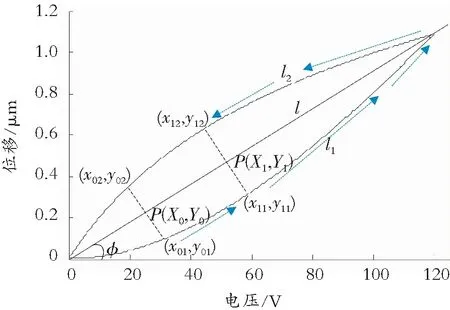
图4 对称轴上点的线性移动;箭头线段指示从(x01,y01)到(x12,y12)的驱动方式Fig.4 Linear movement of points on the axis of symmetry;the arrow lines indicating the way of driving from (x01,y01) to (x12,y12)
综上所述,实现线性位移控制系统的主要步骤如下:
① 选择一对具有相同迟滞行为的压电作动器;
② 根据测量范围及对称性要求,确定出一个主回路;
③ 由曲线拟合或其它方法,测定所选回路的曲线函数;
④ 根据给定位移Y,由公式(1)和(2)计算出作动器电压x1与x2;
⑤ 依据当前状态参量(电压或位移),判断压电作动器谁在顺调曲线和谁在逆调曲线,并分别赋值x2与x1。
⑥ 采用同时驱动或先后驱动的方式,沿逆时针方向,调节作动器电压使其达到给定值x1与x2;
⑦ 对于新的位移或位置,重复步骤④—步骤⑥。
由于采用两块压电作动器协同调节,在一个固定的回路上以单循环方式驱动,有效避免了压电迟滞带来的非线性影响,其输入电压与输出位移的线性关系得到保证,大大地简化了控制系统的计算量且勿需额外的系统装置或部件。
3 实验结果及误差补偿
为验证系统的有效性,设计了一个简单的实验来进行测试,如图5所示。
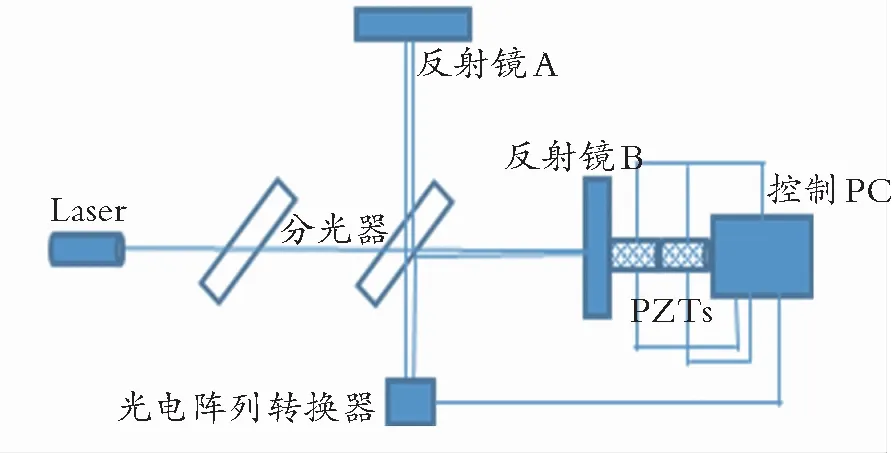
图5 实验装置结构示意图Fig.5 Schematic diagram of the experimental setup
实验装置包括Michelson干涉仪,光电转换阵列,PZT位移作动器和一台用作控制的电脑。可移动反射镜B可通过PZT作动器驱动,反射镜A固定。二个性能一致的PZT位移作动器首尾相连,每一个可通过电脑独立控制。电脑通过数-模转换器和放大器与作动器相连。带有移动镜B位移信息的干涉条纹通过光电阵列后输入电脑,从而获知其位移量的大小。实验系统的位移测量量程为10 μm,精度则为1 nm。
为保证二个压电作动器的迟滞行为一致,可在同一型号或同一批次产器中选择,并进行测试;同时,迟滞主回路的最大电压值或最大位移值要小于饱和点相应的值,且尽可能使主回路的顺调曲线与逆调曲线具备轴对称性。通过实验测试并采用曲线拟合方法可得到压电作动器及主回路基本参数,如表1所示。

表1 作动器与主回路参数Table 1 Paraments of actuator and main loop
顺调曲线段相应的函数关系y=f(x)可表示为
y=0.5×10-4x+1.02×10-4x2-2.25×10-7x3+R(x)
(3)
其中余项|R(x)|<0.001 μm。
通过坐标系旋转φ=32.102°后可得y=f′(x),可表示为
y=-9.0×10-3x+1.029×10-4x2-2.080 3×10-7x3
(4)
实际的逆调曲线与根据轴对称假定得到的逆调曲线(即f(x))最大误差为0.05 μm,平均误差为0。
依据文献(23)的结果,采用中心对称模型时得到的最大误差小于0.001 μm,因此基于中心对称性得到的逆调曲线实际上可看成是真实的曲线。设中心对称回路的中心坐标为O(Xo,Yo),则逆调曲线函数为y=2Yo-f(2Xo-x),在位置P(X,Y)处由轴对称模型产生的误差为
Δ=y2-y=2Y-f(x1)-2Yo+f(2Xo-x2)
(5)
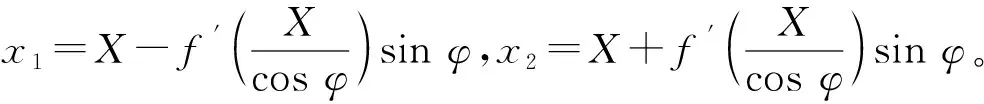
注意到2Xo-x2=2(Xo-X)+x1,所以Δ又可表示为
Δ=2(Y-Yo)+f[2(Xo-X)+x1]-f(x1)
(6)
容易看出:当Y=Yo,Y=2Yo,Y=0,有Δ=0,也就是在回路底点、中点及顶点处是不存在误差,这一特性由实测数据得到验证。应用拉格朗日中值定理把Δ重写为
2(Xo-X)(tanθ-tanφ)

Δ=2(Xo-X)(tanθ-tanφ)≈
2(Xo-X)sec2δ×δ≈
2(Xo-X)δ
为了补偿误差,需要把逆调曲线上由计算得出的电压值x2进行修正调节。设使误差最小时的电压值为x,且考虑到x应当在x2附近,可设x=x2+ε,ε是一小数。在式(5)中把x2替换成x并令Δ=0可得
f(2Xo-x2-ε)=2Yo-2Y+f(x1)
再应用拉格朗日中值定理,得到
当需要对误差进行修正时,系统的调节秩序只需在表1的基础上略加修改,加入对ε的计算并用x2+ε代替原来的x2即可,这里不再给出具体步骤。
因为两个作动器可以独立控制调节,最简单的办法是采用顺序调节的方法,也就是先把其中一个调节到新位置后再调节第二个。假设需要将系统位移输出按图7中P1,P2,P3与P4的次序进行调节,则其中一个作动器的位置将分别位于图8中1,2,3,4处;电压调节过程如图8所示,与图8中4点对应的电压值则是图9中1,2,3,4处的值。

图7 对称轴l上各点与作动器在回路上的位置变化Fig.7 Positions along the axis l and the sequential points on the loop paths
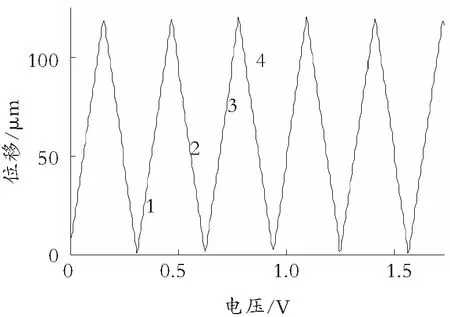
图8 图7中P1-P4各位置相对应的作动器输入电压大小(1-4处)Fig.8 Inputting voltages through the corresponding actuator to P1-P4 in Fig.7(at 1-4)

图9 误差随位移大小的变化(带误差修正的为实线)Fig.9 Variation of error with position(solid line with error correction)
图9是系统输出位移与干涉仪位移差值的对比,此处干涉仪由于误差很小,可看成是近似的真实值。图中的水平虚线为干涉仪参考误差,而曲线反映了系统误差随输出位移大小变化的情况。从图中可以看到,最大输出位移为2×1.086=2.172 μm,此时电压最大值为120 V。产生误差的主要根源是模型假设的对称性与实际迟滞曲线的差异。如果不考虑其他因素,如老化、蠕变、温度等的影响,在不进行误差修正时,最大位移误差为0.039 μm,是最大位移量的1.76%,同时平均误差为0.001 6 μm,是最大位移的0.074%。在误差补偿后,最大误差及平均误差分别减小至0.015 μm及0.001 μm。图10是系统位移输出的一半(即两个作动器输出平均值)与主回路对称轴的比较,在误差修正的条件下,作动器输出位移与两个作动器输入电压之和呈线性关系,两者之间的差异几乎可以忽略。从实验的结果来看,本文所提出的基于轴对称迟滞模型相比于其他已知模型,如PI模型、电荷控制模型、反函数模型或闭环控制类模型,其优点是明显的。除了误差较小、容易实现、结构简单、计算量小且易于电压控制等优势外,其最大的优点是可实现输入与输出之间的线性关系而勿需额外的计算与设备;不足之处在于要应用两块性能一致的作动器,且需要选择一个尽可能符合轴对称要求的主循环回路。
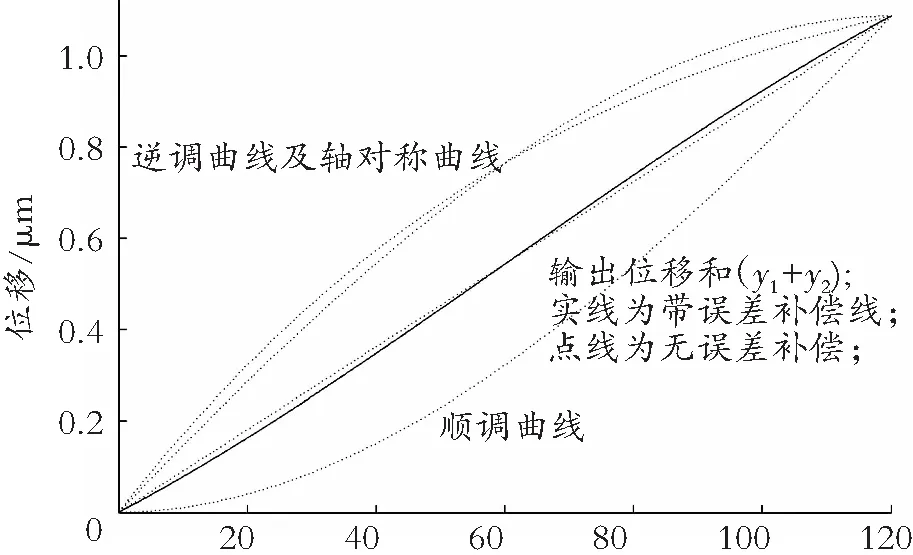
图10 输出位移与输入电压之间的线性关系Fig.10 Linear relationship between output displacement and input voltage
4 结束语
提出了一种利用压电迟滞回线的轴对称性来改善由于迟滞效应产生的非线性。首先在满足位移量程与对称性要求的条件下,采用了单一的主回路以达到简化控制系统并提高精度的目的。文中对主回路顺调曲线与逆调曲线之间的对称性进行了研究,并把这种对称性应用于线性位移系统控制模型的建立。依据这种对称性,可在系统位移输出与电压输入之间建立一种简单的线性关系;而实现这种线性关系的关键是采用两个位移作动器沿主回路进行逆时针方向驱动,这样可避免其他不相关的次级回路的出现,并保证它们在最终位移输出时分别处于回路的两个对称点上。实验结果证明了所设想的线性位移模型的有效性和可实现性。文中还针对模型特点,对误差进行了讨论。根据实验结果,位移输出精度可达到1 nm量级,最大误差15 nm,平均误差约0 nm。与其他文献中报道的迟滞补偿模型相比,模型具备结构简单、计算量小、易于实现、输入与输出为线性关系等优点;不足之处是对迟滞回路对称性的依赖。下一步工作可针对其他压电非线性行为,如温度、蠕动等进行研究,同时考虑如何优化地确定用于驱动作动器的主回路,以进一步改善模型。
