基于相同稀疏模式的稀疏主成分分析算法

邵剑飞，浦 蓉，黄 伟，季建杰，郭 鹏

（1.昆明理工大学信息工程与自动化学院，昆明 650500；2.云南电网有限责任公司红河供电局，红河 661100）

引 言

主成分分析（Principal component analysis，PCA）是数据分析中一种流行的特征提取和降维技术［1-2］，被广泛应用于图像和视频分类［3］、图像去噪［4］以及面部识别［5］等应用数据分析［6］中。但是，传统PCA的主成分是原始变量的线性组合并且载荷通常为非零，因此稠密的主载荷向量导致主成分缺乏可解释性。而稀疏主成分分析方法是计算具有少量非零项的主载荷向量实现特征选择，同时使模型具备更好的可解释性［7］。Zou等［8］提出了稀疏主成分分析算法（Sparse principal component analysis，SPCA）。SPCA算法首先证明PCA可以表述为回归型优化问题，然后通过对回归系数施加套索（弹性网）约束来获得稀疏载荷，但该算法不能保证在所有主载荷向量上都保留稀疏模式，即非零变量的位置在不同的主载荷向量上是不同的。Jenatton等［9］提出了一种结构化且稀疏的主成分分析算法（Structured and sparse principal component analysis，SSPCA）。SSPCA算法定义了范数的组与由此产生的非零模式之间的关系，提供了从组到模式来回的向前和向后算法，设计适合以非零模式表示的特定先验知识的规范。该算法对主载荷向量的稀疏模式施加约束，但是由于SSPCA算法需要进行通用优化，因此除非事先提供了正确的模式，否则SSPCA算法并不总是能够正确估计所有分量的稀疏模式。

在以上研究的基础上，本文提出了一种自适应稀疏PCA算法（Adaptive sparse principal component analysis，ASPCA）。该算法通过使用组套索模型，在载荷向量上施加块稀疏约束找到最小化的稀疏载荷矩阵和正交矩阵，得出自适应稀疏PCA公式；对稀疏矩阵的不同列使用不同的调整参数以获得自适应惩罚，使得稀疏矩阵不同列具有不同的收缩量，从而在主载荷向量上保留稀疏模式；采用块坐标下降法对自适应稀疏PCA公式进行两阶段优化，找到稀疏载荷矩阵和正交矩阵，提高特征选择的能力。仿真结果表明，相比SPCA算法和SSPCA算法，ASPCA算法的降维效果显著，且能提取更有价值的特征，有力的提高了分类模型的平均分类准确率。

1 稀疏主成分分析

令X表 示 秩 为q≤min(n，p)的n×p数 据 矩 阵，其 中n为 数 据 样 本 数，p为 变 量 数。对 于i=1，…，n，X的行表示为xirow，假定其以0为中心且为p×p的正定矩阵，可以分解为

式中：λi表示Σ的第i个最大特征值；vi=(vi1，…，vip)T为Σ关联的特征向量。PCA通过将原始变量替换为主成分Xvk，k=1，…，q的q个线性组合，从而将数据的维数从p减少到q，通过最大化其方差获得主载荷向量，即

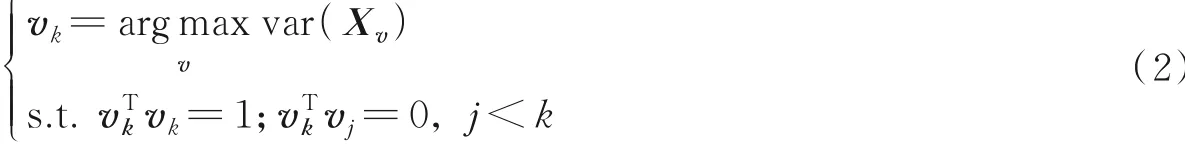
式中：vk为第k个主载荷向量；Xvk的投影为第k个主成分；var(·)表示随机变量的方差。当使用q≪p的分量来解释数据的大部分差异，进而解释基础数据结构时，PCA最为理想。协方差矩阵Σ从数据上进行估计，载荷向量从估计矩阵Σ̂的特征值-特征向量分解进行估计。

基于投影框架导出PCA的替代公式，其中主载荷矩阵（V定义为包含主要载荷向量的矩阵）通过最小二乘法估计

式中V=(v1，…，vq)为p×q主载荷矩阵。

使用X的奇异值分解（Singular value decomposition，SVD）计算PCA为

式中：Z≜UD的列是主成分；而V的列是相应的载荷向量。矩阵D是有序奇异值d1≥d2≥…≥dq＞0的q×q对角矩阵，并且U和V的列正交，因此UTU=VTV=Iq。式（4）的SVD也提供了与X最接近的秩q矩阵近似，其中X和秩q近似矩阵的接近度用F-范数的平方来表示，定义为

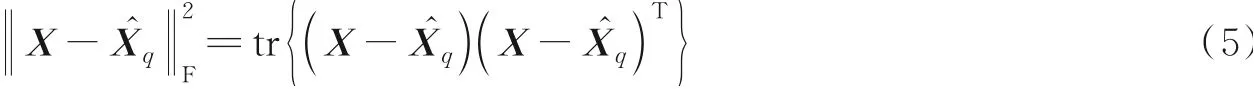
这个秩q近似也对应于q个秩1近似，即

式中：b=d1v，向量u和v分别为n×1和p×1的矩阵，且本文用式（6）描述PCA的稀疏性。在b上添加L1-范数作为稀疏正则约束获得稀疏载荷向量，表示为

式中bi为b的分量。在式（7）中，稀疏惩罚对向量b的各个元素施加约束，这种约束b元素的方式导致了在不同成分之间稀疏模式变化的问题。但现有的稀疏PCA方法均不能保证在所有主载荷向量上都保持稀疏模式，也就是非零变量的位置在不同的主载荷向量上是不同的。

2 自适应稀疏主成分分析算法

2.1 自适应稀疏PCA公式

为了在所有主载荷向量上保留稀疏模式，本文采用组套索模型惩罚分组变量［10-12］。通过在载荷向量上施加块稀疏约束并找到最小化的向量U和BT的列向量，得出自适应稀疏PCA方法的公式为

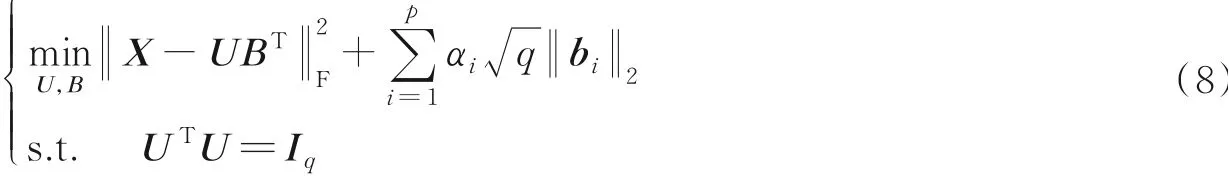
传统的稀疏PCA是式（8）描述的通用特例，但是如果需要一个以上的主成分来充分描述数据，则本文提出的自适应稀疏PCA方法具有保留相关载荷向量间稀疏模式的优点。式（8）使用L2，1-范数进行双重正则化，先求矩阵BT第i列向量bi的L2范数，再将结果求L1范数，同时实现收缩和选择，可以使一些大小为q的系数块恰好为0。代价函数式（8）通过对BT的不同列使用不同的调整参数αi获得自适应惩罚，从而保证BT的不同列出现不同程度的收缩。对于一组αi，式（8）的优化在某种程度上是唯一的，以下命题讨论了式（8）解的唯一性。

命题2从代价函数式（8）获得的具有非零L2-范数的BT列是唯一确定的。

2.2 调整参数计算

在式（8）中，自适应调整参数为惩罚向量bi(i=1，…，p)提供灵活的惩罚，保证不同的bi向量产生不同的收缩量。直观地说，必须对L2范数为零的向量采用较大的收缩量，而对于L2范数非零的向量应使用相对较小的收缩量。在实际中，对p个调整参数的选择进行贪婪搜索需要大量的计算。为了减少计算量，提高效率，设αi为

2.3 代价函数优化

代价函数式（8）是双凸结构，对于固定U或B都是凸的，采用块坐标下降法［13］对其进行两阶段优化。第1阶段固定U求解B对式（8）进行优化，第2阶段固定B求解U优化式（8）。优化到最后，B表示稀疏载荷矩阵，U将是一个完全正交的矩阵。

第1阶段对应于

式（11）的第1项可以改写为

式中xi为X的第i列，其为n×1。

关于bi的次梯度方程为

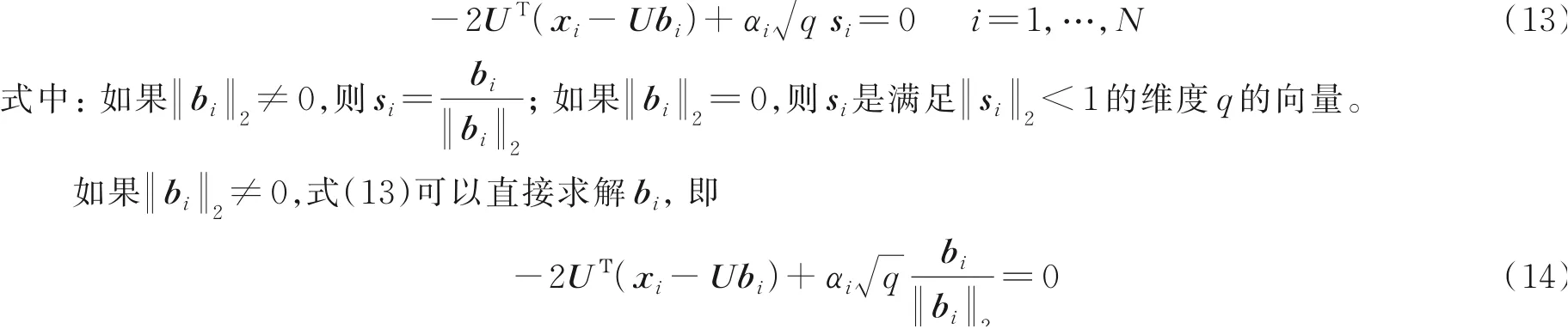
的解为

对式（15）两边同时取L2范数进行求解

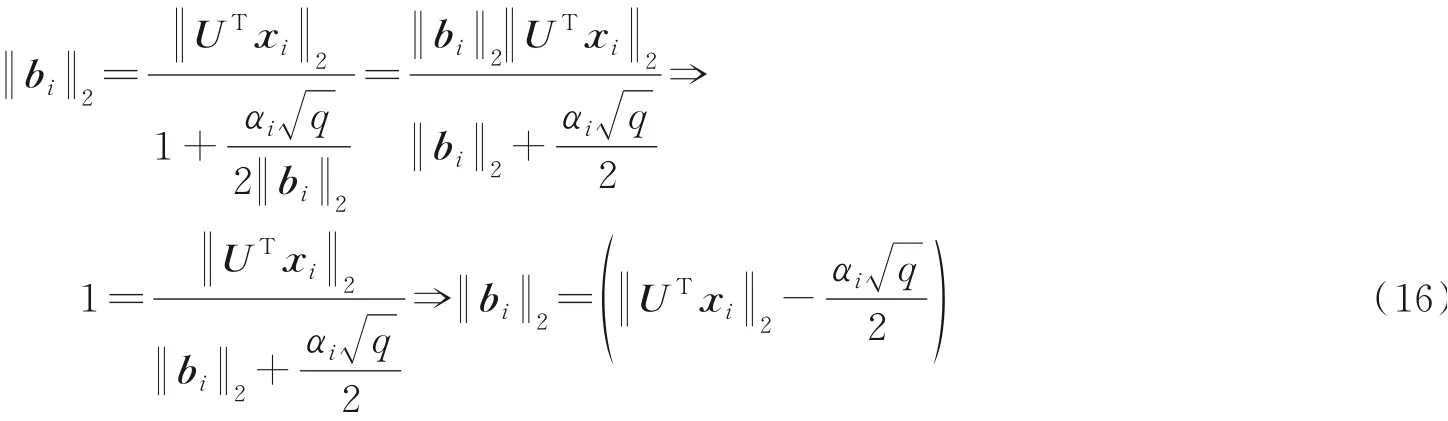
将此解代入式（15），得

解si为

式（8）中优化的第2阶段定义为

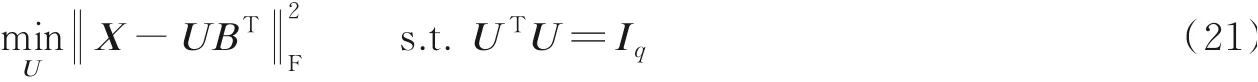
这是一个正交的Procrustes问题［14］。解为是从的SVD得到的，其中

2.4 算法描述

根据命题1和命题2对自适应稀疏PCA公式解的说明以及调整参数的计算公式，利用块坐标下降法两阶段优化的结果，ASPCA算法伪代码如算法1所示。

算法1自适应稀疏PCA算法（ASPCA）

输入数据矩阵X，稀疏主成分的数量q，调整参数α，阈值ε。

输出稀疏载荷矩阵B，正交矩阵U。

（1）B作为第1个q右奇异向量乘以X的第1个q奇异值；

（2）使用式（10）计算调整参数αij的向量；

（3）使用式（20）更新BT及其每列的稀疏性；

（4）Forj=1～p

通过算法1可知，将数据矩阵、稀疏主成分的数量、调整参数以及阈值作为输入端，首先计算出调整参数，然后迭代计算得出矩阵BT和U，最后得到稀疏载荷矩阵B。ASPCA算法使用块坐标下降法几次迭代后达到合理的收敛容限，因此该算法是稳定并保证收敛的。

2.5 算法复杂度分析

对于ASPCA算法，复杂性主要取决于迭代次数。对于非迭代部分，计算调整参数所需的SVD的计算复杂度为O(np2)。更新U，SVD的计算复杂度为O(qn2)，矩阵乘积计算复杂度为O(npq)。因此，矩阵U的计算复杂度由SVD决定。更新B，UTxi的计算复杂度为O(nq)，使用式（20）计算bi的计算复杂度为O(nqp)。

3 仿真分析

3.1 数据集

与其他类似算法的仿真研究一致，本文将ASPCA算法应用到3种MNIST数据条件的数字分类任务中来评估算法降维的有效性。MNIST数据库［15］的3个不同背景条件为：（1）无背景；（2）背景中有均匀的随机噪声；（3）背景中随机出现无法识别的图像。本文使用大小为28像素×28像素、p=784、n=1 000的灰度矢量化图像。图像被矢量化和叠加，形成n×p数据矩阵X，其中p为每个图像中变量（即像素）的数量。本文主要研究在主成分上保留稀疏模式的有效性，降维后执行标准的最近邻分类，只关注PCA降维的效果。使用n=1 000个训练样本计算主载荷矩阵，降维后这些样本用于训练分类器。

3.2 准确率分析

（1）无背景时的准确率分析

如图1所示，在无背景情况下，随着主成分数量的增加，SPCA算法、SSPCA算法和ASPCA算法的平均分类准确率均逐渐提高且相差不大。图中所示的准确率是测试数据的10个不相交子集的平均值。当主成分数量小于50个时，ASPCA算法和SPCA算法的平均分类准确率一致且高于SSPCA算法，因为没有关于稀疏模式结构的先验信息，SSPCA算法需要花时间确定正确模式。也就是当主成分数量小于50个时，ASPCA算法和SPCA算法的降维性能优于SSPCA算法。当主成分数量大于50个后，3种算法的平均分类准确率一致，达到了88%，即在无背景情况下，随着主成分数量的增加，SPCA算法、SSPCA算法和ASPCA算法降维效果逐渐接近且相差不大。

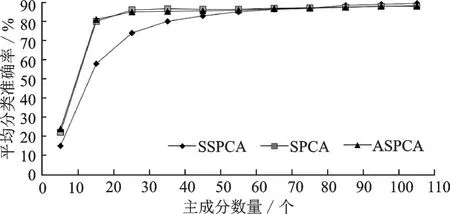
图1 无背景时准确率随主成分数量的变化Fig.1 Variation of average classification accuracy with the number of principal components in no background

（2）背景中有均匀随机噪声的准确率分析

如图2所示，当背景中有均匀的随机噪声时，随着主成分数量的增加，ASPCA算法的平均分类准确率优于SPCA算法和SSPCA算法且稳定。在主载荷上引入稀疏度可以帮助选择原始空间中的重要特征，但当提取的主载荷数量增多时，SPCA算法需要分别处理主成分。因此随着主成分数量的增加，SSPCA算法和ASPCA算法的降维效果优于SPCA算法。当主成分数量大于等于90时，SSPCA算法和ASPCA算法的平均分类准确率逐渐相近，达到75.3%，降维性能接近一致。

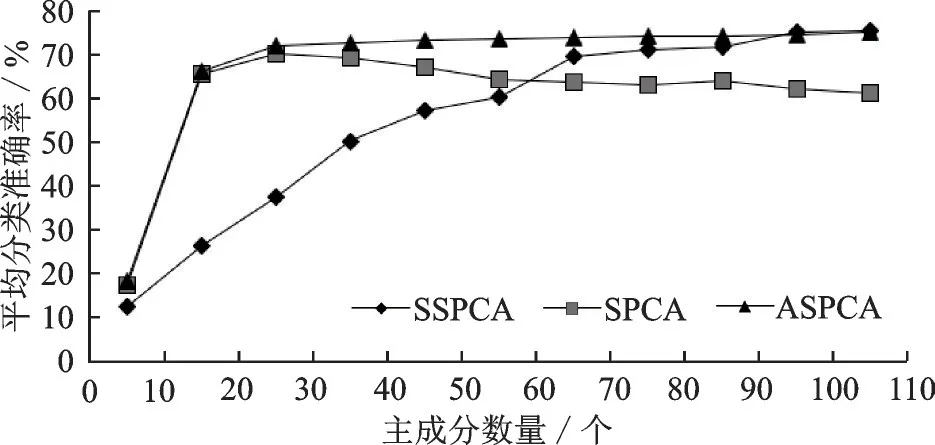
图2 背景中有随机噪声时准确率随主成分数量的变化Fig.2 Variation of average classification accuracy with the number of principal components in the background with random noise

（3）背景中随机出现无法识别图像的准确率分析

如图3所示，在背景中随机出现无法识别图像的情况下，随着主成分数量的增多，ASPCA算法、SPCA算法和SSPCA算法的平均分类准确率逐渐提高。因为ASPCA算法能够从数字数据的固有可变性中提取更多信息，从而不会受到背景噪声的干扰，能用更少的主成分实现更高的分类精度。对比SPCA算法和SSPCA算法，ASPCA算法的平均分类准确率较高，即在背景中随机出现无法识别图像的情况下，ASPCA算法的降维效果优于SPCA算法和SSPCA算法。

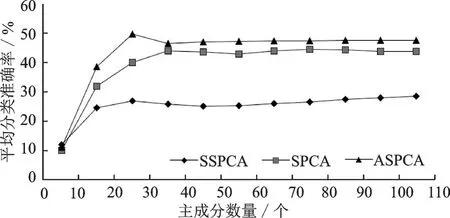
图3 背景中随机出现无法识别图像时准确率随主成分数量的变化Fig.3 Variation of average classification accuracy with the number of principal components in the background appearing unrecognizable images randomly

可见，在对3种MNIST数据条件的数字进行分类的过程中，ASPCA算法的降维效果优于SPCA算法和SSPCA算法，尤其是在存在噪声情况下提取具有相同稀疏性模式的载荷向量是重要的。

4 结束语

为了解决主载荷稠密的问题，本文提出了一种ASPCA算法。通过在载荷向量上施加块稀疏约束得出ASPCA公式，对稀疏矩阵的不同列使用不同的调整参数获得自适应惩罚，使主载荷向量在所有主成分上都具有相同的稀疏性模式；然后，通过块坐标下降法进行优化找到最小化的稀疏载荷矩阵和正交矩阵，实现降维的最优化。仿真结果表明，ASPCA算法的降维性能更优，能提取更有价值的特征，从而有力地提高了分类模型的准确率。