基于Adams离散和Newmark-β法求解分数阶van der Pol系统*

姜宏杰，刘祚秋，吕中荣，刘广

中山大学航空航天学院，广东 广州 510006

与整数阶导数相比，分数阶导数具有方程简洁和参数意义明确等优点，通过分数阶微分系统描述的现象更加接近于真实的自然现象，因此分数阶导数在非线性振动［1］、控制理论［2］、参数识别［3-5］等领域有广泛的应用。vdP（van der Pol）系统［6］最初是荷兰工程师Balthazar van der Pol在研究三极管的振荡效应中提出的。作为一种典型的自激系统，其在不同的参数条件下能够展现出多种丰富的动力学现象，因此基于vdP系统的研究产生了众多的学术成果。

目前，学者们也针对含分数阶导数的vdP 系统进行了研究。Barbosa 等［7］通过分析分数阶vdP 系统的相图、分岔图以及借谱分析等，较为详细地研究了分数阶vdP 振动系统在时域和频域的动力学行为；Tavazoei 研究了分数阶vdP 系统的极限环与初始条件的关系，并给出了存在极限环的解析判据；Chen 等［8］用相轨迹图和庞加莱映射研究了分数阶vdP系统的混沌动力学行为，发现分数阶阶次会直接导致系统进入混沌状态。毛北行等［9］基于Lyapunov稳定性理论给出了分数阶Duffling-van der Pol系统混沌同步问题的两个充分性条件。韦鹏等［10］以含分数阶vdP 系统为对象，研究了其超谐共振时的动力学特性，得到了超谐共振周期响应的稳定性判断准则，同时提出等效非线性阻尼和非线性稳定性条件参数的概念。

上述是从定性角度来描述和分析分数阶vdP系统的各种性质，定量的研究则需要获取系统较为精确的数值解或解析/半解析解［11-12］。和整数阶非线性系统不同的是，分数阶微分算子的引入使得系统的解析/半解析解的求解难度急剧上升，相关的成果非常少。所以，现阶段我们更加关注分数阶vdP 系统的数值求解。对于整数阶非线性系统，数值计算法包括有限差分法［13］、Runge-Kutta 法［14］、精细积分法［15］、预估校正法［16］等。对于分数阶微分系统，即便是数值方法也尚在发展当中。

Newmark-β法是一种非常成熟的数值方法，它是基于ti时刻的运动状态ui、u˙i、u¨i，然后进一步计算ti+1时刻状态，逐步获得结构动力响应的逐步积分法。Newmark-β法通过简单的参数设置便可以无条件稳定，且编程简单易于实现，这些特点使其在整数阶微分系统中得到了广泛应用。在本文中，我们将基于Adams离散，提出一种针对Caputo分数阶导数的离散格式，然后进一步基于Newmark-β法构造出完整的逐步迭代格式，最后通过Newton-Raphson迭代［17］来进一步求得分数阶vdP系统的响应。

1 基于Adams离散和Newmark-β法的迭代格式

1.1 对分数阶算子Dαx进行Adams离散

对于如下形式的分数阶vdP方程［18］

其中μ为阻尼系数，Dαx表示分数阶微分算子，α为对应的分数阶阶次。分数阶导数Dαx通常有Riemann-Liouvill 定义、Caputo 定义和Grünwald-Letnikov 定义［19-21］。本文中，分数阶算子Dαx采用Caputo 定义［22］。当分数阶次0 ＜α＜1时，有［23］

其中求积系数di，n为

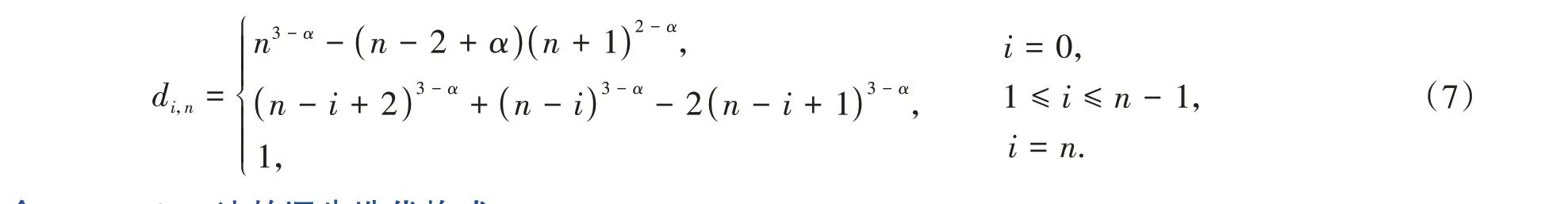
1.2 结合Newmark-β法的逐步迭代格式

当分数阶阶次α= 0.5时，分数阶vdP系统可以被完整地表示为

式中β和γ为Newmark-β法的控制参数，Δt=tn-tn-1为时间步长。进一步，将方程（10）中的状态变量代入到方程（9）中，可以得到系统（8）的完整迭代格式

可以看出，系数A、B、C、D是通过β、γ、tn、α等表示的常数，则方程（12）是关于tn时刻未知位移xn的非线性代数方程。

1.3 通过Newton-Raphson迭代法求解位移方程

方程（12）可以通过Newton-Raphson 迭代法来求解。Newton-Raphson 迭代本质上是将非线性方程f(x) = 0 进行泰勒展开，并保留一阶项得到线性化方程来寻求方程f(x) = 0 的根。对于方程（12），有f(xn) =Axn+Bxn2+Cxn3+D= 0，则f(xn)的泰勒展开为

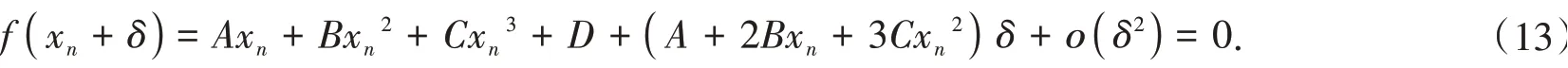
对于足够小的δ，忽略二阶及以上的项，可得

需要注意的是，通过Newton-Raphson 迭代求解xn，需要选取一个合适的初值［26］。通常选取上一时刻tn-1的位移xn-1作为下一时刻的迭代初值。获得位移xn后，将其代入方程（10），得到系统的速度和加速度。自此，系统在tn时刻所有的状态变量全部获得。重复多次，就可获得分数阶vdP 系统完整的时程响应。

2 数值算例

2.1 0 < α < 1的分数阶vdP系统

首先假定分数阶阶次α= 0.5，即以系统（8）为例，取参数μ= 0.8.Newmark-β法中的参数取值为β=0.25、γ= 0.5. 由初始条件x0= 0，x˙0= 1可以计算出x¨0，进一步计算获得t1的系数A、B、C和D，然后逐步获得系统的数值响应。图1为α= 0.5时系统（8）的时程响应，图2是对应的相图。

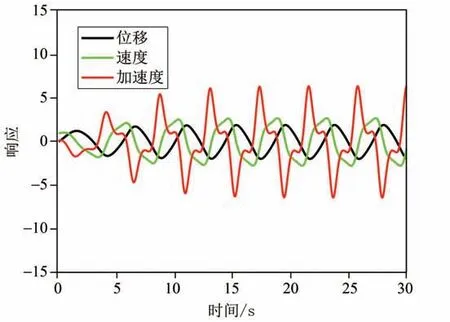
图1 系统（8）的时程响应Fig.1 The time histories of system(8)

图2 系统（8）的相图Fig.2 Phase diagram of system(8)

由图1可以看出，在最初的15 s内，系统出现了瞬态响应，但是逐渐地系统进入稳态响应，对应的相图则出现了稳定的极限环。这说明本文所提的数值方法不会出现失稳现象，可以稳定获得系统的数值响应。当分数阶阶次α→1时，系统（8）将会退化为对应的整数阶vdP系统，即

通过整数阶的数值方法验证本文所提方法的有效性。当α= 1 时，四阶Runge-Kutta（RK）法和本文所提方法获得的时程曲线和相图，如图3所示。从图中可以看出，无论是时程曲线还是相图，两种方法获取的结果吻合很好。这证明本文的方法对于整数阶微分系统仍旧是有效的。

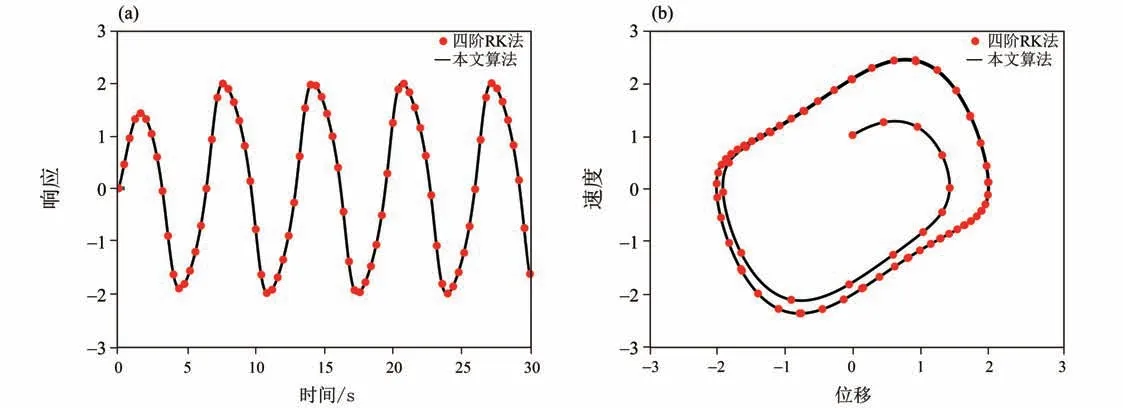
图3 α = 1时，四阶RK法和本文算法的时程曲线（a）和相图（b）Fig.3 The time histories(a)and phase(b)obtained by fourth-order RK method and the algorithm of this paper when α = 1

2.2 1 < α < 2的分数阶vdP系统

不失一般性，可以假定系统（1）中的分数阶阶次α= 1.5，μ= 0.8. 则系统（1）有如下形式

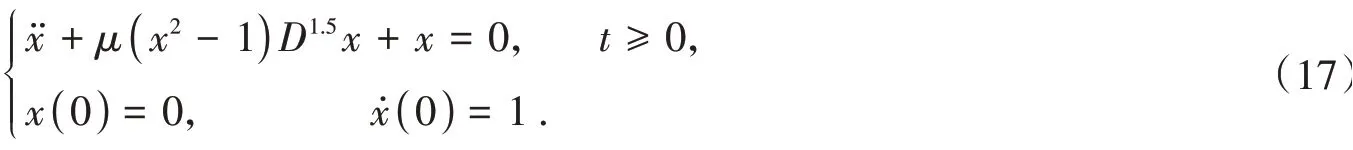
与α= 0.5的讨论类似，结合Adams离散和Newmark-β法，可以得到系统（17）的逐步迭代格式

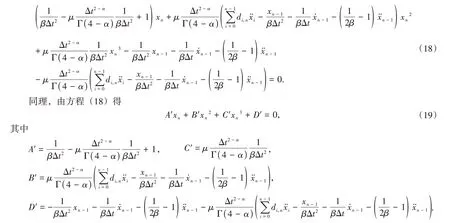
与上一个算例类似，在tn时刻系数A′，B′，C′和D′也是β、γ、tn、α表示的常数，则方程（19）是关于未知位移xn的非线性代数方程。将xn代入方程（10）得到系统的速度与加速度。

本算例中，Newmark-β法中的参数取值与2.1节相同，时间步长取Δt= 0.1.α= 1.5时，系统（17）的时程响应和相图，如图4和图5所示。

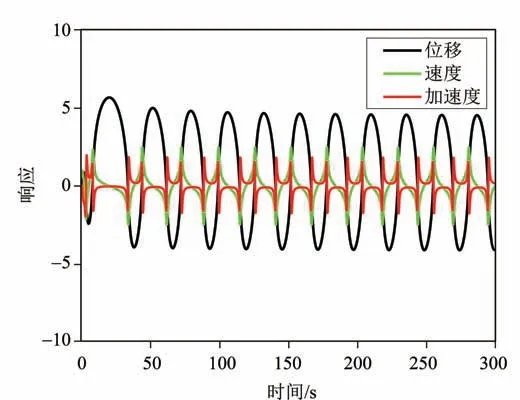
图4 系统（17）的时程曲线Fig.4 The time histories of system(17)

图5 系统（17）的相图Fig.5 Phase diagram of system(17)

从图4所示的时间历程可以看出，由于初始状态的影响，系统出现了瞬态响应，经过一段时间后才进入稳态。且，由于本算例中α= 1.5，其时程曲线与α= 0.5时明显不同，相图也有明显的区别。此外，α=1.5对应的响应频率比α= 0.5时要小得多。同样，当分数阶阶次α→2时，系统（17）也会退化为对应的整数阶vdP系统。

α= 2时，四阶RK 法和本文所提方法获得的时程曲线和相图，如图6所示。从图6可以看到，本文方法和四阶RK 法的结果吻合非常好。对比图4和图6（a），可以发现α= 1.5和α= 2时vdP 系统的响应完全不同；对于α= 1.5 的分数阶vdP 系统，系统的速度和加速度都存在明显的尖峰。对比图5 和图6（b），可以发现α= 1.5对应的相图更接近于一个方形，而α= 2时的相图则是一个椭圆。同样的，本文所提的离散格式和数值方法也可以很好地求解1 ＜α＜2的分数阶vdP系统。

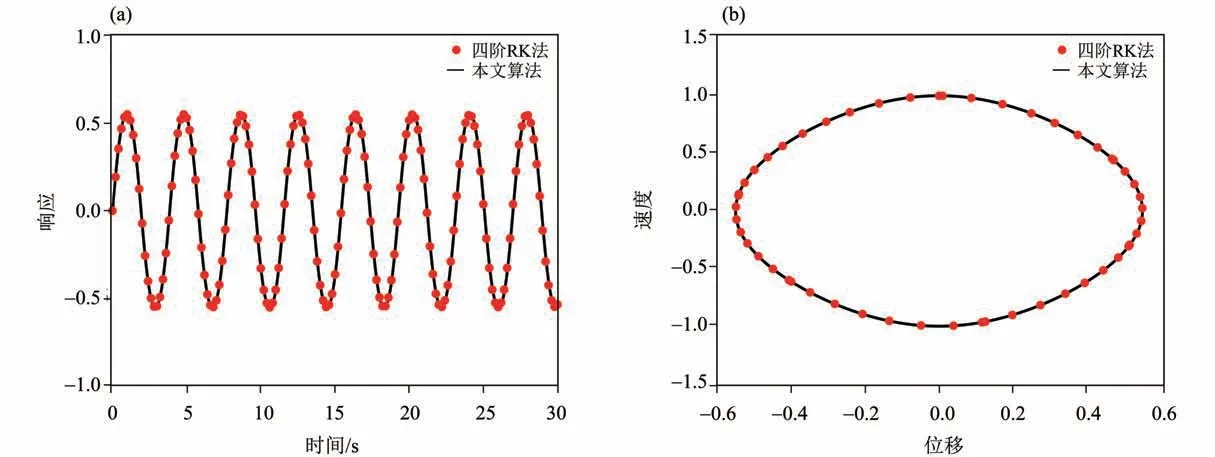
图6 α = 2时，四阶RK法和本文算法的时程曲线（a）和相图（b）Fig.6 The time histories and phase obtained by fourth-order RK method （a）and the algorithm of this paper （b）when α = 2

3 结 论

本文基于Adams离散和Newmark-β法，提出了一种求解分数阶van der Pol系统的逐步迭代格式，并分别讨论了0 ＜α＜1 和1 ＜α＜2 对应的vdP 系统的数值求解。结果表明，本文所提方法可以稳定获得分数阶微分系统的数值解。此外，我们还讨论了α→1和α→2时，即分数阶vdP 系统退化为整数阶vdP 系统时的情形。结果表明，本文所提算法和四阶RK法获得的结果吻合非常好。原则上，本文所提的迭代格式适用于其他类型的分数阶微分系统。