不同车辆模型作用下混凝土简支T梁桥的动态称重研究

2022-10-13邓洁松付壮金孙治超

黑龙江工业学院学报(综合版) 2022年9期

王芳，邓洁松，付壮金，孙治超

(宿州学院资源与土木工程学院，安徽宿州 234000)

我国桥梁上行驶车辆的重量、数量在随着社会经济的不断发展而不断增加，普遍存在的超载现象导致诸多在役桥梁未达到设计寿命就提前结束服役[1-3]。超载运输不仅严重影响了国家公路交通运输中收费秩序的正常运行，还可能对公路桥梁造成不可逆的损伤，导致桥梁承载能力退化、运营寿命缩短，甚至直接垮塌[4]。因此，发展快速有效的车辆荷载识别技术、提高超载车辆监管水平，对保证我国桥梁运营安全具有重要的意义。

桥梁上移动荷载识别实质上为动力学反问题，即已知桥梁响应(如应力等)求解车辆信息(如重量、速度等)。桥梁动态称重(Bridge Weigh-in-motion，简称BWIM)系统将既有桥梁当作一个固定的称重磅秤站，通过传感器获取桥上通行车辆作用下桥梁的实时响应，结合预先标定的桥梁影响线来识别车辆速度、车轴、车辆轴重和总重等信息[5]。

Moses于1979年第一次提出BWIM的概念和算法，并于1992年与Snyder申请了该项专利[6]。近年来国内外有关专家和部门对桥梁动态称重系统进行了一系列的研究，国外桥梁动态系统已经有具体的实际应用。我国近年来在桥梁动态称重领域已经开展了一系列的研究，为推动BWIM桥梁动态称重系统的实际推广作出了很多重要的工作。耿少波等人采用两组中小跨径试验桥为对象，研究了BWIM系统中影响线方法对车辆荷载信息识别精度的影响[7]。任伟新等[8]对BWIM技术的发展历史和研究现状进行了总结，并探讨了桥梁动态称重系统的发展前景。王宁波等[9]通过对BWIM系统在不同桥型上对比研究发现，部分梁板桥、正交异性板桥及框架桥对该技术的适用效果较好，箱梁桥上的识别效果则不佳。目前移动荷载识别的已向复杂荷载以及多元化发展，同时相继发展了多种衍生算法，但荷载识别理论基础仍是Moses算法[10]。

本文基于Moses算法针对典型混凝土简支T梁桥在两种不同车辆模型作用下的识别效果展开研究。通过数值模拟计算分析了三轴车和五轴车两种车辆模型在混凝土简支T梁桥上的识别效果，分别识别了车辆的速度、轴距、车辆轴重和总重等信息，并对比分析了不同路面不平整度、车辆行驶速度等因素对两种车辆模型识别精度的影响。

1 桥梁动态称重算法——Moses算法

经典的Moses算法首先通过已知信息的车辆去标定桥梁得到实际的桥梁影响线或“矩阵方法”标定出高精度的桥梁影响线，桥梁实际响应如应变数据通过实际车辆在桥上行驶得到[11]。当未知轴重F在桥上移动时，Moses算法利用桥梁响应理论值和实际值之差建立以未知轴重为变量的误差函数E，通过求解误差函数最小值获得车辆轴重的估计。误差函数E的表达式如式(1)所示。

(1)

式中，K表示总的时间步数，Sr为数据采集系统采集的桥梁实际响应，St为影响线理论计算出的车辆过桥时桥梁的理论响应。

利用最小二乘法求解上式误差函数的最小值，可求得车辆轴重如式(2)所示。

F=(ITI)-1ITSr

(2)

式中，F表示车辆轴重向量，I为基于荷载位置和影响线坐标建立的列满秩矩阵，上标T表示矩阵转置。

车辆总重G由算得的车辆各轴轴重进行叠加即可获得，表达式如式(3)所示。

(3)

式中，N表示车辆轴数。

2 车桥耦合振动分析模型

2.1 车辆模型

本文选用代表性的三轴车和五轴车两种车辆模型，总重分别为320.1 kN和392.4kN，车辆模型及静轴载分布图如图1所示，车型的详细参数可参见邓露等人研究模型[12]。

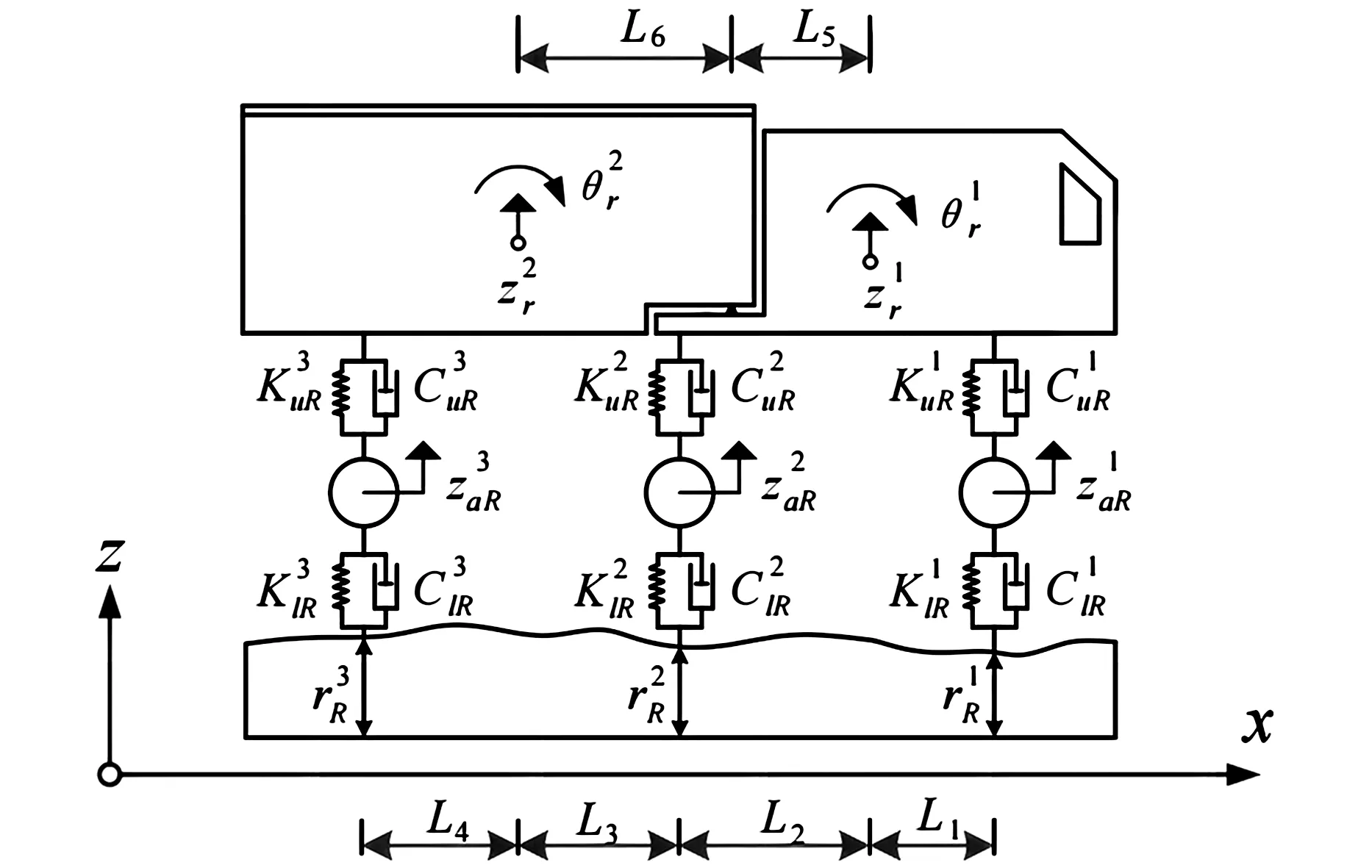
(a)三轴车侧视图

2.2 桥梁模型

本文共选用跨径为20m混凝土简支T梁桥，宽度为8.5m，梁高1.5m，基频为5.87Hz。利用有限元分析软件Ansys建立该桥有限元模型。设定车辆沿着桥梁加载位置中心线行驶，桥梁跨中横截面及车辆横向加载位置如图2所示。

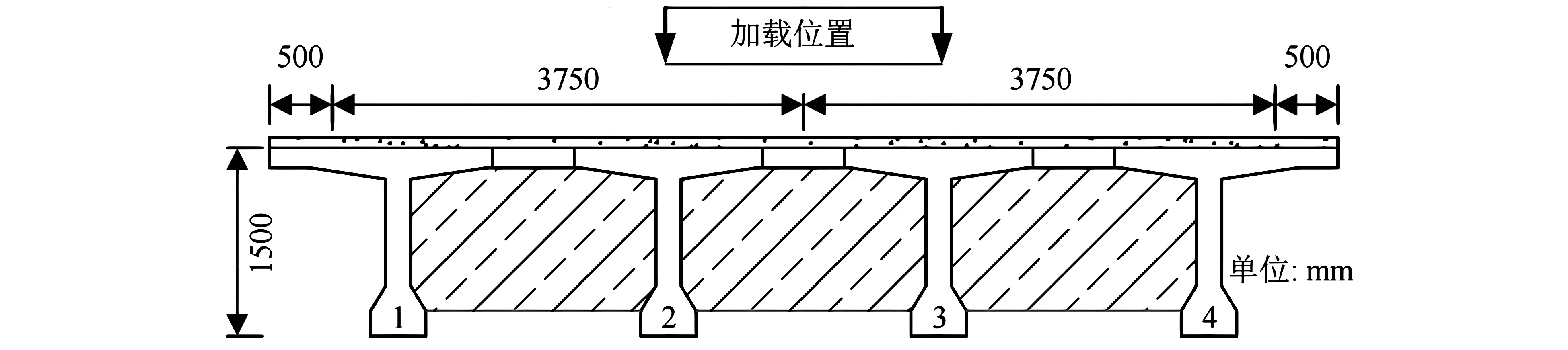
图2 桥梁横截面及车辆加载位置

2.3 噪声水平

为了更好地模拟车辆真实行驶环境，在数值模拟中加入了5%和10%两种级别的高斯白噪声。并且在进行车轴识别之前，利用Butterworth低通滤波器降低桥梁应变信号中可能由随机路面不平整度度或噪声对识别精度的影响。计算滤波器阻带频率的经验公式如式(4)所示。

(4)

式中，v为车辆行驶速度，L为桥梁长度。

2.4 桥面不平整度

桥面不平整度(road roughness condition，RSC)是影响车桥耦合振动的主要激励源，数值模拟中可通过高斯概率分布进行随机过程模拟。表达式如式(5)所示。

(5)

式中，φ( )为路面不平整度的功率谱密度[m2/(cycle/m)]；nj为波数(cycle/m)；θj为0～2π均匀分布的随机相位角。n0=0.1m-1(cycle/m)，为空间参考频率。

国际标准化组织(ISO，1995)[13]将RSC分为5个等级，包括非常好、好、一般、差、非常差，本文数值计算选用其中“非常好”、“好”、“一般”三种等级。

3 参数分析

基于图2所示混凝土简支T梁桥，利用数值模拟获得了多种工况下的桥梁动力响应，然后基于获得的应力对车辆的速度、轴距、轴重和总重进行了识别，并研究了车辆行驶速度、路面不平整度、噪音水平和桥头跳车等因素对识别精度的影响。具体的数值仿真工况如表1所示。

表1 数值模拟工况参数

3.1 速度、轴距识别

当路面粗糙度水平为“好”时，两种车型在不同车速条件下的车速和轴距的识别结果分别如表2和表3所示。需要说明的是，在动态称重系统中，对于间隔紧密的车轴的重量准确地识别非常困难。5轴卡车的后轴组中的三个轴间距非常紧密，在实际应用中将间距很小的一组轴当做一个单轴来识别[14-15]。此时，5轴卡车后轴组的等效真实轴重为后面三个轴的重量之和，即218.7kN。轴重的作用点是三个轴载合力的作用点，因此求得5轴车第二个车轴与等效后轴组之间的轴距为6.165m。

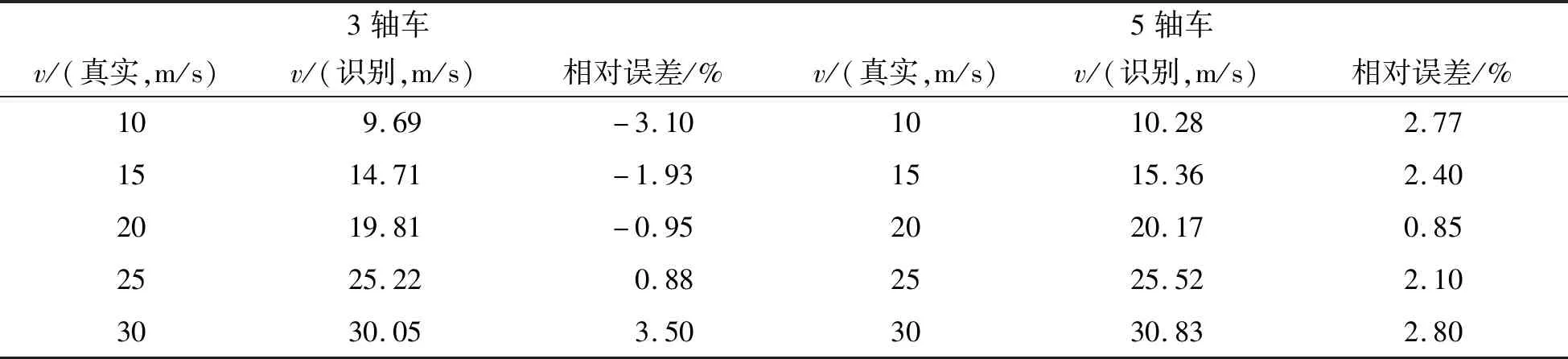
表2 两种车型速度识别结果

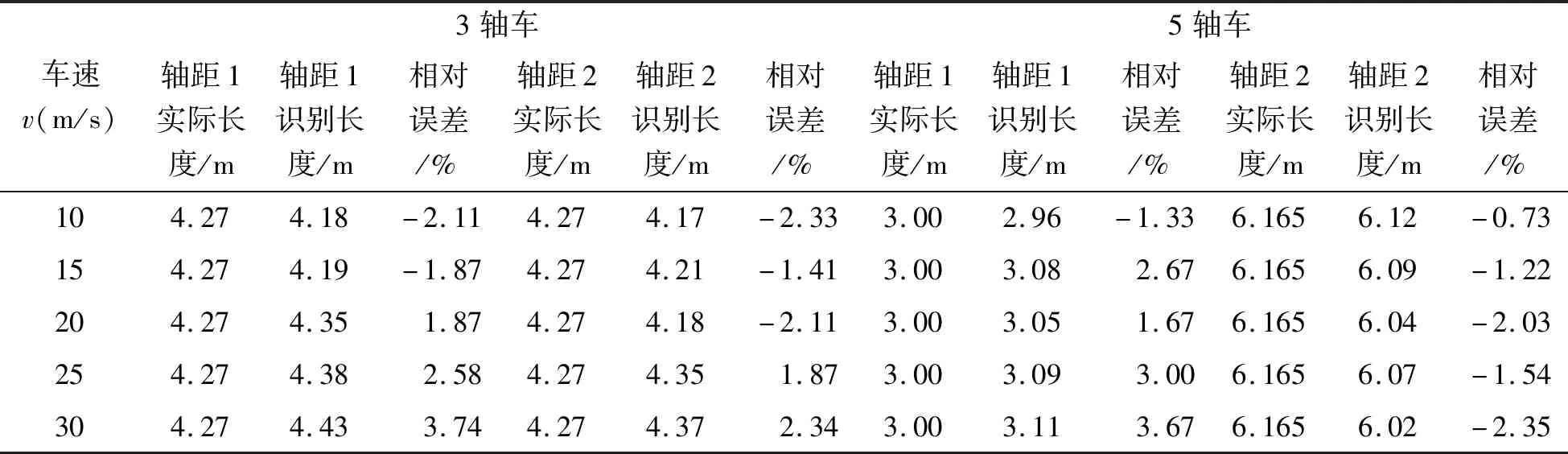
表3 两种车型轴距识别结果

从表2和表3可以看出：(1)在此工况下，五轴车模型所识别的车速和轴间距的相对误差最大值均小于4%，识别精度较高；三轴车速度识别相对误差最大值小于4%，轴间距识别相对误差最大值为4.45%。(2)对于两种车辆模型，轴距和车速识别误差最大值发生在速度最大的情况，即速度取值为30m/s时，说明该动态称重系统对高速行驶的车辆识别精度较低。(3)五轴车轴距2的识别长度结果都比真实长度小，这可能是因为第二个车轴与等效后轴组之间的轴距为等效轴距。

3.2 不同路面不平整度下的车重识别

不同路面不平整度下车重识别结果如表4所示，其中“AW1”、“AW2”和“AW3”分别表示车辆第1轴、第2轴和第3轴的识别结果，“GW”表示车辆总重的识别结果，车辆行驶速度v=10m/s。

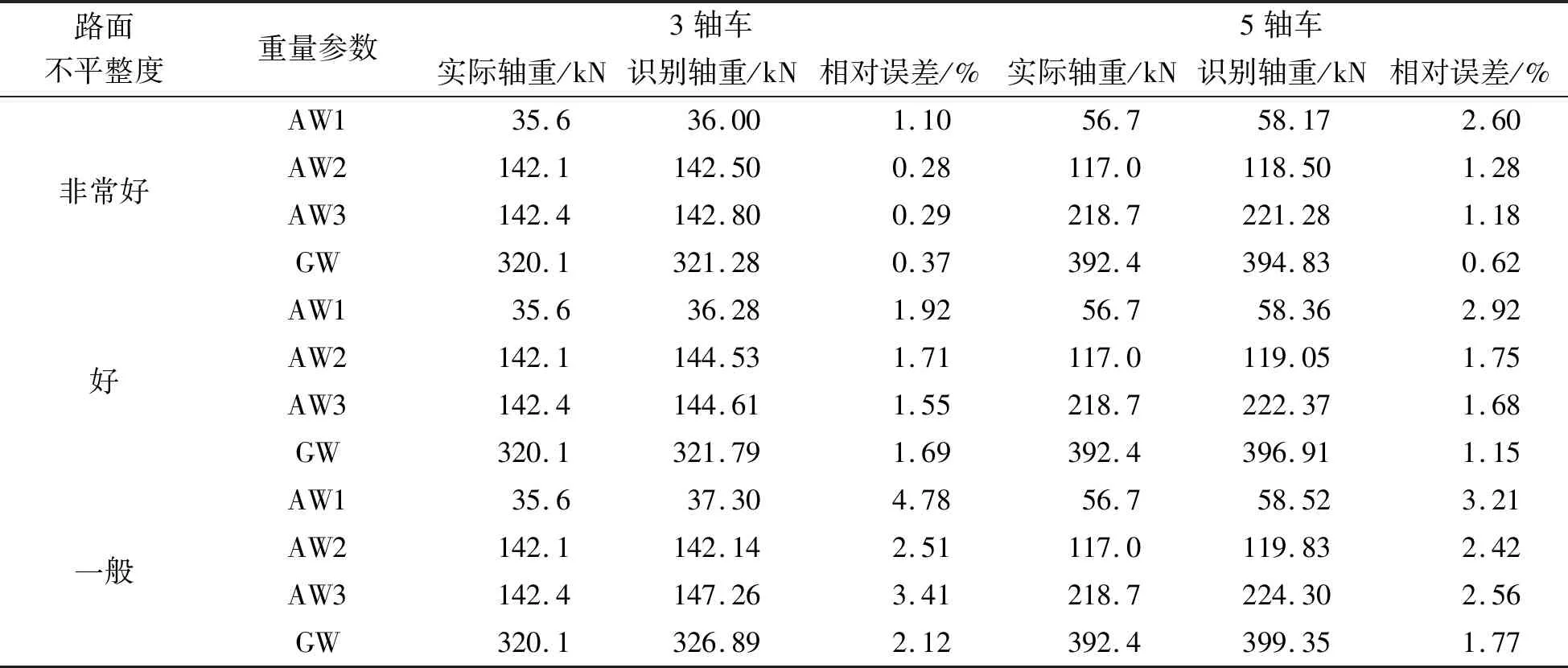
表4 不同路面不平整度下车重识别结果

从表4可以看出：(1)大部分情况下，路面不平整度越差，两种车型的轴重和总重识别误差均越大，这可能与不平整的路面会引起桥梁不规则振动有关[16]。以三轴车总重识别为例，当路面不平整度为“非常好”时，识别误差为0.37%；当路面不平整度为“好”时，识别误差为1.69%；当路面不平整度为“一般”时，识别误差为2.12%。(2)对于轴重的识别，三轴车和五轴车轴重识别误差分别不超过5%和3.5%，总重的识别误差均不超过2.5%。说明该动态称重系统对不同路面平整度下车辆的轴重及总重均有较高识别精度，并且，车辆总重的识别精度优于车辆轴重的识别精度。

3.3 不同行驶速度下的车重识别

不同行驶速度下车重识别的统计结果如表5所示，识别结果为三种路面不平整度下的平均值。

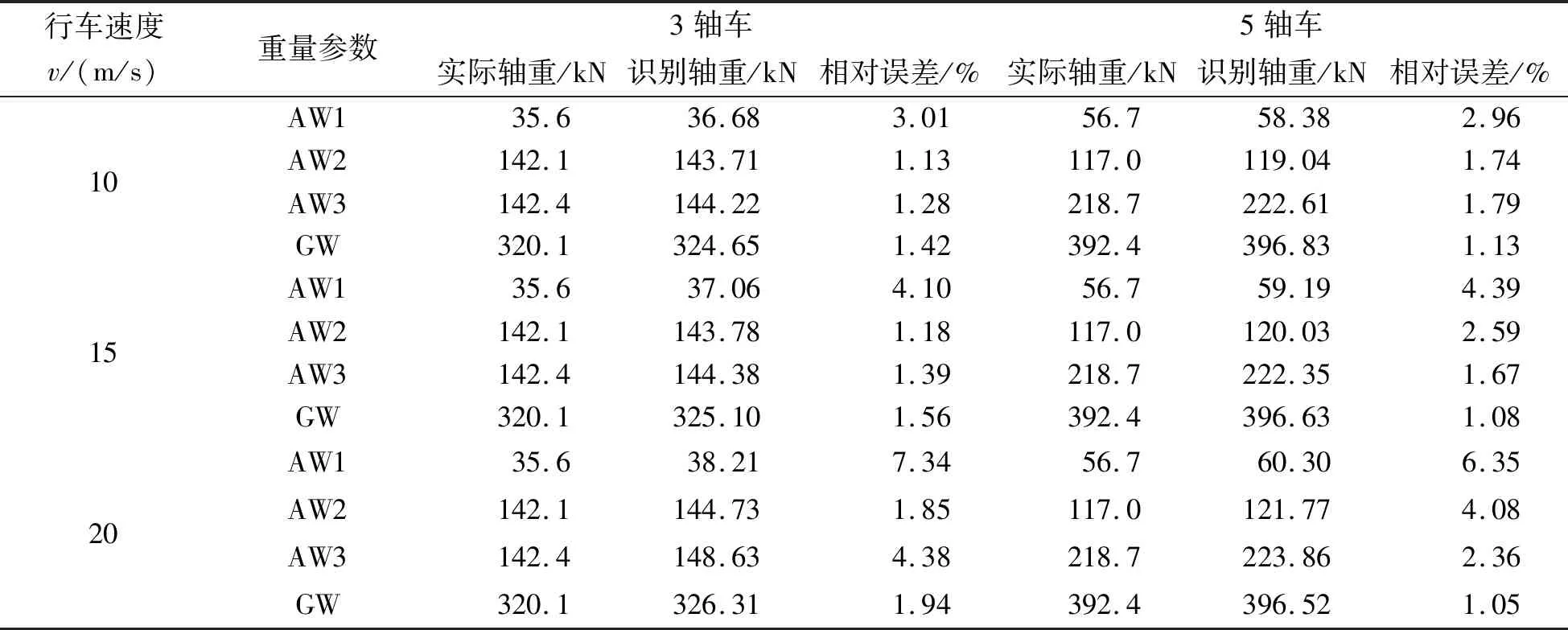
表5 不同行驶速度下车重识别结果

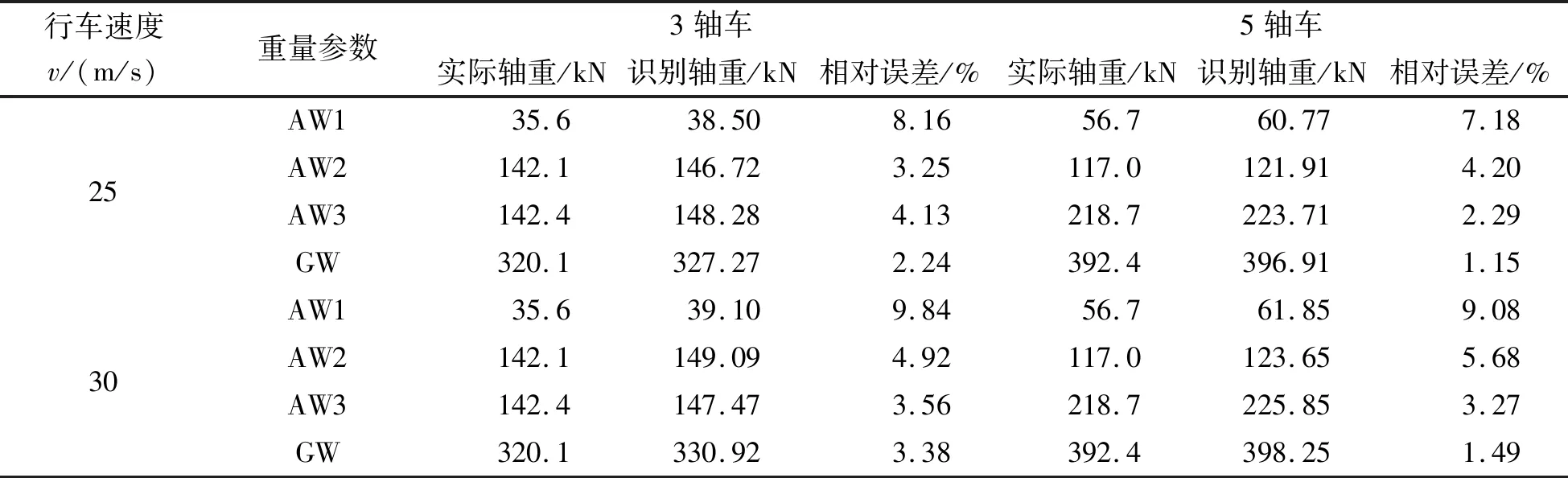
续表5

由表5可看出：(1)大部分工况下车辆行驶速度增大，车辆轴重和总重的识别误差均增大。以两种车辆模型的第二个轴重识别为例，当车速从10m/s增大到30m/s时，三轴车轴2的轴重识别误差从1.13%增大到4.92%，五轴车轴2的轴重识别误差从1.74%增大到5.68%。可见该称重系统对高速行驶的车辆的轴重识别精度较低，对中低速行驶的车辆有良好的适用性。特别是对于车辆较轻轴的轴重识别误差明显大于较重轴的识别误差；(2)在各行驶速度下，车辆总重的识别精度一般大于轴重的识别精度。且车辆总重的识别误差在大部分工况下的识别误差也是随车速的增大而增大，但最大识别误差仍小于3.5%。相同行驶速度下，五轴车的总重识别精度好于三轴车，进一步说明该算法对于较重的重量识别精度优于较轻的重量。