基于齿顶结构设计的面齿轮接触性能优化
2022-10-13陈思雨
鲁 锐,陈思雨,江 平,刘 波
(1.中国航发湖南动力机械研究所,湖南 株洲 412002;2.中南大学机电工程学院,长沙 410083)
0 引言
面齿轮副常用于交叉轴动力传输之中,主要由面齿轮和与面齿轮共轭的小齿轮组成。根据不同的工况要求,小齿轮可以设计为直齿轮、斜齿轮、锥齿轮等。由于面齿轮传动具有结构紧凑、传动平稳、动力分流效果好和对安装误差不敏感等特点,在军用领域中经常使用面齿轮传动代替锥齿轮传动以实现传动系统减质以及提高承载能力。尤其是在美军方联合美宇航局进行的先进旋翼机传动(The Advanced Rotorcraft Transmission,ART)项目中,将面齿轮传动运用到直升机主减速器中,取得了重大成功。波音公司的Apache武装直升机使用面齿轮传动代替传统的弧齿锥齿轮传动使得传动系统的总质量减少40%,承载能力提高了35%,且分流效果好,振动小。该项目在实践中充分证明了面齿轮传动的优势。随着航空发动机高功重比/高推重比的发展,对传动系统的承载能力要求越来越高,面齿轮在航空发动机传动系统中具有十分广泛的应用前景。
目前,关于面齿轮的研究大多集中于面齿轮系统的啮合特性和加工原理方面。Litvin等对面齿轮传动的啮合原理、啮合特性和加工原理做了大量研究,推导了面齿轮的齿面方程,并基于齿面接触分析(Tooth contact analysis,TCA)的方法进行面齿轮副的啮合特性研究;Chung T D和Chang S H建立了含有安装误差的直齿面齿轮分析模型,通过仿真分析得到了安装误差对面齿轮系统的影响;Guingand等研究了安装误差和加工误差对面齿轮系统啮合轨迹和接触应力的影响并进行了试验验证;Handschuh对直升机面齿轮传动系统的失效模式和承载能力进行了仿真和试验,表明表面点蚀是主要失效形式,但也发生了弯曲失效,齿轮构件上均出现点蚀或弯曲引起的齿裂纹;Wu等、曹茂鹏等、唐进元等进行了面齿轮3维建模、接触分析、面齿轮加工的系统性研究;李政民卿等利用有限元进行了面齿轮加载接触分析。随着有限元技术的发展,越来越多的学者采用有限元方法对面齿轮传动进行接触分析,计算其传递误差、接触区域和应力分布。
目前主要采用齿面修形的方法对面齿轮系统的传动性能优化,但面齿轮修形设计与加工较为复杂,关于齿顶结构对面齿轮系统啮合特性的影响规律罕有研究。本文针对1个存在边缘接触的面齿轮传动系统,采用齿顶倒圆和削顶的方式对面齿轮齿顶进行结构修改,分析2种方式对面齿轮接触特性的影响规律。
1 初始面齿轮模型
本文所分析的面齿轮系统基本参数见表1。基于面齿轮系统基本参数,利用有限元分析软件对表中的面齿轮系统进行加载接触分析,其最大接触应力曲线和云图如图1所示。从图中可见,在50 N·m的载荷作用下,面齿轮在啮合过程中最大接触应力为1254 MPa,已超过了材料对应的许用接触应力1080 MPa。从图1(b)中可见,最大接触应力发生在面齿轮齿顶位置,是由于存在边缘接触而导致的应力集中。负载为50 N·m时最大接触应力已超过材料许用应力,而在正常工况下面齿轮的负载可达1300 N·m左右,因此该面齿轮模型无法满足实际的工程要求,需要对原模型进行性能优化。本文主要通过面齿轮齿顶倒圆和齿顶削顶的方法来提高端面齿轮传动系统的性能。

表1 面齿轮系统基本参数
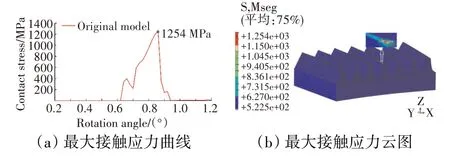
图1 初始面齿轮模型最大接触应力曲线和云图
2 面齿轮齿顶结构优化设计
2.1 面齿轮齿顶倒圆对其接触性能的影响
参考直齿轮齿顶倒圆半径大小选择经验,设置了3种面齿轮齿顶倒圆半径,见表2。其中为面齿轮模数。基于所设置的3种倒圆方案,分别进行有限元建模仿真分析,并将负载增大到1500 N·m。

表2 3种面齿轮倒圆方案
3种倒圆模型所对应的啮合力曲线如图2所示。从图中可见,3种方案所对应的最大啮合力分别为5109、4448和4788 N。此外,对于0.10模型,当轮齿即将退出啮合时啮合力存在突变,结合该时刻的应力云图(如图3所示)可知此时面齿轮发生了边缘接触导致应力集中所造成的。
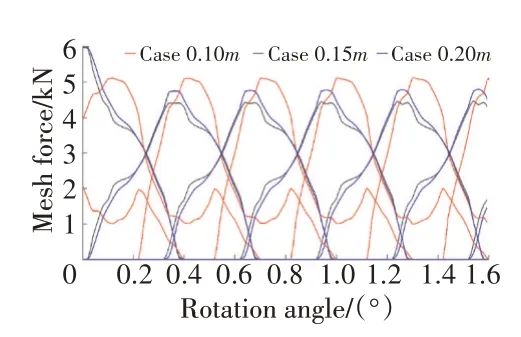
图2 3种倒圆模型所对应的啮合力曲线

图3 倒圆方案1啮合力突变点对应的应力
3种倒圆模型对应的最大接触应力曲线如图4所示。从图中可见,3种模型所对应的最大接触应力依次为2953、662和542 MPa。3种倒圆模型最大接触应力时刻所对应的应力云图如图5所示。从图中可见,0.10模型依然存在边缘接触,这是该模型接触应力较大的原因;0.15模型的最大接触应力相比0.10模型的明显减小,但其对应的啮合位置依旧在齿顶附近;相对于其他2种方案,0.20模型的最大接触应力不仅明显减小,且其对应的啮合位置远离齿顶。
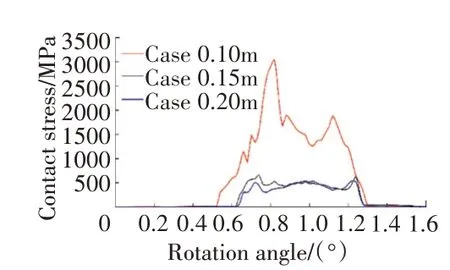
图4 3种倒圆模型对应的最大接触应力曲线

图5 3种倒圆模型对应的最大接触应力
根据文献[1]提供的齿轮重合度计算方法,齿轮重合度的计算方法为


式中:Δ为单个轮齿参与啮合对应的时间;Δ为相邻轮齿进行啮合的时间差。
基于有限元仿真分析结果和公式,3种模型所对应的重合度依次为2.6、2.3和2.2。可见随着倒圆半径的增大,面齿轮的重合度逐渐减小。考虑到随着重合度减小,面齿轮的承载能力会逐渐降低。方案3(0.20模型)既可以避免边缘接触,又可以减小齿顶倒圆对承载能力的影响,为最优的齿顶倒圆方案。
2.2 面齿轮齿顶削顶对其接触性能的影响
在经典板理论中,可以通过改变板的形状如改变平板边的个数、挖孔等方式来改变平板的刚度、应力等性质。基于此原理,将齿轮的齿面看作1块板,没削顶时是1块矩形板;如果齿面被切掉1个角,齿面就会从四边形变成五边形,齿轮的性能也会相应改变。基于此假设,采用面齿轮齿顶削顶的方式对面齿轮系统进行优化。
面齿轮齿顶削顶如图6所示。在直齿面齿轮安装坐标系下,在平面内作与轴成角的射线。射线绕轴旋转得到1个伞形曲面,并将曲面以上部分切掉,得到面齿轮削顶模型。本文共设置了3种削顶方案,见表3。从前文分析可知,采用0.20齿顶倒圆时面齿轮啮合性能较好,因此对削顶模型也进行了0.20倒角。
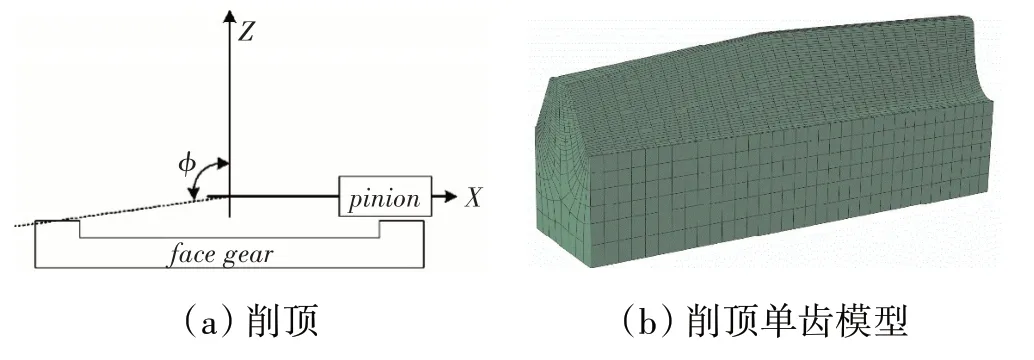
图6 面齿轮齿顶削顶

表3 面齿轮削顶方案
3种削顶模型对应的啮合力、最大接触应力曲线以及应力云图如图7、8所示。从图7中可见,97.2和97.5削顶模型的啮合力曲线几乎一致,在啮合过程中最大啮合力为4677 N,重合度均为2.2。与无削顶0.20倒角模型相比,啮合力大小几乎相同,重合度也相同。对于97.8削顶模型,其啮合力明显增大,最大啮合力为5768 N,且重合度降低到2.07。从图8中可见,97.8削顶模型的接触应力与其他2种模型的相比非常大,其最大值达到1449 MPa,超过了允许的接触应力。而97.2和97.5模型的最大接触应力分别为626、535 MPa。

图7 3种削顶模型对应的啮合力曲线

图8 3种削顶模型对应的最大接触应力曲线
3种削顶模型对应的最大接触应力云图和刚进入啮合时的啮合点位置如图9、10所示。从图中可见,97.8削顶模型的最大接触应力出现在齿尖边缘,而其他2种模型的最大接触应力都在轮齿表面。因此,97.8的削顶使面齿轮啮合出现边缘接触现象,这是因为较大的削顶角度改变了齿面接触面积。此外,97.5削顶不影响接触面积,所以啮合力和重合度与0.20倒圆模型的相同。而97.8削顶模型改变了齿面接触区域,因此啮合力和重合度发生了变化。因此,削顶时必须注意削顶角度不能影响到齿轮副啮合轨迹和接触区域。

图9 3种削顶模型对应的最大接触应力云图

图10 3种削顶模型刚进入啮合时的啮合点位置
当密度为7850 kg·m时,各削顶模型的质量和转动惯量计算见表4。从表中可见,3种齿形切削模型的质量比原模型的分别减少了0.12%、0.8%和2.6%。对于面齿轮轻量化设计,合适的切齿是一种方便有效的方法。因此综合以上分析,97.5削顶为最优削顶方案。

表4 削顶模型对应的质量和转动惯量
3 结论
(1)与原始面齿轮模型相比,齿顶倒圆可以有效改善面齿轮的边缘接触问题和减小最大接触应力,但随着倒圆半径的增大,面齿轮的重合度逐渐减小,因此齿轮倒圆存在合理的区间,通过分析发现,文中模型倒圆半径为0.20倍模数为较优方案;
(2)削顶可以一定程度上减轻面齿轮传动系统的质量,为系统轻量化设计提供设计方案。一定程度的削顶对面齿轮重合度和接触应力影响较小,但较大的削顶会使齿轮发生边缘接触,从而使齿轮接触应力增大。通过分析发现,文中模型削顶角度为97.5°为较优方案。
