时滞反馈下高速磁悬浮轴承转子系统的稳定性分析
2022-10-13郑凯
郑 凯
(1.中国航发沈阳发动机研究所,2.中国航空发动机集团航空发动机动力传输重点实验室:沈阳 110015)
0 引言
磁悬浮轴承具有转速高、无需润滑、工作温度范围广、可测可控性好等诸多优点。作为航空多电发动机的重要组成部分,各国研究机构和学者对其高度关注,并在其控制方法、动力学分析和试验应用等方面开展了大量研究工作。最近的研究发现,一些在机电系统中常被忽略的微小时滞可能对高速运转的磁悬浮轴承转子系统的稳定性和动态性能产生很大影响。这些时滞包括位移信号的采集、处理、转换、控制算法在CPU中的运算等过程所消耗的时间,以及执行单元中功率放大器的饱和效应和电磁铁线圈中的涡流损耗和磁滞特性所产生的滞后效应等,其量级为几十微秒,在系统相对简单、时滞环节不多且对于系统动力行为无严格限制的情况下,忽略其产生的效应并无不妥。但考虑到航空发动机等重要设备的高可靠性要求,对于工作在苛刻条件下的复杂机电系统,其设计技术和控制理论研究必须构筑在更加严密的体系框架之下,进一步的探索也必须认真考虑时滞的作用。
目前对于磁悬浮轴承时滞问题的研究已经引起了一些关注。Wang等讨论了1个含有输入时滞的单自由度系统的稳定性与Hopf分岔问题,利用中心流形约化和范式方法讨论了Hopf分岔的方向及分岔周期解的稳定性;Jiang等在其基础上着重研究了当系统特征方程有1个零特征根和1对纯虚根的情形,给出了完整的稳定性分岔分析;Ji等研究了由PD反馈控制的简单Jeffcott转子系统的时滞问题,证明了较小的时滞依然可以影响系统的非线性响应,又将研究扩展到较复杂的2自由度径向转子系统。上述研究发现,当时滞超过1个关键点时,会发生Hopf分叉,转子运动由平衡点解转变为稳定的周期解;而当时滞未达到关键点时,其对系统动态性能的影响可以忽略。值得注意的是,以往的研究大多关注于转子系统静止或低速转动下的平衡点解,对其产生影响的时滞数量级可能在毫秒级,对于机电控制系统的时滞一般是在微秒级,如此小的时滞对平衡点解的影响几乎可以忽略不计。而在实际应用中,电磁轴承所支撑的转子运转于高速状态下,且由于转子偏心的存在,其运动的固有解为受迫振动的周期解,即使是微秒级时滞,也可能与转子高速涡动的周期数量级接近,进而可能对转子系统的动态性能和稳定性产生重大影响。
本文着重分析了微小时滞对于高速转子受迫振动周期解的影响,利用数值方法讨论了转子系统周期解随时滞的变化规律以及稳定性切换问题。
1 磁悬浮轴承系统时滞动力学模型
在实际中磁悬浮轴承-转子系统可以简化为2自由度刚性转子系统,如图1所示,、方向上2对磁极对称安装。

图1 2自由度电磁轴承-转子系统
当转子处于几何中心时,到电磁铁的气隙都为。为了建立磁场,同一自由度上两侧的电磁铁线圈中通有相等的电流,称为偏磁电流。以方向为例,当转子发生偏移,则转子与左侧磁铁之间的距离为+,与右侧电磁铁之间的气隙为-。此时控制器输出的控制电流为,依照差动模式驱动电磁铁,则两侧磁极中的电流分别为+和-,保证将转子拉回到平衡位置,在方向上2个磁极产生的电磁力F 为

式中:为电磁力常数;、分别为、方向上的位移。
将、方向自由度之间的几何耦合效应考虑在内,则转子在、方向上的动态方程分别为

式中:为几何耦合系数;为转子质量;f 、f 分别为、方向上的偏心力,=sin(),=cos()。
若控制器选用PD控制器,假设2个自由度控制回路中的时滞大小皆为,即控制器实际依照时刻的系统状态来施加控制,则控制电流i和i可表示为
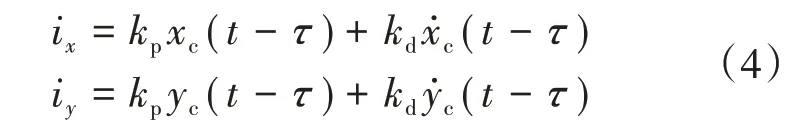
式中:为比例控制系数;为微分控制系数。
由于多尺度法等近似解析方法推导过程冗繁,所能处理问题的维数较小,对于自由度较多且各自由度之间存在耦合的系统分析起来比较困难,因此本文采用厚度为时滞的庞加莱板打靶法,以考虑了极间耦合效应的2自由度刚性转子系统为研究对象,对其时滞动力学问题进行研究。
2 数值分析方法
本文借助文献[14]中改进打靶法的思想对磁悬浮轴承系统周期解的时滞问题进行研究,将求解系统周期解的过程转化为求取“厚度为”的庞加莱板上的不动弧,如图2所示。
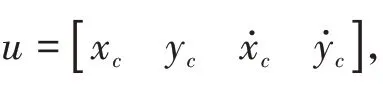

图2 庞加莱板上的不动弧

将时间区间[-,]分为-1个等距小区间,系统在时间区间[-,]内的运行弧线上可以分为个节点:
u =(+t ),t =-+(-1)/(-1),=1,2,,,取=[...u ],定义为庞加莱映射算子,则系统可表示为庞加莱映射的形式

其中()表示系统以()为初始值经历1个庞加莱映射周期后的状态,而求解系统(5)的周期解可以转化为求取“厚度为”的庞加莱板上的不动弧,不动弧上的节点满足*=(*)。
选取庞加莱板初始弧线上节点,对式(6)采用牛顿-拉普森迭代公式有

式中:为新的迭代节点;为单位方阵;()为庞加莱算子在处的雅可比矩阵。
取,分别为(),(-)的偏微分算子,式(7)中((),())可以通过微分方程组
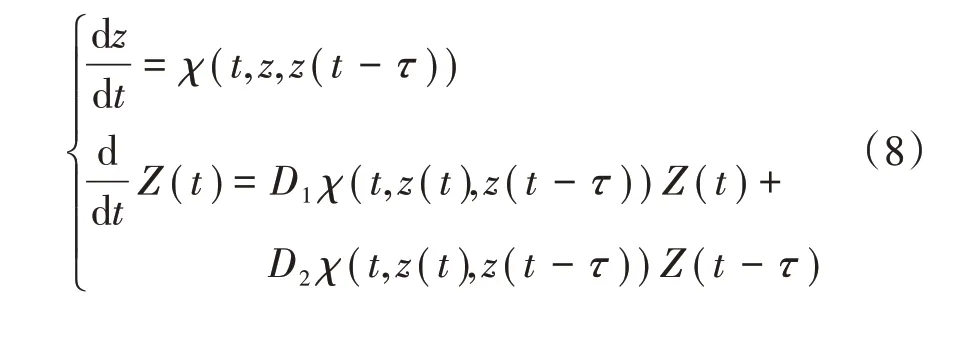
采用数值积分法对1个庞加莱周期求积分获得,即
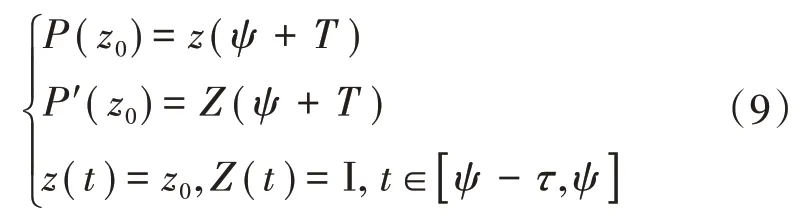
将所求得的(),()代入式(7)计算出新的迭代点,经过反复迭代得到系统的周期解,迭代过程的流程如图3所示。
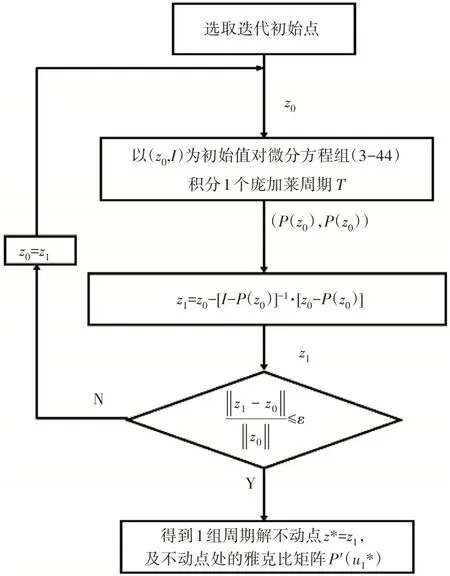
图3 迭代流程
经过上述迭代过程,最终得到系统的周期解不动弧上的1组节点*,同时求得庞加莱算子在*处的雅可比矩阵(*)。根据Floquet理论,矩阵(u *)的特征值即为所得周期解的Floquet乘子,且有:
(1)若Floquet乘子模的最大值小于1,系统周期解是稳定的;
(2)若Floquet乘子模的最大值大于1,系统周期解是不稳定的;
(3)若Floquet乘子模的最大值等于1,系统周期解处于临界稳定状态。
由此对所得周期解的稳定性进行判定。
3 数值分析结果
选取1个实际的电磁轴承刚性转子系统作为研究对象,系统参数如下。
(1)转子:质量=9.6 kg,偏心距=0.02 mm。
(2)电磁轴承:=4 A,=0.4 mm,=8.63×10Nm/A,=0.16/。
(3)控制器参数:k =89280A/m,k =5A·s/m。
设定转子转速为25000 r/min,利用第2章中所描述的算法在不同时滞下进行计算分析,系统周期解的振幅随时滞的变化如图4所示。从图中可见,随着时滞的延长,振幅缓慢增大,时滞对于稳定周期解振幅的影响并不明显。
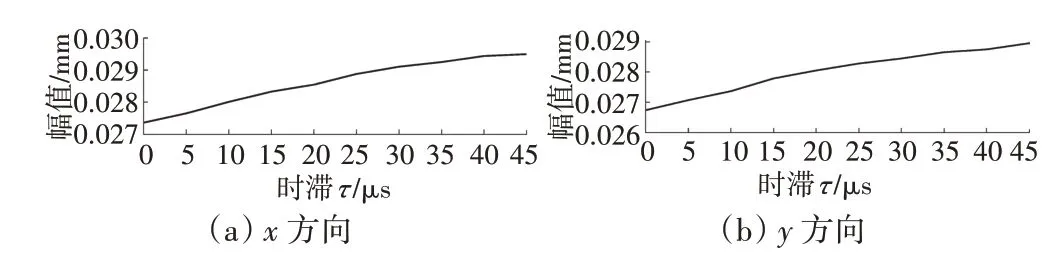
图4 周期解振幅随时滞的变化
不同时滞下计算出的模最大的Floquet乘子如图5所示。从图中可见,随着时滞的延长,Floquet乘子逐渐接近单位圆,当时滞达到43μs时,以共轭复数方式穿出单位圆,转子系统不再具有稳定的周期解。
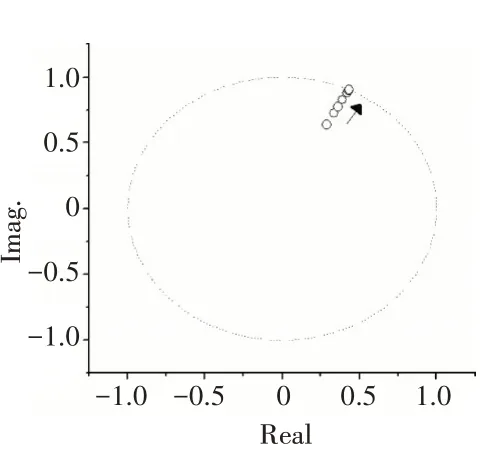
图5 模最大的Floquet乘子
时滞分别为0、40.0、43.2、44.0μs时转子的轴心轨迹如图6所示。从图中可见,随着时滞的延长,转子运动从稳定的周期运动(图6(a)、(b))转变为概周期运动(图6(c)),而当时滞达到44μs时,转子系统失稳(图6(d))。

图6 不同时滞下转子的轴心轨迹
对于时滞在不同转速下对转子系统稳定性的影响的进一步研究发现,在转速较低的情况下,引起转子系统失稳的时滞大小都在毫秒级,远远高于一般机电控制系统中可能出现的时滞,而当转速升高至约18000 r/min时,失稳时滞缩短至只有60μs。各转速下的失稳时滞如图7所示。从图中可见,随转速升高,能够使转子系统周期解失稳的时滞明显缩短,说明随转速的升高,微小时滞对于转子系统稳定性的影响也更为显著。当转速升高到60000 r/min时,转子系统在时滞约为19μs的情况下就可能失稳(如图8所示),而如此短的时滞对于采用数字控制器的电磁轴承系统来说是难以避免的。

图7 各转速下的失稳时滞

图8 转子轴心轨迹(ω=60000 r/min、τ=19μs)
4 结束语
本文研究了时滞对于不平衡扰动下磁悬浮轴承转子周期解的影响,结果表明,对于高速转子系统,在控制反馈回路中即使存在微秒级的微小时滞,也可能对系统的动态特性和稳定性产生重大影响,使得动态性能降低甚至失稳;并且随着转速升高,时滞的影响更为显著。
因此进行高速转子系统设计和控制时,需要考虑时滞的影响。目前对类似于电磁轴承等复杂机电系统的时滞问题的研究在国内外均尚处于初级阶段,对系统时滞的精确测算以及时滞系统的鲁棒控制等问题还有待进一步研究。
