基于性能非线性退化统计模型的发动机剩余寿命预测

2022-10-13郑天翔李印龙

航空发动机 2022年4期

郭庆，郑天翔，李印龙

（中国民航大学航空工程学院，天津 300300）

0 引言

航空发动机是航空器的“心脏”，其健康状态对保证航空器正常运转具有重要意义，但是航空发动机由于长时间在复杂多变的恶劣环境下运行，其性能会随着服役时间延长出现退化现象，并且在退化到某一阈值时，最终需将发动机下厂翻修。为了准确地评估发动机的健康状态，需对发动机可能发生的故障及时处理，并及时地配合发动机的运行规划和合适的维护决策，减少灾难性事故的发生，减小因事故造成的损失，因此需要通过监测航空发动机性能退化数据，构建相应的退化模型，进而预测发动机的实时剩余寿命。

随着传感器技术和预测技术的迅速发展，从视情维修中发展出了1个重要方向——预测维修，而作为实现预测维修的核心技术，寿命预测近年来已经成为中国研究的热点之一。主流的研究方法可分为基于模型的方法和基于数据驱动的方法。基于模型的方法需要借助其故障模式和失效机理建立模型来评估其健康状态，典型的预测方法是利用统计方法对发动机寿命数据进行统计分析，进而得到其寿命分布，此外还有随机损伤传播模型等；而基于数据驱动的方法不需要建立发动机的性能模型，通过状态监测数据和历史故障数据进行预测，诊断方法包括神经网络方法、支持向量机法、相关向量机法、自回归（Auto Regressive，AR）模型等。然而在剩余寿命预测领域，设备的性能退化过程多以关于时间的线性函数为主，鲜有研究非线性退化的情况，对此王小林等利用非线性Wiener过程对产品性能退化过程建模，表明非线性的退化过程更能反映某些复杂设备的性能退化轨迹。在航空发动机研制中受材料、加工条件等因素的影响，使得同类型产品的性能退化过程存在差异性，需要在剩余寿命预测中加以考虑。

针对航空发动机性能退化的非线性、不确定性，本文基于传感器得到的发动机监测数据，构建非线性性能退化统计模型，利用贝叶斯准则对参数进行实时更新，开展发动机实时剩余寿命预测。

1 非线性性能退化建模

1.1 非线性退化数据统计模型

在航空发动机退化过程中，按照时间顺序，根据传感器所测得的退化数据分析系统主要性能的退化过程，并建立退化轨道，退化轨道是系统性能退化的真实写照。具体地，性能退化过程表示为

式中：X(t)为系统在时间t处的真实退化值；y(t)=(y(t),…,y(t))为q×1的矩阵，其中y(t)(l=1,2,…,q)是t的已知函数；α为q×1的随机变量，且E(α)=μ，Cov(α)=∑。

式（1）给出的轨道中关于t的函数形式可以是线性的，也可以是非线性的。

由于受测量仪器精度和环境噪声影响，发动传感器监测的衰退数据不可避免地存在测量误差，因此引入随机误差ε描述性能退化过程中的测量不确定性

据此对n台发动机在m个给定时间点的数据统计模型综合如下

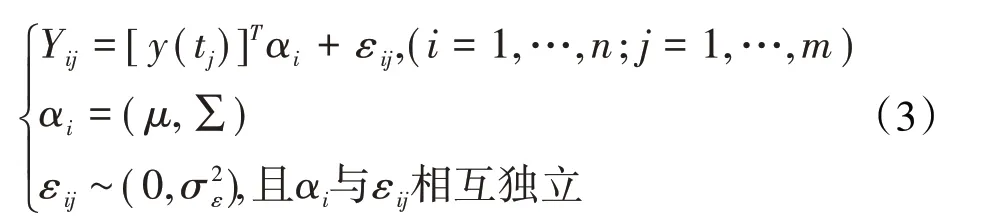
式中：α为第i个发动机的随机参数向量，用以描述个体间的差异不确定性，可看作是来自某概率分布α～N(μ,∑)的1个样本，并且与ε相互独立。

实际上，由于受初始条件、制造工艺、操作和环境等因素的相互影响，即使同类型的航空发动机，不同个体间的性能退化过程也往往存在着差异，且在某一时刻的性能衰退量也是随机的，这些随机波动时大时小，时正时负，很难控制，最后综合地表现在退化曲线和失效时间上。发动机性能退化符合非线性退化过程，故在发动机性能衰退建模中，考虑发动机退化轨道模型中关于t的函数形式采用指数模型

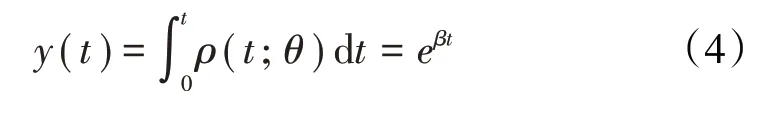
综上所述，基于退化轨迹的发动机性能退化模型采用满足于退化带有随机效应的非线性退化模型，且为了不失一般性，初始值Y(0)设为零

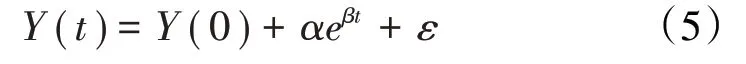
1.2 非线性退化模型参数估计

对于式（2），若Rank(X)=q，则μ,σ,∑分别有以下无偏估计。

（1）随机参数α均值μ的最小二乘估计。

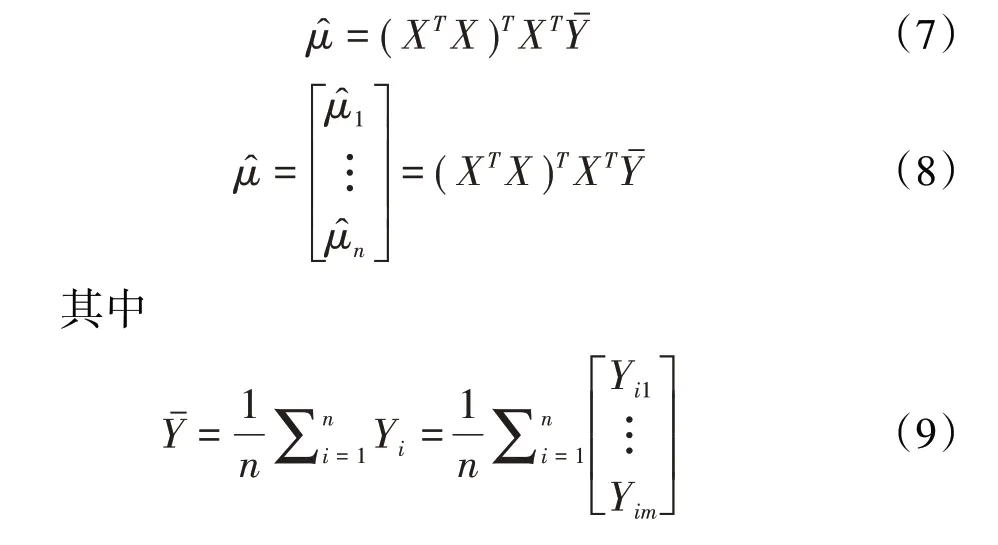
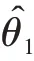
2 发动机剩余寿命预测

2.1 贝叶斯更新参数

由于受到内部因素和外部因素的影响，航空发动机性能退化过程存在着不确定性，为了减小不确定性对航空发动机剩余寿命预测结果准确性的影响，对于具体运行的发动机，根据贝叶斯准则，利用其运行过程中实时的监测数据对模型中的随机参数的概率分布进行更新，使得退化建模的结果更加符合该发动机实际的运行情况。因此，在时刻，该发动机所有的传感数据为={(t ),≤t ≤t }，并且令X =(t )，基于的先验分布和历史数据，根据Bayesian链式规则得到模型参数α的后验分布

2.2 个体发动机剩余寿命预测

航空发动机的剩余寿命是指从当前时刻开始，随着服役时间的延长，表征发动机健康水平的性能衰退状态{ }

(),≥0首次达到红线值的时间。基于首达时间定义发动机的寿命过于严格，当性能退化量首次达到红线值时，发动机可能仅仅是性能降低，并未失效，但从安全角度上考虑，此时应该停止使用。

因此由退化轨道()首次达到红线值时可以确定1个失效分布，这是退化模型参数的分布，发动机的使用寿命可以定义为

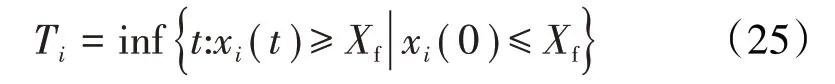
式中：T 为随机变量，为第个发动机的寿命；为发动机的红线值。

通常红线值是确定值，但在发动机的退化过程中存在随机性，不同类型、批次的发动机在真实失效时对应的退化量不尽相同。为了减少不确定性，在相同失效模式和操作条件下，发动机的红线值可以通过使待定红线值与不同发动机失效时刻对应的退化量的方差最小值来确定

对于固定的X ，与L 的分布依赖于基本轨道参数(α;)。在退化轨道的函数形式是线性的情况下，有可能写出()的显式表达式；在函数形式是非线性的情况下，这种显式表达式很难得到，采用数值仿真方法估计()的表达式是很好的解决方式。

为了避免上述多重积分计算可能带来的困难，本文采用蒙特卡洛方法来模拟发动机退化过程，蒙特卡洛仿真流程如图1所示。利用随机数来描述发动机性能状态随运行时间的变化，将发动机性能退化的确定性问题转化为随机问题。在发动机运行过程中，通过模拟总体样本发动机退化行为的规律和个体随机发生相互作用，对大量的随机事件追踪和统计来获得发动机的性能状态。

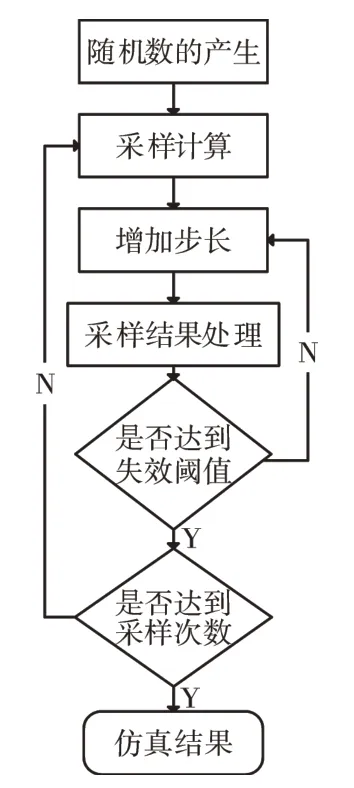
图1 蒙特卡洛仿真流程

蒙特卡洛方法解题主要步骤为：

（1）描述或构造概率过程。对本身具有随机性的问题建立正确描述问题的概率统计模型，模型的概率分布可以很好地反映所求问题。

（2）概率分布抽样。概率模型确定后，根据模型进行大量随机试验获得随机变量的试验值。确定随机变量的产生方法，包括随机数或伪随机数的产生及根据概率统计模型对随机数进行抽样，根据试验规则进行大量相互独立的随机抽样试验。

（3）得到各统计量的估计值。根据概率模型进行模拟试验后，分析试验结果的数学特性。

3 实例验证

本试验采用C-MAPSS数据集中FD001数据集进行试验验证，C-MAPSS数据集是基于NASA出品的涡扇发动机模拟模型C-MAPSS，通过模拟各种操作条件并加入不同程度的衰退故障生成的数据集，广泛地应用于各种工况下的发动机性能退化试验。该数据集模拟了发动机在单工况单故障情形下模拟运行产生的退化以及失效数据，共包含了100台失效的发动机全寿命退化数据，每组监测数据包括21个传感器的监测数据。

根据工程实践可知，航空发动机的性能衰退和故障通常表现在排气温度裕度值（Engine Gas Temperature Margin，EGTM）的衰减，因此EGTM是表征发动机健康状态的1个重要指标。本文使用与EGTM成正相关关系的排气温度裕度（Exhaust Gas Temperature，EGT）作为表征发动机退化状态的性能参数。为验证非线性退化轨道模型在航空发动机剩余寿命预测中的准确性，选择100台全寿命周期的前80台发动机EGT历史监测数据作为训练组，后20台发动机的EGT监测数据用作实时更新测试。

由于初始数据有着极大的随机特性，并且在每个监测参数数据中都加入了大量随机噪点，该数据集存在一定未知程度的初始退化，不满足于建模研究，需要对数据进行预处理（如图2所示），即在不改变数据的数字特征的情况下，降低数据的数量级。随机取出1台发动机对其性能参数采用局部加权平均法进行平滑处理

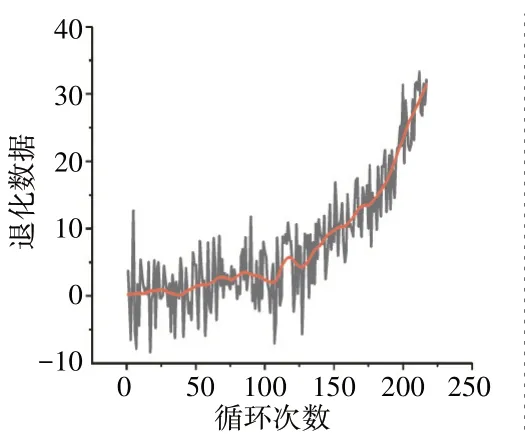
图2 数据预处理

式中：为与当前中心点x 关联的跨度内的相邻点；d 为沿横坐标x 到跨度内最远的相邻点的距离。

采用参数估计方法得到的参数估计值的结果见表1。

表1 参数估计结果

以表1中的参数估计值为先验信息，利用式（23）、（24）对退化模型中的随机参数的均值和方差进行实时更新（其结果如图3、4所示），实现对发动机健康情况的实时跟踪。

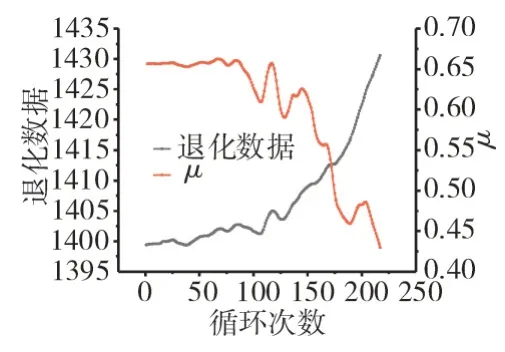
图3 α均值更新结果

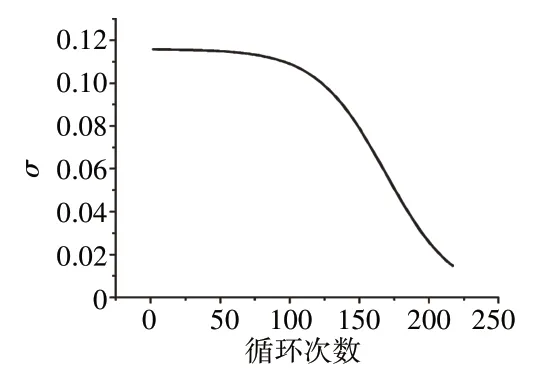
图4 α方差更新结果

从图3、4中可见，退化模型的参数可以随着衰退数据的积累动态更新，并且每当获得1条新的衰退数据，模型的参数可以自适应地估计和更新，从而得到更新后的剩余寿命的概率密度函数PDF（PDF，Probability Density Function），弥补了历史数据和先验信息的不足，表明了本文所提方法能够实时跟踪发动机的及时健康情况。

随机参数的均值和方差随着发动机退化数据的增加不断更新。从图3中可见，在前100个循环中发动机性能退化趋势平缓，随机参数的更新结果变化较小，发动机健康状态基本不变。随着运行时间的增加，发动机退化趋势变大，随机参数均值出现一定范围的波动，并且其变化趋势随监测数据变化而出现不同程度地波动；而随机参数方差的更新演化趋势表明，随着退化数据的不断增加，对随机参数估计值的不确定性逐渐减弱。

蒙特卡洛仿真结果数据就是发动机剩余寿命数据，对其以柯尔莫哥洛夫-斯米尔诺夫（Kolmogorov-Smirnov，K-S）检验标准进行分布拟合，拟合结果见表2。

表2 观测显著性水平P值

值是统计检验的观测显著性水平，＞0.05时，不排除当前拟合的分布形式。表2中数据展示了在发动机运行60、120和180循环时，蒙特卡洛对发动机剩余寿命预测仿真结果。显然指数分布的＜0.05，则拒绝0.05水平的分布，而正态分布、对数正态分布和Gamma分布的＞0.05且相差不大，以发动机在60循环时的剩余寿命预测为例，3种分布拟合如图5所示。从图中可见，3种分布趋势相近，都是数据良好的模型。

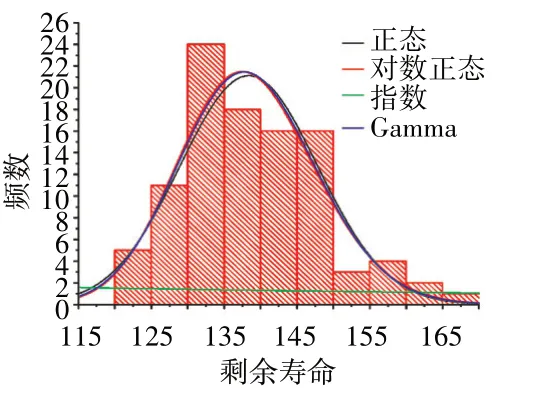
图5 3种分布拟合

3种分布拟合优度值见表3。从表中可见，在分布拟合相近的3种分布形式，正态分布拟合优度值比其他2种分布的更接近仿真数据分布模型得到的结果。K-S检验结果如图6所示。从图中可见，样本数据点基本在1条直线上且在95%置信带内，因此选择正态分布来描述发动机的剩余寿命预测PDF，使用剩余寿命仿真结果的期望值作为发动机剩余寿命的预测值。

图6 K-S检验结果

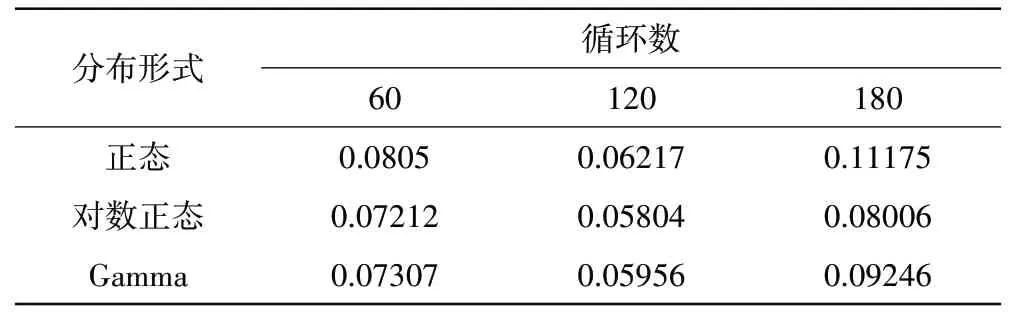
表3 拟合优度值

对发动机剩余寿命预测结果如图7所示。从图7（a）中可见，对发动机剩余寿命预测的误差集中在发动机运行早期，在中后期的相对误差明显减小；在发动机运行后期的剩余寿命预测精度较发动机早期和中期的明显提高。

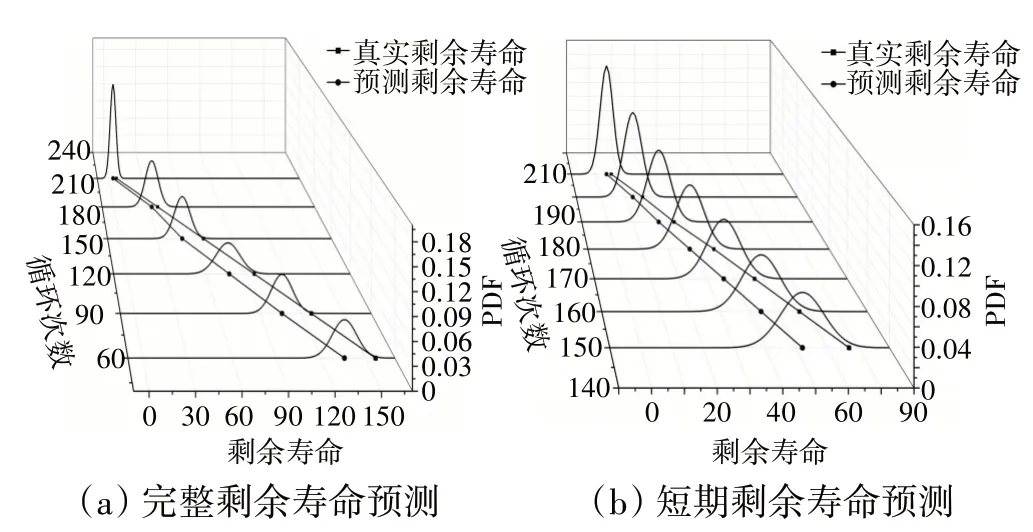
图7 剩余寿命预测结果

从图7（b）中可见150循环后发动机剩余寿命预测的PDF曲线，每条PDF曲线均包含了发动机真实剩余寿命，且随着运行时间的增加预测剩余寿命和真实剩余寿命逐渐靠近（如图8所示），意味着对发动机剩余寿命预测的不确定性逐渐减弱。此外，在每个监测点模型参数会根据退化数据的增加自适应地估计和在线更新，因此，所得到的PDF曲线逐渐变窄而尖锐，说明了本文方法可以更好地预测发动机的剩余寿命。

从图8中可见，随着监测数据的积累，黑线越来越贴近红线，剩余寿命预测的精度逐渐提高，并且根据图7的概率密度函数，可以计算发动机剩余寿命预测的均方误差，如图9所示。从图中可见，随着时间的推移，剩余寿命预测的均方误差越来越小，剩余寿命的预测精度逐渐提高。

图8 剩余寿命预测值与真实值对比

图9 均方误差

为了进一步证明本文方法的优越性，与一种由标准布朗运动驱动的线性Wiener过程预测发动机剩余寿命的方法进行对比。2种方法在所有监测点的预测剩余寿命与真实剩余寿命的比较结果如图10所示。从图中可见，线性方法在发动机运行早期的预测结果并不理想，在运行后期的剩余寿命预测具有一定的参考性；而本文方法在发动机运行早期就可以为判断发动机健康状态提供一定的依据，在发动机运行全过程中，预测结果逐渐向真实剩余寿命靠近，具有较强的预测能力，剩余寿命预测精度更高。