特征模分析在电磁场与微波技术教学中的应用
2022-10-12刘双兵
刘双兵
(巢湖学院 电子工程学院,安徽 合肥 238024)
2018年11月24日,吴岩在第十一届“中国大学教学论坛”上做“建设中国金课”的报告,首次提出以高阶性、创新性和挑战度为内涵的“金课”建设标准[1]。高阶性,是指知识、能力、素质有机融合,培养学生解决复杂问题的综合能力和高级思维;创新性,是指课程内容反映前沿性和时代性、教学形式体现先进性和互动性、学习结果具有探究性和个性化;挑战度,是指课程要有一定难度,需要学生和教师一起跳一跳才能够得着,教师备课和学生课下有较高要求。高校教师要抓住一流课程建设机遇,转变教学观念和形式,积极探索新思路,提高课程“两性一度”内涵,通过课程质量的提升推动本科教学高质量发展[2]。
电磁场与微波技术是电子信息与通信类专业的专业基础课,内容包括电磁场与电磁波基本知识、微波技术基础和天线与电波传播三大部分,既具有较强的理论性,又具有广泛的工程应用性。为了丰富教学内容和教学手段,提高教学效果,一些高校教师针对电磁场与微波技术课程教学开展了教学研究与改革探索。为了培养学生微波工程的实践动手和创新设计能力,陈晓辉等人[3]以波导双孔定向耦合器和多螺钉极化转换器为教学案例,将电磁仿真软件引入课程教学。为了增强学生解决复杂工程问题的能力,邢蕾等人[4]采用介质谐振天线设计案例,将理论分析与电磁仿真结合的微波器件设计应用于教学。朱浩然等人[5]提出一种场路结合的仿真教学方法。为培养学生创新意识、用科研方法解决复杂工程问题的能力,刘北佳等人[6]提出了电磁仿真与加工测试结合的可重构天线创新实验教学模式。为了将电磁理论知识形象化,提升学生对实际问题的分析能力,潘柏操[7]在课程教学中采用色散特性的电磁仿真方法。这些措施在一定程度上丰富了课程教学方法,提高了学生的知识应用和解决工程问题的能力,使课程具有一定挑战度,其不足之处在于电磁理论知识深度的挖掘不够,未能体现课程的高阶性和创新性。
1965年,文献[8]首次提出特征模式理论,并将其应用于任意形状金属导体散射问题的模式分析。1971年,文献[9]在电场积分方程基础上重新建立了金属导体的特征模理论,为其在今后的发展和应用奠定了坚实的基础。近年来,特征模理论[10]被广泛应用于各种新型天线设计中,如可重构天线及滤波天线[11]、多进多出(MIMO)手机天线[12]、超表面天线[13-14]、5G圆极化天线[15]、低剖面单极子天线[16]等,在天线领域具有非常重要的地位和作用。特征模分析以电磁场基本方程为基础,应用矩量法求解金属导体的电磁辐射与散射问题,得到任意形状导体结构的各种可能谐振模式、模式电流分布及其远场辐射方向图,有助于通过馈电结构与位置设计以实现各类高性能天线设计。借助特征模分析,适当扩展课程知识难度,一定程度上开发课程深度,开展个性化天线设计以提升课程挑战度,可以构建出具有“两性一度”特性的一流本科课程。
1 特征模理论
1.1 空间电磁场的求解
在均匀媒质中,时谐电磁场满足频域Maxwell方程组:


(1)式和(2)式是电磁场基本方程,是解决电磁问题的根本出发点。应用该方程求解电磁场问题时,通常引入


其中k=ω με为电磁波波数。
根据Green定理,(3)式中第一个方程在直角坐标系下的解可表示为:

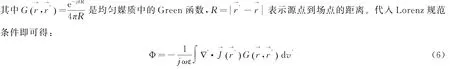
将(5)式和(6)式代入(3)式中的第二个表达式,就可得到空间电场的唯一解,结合Maxwell方程可进一步得到磁场的解。
1.2 电场积分方程的推导


式中μ0是自由空间磁导率,ε0是自由空间介电常数。引入算子L在感应电流与散射场之间建立联系,即
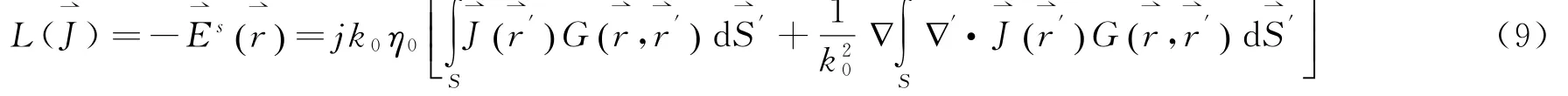
式中k0是自由空间波数,η0是自由空间波阻抗。代入(7)式可得电场积分方程:

1.3 特征模理论
利用矩量法对电场积分方程进行求解即可得到理想导体特征模理论。其求解思想是利用矩量法中的展开函数和测试函数得到导体上电流的模态解,即是模式电流的线性叠加,同时电场和磁场与电流呈线性相关,从而也可以用模态形式表示。在特征模理论中,仅需已知天线结构,而不考虑激励或入射场,也就是说分析出该结构形状和材料有关的所有固有模式,从而洞察结构本身的固有电磁特性。
将具有正交性的模式电流作为基函数,则可得到理想导体表面电流的表达式:


其中λn是特征值是模态激发系数。定义模式重要性:

即模式电流的归一化振幅,表征模式的储能和谐振状态,其变化区间为0<MS≤1。当MS=1时,则该模式处于谐振状态;而MS接近于0时,则体现为储能状态。另外,特征角也能反映出模式状态,其定义为:

很显然,特征角的取值范围为90°<βn<270°。当90°<βn<180°时,表示该模式处于感性模式状态,存储磁能;当180°<βn<270°时,则该模式处于容性状态,储存电能。特征模三个重要系数之间的关系总结如表1所示:

表1 特征模的三个系数之间的关系
2 基于特征模分析的圆极化贴片天线设计
2.1 带有U型缝隙贴片的特征模分析
贴片天线在无线通信系统中应用十分广泛,圆极化贴片天线的传统设计方法是在理论公式基础上对结构参数进行优化分析,通常耗时费力。应用特征模分析可以得到贴片结构产生圆极化辐射的物理机制,为圆极化贴片天线的馈电结构设计和性能提高提供了清晰的设计思路,本文以蚀刻U型缝隙贴片的特征模分析来阐述这一过程。
带有非对称U型缝隙的方形贴片结构如图1所示,放置在相对介电常数为εr=1.1、厚度为11 mm的泡沫衬底的表面,几何尺寸分别为:l=44.7 mm,l1=28.2 mm,l2=16.9 mm,l3=21.8 mm,w=2.3 mm,方形贴片和接地面均采用厚度为0.5 mm的铜箔构成。应用电磁仿真软件对该结构进行特征模分析,得到2 GHz附近前两个特征模的模式重要性(MS)和特征角如图2所示,该两个模式在2.19 GHz频率处对应的表面电流分布和辐射方向图如图3所示。
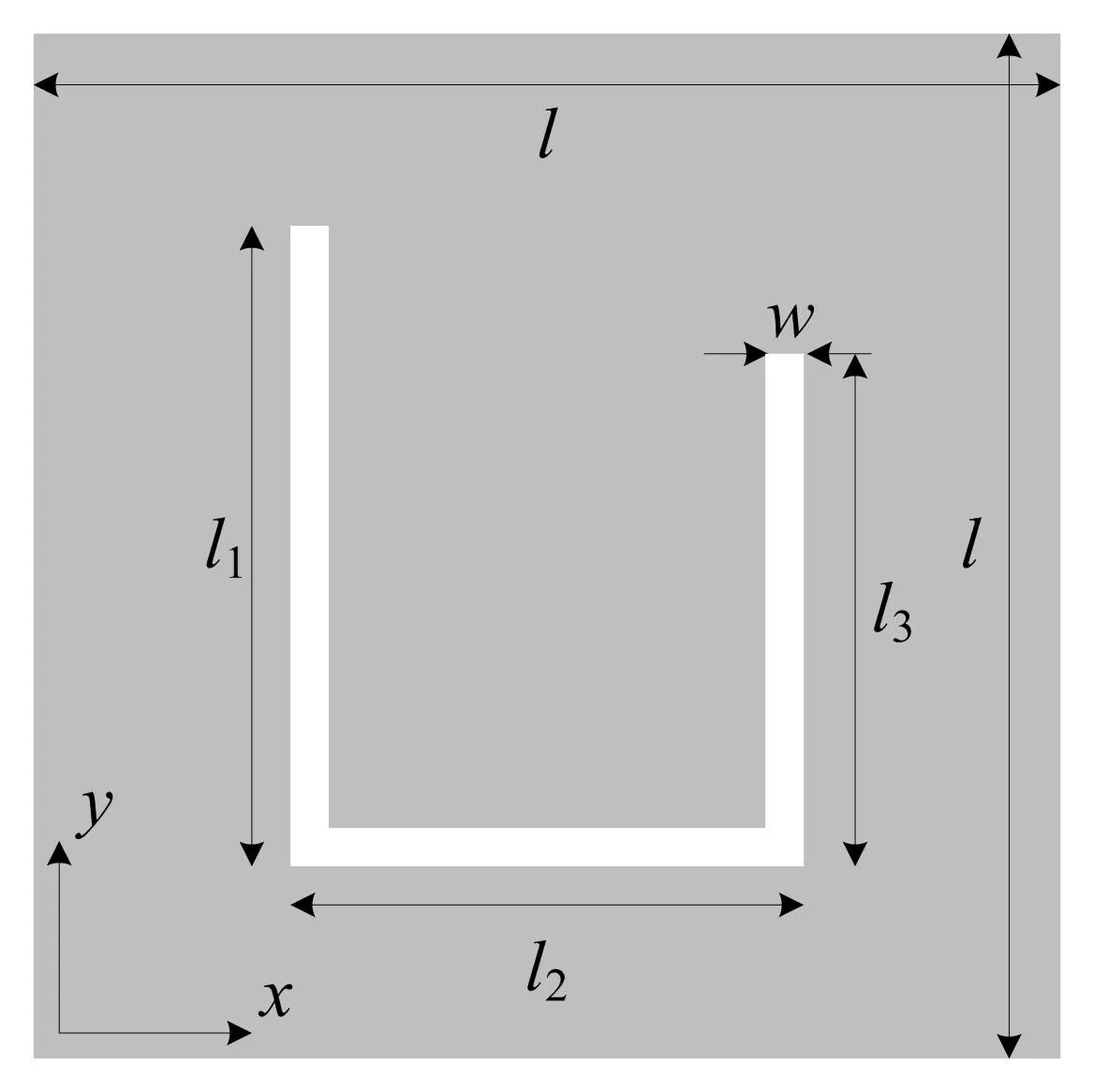
图1 带有U型缝隙的方形贴片
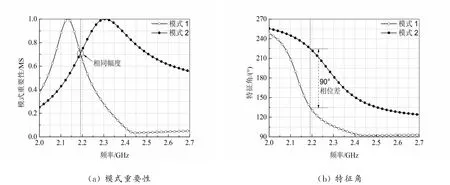
图2 U型缝隙贴片的前两个特征模式
由图2可见,两种模式在2.19 GHz时具有完全相同的电流振幅和90°的相位差。而图3表明,模式J1为垂直极化模式,表面电流主要集中在U型槽的长臂末端;而模式J2为水平极化模式,表面电流主要分布在U型槽短臂的末端,且由图3(c)和(d)可以看出,两种模式均在方形贴片的正上方即在+z方向产生辐射。因此,如果这两个正交特征模式可以同时被激发,就可以得到一个圆极化天线。

图3 两个特征模式的表面电流分布和辐射方向图
2.2 圆极化U型槽贴片天线
采用同轴探针对带有U型槽的贴片进行馈电,构成贴片天线。为了同时激励起特征模J1和J2,需要选取两个模式表面电流分布振幅较强且方向一致的位置进行馈电。通过对比图3(a)和3(b)可以发现,在U型槽的长臂末端区域,模式J1和J2的表面电流分布均较强,且方向完全一致。因此,该区域是最佳的探针馈电位置,得到的贴片天线结构如图4所示,其中l4=16.9 mm,d=5 mm。应用电磁仿真软件对该天线进行分析,得到其回波损耗、轴比和远场辐射方向图分别如图5、图6、图7所示。
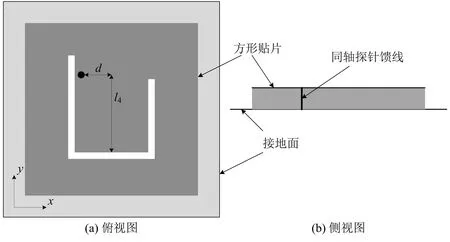
图4 贴片天线结构示意图
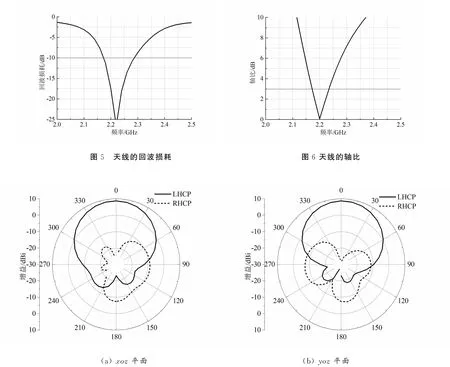
图7 天线在2.2 GHz处的远场辐射方向图
由图5可知,天线在2.22 GHz处产生了谐振,-10 dB阻抗带宽为0.1 GHz(2.18~2.28 GHz)。图6和图7表明,天线在2.2 GHz的轴比为0.06 dB,在xoz和yoz平面形成明显的左旋圆极化(LHCP)辐射,且在其侧向(+z)产生了8.7 dBi的辐射增益。该仿真结果充分表明:利用该探针馈电,有效激励了U型槽方形贴片的J1和J2特征模,且J2模(+x方向极化)的特征角滞后J1模(+y方向极化)的特征角90°,从而形成左旋圆极化辐射。
3 基于特征模分析的课程教学实践
通过以上对特征模理论和特征模分析在贴片天线设计中的应用案例的阐述,可以得出结论:特征模分析是对电磁基本理论的深化,也为天线设计这一工程问题提供清晰的物理内涵洞悉和创新思维,这与电磁场与微波技术课程兼具理论性和实践性的特征十分吻合,因此特征模分析可以贯穿于整个课程教学过程。
通常采取以下三个阶梯递进式开展课程教学实践:第一,理论知识进阶层次。在讲解电磁场与电磁波知识后,要求学生自主学习矩量法,并推导出电场积分方程和特征模理论。这将有助于学生熟练掌握矢量运算、Maxwell方程组的物理意义、电磁场边界条件等电磁场基本知识,同时提升知识深度。第二,天线发展现状调研。在讲解微波技术基础和天线基本理论知识的同时,要求学生分组开展新型天线研究现状调研,并形成调研报告,在课堂进行调研成果分享交流。这将有助于学生了解学科前沿,促进学生个性化发展,同时丰富教学手段和教学方法。第三,基于特征模分析的新型天线设计。要求学生结合调研主题和结果,自主选择天线结构,在特征模分析基础上,细致分析特征模的电流分布、特征角和模式辐射特性,完成具有某种特性的天线设计。这将要求学生针对一些具体工程问题进行探索,培养学生工程应用和实践创新能力。总之,将特征模分析应用于电磁场与微波技术课程教学,从教学目标、教学内容、教学设计、教学方法与手段、教学考核等多角度提高课程的高阶性、创新性和挑战度。
4 结语
在一流本科课程建设背景下,我们以“两性一度”为标准开展电磁场与微波技术课程教学研究与改革探索,从电磁场基本方程出发,推导了特征模理论;概述了基于特征模分析的圆极化贴片天线设计案例,体现了特征模分析在天线领域的有效性和重要性;以三个阶梯递进层次阐明了特征模分析在课程教学中的应用性。结果表明,将特征模分析贯穿于整个课程教学中,既强调电磁场基本理论的深入,又强化学生工程应用与实践创新能力培养,促进了课程内涵建设,提升了教学质量和效果。
