致密砂岩储层岩石物理模型应用分析

张恒铁

(中煤地质集团有限公司，北京 100040)

0 引言

地震岩石物理作为地球物理学的一个重要分支，主要研究的是岩石的物理性质与地震响应之间的关系，是储层物性参数和储层弹性参数之间的桥梁。目前已经勘探和开发的各大油田，大多数是都是孔隙度大、渗透率高的储层，而对低孔低渗储层的认识较为欠缺。随着勘探和钻井技术的提高，现在已经开始致力于寻找非常规的致密砂岩储层。致密砂岩裂缝型储层的地震岩石物理建模方法研究，在致密油气中的勘探就显得尤为重要。

致密砂岩储层具有低孔隙度、低渗透率、岩性致密、圈闭幅度低、气藏压力系数低、自然产能率低等特征[1-2]。目前国内比较认可的概念是把孔隙度小于10%，渗透率小于0.1mD的砂岩储层称为致密砂岩储层[3]。地震岩石物理研究是建立岩石物理性质和油藏基本参数之间关系的主要途径，在地震数据处理、岩石物理参数获取、定量化解释和风险评估等环节发挥重要作用，可有效提高地震岩性识别、储层预测与流体检测的精度和可靠性。前人对致密砂岩的岩石物理研究也做了很多工作，Rojas(2005)分析了致密砂岩中的压力、孔隙流体和岩性变化等对纵横波速度比的影响[4-5]；Smith、Sayers等(2009)深入探讨了低孔低渗砂岩中岩石性质，并指出致密砂岩中纵横波速度与孔隙度的相关性不大[6-7]； Ruiz等(2011)提出了两种用于估算致密砂岩弹性模量的岩石物理模型，即：软孔隙度模型(SPM)和单一纵横比模型(SAR)，将用于实际工区的致密砂岩储层的横波速度进行计算和分析，取得了较好的效果[8-10]；唐晓明(2011)通过对Biot理论的推广，考虑了岩石裂隙的挤喷流效应，提出了裂隙孔隙模型[11-12]；印兴耀(2013)提出基于Biot相洽理论的致密砂岩弹性参数计算方法[13]。

本文重点讨论Ruiz等两种适用于致密砂岩的岩石物理模型，即软孔隙度模型(SPM)和单一纵横比模型(SAR)。软孔隙度模型(SPM)将致密砂岩看作是连续的岩石基质中嵌入了球状孔隙(硬孔隙)和裂隙状孔隙(软孔隙)；单一纵横比模型(SAR)假设岩石中所有的孔隙具有相同的孔隙纵横比[14-15]；这两个模型的优点是用一个单一的岩石物理参数来估算复杂的多矿物岩石的弹性性质，适用于低孔低渗岩石中的各种流体替换情况[16-17]。

1 方法原理

1.1 Hashin-Strikman求岩石基质的弹性模量

通过致密砂岩中各组成成分的体积含量和弹性模量，用理论方法估算矿物颗粒和孔隙中混合物的等效弹性模量。Hashin和Shtrikamn根据变分原理推导出由双相介质构成的弹性复合介质最严格的、最可能窄的弹性模量上下限：

(1)

(2)

式中：K1、K2分别表示岩石各组分的体积模量；μ1，μ2分别表示岩石各组分的剪切模量；f1，f2分别表示岩石各组分的体积分数。一般来说，当下标1表示刚性较大的组分时，上述表达式求得上限；当下标2表示刚性较大的组分时，求得下限。

更一般的多矿物Hashin-Shtrikman上下限公式如下：

(3)

KHS+=Λ(μmax),KHS-=Λ(μmin)

(4)

μHS+=Γ(ζ(Kmax,μmax)),μHS-=Γ(ζ(Kmin,μmin))

(5)

(6)

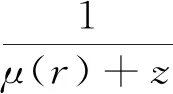
(7)

(8)

〈·〉表示对材料的平均，即对各成分按其体积含量求加权平均。

1.2 自相容近似求流体饱和岩石的弹性模量

Berryman(1980，1995)给出了N相混合物的自相容近似的一般形式：

(9)

(10)

1.3 软孔隙度模型(SPM)的基本原理

软孔隙度模型(SPM)是指在特定的测井深度范围内，软孔隙度模型将岩石的总孔隙度(φTotal)分为两部分：硬孔隙空间(硬孔隙度)和软孔隙空间(软孔隙度)。软孔隙度(φsoft)是指孔隙纵横比α=0.01的扁平球状包含物的体积分数，硬孔隙度(φstiff)是指孔隙纵横比α=1的球状包含物的体积分数。即：

φTotal=φstiff(α=1)+φsoft(α=0.01)

(11)

图1 软孔隙度模型(SPM)中孔隙的分布

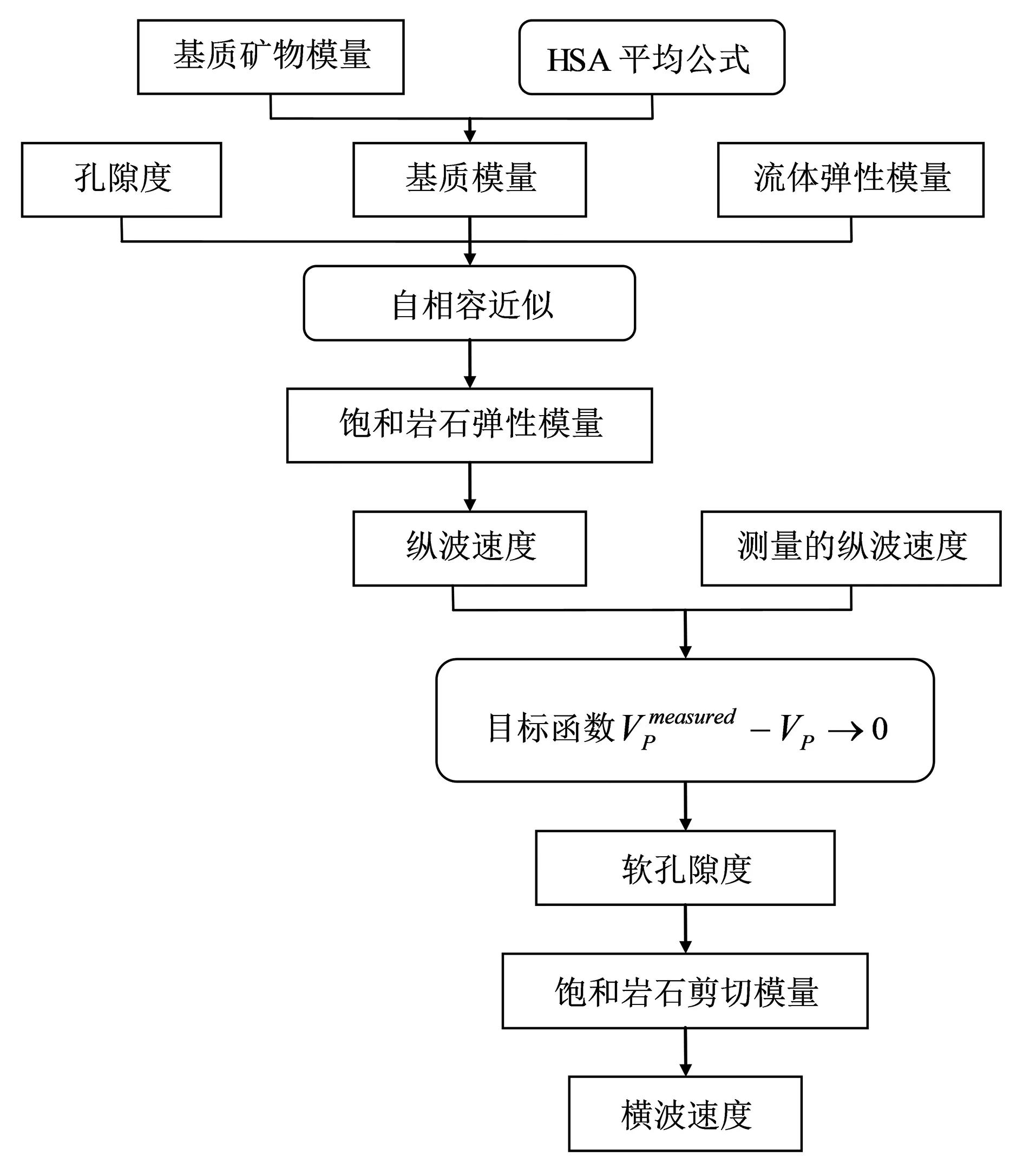
图2 软孔隙度模型(SPM)横波速度预测流程

根据以上流程(图2)求取软孔隙度φsoft的主要步骤如下：①利用多矿物的Hashin-Strikman上下限平均公式估算岩石基质的弹性模量；②用Berryman的自相容模型(SC)将包含物和孔隙流体添加到岩石基质中，求取饱和岩石的等效弹性模量；③利用测井所得的纵波速度进行约束，从而反演出致密砂岩中的软孔隙度；④根据反演出的软孔隙度，结合自相容近似，对流体饱和岩石的等效弹性模量进行修正，从而进行横波速度的预测。

1.4 单一纵横比模型(SAR)的基本原理

与软孔隙度模型(SPM)类似，单一纵横比模型(SAR)是由Ruiz等提出来用于估算致密岩石的弹性模量[8-10]。SAR假设岩石在特定的深度范围内，岩石中所有的孔隙都是由扁平球状孔隙组成，并且具有相同的纵横比。所有孔隙纵横比αSAR是深度z的函数，即：αSAR=αSAR(z)。其孔隙在岩石中的空间分布如图3所示；单一纵横比模型(SAR)实现步骤如图4所示。

图3 单一纵横比模型(SAR)中孔隙的分布

图4 单一纵横比模型(SAR)横波速度预测流程

根据以上流程(图4)求取致密砂岩中的单一纵横比αSAR的主要步骤如下：①假设岩石中所有的孔隙具有相同的孔隙纵横比，并任意给定一个初值；②利用多矿物的Hashin-Strikman上下限的平均公式来估算岩石基质的弹性模量；③根据自相容模型求出饱和岩石的等效弹性模量，并估算出纵波速度，根据测井所得的纵波速度约束估算的纵波速度，从而反演出岩石孔隙中的单一纵横比；④根据反演出的单一纵横比，结合自相容模型，重新计算饱和岩石的等效弹性模量，达到横波预测的目的。

2 实际资料计算

选取某工区的致密井资料，该致密砂岩井段的孔隙度较低，整体小于10%。由于砂岩的致密性，纵横波速度相比于普通的砂泥岩地层大(图5)。

2.1 SPM模型预测横波速度

采用SPM模型的实现流程，假设岩石基质中只含有石英和泥质两种矿物，可以估算纵波速度，用测井所得的纵波速度约束所预测的纵波。得到的理论计算的纵横波速度与测井实测的纵横波速度及其相对误差如图6所示。

由图6可知，纵波的测量值与预测值吻合较好，纵波的大部分点都在2%以内，极少数点在4%之内，基本上符合了实际资料的要求。横波的测量值与预测值大体趋势基本相同，一致性较好，且横波的相对误差控制在5%左右，以上表明SPM模型预测所得的横波资料可信度较高。

图5 某工区致密砂岩储层的测井曲线

图6 软孔隙度模型(SPM)的纵横波速度预测及其相对误差

2.2 SAR模型预测横波速度

根据SAR模型的实现流程，假设岩石中所有的孔隙具有相同的孔隙纵横比，可估算得到纵波速度，并用测井所得的纵波速度来约束所预测的纵波。预测的纵横波速度与测井实测的纵横波速度及其相对误差如图7所示。

由图7可知，由于纵波速度估算值被测井值所约束，所以纵波速度的测量值与估算值吻合较好，两者之间的相对误差控制在2%以内。横波速度的估算值与测量值大体趋势基本相同，两者之间的相对误差基本控制在5%左右，部分点在10%以内，基本上符合实际资料所达的精度范围。

图7 单一纵横比模型(SAR)的纵横波速度预测及其相对误差

3 结论

在岩石物理基础上，通过对致密砂岩的两个岩石物理模型计算和实例分析，得出以下结论：

1)通过对SPM模型的应用分析，结果表明SPM模型对实际的致密砂岩测井资料能取得较好的效果，模型最大的优点是可用单一的微观岩石物理参数来估算复杂的多矿物岩石的弹性性质。

2)通过对两种模型的比较，得出SPM模型和SAR模型应用于致密砂岩的横波预测能获得较好的效果，但是SPM模型的预测精度比SAR模型略高一些。