离港航班滑出时间的支持向量机预测模型

2022-10-12夏正洪贾鑫磊

科学技术与工程 2022年25期

夏正洪，贾鑫磊

(中国民航飞行学院空中交通管理学院，广汉 618307)

滑出时间指从停机位开始滑出到实际起飞的时间间隔，是体现机场运行效率的重要指标。随着航班流量的快速增加，场面平均滑行时间也在随之增大，严重影响了机场场面运行效率。因此，准确预测航班起飞前的滑出时间，对于提高机场运行效率、优化航班起飞顺序，改善机场场面的交通状况有重要意义。

目前，国外关于离港航班滑出时间预测的研究已较为成熟。Lee等[1]利用机器学习算法来预测滑出时间，预测效果良好。George等[2]基于航班历史数据对离港航班的滑出时间进行了动态预测，提出了基于强化学习的Q-Learning方法，且预测精度较高。Herrema等[3]基于历史数据对单跑道场面滑行时间进行了预测。 Balakrishna等[4]基于随机动态规划理论建立了多跑道非参数强化学习滑出时间模型，可得到精度较高的预测结果。 Simaiakis等[5]利用自主研发的排队系统来预测场面交通拥堵情况，预测精度非常显著。

国内关于离港航班滑出时间的预测研究还处于起步阶段。刘家学等[6]提出差分自回归移动平均(autoregressive integrated moving average model，ARIMA)模型与支持向量回归模型组合的预测模型，可将滑出时间的预测精度提升至90%。冯霞等[7]构建了基于K最近邻(K-nearest neighbor，KNN)和支持向量回归(support vector regression，SVR)的离港航班滑出时间预测模型，误差范围为±3 min内的预测准确率可达到79.86%。邢志伟等[8]利用贝叶斯网的增量学习特点对预测模型进行动态调整，从而使模型能够动态地估计离港航班滑行时间。周建等[9]提出了改进的畅通滑出时间预测算法，使得重型机和中型机畅通滑出时间误差范围在±3 min内的预测准确率分别达到94.12%和100%。刘继新等[10]提出了基于SVR和反向传播(back propagation，BP)神经网络的离港滑行时间预测模型，并将预测结果用于A-CDM系统中，有效地提升了机场场面的运行效率。冯霞等[11]基于单跑道建立了无障碍滑出时间的计算模型与基于排队论的等待起飞时间预测模型。李楠等[12]根据分类结果建立多元回归模型，相较于传统多元线性回归，机器学习交叉训练集下的预测准确度更高。陈祯等[13]从特征选择的角度对滑出时间预测模型改进，相比于单一特征，引入交互特征可以提高准确率。董兵[14]提出了冲突点选择避让机制来优化航空器滑行路径。建立了路径滑行优化模型。经算法优化后，可减少时间段内各航班的最短滑行路径的冲突，缩短滑行时间。向征等[15]提出基于管制移交间隔优化离港航班时刻的模型，可使离港航班在出港点处建立符合移交条件的间隔，有效降低因不满足移交间隔造成的飞行冲突，提高航班流的有序性。

综上所述，现有研究成果多以单跑道机场或多跑道机场中的一条跑道为研究对象，忽略了跑滑系统结构及场面交通流对滑出时间的影响。同时，已有成果对滑出时间影响因素的相关性并未进行深入分析，导致所构建模型得出的滑出时间预测结果与实际滑出时间偏差较大。因此，现首先分析影响离港航班滑出时间的可量化因素，并构建基于相关性分析结果的滑出时间预测模型；基于中国中南某H型双跑道枢纽机场2周实际运行数据，分别采用SVM和BP神经网络对滑出时间进行预测，以期获得更准确的滑出时间预测效果。

1 滑出时间影响因素及相关性分析

1.1 影响因素

滑出时间等于离港航班的实际起飞时间减去实际撤轮档时间，表达式为

TA=T1-T2

(1)

式(1)中：TA为离港航班的实际滑出时间；T1为实际起飞时刻；T2为实际撤轮档时刻。

根据离港航班的管制指挥过程可知，离港航班停机位远近、机场的高峰时段、地面交通流量、航班的滑行速度、是否为直线滑行、经过多少个弯道等因素都会影响航班的滑行时间。其中，机场地面交通流对滑出时间的影响非常显著，如同时段进港航班和离港航班越多，则对后续离港航班的滑出时间影响越大，且很容易造成滑行冲突，从而增加离港航班的滑出时间。此外，天气、流量控制、跑道构型等对滑出时间都有一定的影响，但由于很难量化这些因素，故不做讨论。因此，提出了8个可以量化的影响因素：同时段推出航班数量x1、同时段起飞航班数量x2、同时段内进港航班数量x3、1 h内平均滑出时间x4、滑行距离x5、转弯转角个数x6、延误x7、离港航班起飞时刻所在的时段x8。

(1)同时段推出航班数量x1。同时段推出的航班数量x1(i)即在满足推出时刻处于某航班i撤轮档时刻tBlock-out到起飞时刻tTake-off之间的航班Sj1的数量。

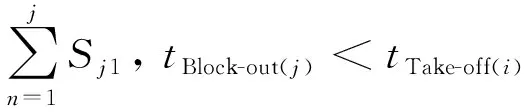
tBlock-out(j)>tBlock-out(i)

(2)

(2)同时段起飞航班数量x2。同时段起飞航班数量x2(i)即满足起飞时刻处于某航班i撤轮档时刻到起飞时刻之间的航班Sj2的数量。

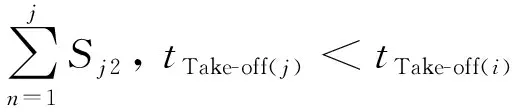
tTake-off(j)>tBlock-out(i)

(3)

(3)同时段进港航班数量x3。同时段进港航班数量x3(i)即满足落地时刻tArrive处于某航班i撤轮档时刻到起飞时刻之间的航班Sj3的数量。

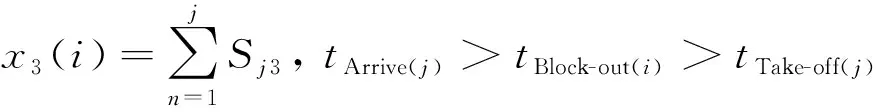
(4)

(4)1 h内平均滑出时间x4。1 h平均滑出时间x4即在某1 h内所有航空的实际滑出时间的平均值。

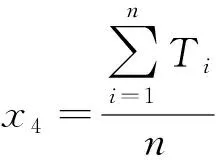
(5)

式(5)中：Ti为第i架航班的实际滑出时间。

(5)滑行距离x5。滑行距离x5表示滑行路径的总长度da与跑道长度db的比值乘以3 600。

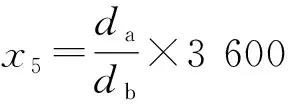
(6)

(6)转弯转角个数x6。航班直线滑行速度与转弯滑行速度有较大的差异，因此离港航班在滑出过程中如果经历的转弯个数越多，则其滑行时间会增加[8]。

(7)延误x7。根据交通流的传播特性，延误可能出现累积和传播现象；即上1 h的延误可能会对后续航班的滑出时间造成影响。根据《中国民用航空空中交通管理规则》可知：当实际起飞时间大于预计起飞时间15 min时，则开始计算延误，反之则延误为0。

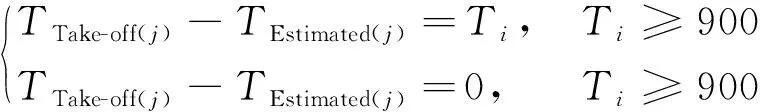
(7)

式(7)中：TEstimated(j)表示上1 h离港航班j的预计起飞时间；TTake-off(j)表示上1 h离港航班j的实际起飞时间；900表示以秒为单位的延误阈值。

(8)离港航班起飞时刻所在时段x8。大型机场的地面交通流通常呈现明显的日变化特征，即存在明显的早高峰、午间高峰和晚高峰，这些高峰小时的平均滑出时间通常较长。因此，引入航班起飞时刻所在的时段这个可量化的因素，将1 d按1 h划分为24个时段，取数值1～24作为航班所在时段，用于区分高峰小时和正常时间段。

1.2 数据整理

所用数据来源于中国中南某机场2周的实际运行数据，主要包含航班号、机型、实际起飞时间、撤轮挡时间、实际落地时间、跑道号和停机位等信息。将原始数据中异常数据进行筛查和清理，包括同一时间重复记录的数据、滑出时间超过60 min的异常数据等。根据式(1)～式(7)依次计算出模型所需数据，得到滑出时间预测所需数据集如表1所示。

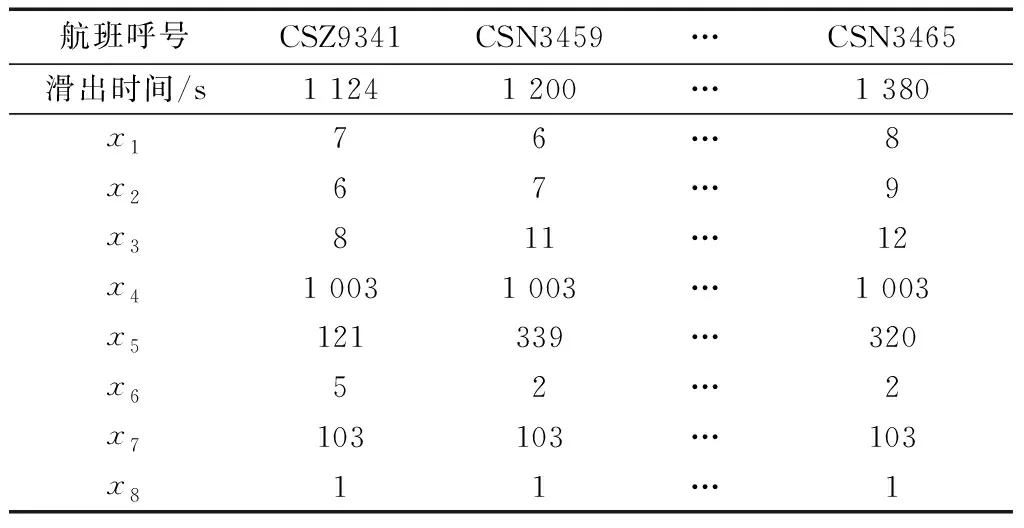
表1 整理后的数据集

1.3 相关性分析

将整理后的数据集导入SPSS软件中，可得到各个影响因素与实际滑出时间的相关性分析结果如表2所示。

表2 相关性分析结果

皮尔逊相关性系数越接近1表示相关性越强，检验级别表示相关性的显著程度，由表2可得以下结论：同时段推出航班数量、同时段起飞航班数量、同时段进港航班数量、1 h平均滑出时间与离港航班的滑出时间显著相关，滑行距离、转弯个数、延误与滑出时间相关但不显著(中度相关性)，离港航班所在时段与滑出时间不相关。

2 基于SVM的离港航班滑出时间预测模型

2.1 SVM算法原理

支持向量机(SVM)是一种监督式学习的方法，它广泛应用于统计分类以及回归分析中。SVM的优点在于可高效处理并简化高维特征空间的分类问题，并且在实际应用的分类问题中可以通过灵活运用核函数来生成不同的非线性决策边界，从而保证SVM可以在不同的问题上都有出色的表现[14]。

支持向量机可分为线性和非线性两大类。所建立的模型是非线性支持向量机预测模型，其本质是非线性核函数将xi映射到高维空间后寻找最优解即最优超平面。

wφ(x)+b=0

(8)

式(8)中：w为法向量；φ(x)为非线性核函数；x为特征向量；b为偏置项。

根据结构风险最小化原则，求解参数w和b需建立的目标函数及约束条件如下。

(9)

式(9)中：C为惩罚因子；n为样本数量；φi为非负松弛变量。

现有的各类核函数中，高斯径向基函数(radial basis function, RBF) 具有设置参数少、计算复杂度低等特点[15]，故采用RBF函数作为SVM的核函数，即

(10)

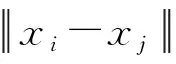
2.2 基于相关性分析的滑出时间预测模型

不同影响因素与滑出时间的相关性不同，相关性越强则说明对滑出时间的影响越大。为讨论影响因素的相关性强弱对模型预测精度的影响，构建了不同维数的滑出时间SVM预测模型，如图1所示，根据相关性强弱分为包含仅考虑显著相关因素的四元组合、考虑显著相关和中度相关因素的七元组合以及综合考虑所有可量化影响因素的八元组合。

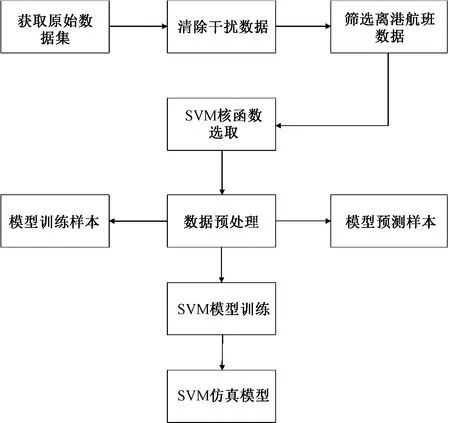
图1 基于SVM的滑出时间预测流程图Fig.1 SVM-based taxi-time time prediction flow chart

基于SVM的离港航班滑出时间预测流程如下。

步骤1筛选：删除有明显错误的数据，如滑出时间过长或过短、数据重复等。错误数据会影响整个模型精度，偏离实际，以致结果误差过大。

步骤2数据预处理：根据式(1)～式(7)求得滑出时间预测所需的输入参数。

步骤3选取模型特征及对应的RBF函数作为SVM的核函数。

步骤4将数据集进行归一化处理，得到实验数据集，并划分5500组数据为训练集与419组数据为测试集。

步骤5在训练集采用网格搜索法和交叉验证确定SVM的最优参数组合c和g，并完成模型的构建。

步骤6训练模型并利用测试集计算各个误差及准确率，评价模型性能。

3 案例分析

以中国中南某枢纽机场作为研究对象，该机场属于典型的H形跑滑系统结构，运行方式可采用隔离运行或者相关平行进近。基于该机场2019年5月26日—6月8日共计2周的实际运行数据12 323条，其中包含离港航班和进港航班分别为5 690架次和6 633架次。通过对原始数据进行处理，得到可用训练数据集5 500条和测试集419条，并对离港航班的历史滑出时间分布进行聚类分析，结果如图2所示。

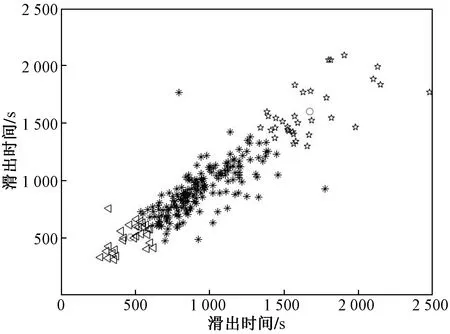
图2 滑出时间聚类分析结果Fig.2 Clustering analysis results of taxi-out time

由图2可知，该机场离港航班实际滑出时间在0～600 s占5%，600～900 s占9%，900～1 500 s占62%，1 500～2 500 s占23%，2 500 s以上占1%。可见，该机场的实际滑出时间主要分布在900～1 500 s，滑出时间超过900 s(15 min)占比约为86%，说明该机场场面运行效率较低。因此，需要通过科学方法，准确预测离港航班的滑出时间，从而更为精准地控制其推出开车时间，减少滑行冲突，缩短离港航班的滑出时间，提升机场场面运行效率。

3.1 SVM模型预测结果分析

模型参数c和g对SVM的分类结果具有很大影响。在采用RBF函数作为SVM核函数，采用网格搜索算法确定c和核函数参数g的最优值。选取K=10作为交叉验证的次数，并限定参数c和g的变化范围为[0.1,10]，网格搜索步长为0.1。将样本数据的顺序打乱，采用随机数据集进行训练，可得四组、七组和八组的预测结果对比及分析如图3、表3所示。

对比七元组和四元组的预测结果可知，在加入中度相关的因素后，平均绝对百分比误差(mean absolute percentage error，MAPE)提升了1.3%，平均绝对误差(mean absolute error，MAE)和均方根误差(root mean squared error，RMSE)分别减少了35.796 8 s和43.888 1 s，±3 min和±5 min的准确率分别提升了1.9%和3.9%。对比七元组和八元组预测结果可知，加入不相关的可量化因素后，MAPE下降了1.4%，MAE和RMSE分别增加了17.960 4和35.486 37，±3 min和±5 min的准确率分别下降了0.6%和2.0%。可见，考虑强相关性、中度相关性的七元组合预测模型的性能最佳：仅为0.118 6，MAE为92.267 4 s，RMSE为120.587 8 s，预测结果±3 min内的准确率为89.5%，±5 min内的准确率98.0%。

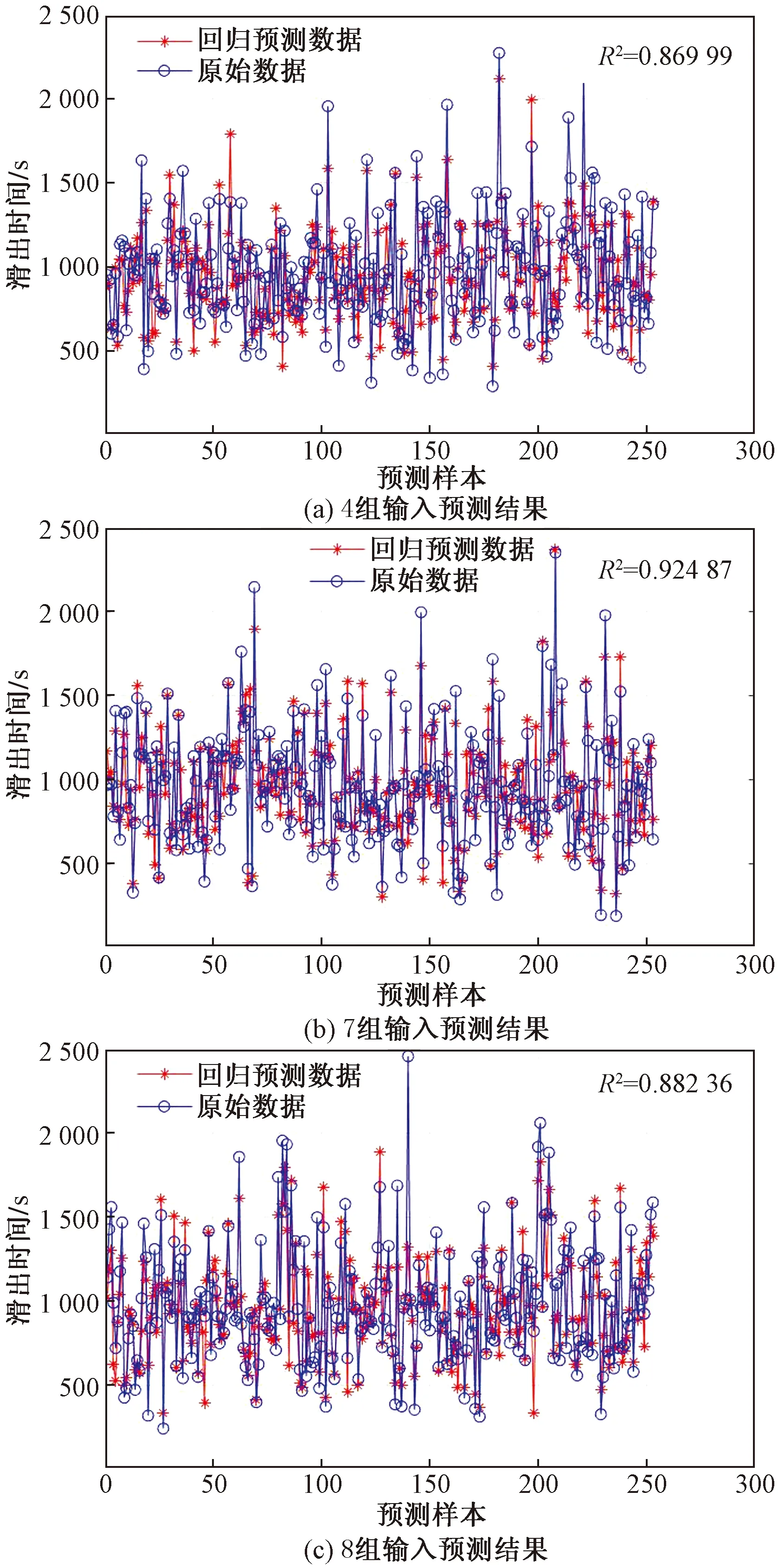
图3 基于SVM的离港航班滑出时间预测结果Fig.3 Prediction results of taxi-out time based on SVM

3.2 SVM与BP神经网络模型预测结果对比分析

为保证预测结果对比的公平性，选用同样的训练集和测试集，利用MATLAB中的BP神经网络工具箱进行编程，分别得到显著相关的四组数据、加入中度相关性的七组数据以及全部可量化因素的八组影响数据结果。SVM预测模型与BP神经网络预测模型的结果对比如表4所示。

表4 SVM预测与BP神经网络对比

经对比可知：基于SVM和BP神经网络的预测结果趋势是一致的，仅考虑强相关因素的四元组效果相对较差；引入中度相关影响因素之后，七元组预测结果准确率达到最佳；若再加入弱相关或不相关的影响因素，八元组预测的准确率会有明显的下降。对比BP神经网络和SVM预测模型的四元组、七元组可知，SVM预测模型的预测结果较BP神经网络预测结果在MAPE提升了4.49%，MAE和RMSE分别下降了17.386 1 s和30.666 7 s，±3 min和±5 min的准确率分别提升了5.3%和1.6%。以上数据证明了SVM模型预测结果明显优于BP神经网络，更适合应用于离港航班的滑出时间预测中。考虑七组可量化数据的SVM预测模型预测性能最佳：平均绝对误差百分比MAPE为0.118 6，MAE为92.267 4 s，RMSE为120.587 8 s，预测结果±3 min内的准确率为89.5%，±5 min内的准确率为98.0%。