基于正交实验法射孔参数优化设计数值模拟

幸雪松， 邱浩*， 文敏， 侯泽宁， 黄辉， 毕刚

(1.中海油研究总院有限责任公司， 北京 100028； 2.西安石油大学石油工程学院， 西安 710065)

射孔技术的好坏是决定油气井产能的关键要素。在恰当的射孔参数下，根据地层和施工工艺工况优选合理的射孔参数，可大幅度地减轻钻井对地层的伤害，使射孔井的产能等同于或优于理想无污染裸眼井的产能。反之，若射孔工艺不合理，射孔对地层带来的伤害可能大于钻井带来的伤害，造成油气井产能较低。由于射孔工艺在增产方面的巨大作用，国内外对射孔工艺都十分重视。甚至美国的一些专家学者认为，单单依靠改进射孔的工艺技术，就可以使油田的产能提高一倍。

Furui等[1]研究了水平井的二维表皮与三维表皮。射孔过程中主要损害原因的探明是基于Yildiz等[2]研究指出的射孔孔道顶端是主要的损害集中地，造成这种现象的主要原因是通道顶端的流型是径向流动以及模拟线性流动。同时还使用设定变量法得出了射孔参数与地层因素的交互作用是影响射孔流的最主要因素。Li等[3]对理想流的二维解析解模型进行分析，同时结合有限元得出圆辐射、轴向流模型以及径向流模型。研究表明在射孔过程中，射孔角度也是影响射孔深度的一个重要条件，射孔角的合理选择可以更易于地层的伤害区的克服。Naoto等[4]利用有限元分析法研究了射孔交互作用对射孔稳定性的影响，研究结果提供了各种影响因素作用下，管柱内流体与管柱强度的变化规律。

相比于国外，国内曲占庆等[5]、熊军等[6]、汪志明等[7]在吸取过国内外其他学者的研究成果的基础上，研究了射孔工艺参数对产能的影响规律，针对边界压力与适用范围等诸多问题进行了修正，确定了井口产能的影响因素。李士斌等[8]、徐兵祥等[9]通过有限元模拟软件研究了在定量条件下孔深、孔密、孔径、孔眼相位对产能的影响规律，并利用正交实验法，对各影响因素的权重进行了分析。文敏等[10]、许杰等[11]、肖遥等[12]应用数值模拟及实验的方法开展了基于套管强度的射孔参数优化设计。至此国内关于射孔参数的研究有了重大的进展，甚至可以说在某些领域已经达到了国际先进水平。

现将采用当今主流的数值模拟方法对射孔优化工艺进行研究，使用ANSYS对各个要素的影响程度进行分析。显然数值模拟方式相较于以往的研究方法，具有可重复、低成本、可以了解系统内部细节等优点。面对各种复杂情况与多因素影响，数值模拟可以通过修改模型参数、增加变量等方式获得结果。故在文献[13-14]研究的基础上，提出射孔参数优化的新方法，为油气田套管射孔完井工艺优化的深入研究提供参考。

1 射孔井产能半解析模型

产能的影响因素如下：①射孔因素，例如孔深、孔径、孔密、射孔格式、压实程度和压实厚度、相位；②地质因素，例如渗透率的各向异性、油井半径以及供给半径；③工程因素，例如污染深度L、污染程度K。

1.1 产能计算公式

为了方便建立模型，考虑到地层及其内部流体的各种性质，假设如下。

(1)油层是单层、厚度恒定，形状是柱形。

(2)油层流体为单相不可压缩流。

(3)流体流动形式为层流。

(4)供给半径远大于井眼穿透半径。

(5)各向异性比在地层中恒定不变。

根据油气井径向流动公式[15]可得

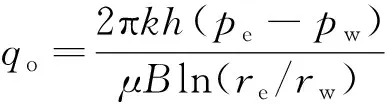
(1)

式(1)中：qo为完善井产量，t；k为地层渗透率，μm2；h为地层厚度，m；pe为边界压力， MPa；pw为流动压力， MPa;μ为地层原油黏度， MPa·s；B为原油换算系数，m3/t；re为供给边界半径，m；rw为油井半径，m。

射孔过程会对地层造成损害，其在稳态下的产能公式[15]为

(2)

式(2)中：qp为油井产量，t；Sp为射孔孔眼表皮系数；Sdp为射孔损害表皮系数。

1.2 产率比的计算

为了直观地表示射孔井的产率，可以将裸眼井与射孔井的产能之比定义为产能比，即

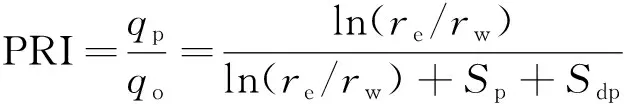
(3)

由式(3)分析可知，影响油井产能比的主要因素为射孔井所附加的表皮系数，根据对储层的损害机理不同，可将表皮系数分为射孔损害系数和射孔孔眼表皮系数。其中，射孔孔眼表皮系数包括平面流表皮系数SH、垂直流表皮系数Sv以及井筒效应表皮系数Swb。射孔井表皮系数可以看作是以上3个系数的叠加效果，具体的表达式为

Sp=SH+Sv+Swb

(4)

射孔孔眼表皮系数与射孔参数密切相关。

射孔压实损害表皮系数可表示为

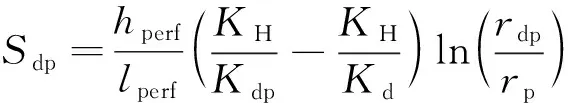
(5)

式(5)中：KH为地层水平渗透率，μm2；Kd为钻井污染区的渗透率，μm2；Kdp为压实带渗透率，μm2；rdp为压实带半径，μm；rp为射孔孔眼半径，μm。

基于上述分析，得到射孔井产率比计算公式为

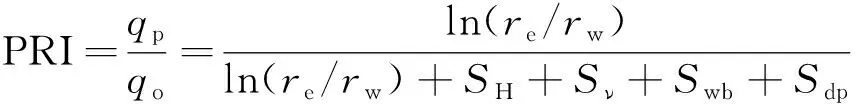
对于北方气候较为干燥的地区，灌溉工作变得更加重要。对于整地情况良好、土地平整的情况，主要采用地面灌溉方式，保证植物生长。但这种方式容易造成土壤板结，因此需要进行一定的改良。对于地势不平或者灌溉条件差的位置，为提高作业标准，加强管理，通常会选择地下灌溉、喷灌或者滴灌的方式为花卉的生长提供必要的水分。由于硬水中存在不被植物吸收的营养物质，所以园林花卉灌溉通常使用的是软水，尽量使用河水、池塘水或者湖水进行灌溉，禁止使用工业废水灌溉花卉。由于井水的温度较低，对于植物生长具有一定的不利影响，因此应尽量避免使用井水。同时在种植过程中还应根据花卉的品种以及温度、湿度、季节进行灌溉调整，通常中午不宜浇水。

(6)

基于油气井的产能比公式[式(6)]可对各种不同射孔参数组合的产能比进行计算。因此，可在此基础上进行射孔参数的优化设计及敏感性分析。

2 射孔井产能数值模拟仿真研究

2.1 射孔完井方案设计

考虑孔深、孔密、孔径与相位对产能的影响，应用二次正交实验进行分析研究，将4个因素依次编号为A(孔深)、B(孔径)、C(孔密)、D(相位)。每个因素取4个值，以保证实验具有较好的代表性与可靠性，通过二次正交设计得到16种射孔完井实验方案，如表1所示。

表1 射孔实验方案

2.2 射孔井产能几何模型

采用ANSYS中集成的SPACECLIAM进行实体建模，建模过程中规定如下。

(1)把泄油体视作柱形，其尺寸不做要求，水平井的位置取位于泄油体的中央，贯穿油层。

(2)假设在相同射孔弹的情况下，所射出的孔眼全部为形状规则直径相同的圆柱体。

(3)将井筒和井眼都视为规则圆柱体，且将井筒和井眼视为渗透率无限大的实体。

选用ANSYS集成的网格划分软件meshing对所建的几何模型进行网格划分，对于井筒和射孔孔眼区域，采用较细的网格划分方式，而对于外圈地层，采用较大的网格，以减少网格的整体数量。所建模型如图1所示。

2.3 边界条件

采用κ-epsilon流体流动模型，几何模型参数及边界条件如表2所示。

2.4 基于正交实验的数值模拟结果分析

图1 射孔井产能几何模型Fig.1 Geometric model of perforated well productivity

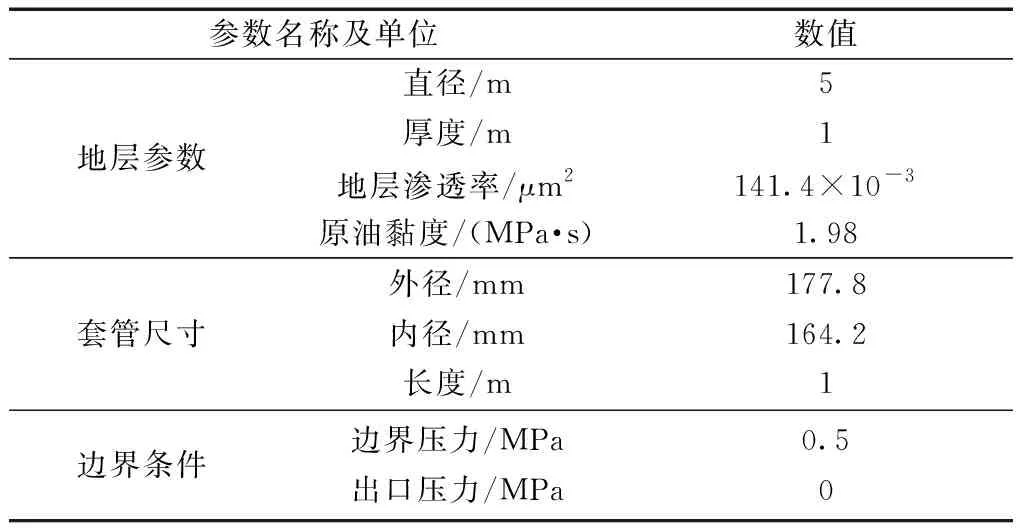
表2 几何模型参数及边界条件

表3 正交实验结果

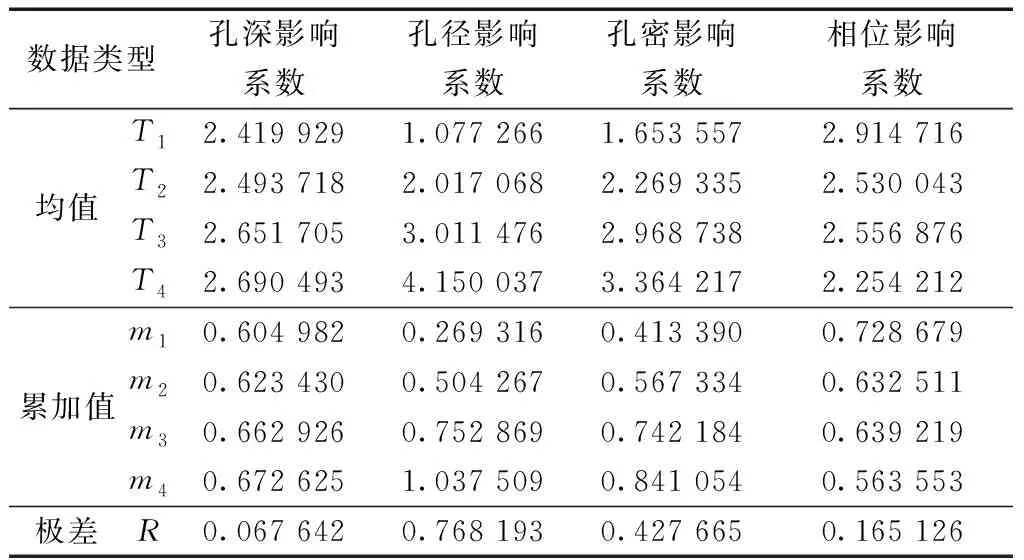
表4 正交实验结果分析

由模拟结果可知，8号实验的产率比最高，达到了1.154 714，相应的组合为(A=500 mm，B=12 mm，C=24 孔/m，D=90°)是当前最好的组合搭配。下面通过直观分析法分析各个因素的主次关系。

计算各因素在每个实验方案下的平均转化率，如表3所示，T1、T2、T3和T4的孔深影响系数表示孔深为400、500、600、700 mm时，4次正交实验的产率比之和；同理，T1、T2、T3和T4的孔径影响系数表示孔径为6、8、10、12 mm时，4次正交实验的产率比之和；T1、T2、T3和T4的孔密影响系数表示孔径为12、18、24、30 孔/m时，4次正交实验的产率比之和；T1、T2、T3和T4的相位影响系数表示孔径为60°、90°、120°、180°时，4次正交实验的产率比之和。m1、m2、m3和m4对应的影响系数为T1、T2、T3和T4对应的孔深影响系数、孔径影响系数、孔密影响系数和相位影响系数的平均值。由m1、m2、m3和m4的值，还可以得到4个平均值的极差，如孔深的极差值R=max{m1，m2，m3，m4}-min{m1，m2，m3，m4}=0.067 642。

由上述结果分析可知，当孔深增大时，产率比增大，如图2所示，在孔深较小时斜率会变大，穿孔深度达到了钻井污染带深度时，拐点出现，斜率变小。即穿孔深度对产能的作用在射孔没有穿透污染带时比较明显，在射孔穿透污染带以后明显减小。

随着孔径的增大，产率比增大，如图3所示，在实际射孔过程中，考虑到套管强度的问题，孔径应在保证套管强度的情况下尽可能取最大值。

孔密增大时，产率比增大，并且当孔密增大时，其产率比上升趋势减弱，如图4所示，同时孔密不能无限制地增加，应当考虑射孔器能力、射孔成本及套管强度等因素。

随着相位角的增大，产率比减小，如图5所示，

图2 孔深对油井产率比的影响Fig.2 Influence of hole depth on oil well productivity ratio

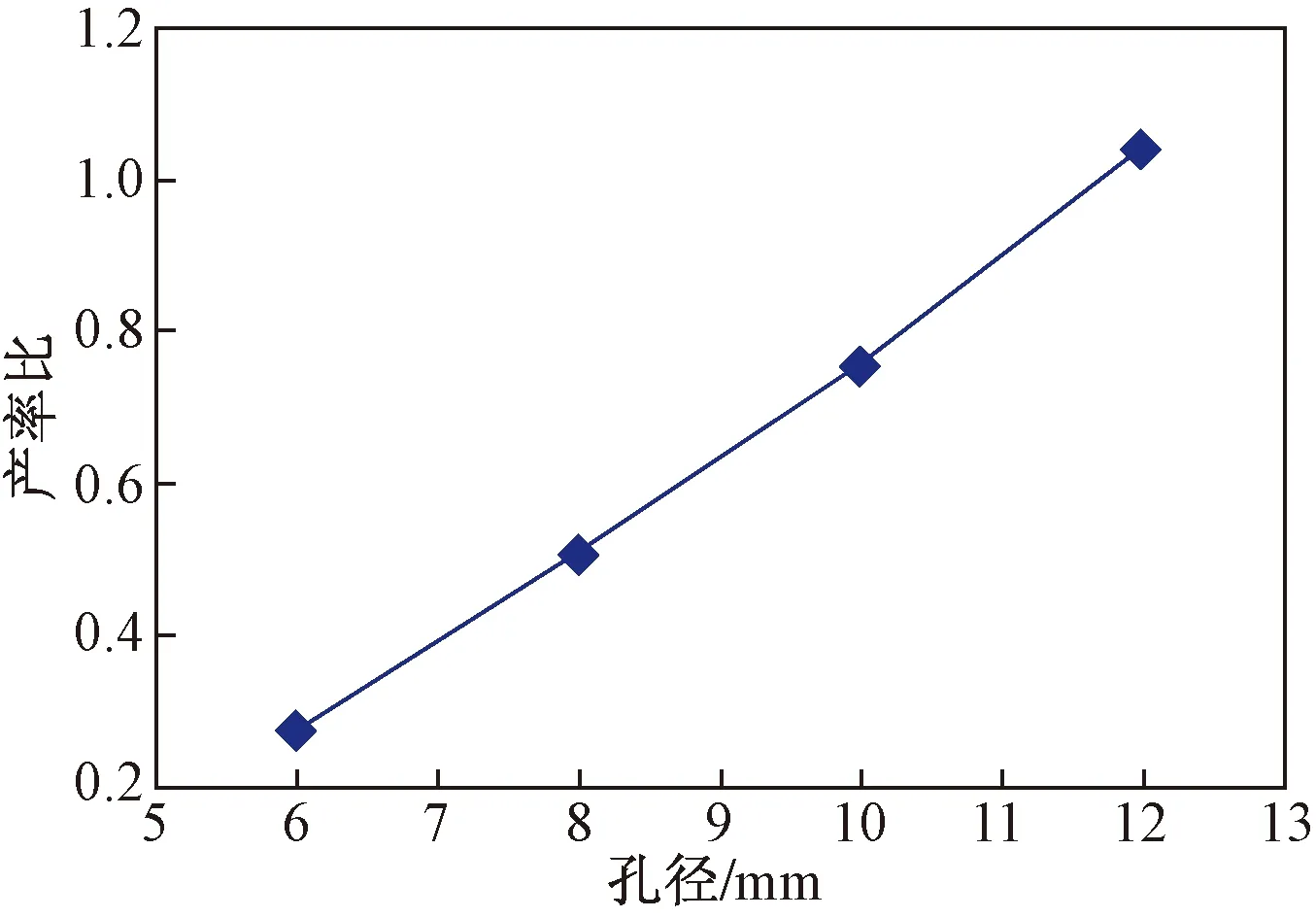
图3 孔径对油井产率比的影响Fig.3 Influence of pore diameter on oil well productivity ratio

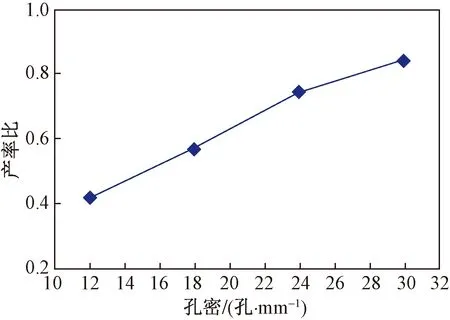
图4 孔密对油井产率比的影响Fig.4 Influence of hole density on oil well productivity ratio

图5 相位角对油井产率比的影响Fig.5 Influence of phase angle on oil well productivity ratio

相位角在60°～90°改变时，产能提高显著。

在一项实验中，各因素对实验响应的影响是有先后次序的，在该实验中，当一个因素为主要因素时，这个因素不同值之间的产率比的差距较大，当一个因素为次要因素时，其相应产率比之间的差距就较小，通过比较极差值R来判断各个因素的主次关系，可得在实验条件下，对产率比的影响重要程度排序如下：B(孔径)>C(孔密)>D(相位)>A(孔深)。

2.5 射孔参数敏感性分析

2.5.1 孔深与孔密对油井产能的影响

由于射孔完井影响因素的复杂性，通过数值模拟方法，对各影响因素进行综合分析，设定相位角为90°，孔径为6 mm时，分析孔深与孔密对油井产能的影响规律，如图6所示。

图6 孔深与孔密对产率比的影响Fig.6 Influence of pore depth and pore density on productivity ratio

由图6可知，当射孔密度不同时，射孔井的产率比改变较为显著。在相同的射孔深度下，射孔密度越高，油井的产能比值就越高。例如在相同的 400 mm 射孔深度时，在射孔密度为12 孔/m时，油井的产率比为0.31。而当射孔的密度提升至18 孔/m时，油井的产率比为0.38。相比与12 孔/m时油井产能比有了大幅提升。因此，在实际射孔完井过程中，如遇到设备限制或者地质情况较差，使得射孔的深度难以达到要求时，可以通过增加射孔密度来达到提升产能比的目的。同时由于在射孔过程中受制于射孔设备与套管强度的影响，射孔密度不可能是无限大的，因此不能通过无限制地增加射孔密度来提高产能。

2.5.2 孔深与相位角对油井产能的影响

设定孔密为12 孔/m，孔径为6 mm时，分析孔深与相位角对油井产能的影响规律，如图7所示。由图7可知，在相同条件下，相位角为60°时产率比最佳，180°相位角时射孔效率最低。并且随着孔深的增加，4条曲线的产能比增长趋势都有下降的趋势，说明射孔深度在达到一定值时，对油井产能的贡献开始减弱。90°相位与120°相位的曲线仅近似为平行关系。在研究的条件下，选择60°相位角作为射孔相位。

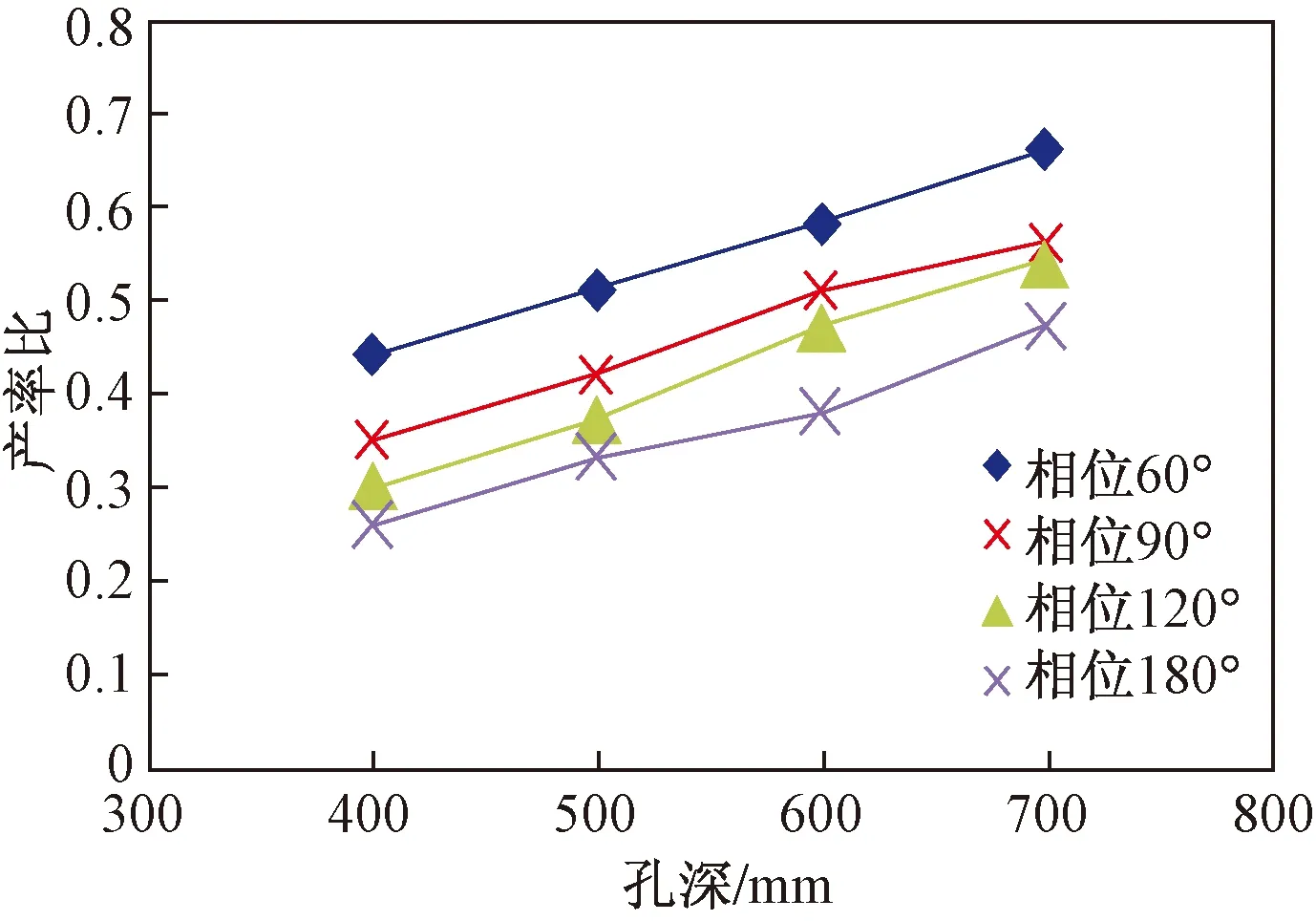
图7 孔深与相位对产率比的影响Fig.7 Influence of pore depth and phase on productivity ratio

2.5.3 孔深与孔径对油井产能的影响

设定孔密为18 孔/m，相位为180°时，分析孔深与孔径对油井产能的影响规律，如图8所示。由图8 可知，当孔深与孔径增大时，油井产率比增大；孔深较浅时，油井产率比受孔径的影响较大，当孔深达到一定深度时，油井的产率比受孔径的影响减小，同时增大孔径对套管的强度也会产生一定的影响，因此，在射孔过程中，需要选择合适的孔径进行射孔。

图8 孔深与孔径对产率比的影响Fig.8 Influence of pore depth and pore diameter on productivity ratio

3 结论

(1)基于解析方法，建立了考虑射孔参数的产能计算公式，并得到射孔井与裸眼井产率比计算公式，为射孔井产能预测提供理论模型。

(2)借助有限元方法建立了井筒渗流模型。在考虑孔眼、孔径、孔密、相位的情况下，采用正交实验法建立了系统数值模型，确定了不同射孔参数下的产能比。

(3)利用直观分析法与敏感性分析法，对有限元数值模拟所得到的数据进行分析，得到了各个影响因素之间的主次关系与各个因素随数值的增长对产能比影响趋势的变化，为实际的油田射孔操作提供了可供参考的依据。

(4)由分析结果可知，各个因素对产能比的影响比重依次为孔径、孔密、相位、孔深。孔径对射孔井产能比的影响最大，孔密与孔径一样数值越高产能比越高，孔深在深度较浅时对产能比影响较为明显，随着深度增加其效果逐渐减弱。