基于卡尔曼滤波的无源定位精度分析

李永生，董光焰，陈 凯，谢亚峰，唐金力

(1 中国电子科技集团公司第二十七研究所，郑州 450047；2 河南省激光雷达与大功率应用技术重点实验室，郑州 450047)

0 引言

随着电子信息技术的飞速发展，电子侦查是现代电子作战体系中十分重要的一环，目标定位跟踪技术是电子侦查技术重要问题之一。在军用领域，目标定位跟踪技术广泛用于光电吊舱、无人机、巡飞弹等对目标进行位置侦查、作战效果评估等。在民用领域，目标定位跟踪技术还广泛用于地图绘制、地质灾害预测等领域。常用的目标定位跟踪方法可分为有源定位和无源定位，有源定位基于方位角测量和距离测量，通过主动发射电磁或光电信号测距，跟踪目标获得相对角度关系，计算目标位置。无源定位系统在自身不发射任何信号的情况下，完全依靠被动接收辐射源目标的电磁和光电信号，确定目标的位置和运动状态，具有隐蔽性强、抗干扰能力强、作用距离远等特点。

无源定位系统不直接测距完成目标位置信息解算，定位的实现方法通过自身平台的快速运动获得辐射源的角度或频率信息，经过多次测量不断消除剩余误差最终获得目标精确位置信息。1997年Lockheed Martin公司和艾那伦微波公司研制出了一种基于数字射频存储器的无源测距系统，圆概率误差优于1%。后续开展的测向和定位系统(DFLS)、精确定位与识别系统(PLAID)、联合研究开发项目(CRADA)等均基于无源定位原理实现了对目标的精确定位。国内在无源定位技术方面研究起步较晚，孙仲康等最早开始对单站无源定位技术进行针对性研究，后续国内高校相继开展了无源定位技术方面的研究工作。

以某侦测平台的红外导引头为研究背景，将侦测平台与红外导引头的信息进行综合处理，通过对目标方位角的多次观测，建立目标无源定位的系统状态方程和观测方程，利用扩展卡尔曼滤波(extended Kalman filter，EKF)算法计算目标位置，研究不同侦测平台速度、飞行轨迹、平台自身定位精度等对计算结果的影响，有针对性的确定滤波参数，适合在小型无人机、巡飞弹、精确制导导弹等平台上应用。与传统有源定位方法相比，无需发射主动信号测距，具有隐蔽性强、适用范围广、结构简单等突出优点，具有较大的军事应用前景。

1 目标定位原理

1.1 几何原理

理论上如图1所示，利用导引头测量两个不同位置的方位角信息及位置信息可确定两条直线，若观测目标静止，则两条直线交点即观测目标的位置。利用搭载导引头的侦测平台提供的位置、速度及姿态信息，可确定两个观测时刻的直线位置及方向，利用几何原理可定位待侦查目标的空间位置。

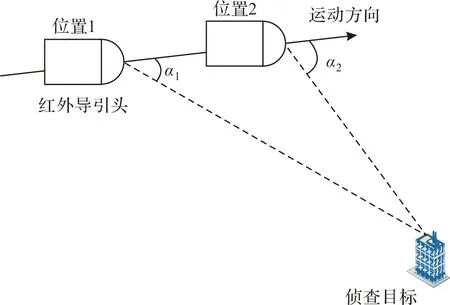
图1 无源定位系统几何原理(静止目标)

对于运动目标的无源定位如图2所示，不同时刻的定位线交叉后定位点会偏离目标真实位置，计算得到的目标运动轨迹也不是真实的目标运动轨迹。此时，根据几何原理，距离目标越远、侦测平台相对目标运动速度越快所计算的目标运动轨迹越准确，这就需要利用侦测平台的快速机动性，连续快速测量，增加对目标的测试频率，形成目标运动状态的估计。

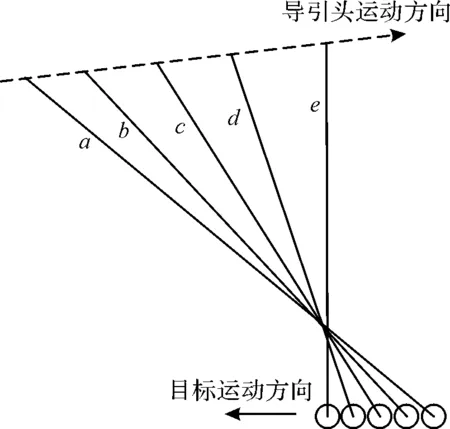
图2 无源定位系统几何原理(运动目标)

1.2 数学模型

1)系统状态方程

无源定位系统依据侦测平台的位置和姿态信息计算目标的位置信息，可以以二维平面为例，计算无源定位的数学模型。设观测目标相对侦测平台的位置为、，速度为、，加速度为、，Δ为系统数据传输周期，则系统的微分方程和离散状态方程分别为：

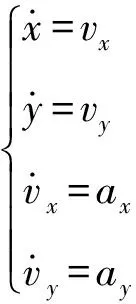
(1)

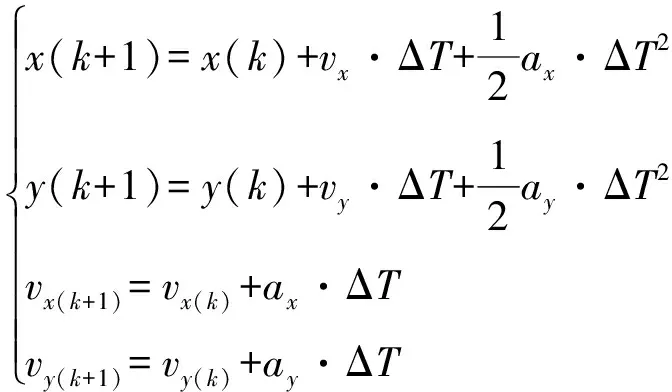
(2)

式(2)以矩阵形式可表示为：

(+1)=()()+()()+()

(3)

式中：()为位置和速度组成的观测矩阵,()=[,,,]；()为加速度矩阵,()=[,]，()为状态误差；()，()分别为状态转移矩阵和控制矩阵：

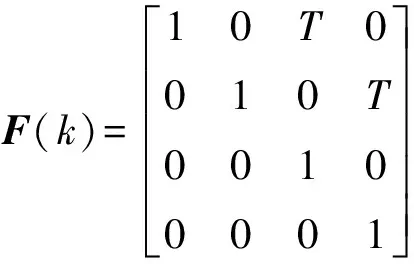
(4)

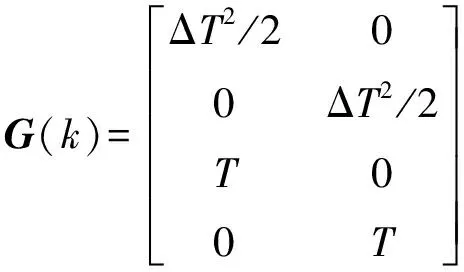
(5)

2)系统测量方程

红外导引头作为单站无源定位观测平台的单站定位系统，采用方位角作为观测量，则观测方程可表示为：

()=((),())+()

(6)

其中：()为观测量矩阵；((),() )为非线性观测函数；()为观测噪声。

2 基于EKF的目标定位算法

扩展卡尔曼滤波是在卡尔曼提出的解决非线性问题的思想基础上发展而来，该方法的基本原理是由泰勒级数展开项的前几级部分来局部线性化，同时结合经典卡尔曼滤波算法完成计算仿真。

EKF算法的递推过程如图1所示。

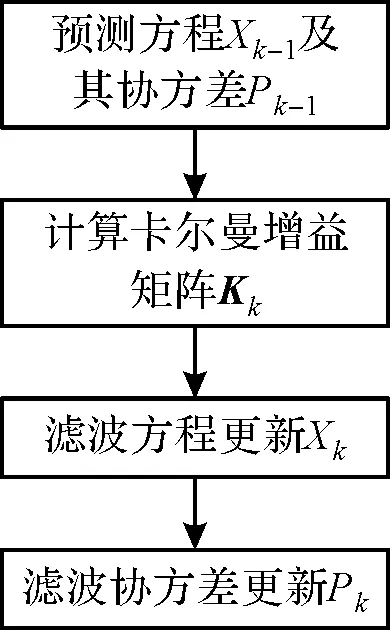
图3 EKF算法递推过程

3 误差影响因素分析

3.1 仿真条件

为了计算不同仿真条件对定位误差的影响，设计一匀速飞行的侦测平台及固定的待测目标，起始位置[50 m,10 m]，速度[200 m/s,0 m/s]，定位精度10 m，目标位置[2 120 m,1 137 m]，目标静止，观测周期=0.05 s，观测次数100次。预测目标位置[,]=[1 200 m,1 800 m]，状态预测协方差[0,0]=diag[5,4]，观测噪声2×10rad。

3.2 数据分析

3.2.1 收敛时间

图4～图6分别是仿真剩余误差曲线图、目标方向位置估算结果和目标方向位置估算结果随时间变化曲线。

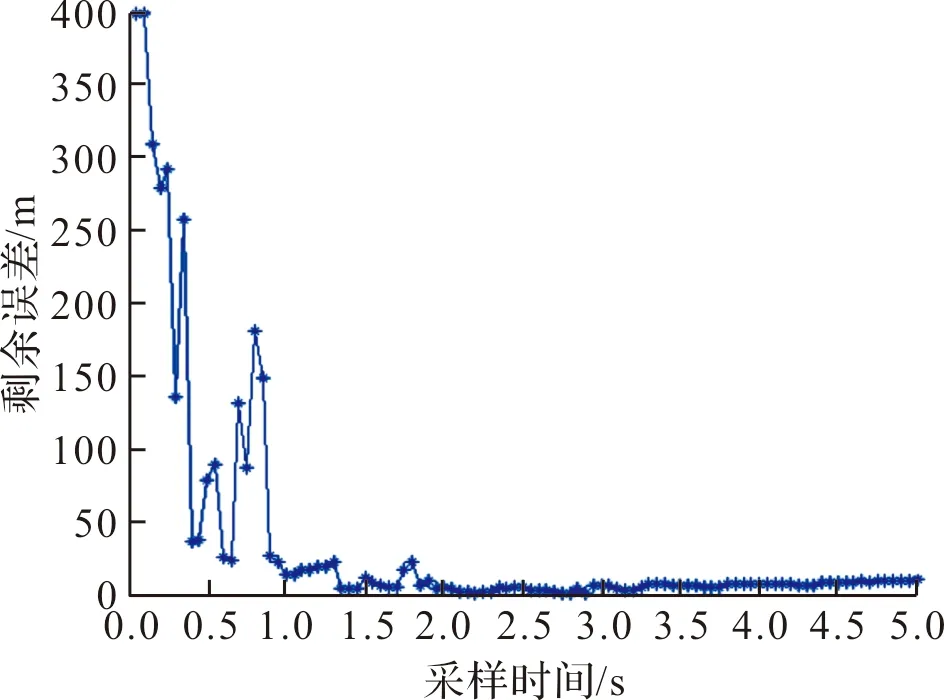
图4 剩余误差曲线

图5 目标x方向计算结果

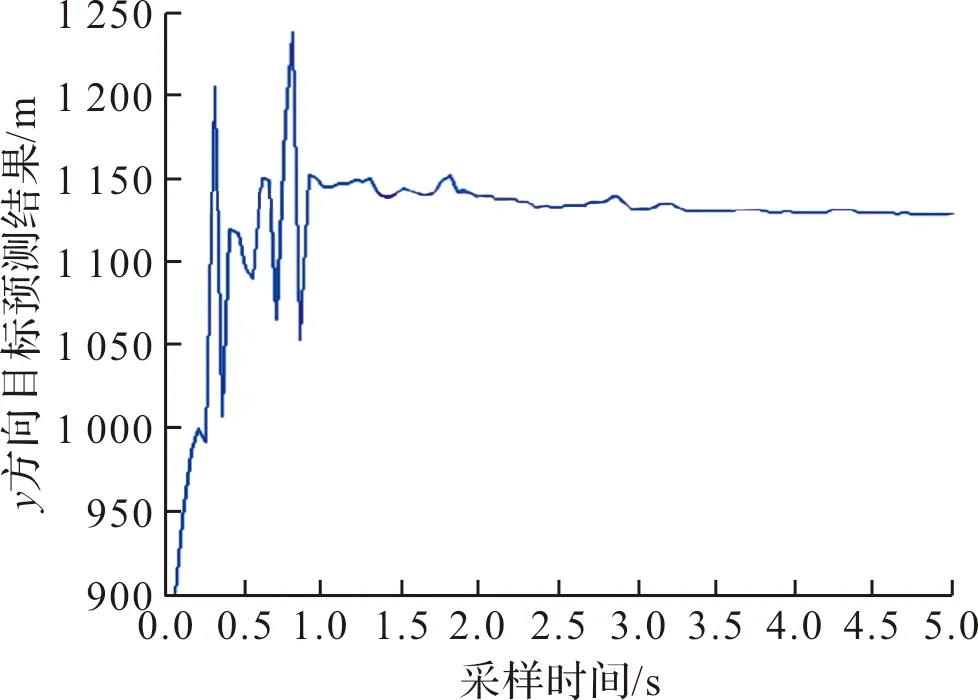
图6 目标y方向计算结果

对于静止目标的无源定位，侦查平台产生机动即可完成目标位置预估，EKF算法能够较好的进行目标位置计算，开始测量约1 s，经过20次采样和滤波计算，位置估算误差小于40 m。但是经过多次Monte-Carlo仿真发现，EKF算法对滤波参数依赖性较强，目标预估及参数选取不合理易导致仿真发散，仿真时需选取合理的滤波参数和预估范围。

3.2.2 侦测平台定位精度的影响

其他仿真条件不变，改变侦测平台定位精度分别为20 m、10 m、5 m、2 m，EKF仿真计算的目标位置剩余误差如图7、图8所示。由图中不同侦测平台定位精度条件下的剩余误差收敛情况可以分析得出，侦测平台定位精度越高，EKF算法收敛速度越快，剩余误差越小。

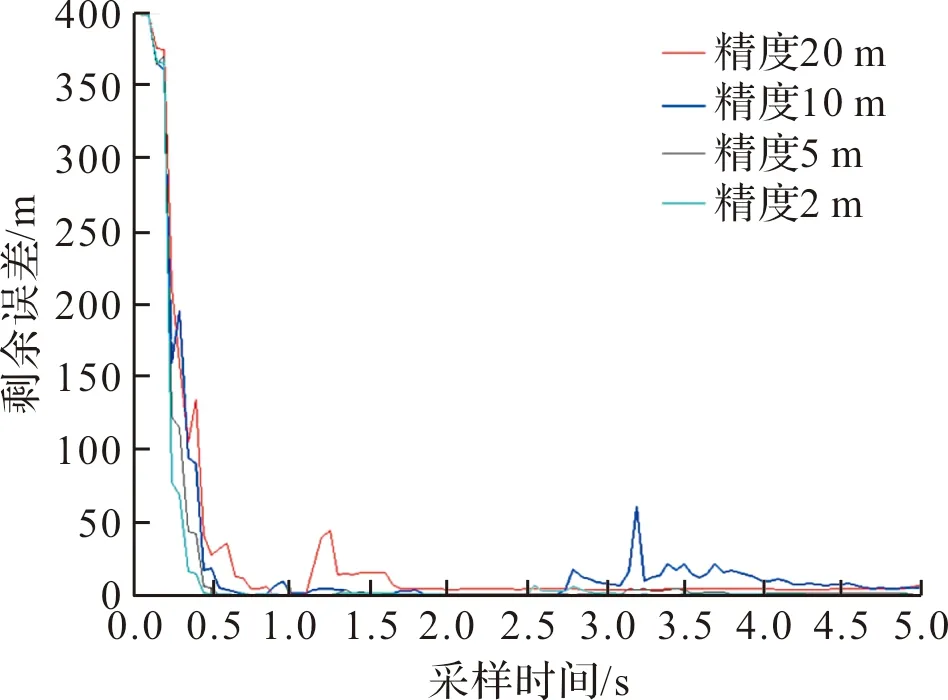
图7 不同定位精度剩余误差

图8 不同定位精度剩余误差大小

3.2.3 侦测平台飞行速度

其它仿真条件不变，改变侦测平台飞行速度分别为100 m/s、80 m/s、60 m/s，EKF仿真计算的目标位置剩余误差如图9所示。不同侦测平台飞行速度条件下的剩余误差收敛情况分析得出，侦测平台飞行速度越快，EKF算法收敛速度越快，剩余误差越小。

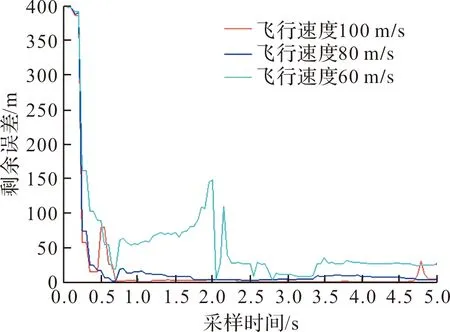
图9 不同飞行速度剩余误差仿真结果

3.2.4 导引头测角精度

分析图10不同测角精度条件下的剩余误差收敛时间，导引头的测角精度直接影响无源定位系统仿真的目标剩余误差，测角精度越精确，目标位置剩余误差越小，不同导引头测角精度的剩余误差收敛速度相当。

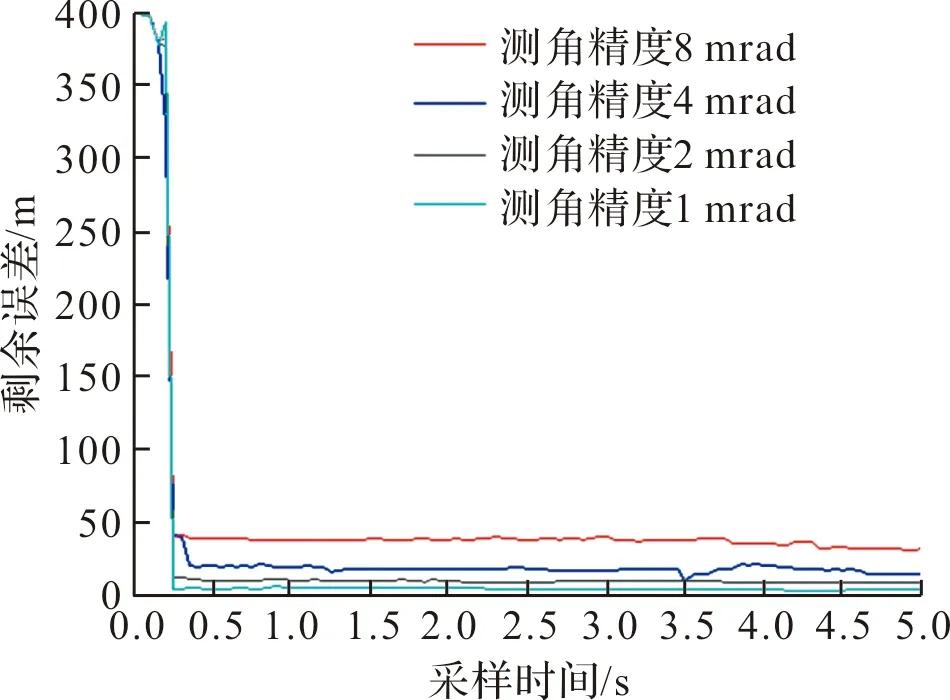
图10 不同测角精度的剩余误差

3.2.5 侦测平台与目标距离

其它仿真条件不变，改变侦测平台与目标之间的距离为2 300 m、2 000 m、1 700 m、1 400 m，EKF仿真计算的目标位置剩余误差如图11所示，随着侦测平台与目标位置的距离减小，目标位置剩余误差逐渐降低；不同观测距离的目标位置剩余误差收敛速度相当。

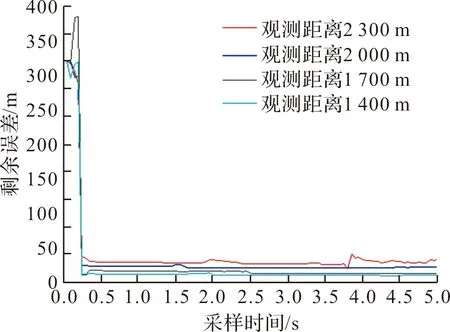
图11 不同观测距离的剩余误差

4 结论

在分析无源定位几何原理的基础上，建立无源定位系统模型和观测模型，以某侦测平台及红外导引头参数为基础进行仿真计算，验证了EKF算法性能稳定性，分析了剩余误差的收敛时间，侦测平台定位精度、飞行速度、测角精度、目标距离等对目标位置预估剩余误差的影响。形成结论如下：

1)基于EKF的无源目标估计算法收敛速度快、精度高，但算法系统参数对仿真性能有较强影响，不合理的参数设置易导致发散。

2)侦测平台自身定位精度越差，目标位置定位误差越大。

3)侦测平台飞行速度越快，目标的位置预估越准确。

4)导引头测角精度越精确，目标位置预估越精确，定位误差越小。

5)侦测平台与目标位置的距离影响定位误差，随着距离变小，定位误差变小。