基于车用柴油机不平衡数据集的故障识别组合模型

李秀峰，王宁，刘璇琦，段艳

（同济大学汽车学院，上海 201804）

发动机的工作状况直接决定汽车运行状态，因此，发动机零部件的日常维护与故障排查是十分重要的工作。发动机故障具有多样性、频发性、不确定性和破坏性等特点，使得与发动机相关的故障识别任务具有一定的挑战性。

目前解决汽车故障识别问题的主要方法是传统的专家系统。专家系统通过学习人类专家的行业经验，模拟专家发现、识别判断、处理和解决问题的能力，以达到或超过人类专家解决同等问题的能力。这种系统虽然交互性强、容易修改，但是开发周期长、对于专家能力要求高，而且相关产品难以跟上软件化、云端化的发展趋势。

在解决数据集不平衡问题时，部分专家学者使用模糊系统结合神经网络算法的方法：国外的SRILATHA D等实现了一种将模糊内核c-均值聚类算法和二型最优模糊神经网络结合而成的监测系统；Naderkhani等则基于自适应神经模糊推理系统，对于非模糊输入和对称梯形模糊输入的模糊回归函数进行了分析与预测，分析比较了非参数模糊回归统计方法中包括局部线性平滑（L-L-S）、K-近邻平滑（K-NN）和梯形模糊数据核平滑（K-S）在内的3种方法，以获得最佳平滑参数；吕晓丹等在标准模糊神经网络控制器基础上，提出了改进型模型，在模糊规则参数化及激活函数构建方面做出了改进创新，利用权重算法让模糊规则可以跟随误差率变化而调整，避免梯度消失和梯度爆炸的问题。上述基于模糊理论的学习方式在数据不完整或数据量偏少时具有一定的优越性。

针对目前在汽车领域实现发动机故障自动识别的相关研究较少，并且考虑到一般的机器学习模型受限于数据集不平衡问题，模型可识别的故障类型偏少，本文从数据层面出发，结合机器学习等研究方向已有的成熟算法，设计出一套适用于大数据样本集和小数据样本集的故障诊断组合模型：针对数据样本量较大的故障类型，采用机器学习中的XGBoost算法建立梯度提升故障识别模型；针对数据样本量较小的故障类型，采用模糊神经网络构建故障识别模型，最终获得针对汽车发动机的多适应故障识别组合模型。

图1 研究内容框架

1 数据预处理

数据源自与博世（BOSCH）公司合作研究项目。项目所提供数据涵盖4组柴油车队（编号分别为CAM09-12）的两类数据，一类数据为记录全部实时采集数据的RE（RealTime）表，另一类为记录全部故障相关数据的FT（Fault）表。RE表以秒级实时采集了车用柴油机的大量特征信息，共有63个监测参数，例如采样时间（TM）、ECU里程、Engine Speed等实时运行数据；FT表是故障信息的记录表，记录了柴油车发生故障的起止时刻、故障类型等17个监测参数。

首先对两类数据表进行有用参数的筛选。结合相关工程师经验，剔除RE表和FT表中的部分无用参数，并将SPN与FMI两个参数合并为SPN|FMI一个参数，用于结合故障手册文件进行对故障的唯一性定位。

其次，对两类数据表进行时序链接处理。TM（Time）参数为系统时间参数，精确到秒级，依据TM特征参数将两表链接得到RE-FT表文件。在双表匹配过程中，如果RE表数据链接到FT表时产生NaN格式数据填充，即意味着此时系统运行正常，无故障码数据。

最后，对于上述步骤生成的RE-FT联合表文件进行数据清洗以及去重等操作，生成2020年12个月的RE-FT联合表文件，共计1 076个，其中共含故障数据14 497条，清洗后的数据包括51个特征，去掉时间特征（TM）与故障定位特征（SPN|FMI）参数后，剩余49个有效运行数据特征。RE-FT联合数据特征参数见表1。

初中生处于青春期，心理上处于不稳定状态，生活在社会这种大环境中，经常受生理上、心理上、情感上的困扰。这些问题若不及时正确引导和处理，很容易导致学生的心理失去平衡。课堂教学中应积极渗透学生的心理健康教育。

表1 RE-FT联合数据特征参数

机器学习模型的训练需要足够的样本，并且要保证各类样本具有代表性并均衡分布，才能使模型效果既不欠拟合也不过拟合，具有较好的泛化能力。为确定是否需要进行数据平衡，对故障数据中所有故障类型进行计数，再对各类数据进行按量级分桶统计，选取0，10，20，40，50，100，200，400，800，20 000作为样本分层分割点，并计算该条件类别故障数占总故障数百分比，数据分类统计结果见表2。

表2 故障数据分类统计

2 基于大数据的XGBoost识别模型

2.1 XGBoost算法原理

采用决策树作为弱分类器的梯度提升算法被称为GBDT（Gradient Boosting Decision Tree）算 法，GBDT中使用的决策树通常为CART分类及回归树。但GBDT与传统的Boosting有很大的不同，传统的Boosting侧重于正确和错误的样本加权，GBDT的每次计算都是为了减少前一次的残留误差，进而可以在残差减少的梯度方向上建立新的模型。

XGBoost是基于GBDT改进而来的，主要增加了正则项和采样来防止过拟合，并且利用对于代价函数的二阶泰勒展开，使得算法可以同时使用一阶和二阶导数，二阶导数有利于梯度下降得更快速和准确，而由于泰勒展开函数的特性，可取展开函数做自变量的二阶导数形式，在不选定损失函数具体形式的情况下，单纯依靠数据输入就可以进行叶子节点分裂优化计算。XGBoost的核心算法可以总结为不断特征分裂，每次向计算系统里添加一棵树，学习一个新的函数，来拟合上次预测得到的残差，训练完成时，样本特征在经过分类决策之后分布在每个叶子节点上，因而每个叶子节点对应一个分数，最后将每棵树对应分数相加即为该样本预测值。XGBoost算法中，叶子的分裂方式，即节点的分裂方式基于贪心算法发展而成，贪心算法主要是利用枚举法将所有树的结构遍历，利用打分函数来选取最优结构的树，将此结构的树加入模型中，不断重复和迭代，直到触及阈值节点数或设置的超参数max_depth则停止建立决策树，避免树生长太深导致学习局部样本，最后得到过拟合结果，使泛化能力下降。

2.2 平衡数据

平衡数据包括重新采样、集群丰富度、交叉验证等方法。

2.2.1 重新采样

重新采样包括欠采样和过采样两种处理方式，这里由于稀有样本过少，即使采用自重、合成、复制等方法也仅仅是放大现有特征，可能导致最后偶发特征固化，使机器学习将无关参数判定为有效特征的情况，因而选用欠采样，减少丰富类数据数量，即限定单种故障最多投入数据量，在重新采样阶段就以50的10倍作为数据上限，限定单个故障类型最多投入500条故障数据进入训练，另外加入正常数据5 000条。

2.2.2 集群丰富度

集群丰富度是通过对丰富类数据进行聚类操作，选取集群分布的集群中心与稀有类数据进行训练的方法。本文选用-means的集群方式，取值为120，即取稀有类数据中每一类样本个数为120，并将这个数值作为选取聚类中心点附近数据的个数，这样就可以在保持特征不变的情况下得到均衡样本。进行聚类取中心点操作后，接下来就可以将相等样本量的各类故障数据投入模型中进行监督训练。

2.2.3 交叉验证

-fold交叉验证也是平衡数据的一种方式，这种方式的原理是把原始数据随机分成份，然后每次进行训练时，随机选取一个部分作为测试集，剩下-1个部分作为训练集，然后在保证每次选取的部分互不相同的情况下将验证进行次，最后将得到的结果取均值，即可得到更加均衡的数据集输入。

2.3 模型识别效果

将数据集按照9∶1的比例分割为训练集与测试集两部分，为得到准确的评估结果，本文采用分层抽样的方式划分数据以保证测试集和训练集中各类样本的分布情况大致相同。在XGBoost识别模型中所涉及的调节参数及实际取值见表3。

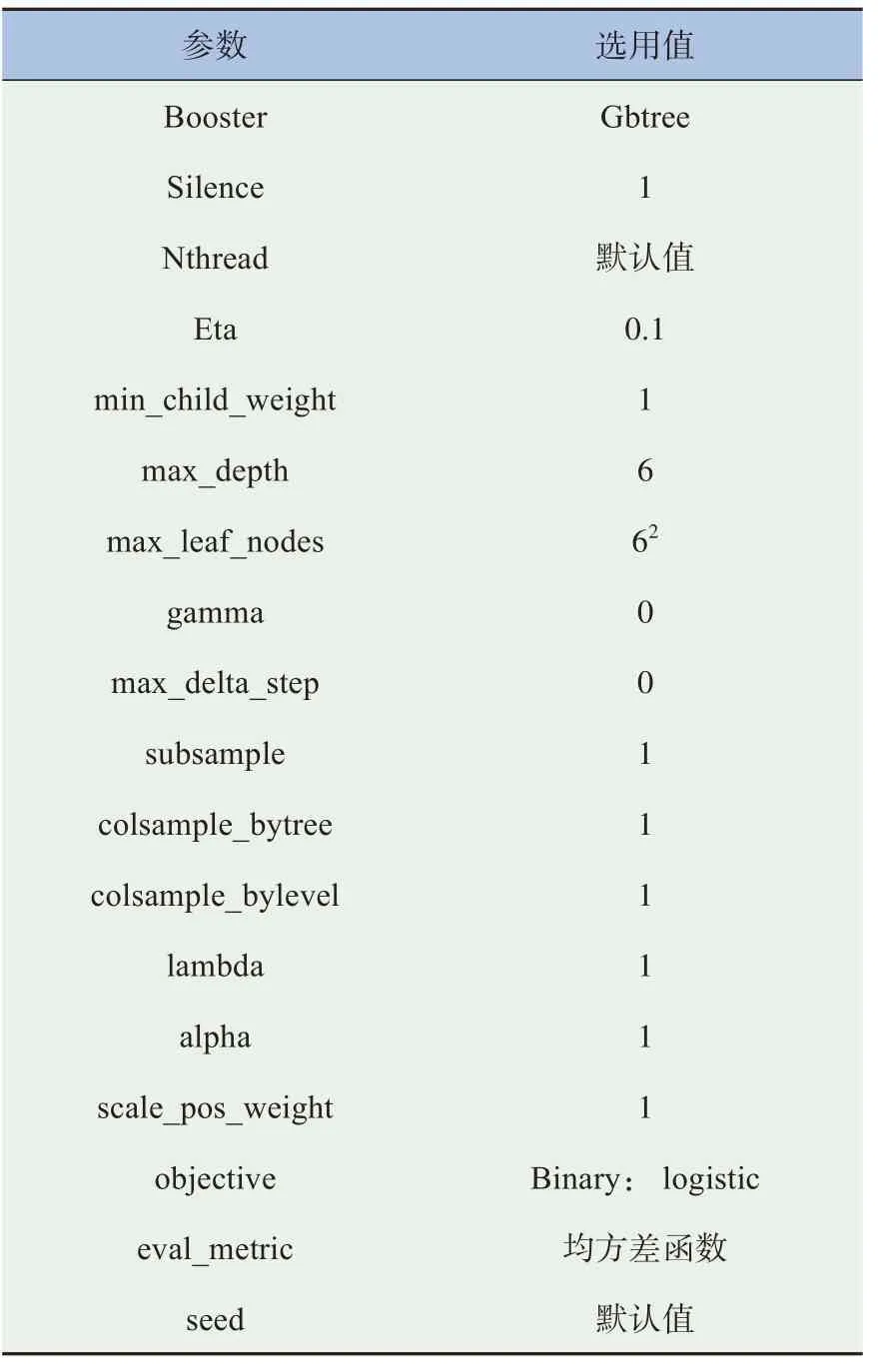
表3 模型参数取值

利用不同的数据平衡方式配合参数微调，采用宏平均（Macro Average）和权重平均（Weighted Average）两种方式对所有故障取均值作为总评估值，这两种评估计算方式的主要差别在于计算Macro Average时对于每一样本类赋予相同权重，但是当样本量不够均衡时，按照数据体量赋予每一类不同权重的Weighted Average更加准确。利用两种计算方式在查准率（precision）基础上进行模型识别泛化能力评估见表4所示，进行识别准确度范围约为86%～92%。

表4 XGBoost模型识别效果 单位：%

3 基于小量数据的模糊识别模型

3.1 模糊系统与神经网络概述

在XGBoost模型中被弃用的故障类型数据，本文利用模糊系统结合神经网络算法进行处理，这种基于模糊理论的学习方式在数据不完整或数据量偏少时具有一定的优越性。

模糊系统是一种基于知识或基于规则的系统，它的核心就是由IF-THEN规则表达的知识库，是一种将多输入非线性映射为单输出的运算系统，如果想进行多输出映射，可将单输出叠加称为多输出得到。一个模糊系统的模糊规则库里可能有许多规则，而模糊推理机就是为了高效进行模糊推理而产生，它的作用主要是在模糊集上根据模糊规则完成一系列复杂运算和规则判定。由于模糊系统自身仅仅是执行已有规则进行判定，不具有自主学习能力，也不能自我纠错，可以认为是封闭后就不再有改变的控制系统，而且对于规则过多或规则之间彼此比较相近的模糊系统，模糊推理机在进行规则执行时有可能会有多条模糊规则响应，导致输出超载，最终无法输出或输出不准确的结果。

神经网络对来自同一分布的输入，能产生准确的输出，也就是说在训练完毕后，采用没有输入过的测试集进行测试时，神经网络应该能够对训练集内的映射进行运算，可以对测试集数据达成类似的映射效果。因而可以这样说，相比模糊控制系统，神经网络不仅仅是对于输入输出信息学习映射函数，还可以通过挖掘数据自身特质来学习并建立规则，而不是单纯执行已有规则。

3.2 构建模糊神经网络模型

模糊系统和神经网络各自有其优缺点，其中前者主要着眼于执行，缺乏自学习能力，后者学习函数关系，但其权值与学习能力关系难以总结为公式规则，不便于清晰阐述，并且模型构建速度和精度受诸多因素影响，难以处理高层次信息。因此考虑将二者结合，既能利用模糊器的优势，即把非公式化输入基于可公式化的If-Then规则输出非公式化结果，又能结合神经网络自学习能力，即挖掘数据之间关系实现对系统自身进行纠错与演化。基于模糊控制的模糊神经网络识别模型的建模流程如图2所示。

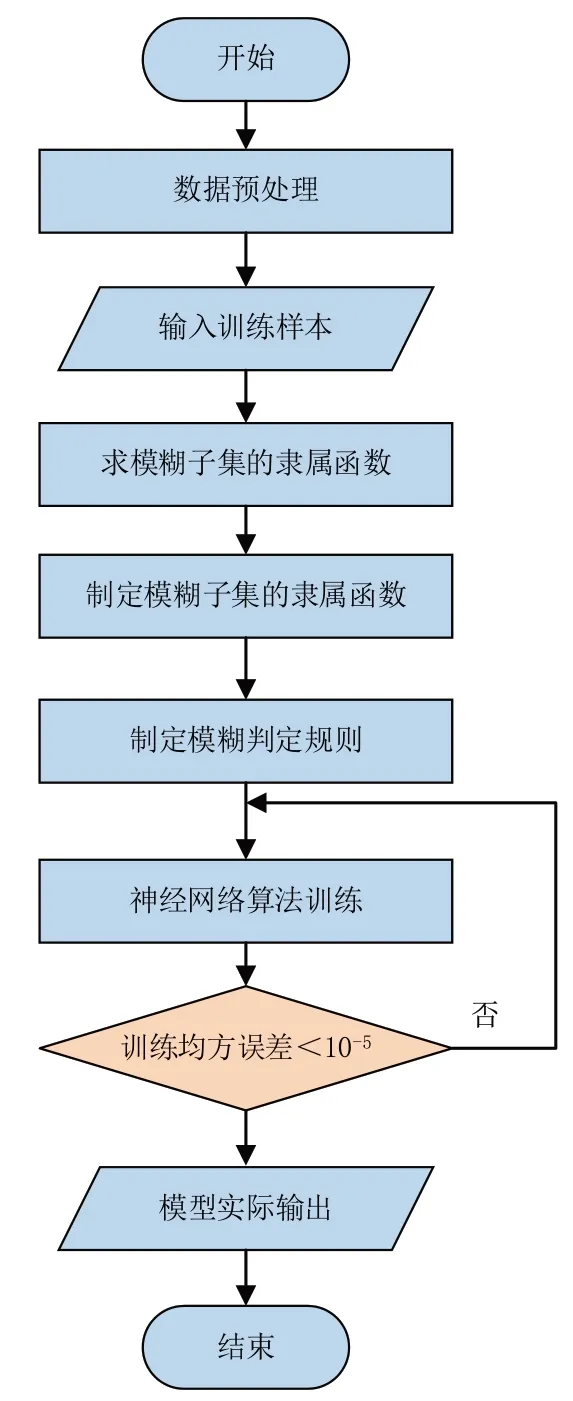
图2 模糊神经网络识别模型的建模流程

对于模糊识别输入数据，选取2020年12个月内故障发生频次大于20但不大于100的小量数据故障，根据表2可得共8种故障，本文选取30个运行数据特征作为系统输入参数，建立集，分别以，.……来表示，将8种故障类型作为系统输出参数，建立集，分别以，，…，来表示。

模糊神经网络模型主要由输入层、模糊层、隐含层和输出层构成，其中隐含层数决定了模型训练的精度和速度。基于小量数据的模糊神经网络模型的隐含层数选用10层，加上输入层、输出层及模糊层，神经网络总层数为13层，属于正常算力范围之内。

模型深度确定后，需要建立模糊推理表，为参数部分状态赋值Nomal，其余参数变化 范围则分为High和Low两类，分别用H、N、L来进行代替。此外，为使系统可以输出无故障Nomal或近似Nomal结果，对故障输出设定门槛，即为输出增加可信度判定机制，此处首先选用=0.65，表示有65%概率为当前故障，结合H、N、L参数，尝试建立模糊规则表，最后建立模糊多层感知器如图3所示。

图3 模糊多层感知机

最优的模型必须同时满足两个条件：梯度最优和损失函数最优。梯度最优是指在利用训练集进行训练时，在梯度最小前提下获得最小损失函数，此时代表模型训练最成熟；损失函数最优是指训练集损失函数曲线与测试集损失函数曲线重合度最高，这代表模型具有良好的泛化能力与鲁棒性。倘若有两个以上训练结果同时满足以上两点，观察选取梯度曲线和均方误差曲线最平滑的训练结果作为最优模型。本文选用均方误差作为损失函数，以衡量模糊神经网络模型的学习效果。

3.3 模型识别效果

结合学习模型反馈要求，选用神经网络包括BP神经网络、NN工具箱两种在Matlab中可直接调用的神经网络工具箱，并按照7∶1.5∶1.5的比例分割训练数据、验证数据、测试数据。模型训练周期为70时的整体拟合效果较好，其损失函数及梯度下降曲线如图4所示，测试集均方误差函数与训练集均方误差函数几乎重合，证明输出值与实际值非常接近，模型分类识别效果较好，梯度下降曲线十分平滑，模型成熟。

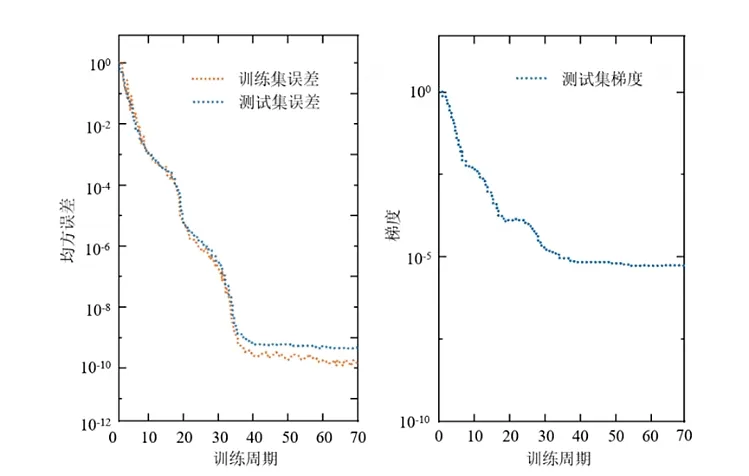
图4 均方误差与梯度随训练周期变化图

多次测试后对于投入模型的故障识别结果计数并基于准确度计算概率，选取众数识别准确度，得到识别准确率如表5所示，模型平均识别准确率为67%。

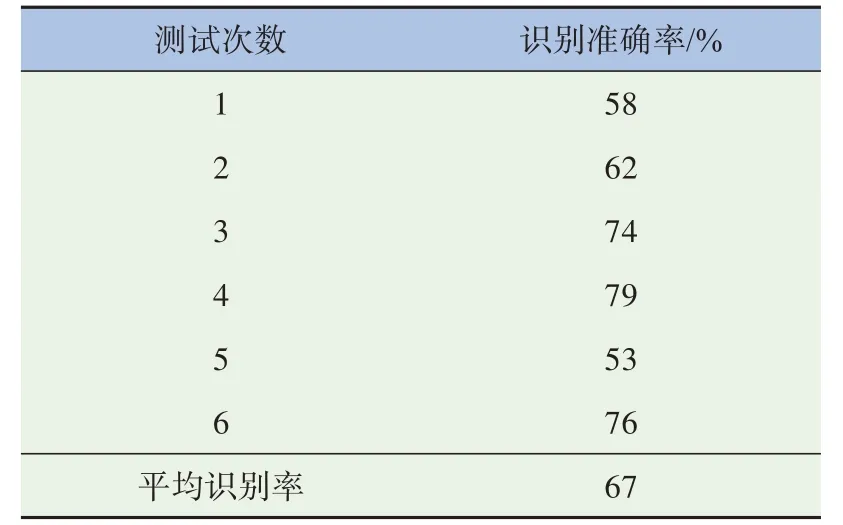
表5 模糊神经网络模型的识别准确率

4 结语

本文建立了一种能够覆盖更多故障种类的多适应发动机故障识别组合模型。模型由两部分组成：第1部分是适用于数据完备情况下的基于大数据的XGBoost分类模型，模型准确率最高达到92%，可以准确、高效地进行发动机故障检测，并且不依赖于人工，在增加故障判断准确度的同时还可以减少人工成本；第2部分是针对部分低频故障但检测优先级别高的重要故障，如进排气异常、喷油器异常等，在排除偶发性、不可预测的随机故障后，在数据不完备情况下的构建模糊神经网络识别模型，最后模型识别效果达到67%。