地震作用下黄土边坡动力响应的时频特征分析

2022-10-11张兴臣梁庆国曹小平

地震工程学报 2022年5期

张兴臣,梁庆国,2,孙文,曹小平,2

(1.兰州交通大学土木工程学院,甘肃兰州 730070;2.甘肃省道路桥梁与地下工程重点实验室,甘肃兰州 730070)

0 引言

我国黄土地区大多处于地质构造发育、地震活动频繁的区域,历史上强烈地震动作用导致的以滑坡、崩塌等为主的地震地质灾害,曾造成巨大的人员伤亡和经济损失,并对自然环境造成严重破坏。因此,研究黄土边坡在地震动力作用下的动力响应特征与破坏机制,并提出相应的防控措施成为岩土科学界的热点问题[1]。早期,国内外学者[2-4]主要从动力稳定性的角度研究边坡动力失稳,并取得大量研究成果[5-8]。

目前,边坡动力响应和稳定性分析主要依靠数值模拟、理论分析、模型试验等方法[9]。由于岩土的物理力学性质的复杂性,理论推导解决边坡动力问题很难实现,且其准确性很难得到验证[10-11]。在动力作用下,边坡土体的损伤逐渐积累并导致变形及破坏失稳,而现有的有限元软件很难模拟这一过程[12],为了更好地理解边坡在动力作用下的失稳机制,数值模拟结果还需进一步与模型试验的结果和规律进行对比。故利用振动台进行模型试验成为必要的分析手段,诸多学者借助振动台分析边坡动力响应规律已取得了很多研究成果。如徐光兴等[13]通过数值模拟和模型试验对比,讨论了地震动力作用下边坡的动力响应规律及地震动参数对边坡动力响应的影响;叶海林等[14]将振动台试验和数值模拟相结合,得出了位移和加速度响应的突变可以作为边坡动力破坏的判据依据;孙志亮等[15]借助大型振动台试验研究了不同含水率土边坡的加速度响应特征和位移发展趋势,并得出了不同含水率下边坡的加速度、位移等的响应特征;Brennan和Madabhu-shi[16]通过离心机振动台试验,定量分析坡顶加速度的放大效应;王猛等[17]采用大型振动台试验探讨了地震动力作用下隧道洞口段边坡的响应规律,以及地震动参数对动力响应的影响。在黄土动力响应方面,乔向进[18]研究了两种坡度的黄土边坡在动力作用下的响应过程,提出边坡失稳经历三个阶段;李福秀等[9]分析了两种结构的黄土边坡动力响应特征,结果表明动力作用对含裂隙边坡作用更明显;刘富强等[19-21]基于室内试验探究了不同因素对黄土动力参数的影响,得出黄土动力参数的变化规律;张泽林等[22]基于边坡的离心机振动台试验和数值模拟分析,研究地震作用下黄土-泥岩边坡动力响应特征。

反应谱是地震动分析中揭示动力响应的重要特征。自反应谱理论提出以来,学者们已经对反应谱特征进行了众多研究。其中以谢礼立等[23]为主的学者们基于现场实测数据计算了长周期的反应谱,并对其影响因素进行讨论;以徐龙军等[24]为代表的学者们对地震反应谱进行了大量理论研究。但很少有学者使用反应谱对边坡破坏机制进行研究,本文基于大型振动台模型试验,研究黄土边坡的破坏机制,根据边坡的破坏过程,分析动力模型试验中土体动力响应的反应谱变化规律。着重揭示地震动力作用下边坡的加速度动力响应特征,考虑地震动力作用下黄土边坡的变形失稳过程,为黄土区边坡的安全性评价和抗震设防提供参考。

1 振动台模型试验设计

1.1 模型设计及试验材料

试验过程中采用刚性密封模型箱,根据模型箱的尺寸对原边坡尺寸按1∶20的比例进行缩小。模型边坡尺寸:边坡底部厚30 cm、边坡坡度为30°、坡高96 cm,采用分层填筑、逐层压实的填筑方法,同时在模型边坡上布置了25个加速度监测点,模型及监测点布置示意图如图1所示。其中加速度传感器采用 DH1C301 三向电容式加速度传感器,X、Y、Z向灵敏度分别为46.3、46.2、46.0 mV/(m·s-2)[25]。

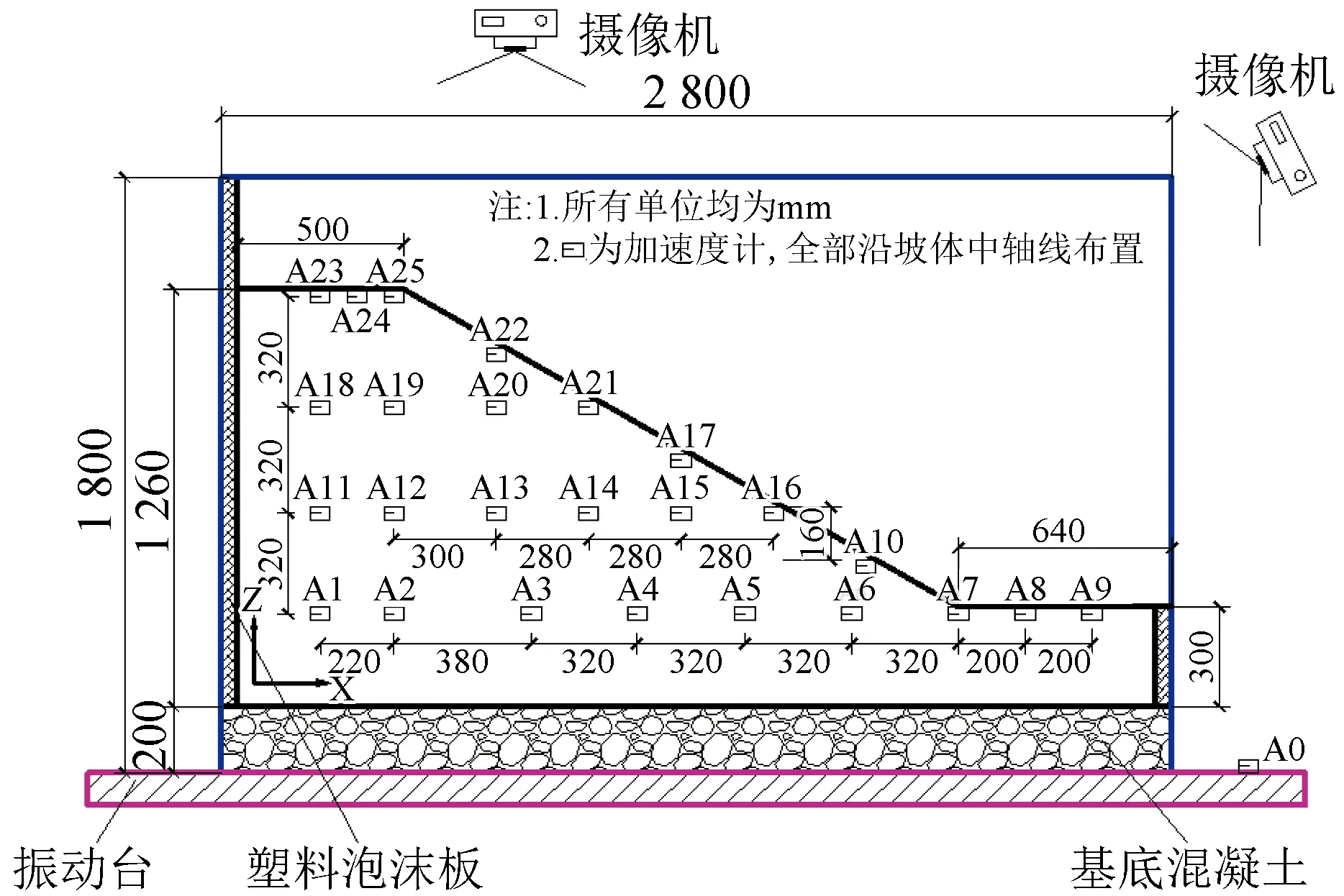
图1 边坡模型示意图(单位:mm)Fig.1 Schematic diagram of model slope (Unit:mm)

为了减小模型箱的边界效应,模型箱内壁安装了聚乙烯闭孔柔性泡沫板,箱体底部铺设了一层直径3～5 cm的鹅卵石[26],并用水泥砂浆进行了黏结,既可达到增加摩擦阻力的效果,还可模拟实际地层的基岩。根据相似理论以及量纲分析法推导,模型的相似比见表1。试验数据显示,测点4和测点7数据异常,故剔除。

表1 相似参数[18]Table 1 Similarity parameters[18]

本次模型试验用土取自兰州某地松散状Q3原状黄土,在现场用环刀取6组原状进行室内试验,以获得现场土的物理力学特性,并为相似材料的配制提供依据。

表2 试验原状土物理参数Table 2 Physical parameters of undisturbed soil used in the test

为了满足材料相似比的要求,必须对原状黄土掺加其他成分进行配制,本次试验计划掺加重晶石粉和锯末并加水配合搅拌,最终确定以原状黄土∶重晶石粉∶锯末∶水=0.835∶0.04∶0.015∶0.11的配比进行重塑黄土的配制[17],模型土体的含水率为11.4%。

表3 模型土物理参数Table 3 Physical parameters of model soil

对原状土和模型土分别进行了动三轴试验,获取到动强度参数,如表4所列。

表4 动强度参数Table 4 Dynamic strength parameters

1.2 地震输入加载方案

本次试验在中国地震局兰州地震研究所4 m×6 m大型电伺服式振动台上进行。经统计各地台站监测到的竖向加速度峰值与水平加速度峰值比为αv∶αh=0.58[27],相关规范规定竖向设计基本地震动峰值加速度均小于水平向,不论是实际监测数据还是设计标准,竖向加速度均小于水平向加速度,因此,在震动台实验的加载工况设计中,竖向加速度小于水平向加速度。输入地震加速度由弱到强,在破坏之前,主要研究模型在地震作用下的响应特征,为了最大限度利用模型,取得更多的试验数据,加载地震波采用汶川汤峪波和El-centro波两种波形交替加载,逐渐增强的方式。

地震动幅值从0.1g开始逐级施加,直至边坡破坏,共有18个加载工况(下文用GK1～GK18表示),各加载工况对应的加载波形以及输入地震波幅值情况如表5所列。

表5 输入地震波信息Table 5 Information of input seismic waves

如果根据相似性将地震波时间缩放后,试验过程太快,不便于观察破坏的过程,因此本模型试验采用实际地震波时间。其中El-Centro波卓越频率为1.25～2.5 Hz,汶川汤峪坡卓越频率为1.25～1.35 Hz,两种波加速度时程曲线和频谱图如图2所示。

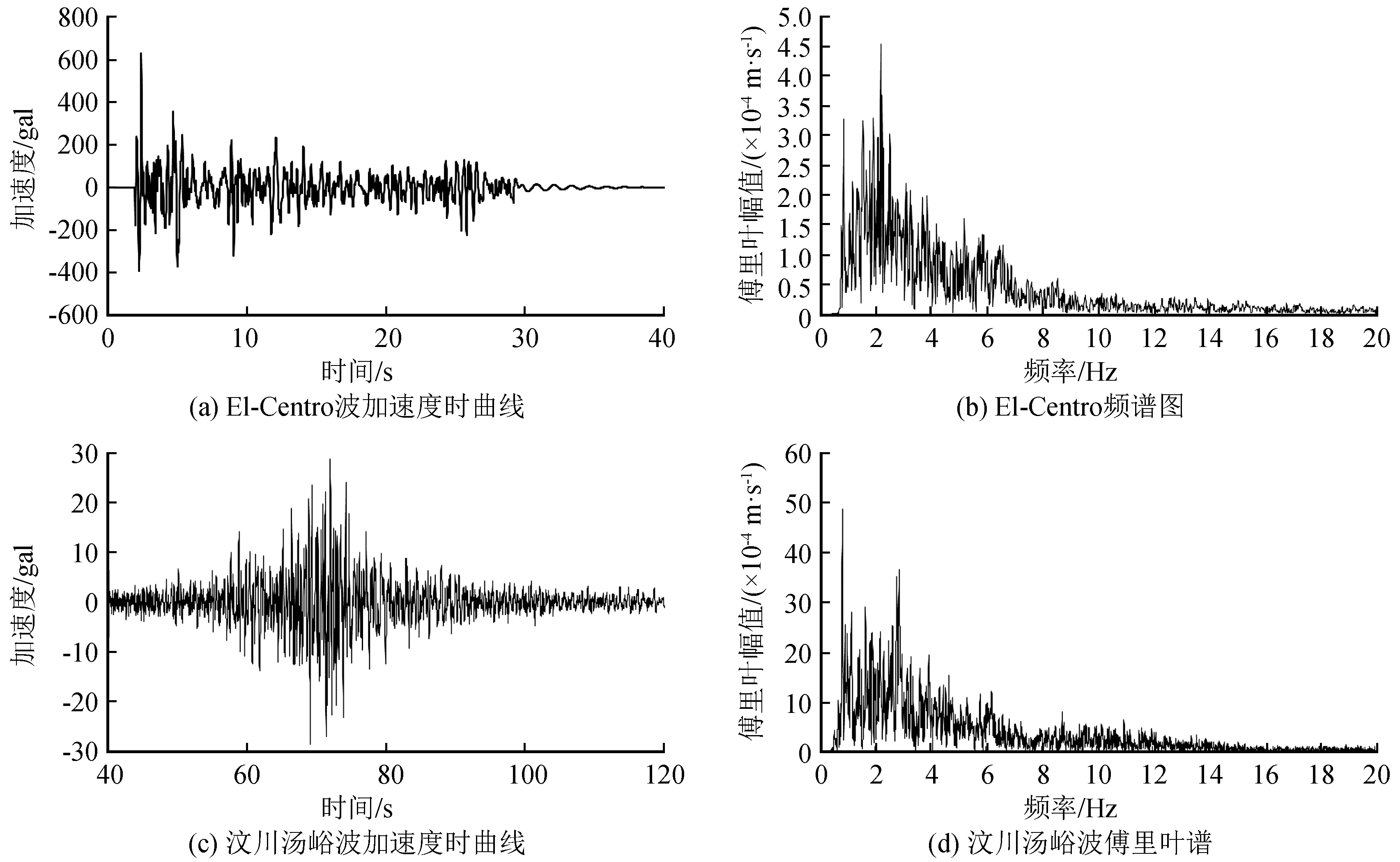
图2 加载地震波波形特征Fig.2 Waveform characteristics of seismic waves

2 加速度响应分析

2.1 边坡破坏特征

边坡破坏特点与地震输入加载方案密切相关,因此在本文中结合加载方案和试验现象对试验数据进行分析。

在实验过程中,每个工况结束后都观察坡体是否发生变化,表面是否有裂缝产生、裂缝是否贯通以及裂缝的宽度。试验过程中坡面变化情况如图3所示。

图3 加载过程中边坡破坏情况Fig.3 Slope failure during loading

为分析边坡在整个加载过程的变形失稳过程,取三组典型断面内测点进行分析,定义坡面为断面1,包括测点10、16、17、21、22、25,坡体内一竖直面为断面2,包括测点2、12、19、25,坡体内同一水平面为断面3,包括测点18、19、20、21;分别绘制三个断面测点在18个工况下的峰值加速度PGA及加速度放大系数AFA的变化规律图,以探讨边坡的破坏机制。其中柱状图代表各工况下PGA随测点的变化规律,折线图代表AFA随测点的变化规律,如图4所示。

图4 三组测点PGA及AFA随加载工况的变化趋势Fig.4 Change trend of PGA and AFA of three groups of measuring points under different loading conditions

分析PGA和AFA变化规律知,随着坡面测点高程的增加,PGA和AFA总体呈放大的趋势,在水平向上靠近坡体边缘放大效应较为显著。整体来看,随着输入地震波峰值加速度的逐级施加,三组测点加速度放大系数AFA与PGA整体呈递增的变化趋势,但在GK9、GK15加速度放大系数AFA明显变小。

试验过程中,GK1～GK8坡体未有明显破坏,在GK9加载完成后坡顶产生微小裂缝,GK15施加结束后边坡上部左右两侧出现长宽裂缝,GK17加载过程中裂缝进一步产生、扩展,边坡顶部出现大量张拉破坏裂缝,震酥现象明显;将试验现象对应AFA的变化分析如下:测点AFA发生突变的工况加载结束后,坡面均出现一定程度的破坏,综上,可将加速度放大系数的突降可以作为边坡破坏程度发生变化的判断依据。

综合试验现象与试验数据分析结果的相关性,将黄土边坡在地震动力作用下响应过程分为三个阶段:弹性变形阶段、塑性变形阶段、破坏失稳阶段。在本次试验中GK1～GK8为弹性阶段,坡体未出现明显变化;GK9～GK14为塑性阶段,坡体表面出现裂缝并进一步扩展;GK15进入破坏阶段,上部出现长宽裂缝,边坡逐步失稳,发生滑移破坏。

2.2 不同方向测点加速度响应分析

为了进一步分析放大系数的变化规律及影响因素,汶川汤峪波选取X向幅值为116 cm·s-2(GK1、GK2)与X向幅值为465 cm·s-2(GK9、GK10)等,El-Centro波选取X向幅值为117 cm·s-2(GK3、GK4)与X向幅值为470 cm·s-2(GK11、GK12)等典型工况深入分析,以探讨边坡坡面、边坡内部竖直方向与水平方向测点的加速度放大系数响应规律。

分析图5可知,在输入地震波幅值较小时,X、Z双向加载时的加速度放大系数大于X单向加载时的放大系数,两种地震波作用下,坡面以及边坡内部两个方向测点均符合该特征,说明在弱振动工况下,双向耦合波对边坡的影响较大。在输入地震波幅值较大时,汶川汤峪波显示X、Z双向加载时的加速度放大系数大于X单向加载时的放大系数,而El-centro波显示X、Z双向加载与X单向加载时的差距较小。随试验的进行,土体震酥现象更加明显,能量传递效率降低,说明在此类地震波作用下,地震动幅值较大时,双向耦合波对边坡的影响较小。

图5 不同类型波作用下坡体各测点放大系数AFAFig.5 AFA of each measuring point of the slope under different types of waves

图5显示AFA在高程上表现出非线性,随高程的增加,AFA整体呈现递增趋势,“高程放大效应”明显;在水平面内,变化规律呈“V”字型,边缘测点受边界效应与临空面放大效应的影响[13],放大系数较大。在坡面上,A16和A22侧点位于分层填筑交界面,在层与层交界处采用了刮毛处理,地震波在此处能量耗散较大,放大效应减小,在输入地震波幅值较大后(工况17、18),边坡的层间效应减小,整体性增强,A16测点与A22测点的放大效应增强。

3 反应谱分析

数据在采集过程中,由于土体波动和周围环境的干扰对数据具有一定的影响。为了消除这些影响,在试验后期处理阶段使用 SeiscomSignal 软件对所有的加速度数据进行基线校正,并对校正后的加速度波形进行0.5～25 Hz 的带通滤波。并对个别波形异常的点,进行剔除。采用校正后的加速度时程,计算得到绝对加速度反应谱,黄土的阻尼比一般在0.05左右,故阻尼比取0.05[28]。以下主要从加速度反应谱角度出发,在不改变谱线基本形状的前提下,对反应谱进行适当的平滑处理,以更好地把握变化规律。

3.1 加速度平均谱变化规律

图6表示坡体内所有测点在每个工况下的加速度平均谱,其中图6(a)表示汶川汤峪波条件下各工况测点加速度平均谱、图6(b)表示El-Centro波条件下各工况测点加速度平均谱。以汶川汤峪波为例,在弹性变形阶段,汶川汤峪波作用下反应谱主周期为0.35 s,主周期未随地震荷载逐级施加而出现变化;其中当输入地震波幅值分别为1.16 m·s-2、2.33 m·s-2时,加速度反应谱的峰值为3.50 m·s-2、7.22 m·s-2,两者相比可得:反应谱峰值增加幅度和输入的地震波幅值增加幅度的比例相一致。

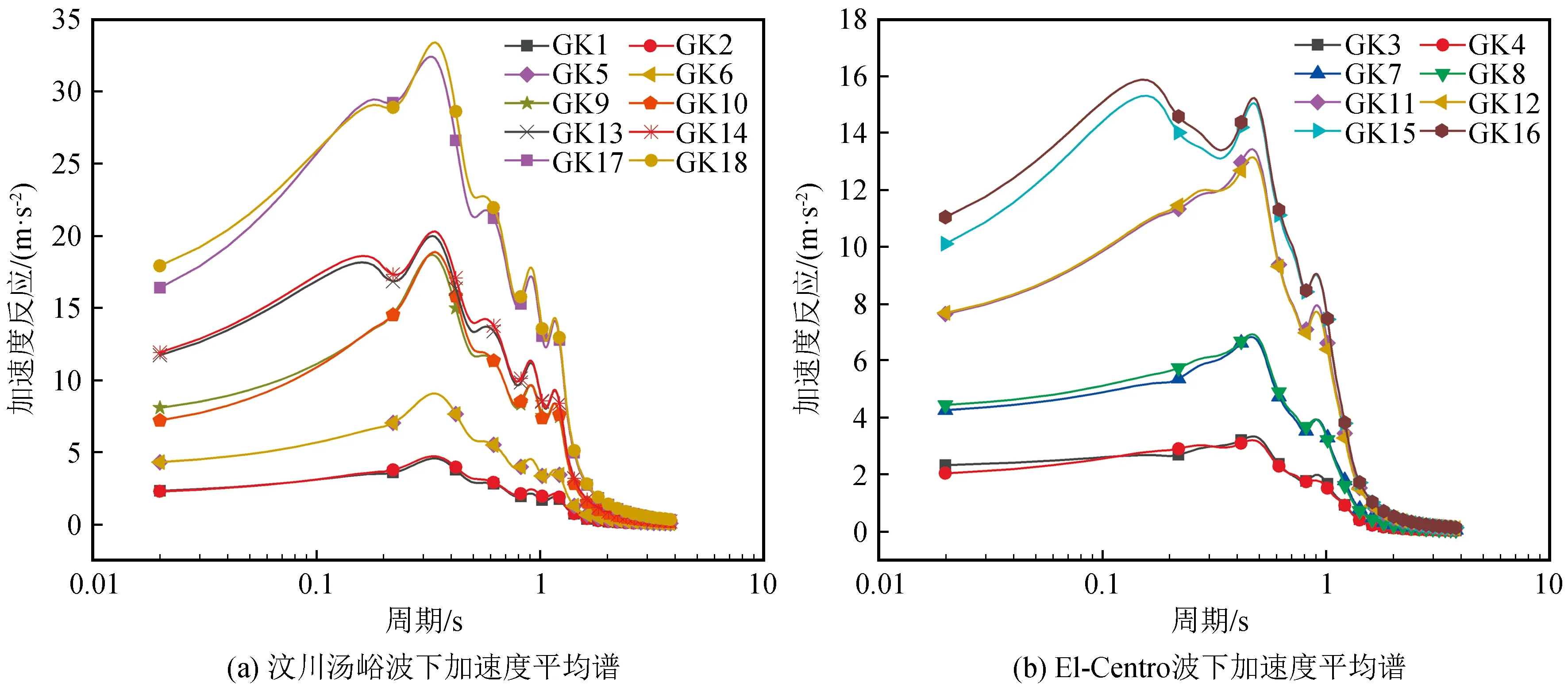
图6 加速度平均谱Fig.6 Average acceleration spectrum

在弹性变形阶段向塑性变形阶段过渡时,反应谱峰值增幅120%与实际输入的地震波幅值增幅100%相比发生突变,主周期未发生变化。进一步分析,在塑性变形阶段,GK9与GK13相比,反应谱峰值增幅与实际输入的幅值增幅相比明显变低;且在塑性阶段的后几个加载工况中,反应谱出现两个明显峰值。根据反应谱是否发生变化可以将塑性阶段划分为两个小阶段,第一阶段,反应谱未发生较大变动,该阶段坡体为内部裂隙发展阶段;在第二阶段,反应谱出现两个明显峰值,该阶段坡体内部裂隙进一步产生、发育,表面出现微小裂缝。

破坏阶段,反应谱主周期较塑性阶段发生改变,且加速度反应谱的峰值增幅相比输入地震动幅值的增幅也发生跃变。

El-Centro波作用下加速度反应谱随加载工况的变化规律与汶川汤峪波作用下加速度反应谱变化规律相同;但当输入地震动幅值相同时,El-Centro波作用下反应谱峰值较小,且主周期大。在弹性变形阶段和塑性变形阶段,两种波的XZ双向耦合波与X单项波的相比,峰值和主周期的变化极小。

3.2 频谱解释

为了进一步研究边坡破坏机制和反应谱变化规律,选取典型工况下典型断面内测点加速度反应谱进行分析。El-Centro波与汶川汤峪波具有相似的变化规律,图7、图8主要以水平(X)输入的汶川汤峪波为例,分析反应谱形状发生的变化,其中图7表示坡面、竖直面内测点在不同工况下的反应谱,图8表示距坡顶1/3处水平面内监测点与距坡顶2/3处水平面内监测点在不同工况下的反应谱。

由图7可以看出,反应谱峰值波动趋势与加速度放大系数的变化规律具有一致性。在小于主周期的周期内,反应谱存在两个明显峰值,且随输入地震波幅值增加,反应谱首峰越来越明显。在同一幅值条件下,中上部测点首峰较为凸显;在不同幅值条件下,中上部测点首峰出现的时间比下部测点首峰出现的时间早。当输入加速度为698 cm/s2时,上部测点首峰对应的周期成为该处测点的主周期,但下部测点主周期改变有一定的滞后性。

由图8可知,在离坡顶1/3处的水平面内,坡体边缘测点加速度反应谱较大,离坡顶2/3处的水平面内,坡体边缘侧点加速度反应谱较小,因此,测点加速度反应谱受高程影响大,且边界效应和临空面对反应谱的影响较为显著。越临近坡面,即随宽度增加,反应谱首峰越来越凸显。同一水平面内的不同测点,首峰出现的时间和主周期发生改变的工况具有一致性;不同高程处的平面相比,首峰和主周期的变化规律符合图7中所呈现的规律。

图7 X向汶川汤峪波作用下断面1、断面2内各测点加速度反应谱Fig.7 Acceleration response spectrum of each measurement point in section 1 and section 2 under the action of X-direction Wenchuan Tangyu wave

图8 X向汶川汤峪波作用下两组水平面内各测点加速度反应谱Fig.8 The acceleration response spectrum of each measuring point in the two horizontal planes under the action of X-direction Wenchuan Tangyu wave

结合前面分析可知:

(1) 主周期的改变,标志着坡体进入破坏阶段;而且首峰对应的周期恰为主周期发生改变后的主周期,因此首峰的凸显程度(首峰和主峰峰值之差与主峰峰值之比)可以作为边坡破坏程度的判断依据。

(2) 坡体中上部较先进入下一阶段,下部滞后上部1～2个加载工况,故使用整体平均谱变化规律可以分析边坡破坏机制,但有一定的局限性。

(3) 越靠近边坡中上部,测点受高程放大效应与临空面放大效应的影响越大,且失稳的可能性越大。