基于滤波函数的风电并网逆变器改进线性自抗扰控制

周雪松，张波，马幼捷

(天津理工大学 电气电子工程学院，天津 300384)

0 引 言

并网逆变器作为风电系统中的重要环节，随着风电系统装机容量的激增，对并网电能质量的要求也越来越高，控制技术在其中起到了关键作用[1]。同时，系统输出的量测环节会引入大量噪声，例如，高频开关所带来的噪声污染，某些情况下电力线路对测量信号产生的工频干扰信号等，这些使传统的PI控制难以满足高性能需求[2]。

自抗扰控制 (Active Disturbance Rejection Control，ADRC)是一种新型控制算法，它将被控对象中的无法建模部分和未知扰动都认为是系统扰动，通过扩张状态观测器(Extended State Observer，ESO)进行估计，并在反馈中补偿掉，对非线性、多变量、强耦合的系统具有较好的控制效果[3-4]。但是在最初的ADRC中，ESO和误差反馈控制率这两个元素是以非线性函数形式呈现的，整定的参数较多，不便于实际应用中进行调试。对此高志强教授将以上两个环节线性处理，提出了线性自抗扰控制(LADRC)，并利用带宽确定控制器参数，使得整个系统易于调试和实际应用[5]。尽管LADRC具有较强的抗扰性和跟踪性，LESO较大的增益系数也会带来噪声放大问题,进而影响控制器的稳定性[6]。为解决LESO的噪声敏感特性，国内外学者提出了许多不同的解决方案，文献[7]采用了切换LESO增益的方法，研究表明改进型LADRC能够迅速估计系统状态，同时有效抑制输出端的测量噪声。文献[8]提出了一种自适应可变增益的观测器来抑制噪声对系统的影响，并保证不改变LESO的原本特性。虽然以上方案能够较好的抑制噪声的影响，但是设计比较复杂，工程应用困难。文献[9]提出了一种预报跟踪微分自抗扰控制器，能够抑制噪声影响，并减小相位延迟，但存在动态性能变差，参数整定困难的问题。文献[10]将滤波器方程扩展到ESO中，较好的解决了输出噪声对系统的影响，但文中使用了非线性ADRC，参数整定比较困难。

文中将滤波方程与二阶LADRC相结合，构造基于滤波函数改进型LADRC，并对改进型LADRC进行了抗扰、噪声抑制和稳定性方面的分析，在保证系统稳定的前提下，能够对噪声进行有效的抑制。最后通过仿真，验证控制策略的可行性。

1 并网逆变器数学模型

图1为风电并网逆变器系统结构图。

假定电流参考方向为电网流入逆变器方向，根据基尔霍夫定律，建立数学模型：

(1)

式中ea，eb，ec为电网电压；ia，ib，ic为电网电流；ua，ub，uc为三相网侧逆变器输出电压；L为等效的滤波电感；R为等效的电阻；Udc为直流母线电容电压；idc为直流侧输出电流；Sa，Sb，Sc分别为各相桥臂的开关函数。定义开关函数：

(2)

式中k=a，b，c。

由于三相电流互相耦合，不利于控制器的设计，因此采用坐标变换的方法，把数学模型变换到dq旋转坐标系下，得到并网逆变器在dq坐标系中的数学模型：

(3)

式中ed，eq为电网电压在旋转坐标系dq轴的分量；id，iq为电网侧电流dq轴的分量；ud，uq为电网侧逆变器输出相电压在旋转坐标系dq轴的分量；Sk为开关函数dq轴的分量；ω为电网角频率。

2 传统LADRC控制器

LADRC是由线性跟踪微分器(Linear Tracking Differentiator，LTD)、线性扩张状态观测器(LESO)、线性状态误差反馈率(Linear State Error Feedback，LSEF)三部分构成，如图2所示。

LTD的作用是提取微分信号，实现快速无超调的跟踪输入信号[11]，文中为避免使用跟踪微分器造成电容电压高频次震荡，因此不采用跟踪微分器。

图2中，y为系统输出，u为控制器输出，z1，z2，z3为观测器对系统各个状态变量和总扰动的观测值，v是参考输入，b0是控制器增益。

由于被控对象为二阶系统，因此设计二阶LADRC控制器。控制策略采用电压矢量定向控制，并设置q轴电流为零，因此式(3)可以转变为：

(4)

根据式(4)可以得到下列形式的状态空间方程：

(5)

式中x1、x2分别为直流母线电压及其微分；x3为新扩张的一个状态变量，代表系统的总扰动，记为f。其中，h为总扰动的微分，b0=3/(2LC)。由式(4)可以将总扰动记为：

(6)

根据式(5)可以构建三阶LESO：

(7)

式中z1、z2、z3分别为直流母线电压、直流母线电压微分和总扰动的观测值；β1、β2、β3为观测器增益。选取合适的β1、β2、β3，LESO将实现对式(5)中的各状态变量的实时跟踪，即z1→x1、z2→x2、z3→x3。

LESF设计为：

u0=kp(v-z1)-kdz2

(8)

式中kp、kd为控制器参数。并取扰动补偿环节为:

(9)

此时，若忽略z3和f之间的误差，式(5)可简化为积分串联型结构。根据文献[5]极点配置法，可以做如下的极点配置：

(10)

(11)

式中ωo，ωc分别为观测器和控制器的带宽，通过上述极点配置，LADRC只需调节b0，ω0，ωc三个参数。

3 改进型LADRC结构设计

3.1 传统LADRC控制器存在的问题

根据式(7)、式(10)可以得到z1、z2、z3的传递函数：

(12)

(13)

(14)

文献[12-14]证明了传统LESO具有良好的抗扰性和收敛性。若考虑输出y的噪声δ对三阶LESO的影响。由式(12)可以得到噪声的传递函数：

(15)

取ωo=10、20、30、40、50可以得到式(15)的频域特性曲线。

从图3中可以看出，随着ωo的增加，高频带增益增加显著，同时对噪声的放大效果越明显。

图3 观测噪声的频域特性曲线

LESO虽然具有较强的抗扰能力，但是，由于控制器增益取的值比较大，它对噪声比较敏感。实际工程中存在很多噪声污染，如果不加处理，轻则会引起系统输出抖振，减少执行机构的寿命；严重情况下，会降低控制器稳定性。因此，系统输出被噪声污染情况是必须考虑的问题。

3.2 改进型LADRC设计

假设被控对象输出端含有测量噪声δ，即y=x1+δ。为减少输出端噪声，将母线电压信号滤波后作为控制器的反馈输入，定义滤波后状态变量为x0,则:

(16)

式中T为时间常数；ω为一阶低通滤波器的截止频率，ω=1/T。

联立式(5)、式(16)，系统的状态方程变为:

(17)

式中y0为滤波之后系统的输出，此时，输出不含高频噪声，消除了噪声对控制器的影响。对式(17)可以构建4阶LESO。

(18)

式中β0、β1、β2、β3为观测器增益；z0为x0观测值。定义e0=z0-y0，e0为LESO对y0的观测误差。选取合适的观测器增益可以实现对系统的噪声抑制与扰动补偿。

根据文献[5]的极点配置方法，让式(18)的特征方程为理想的形式，以实现对参考信号快速且无超调的跟踪，则有：

(19)

由此可得出改进型LADRC如图4所示。

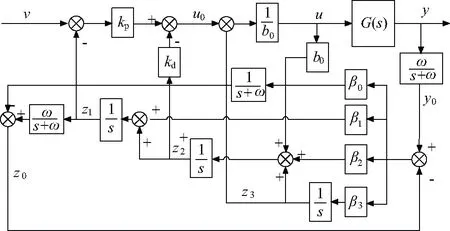
图4 改进型LADRC结构图

4 改进型LADRC性能分析

4.1 改进型LESO收敛性与估计误差分析

由式(18)和式(19)可得改进型LESO观测值的传递函数分别为:

(20)

(21)

(22)

(23)

令跟踪误差e1=z1-x1.e2=z2-x2，可得：

(24)

(25)

(26)

令e3=z3-f，又根据式(17)可以得到f=x3=x1-b0u，则：

b0u+s2δ(s)

(27)

考虑到分析的典型性，y0，u均取幅值为K的阶跃信号y0(s)=K/s，u(s)=K/s，求得稳态误差：

(28)

式(28)表明,改进型LESO具有较好的收敛能力和跟踪能力,并且能够满足对系统状态变量与扰动的无差估计，并不受系统噪声的影响。

4.2 改进型LADRC抗扰性能和噪声抑制能力分析

4.2.1 改进型LADRC控制系统的闭环传递函数

由式(8)、式(9)、式(11)可得：

(29)

代入式(20)～式(23)可得：

(30)

式中:

根据式(30)可以得到系统的简化结构如图5所示。

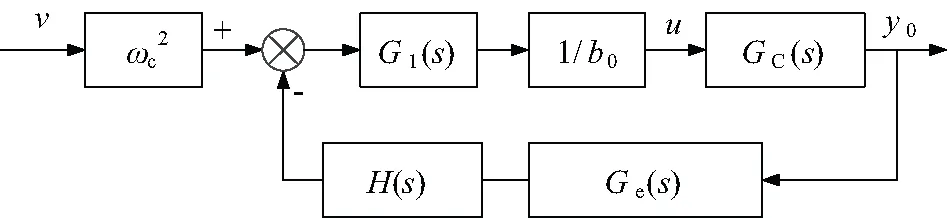
图5 简化系统结构图

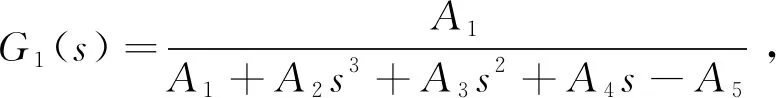
结合式(17)，可将被控对象记为：

(31)

由图5可得系统输出的闭环传递函数为：

(32)

由式(32)可知，系统输出由跟踪项、扰动项和噪声项组成，当忽略扰动项和噪声项时，系统输出只含跟踪项。取一阶低通滤波器的截止频率ω为定值。此时系统控制性能只由控制器带宽ωc决定，控制器带宽越大，跟踪速度越快。

4.2.2 改进型LADRC与传统LADRC对比分析

图6为改进型LADRC与传统LADRC扰动传递函数幅相曲线对比，可以看出，改进型LADRC的系统高频段增益减小，抗扰性增强。同时，系统也会出现相位滞后的情况。

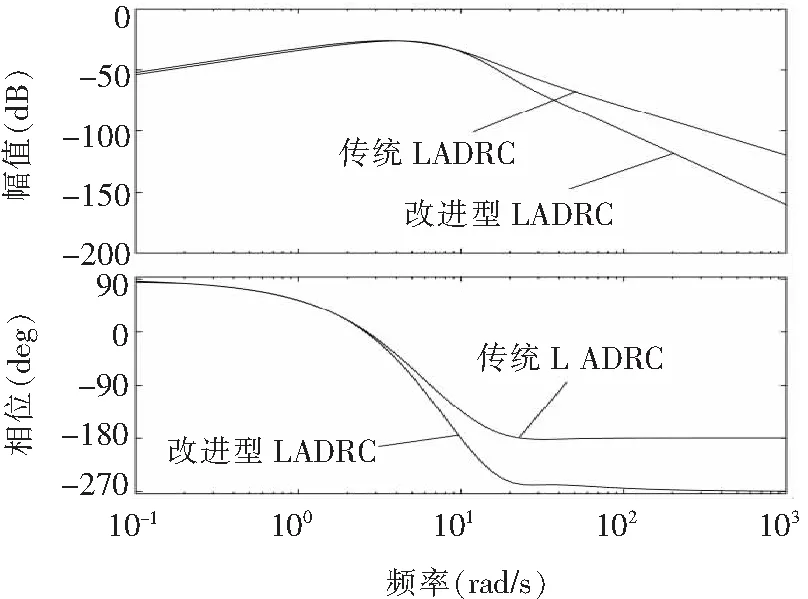
图6 改进型LADRC与传统LADRC扰动幅相曲线

图7为改进型LADRC与传统LADRC噪声传递函数幅相曲线对比，可以看出，改进型LADRC的噪声抑制能力明显增强，对噪声的跟踪能力也优于传统LADRC。

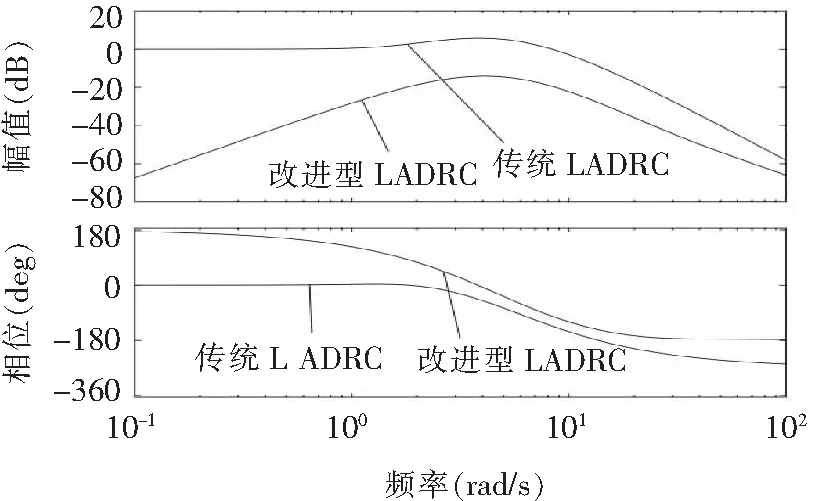
图7 改进型LADRC与传统LADRC噪声幅相曲线

5 改进型LADRC稳定性分析

根据图8可得实际系统的闭环传递函数为：

(33)

由式(29)及式(33)可得：

(34)

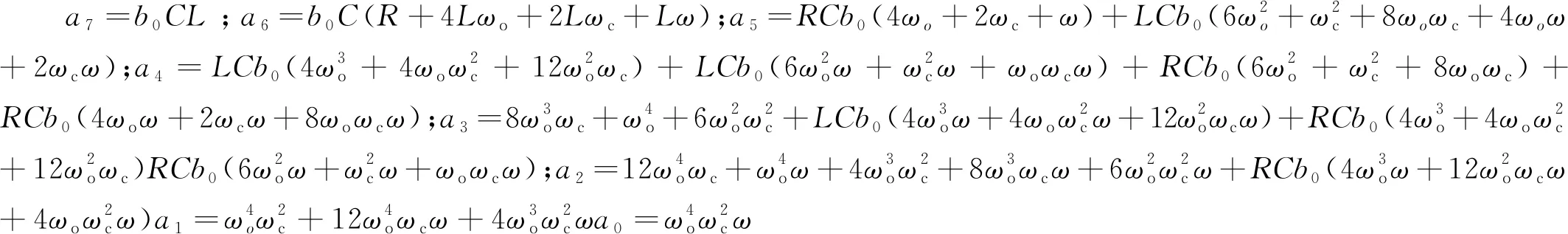
由于，ωo、ωc和ω均为正，因此，ai>0，i=0,1,2，3，4，5，6，7。

判断系统运行是否稳定可通过李纳德-戚帕特代数稳定判据进行判定，即偶数阶或奇数阶赫尔维兹行列式为正则系统稳定。由式(34)可知，Δ3>0,Δ5>0,Δ7>0。综上所述，改进型LADRC具有较好的控制性能。

图8 改进型LADRC并网逆变器系统结构

6 仿真研究

本文基于MATLAB仿真软件，搭建了1.5 MW永磁直驱风电机组模型，以进一步验证改进型LADRC的可行性。系统和控制器具体参数见表1和表2。

表1 并网逆变器参数

6.1 抗扰能力仿真分析

为了比较传统LADRC与改进型LADRC控制下直流母线电压的抗扰能力，文中设置了电网电压对称跌落30%和电网电压对称跌落50%两种故障，直流母线电压波形分别如图9、图10所示。图9对应电网电压对称跌落30%的直流母线电压波形，可以看出在故障瞬间，改进型LADRC控制直流母线电压的超调幅值，相对于传统ADRC，减小了1.2 V；在故障恢复瞬间，改进型LADRC控制直流母线电压的跌落幅值，相对于传统ADRC，减小了0.7 V。图10对应电网电压对称跌落50%的直流母线电压波形，可以看出在故障瞬间，改进型LADRC控制直流母线电压的超调幅值，相对于传统ADRC，减小了3.8 V；在故障恢复瞬间，改进型LADRC控制直流母线电压的跌落幅值，相对于传统ADRC，减小了3.6 V。以上仿真表明，相比于传统LADRC，改进型LADRC的抗扰能力有一定程度的提高。

表2 控制器参数

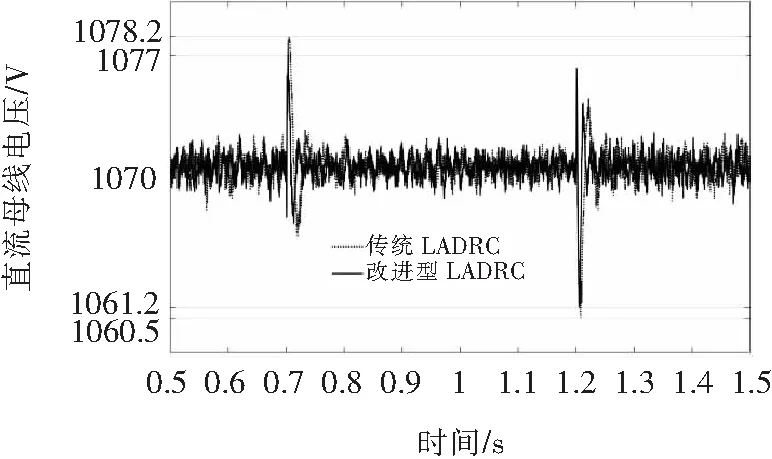
图9 电网电压跌落30%直流母线电压波形

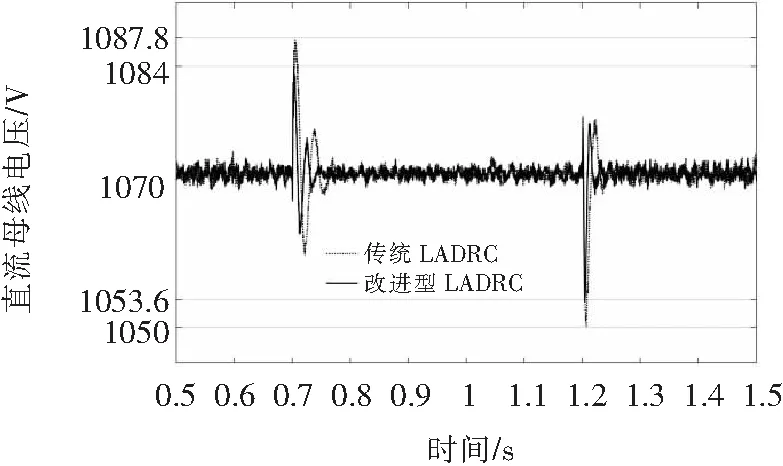
图10 电网电压跌落50%直流母线电压波形

6.2 噪声抑制能力

为了比较传统LADRC与改进型LADRC控制下系统的噪声抑制能力，文中在直流母线电压上加入了相同的白噪声。图11为受到噪声影响时，传统LADRC和改进LADRC控制下直流母线电压仿真波形对比。图12、图13为存在噪声污染时传统LADRC和改进型LADRC控制下的电网电压波形。图13、图14为噪声污染时传统LADRC和改进型LADRC控制的并网点电压频谱图。

图11 直流母线电压波形

图12 传统LADRC控制的并网电压波形

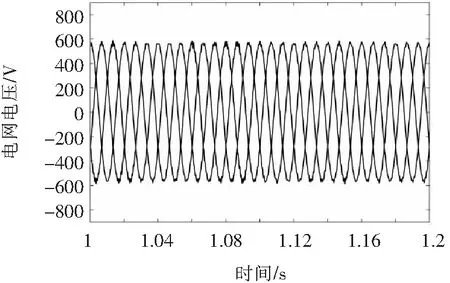
图13 改进型LADRC控制的并网电压波形

图14 传统LADRC控制的并网电压频谱图

由图11可以看出，传统LADRC控制的直流母线电压稳态时的波动范围为1 046 V～1 097 V，改进型LADRC波动范围为1 059 V～1 083 V，因此，传统LADRC会使直流母线电压产生较大震荡，改进型LADRC能够明显抑制噪声对系统的影响。由图12、图13可以看出，传统LADRC控制的并网逆变器在受到噪声影响时，并网电压波形会出现严重的失真，而改进型LADRC控制的并网逆变器在受到噪声影响时，并网电压波形的正弦度大大提高，接近于正弦波。由图14、图15可以看出，在采用改进型LADRC控制时，并网电压的谐波畸变率由17.96%降为2.58%，达到了谐波抑制国家标准。通过以上仿真表明，改进型LADRC控制明显的改善了系统在噪声污染时的性能。

图15 改进型LADRC控制的并网电压频谱图

7 结束语

文章针对风电并网逆变器直流母线电压量测环节易受噪声污染的问题，设计了一阶低通滤波函数与自抗扰控制器相结合的改进型线性自抗扰控制器，并通过理论和仿真对所提出的控制策略进行了分析。研究结论如下：(1)改进型自抗扰控制具有较好的抗扰和稳定特性；(2)改进型自抗扰控制能够有效抑制噪声污染对系统的影响，降低传统自抗扰控制对噪声污染具有放大作用的问题；(3)改进型自抗扰控制会对系统输出造成相位滞后现象，未来的研究可以在这一方面做进一步的工作。