内置有水平挡板的矩形储液器非线性晃动分析

2022-10-11钟文坤吴玖荣傅继阳孙连杨

工程力学 2022年10期

钟文坤，吴玖荣，傅继阳，孙连杨，黄鹏

(广州大学风工程与工程振动研究中心，广州 510006)

部分充液储液器内液体的晃动常见于航空航天、海洋船舶及液罐车等领域，在较大外激励作用下，储液器内液体会出现明显的非线性晃动现象。液体的非线性晃动包含非常复杂的动力学机理[1-4]，不同模态之间相互耦合，高阶模态被激发，使得高阶模态对液面波高的贡献成分变大甚至超过最低价模态，进而也导致了线性模态理论的失效。储液器内液体发生非线性晃动后，会对储液器内壁产生较大的压力及作用力矩，严重影响结构的稳定性和安全性，因此，进一步了解储液器内液体的非线性晃动特性有着重要的意义。

对于储液器内液体的非线性晃动问题，已有大量学者进行了研究。FALTISEN 等[5-6]利用Bateman-Luke 变分原理和模态方法推导了液体非线性晃动的模态方程，并利用该模态方程研究了二维矩形储液器内液体晃动的非线性问题。LOVE 等[7]利用FALTISEN 等的理论研究了内置有格栅的二维矩形储液器内液体的非线性晃动，结果表明：考虑三阶与五阶模态方程组合得到的液面波高、晃动力基本一致，且与试验值较接近，而线性解却明显低估了液面波高；同时他还研究了内置有十字柱的二维矩形储液器内液体的非线性晃动，并利用振动台试验进行了验证，结果表明：利用多维模态方程求解的值与试验值较接近[8]。李遇春等[9]利用FALTISEN 等的理论进一步研究了二维矩形储液器分别在地震激励、水平简谐激励、竖向简谐激励下液体的非线性晃动响应，结果表明：多模态方法在求解长时间非线性响应分析上具有较好的优势。GURUSAMY 等[10]利用试验研究了浅水水箱在不同水深比、长宽比、激励幅值及激频比下液体的非线性晃动问题；YAN 等[11]采用基于速度势的Boussinesq方程求解了浅水矩形水池中的三维非线性晃动运动问题，并利用数值模拟进行了验证；XIN 等[12]基于笛卡尔网格的三维多相流模型，利用数值方法研究了带或不带挡板的棱柱形储罐中的大振幅晃动问题。余延生等[13-14]把FALTISEN 等的理论进一步应用到求解二维圆柱形储液器液体的非线性晃动问题，并利用渐进关系把无穷维的模态系统降价为五维的模态系统，结果表明：利用五维模态方程求解后得到的液面波高与实验结果较吻合。张海涛等[15]针对矩形储液器的非线性晃动问题，提出了一种基于有限差分算法的数值模拟方法，结果表明：该方法具有较好的收敛性和准确性；同时，他还利用振动台试验研究了矩形储液器内液体非线性晃动的拍振和共振问题[16]。王佳栋等[17]基于流体子域法建立了流体非线性晃动的无穷模态系统，并通过模态渐进关系得到有限维的模态系统，最后利用有限维模态系统研究了地震激励下带有多层刚性隔板圆柱形储液器内液体晃动的非线性响应，结果表明：防晃板的设计不能忽略液体晃动非线性效应。

为减小储液器内液体的非线性晃动响应，可在储液器内部安装水平挡板、竖直挡板、格栅及立柱等耗能装置[18-19]。该类装置可有效提高储液器的阻尼，进而可有效抑制液体的晃动。尽管已有大量的学者对储液器内液体的非线性晃动进行了研究，储液器的减晃工作也得到进一步完善，但仍存在以下两方面不足：一方面，对于水平挡板类的耗能装置，由于其制作简单且便于安装，被广泛应用于储液器的减晃，但在利用多模态方程研究储液器的非线性晃动响应过程中，基本都忽略了挡板所提供的附加非线性阻尼项；另一方面，储液器内安装了耗能装置后，会给储液器带来附加质量，附加质量会降低储液器的晃动频率，也会影响阻尼比估算公式的准确性。附加质量的定义为：与淹没或者部分淹没的结构元件一起运动的水所夹带的质量，一般由势流理论来确定[20]。

基于此，本文以内置有水平挡板的矩形储液器为研究对象，利用势流理论、虚功原理推导了由水平挡板所提供的非线性阻尼比表达式，同时考虑水平挡板对储液器晃动频率的影响对非线性阻尼比进行了修正，再利用FALTISEN 等的非线性模态理论，研究了不同水平挡板位置、长度下储液器内液体的非线性晃动响应特性，并利用Fluent软件进行数值模拟，并与理论模型的分析结果进行对比。

1 非线性阻尼比推导

1.1 流体势流理论

以矩形储液器为研究对象，假定储液器安装有多块水平挡板，且只考虑x、z两个方向，如图1所示。图1 中：h为储液器静止水深；L为长度；lb为水平挡板长度；zi为水平挡板位置；η(x,t)为液面晃动波高。

1.2 虚功原理

ζn为非线性阻尼比，表示为：

2 非线性晃动三阶模态方程

本节采用FALTINSEN 等[5]推导的二维矩形储液器非线性晃动三阶模态方程，该篇文献中所推导的某些方程系数存在错误，但在他的著作《Sloshing》[24]中已经进行了更正，所以以下所给的方程系数是已经更正的系数[24]：式中，X¨为储液器底部的加速度激励，该方程并未考虑储液器中阻尼项的影响，而对于安装有水平挡板等耗能装置的储液器，其阻尼由液体的粘滞阻尼及耗能装置所提供的阻尼两部分组成。与耗能装置所提供的阻尼相比，由水的粘性所提供的阻尼较小，可忽略不计，但对于小缩尺比的储液器，水的粘滞阻尼影响却比较大[23]，为提高理论的估算效果，把水的粘滞阻尼值一并计入储液器的总阻尼值中。考虑阻尼项的储液器非线性晃动三阶模态方程为：

式中：ν为水的粘度；b为储液器的宽度；SC为水的表面光滑因子，通常取1。

把式(24)转化为标准的一阶常微分方程组后，再用Runge-Kutta 法进行求解，求解后的值代入式(6)可得到矩形储液器的液面波高，储液器晃动力的计算公式为[7]：

3 液体晃动的数值模拟

为验证上述理论模型的可靠性，本节利用Fluent 软件进行数值模拟，对应的矩形储液器储液器模型如图2 所示。计算过程中，采用VOF 多相流模型来追踪自由液面波高，模型受到的底部激励为正弦加速度激励y=ω2X0sin(ωt)，X0为激励幅值，通过UDF(用户自定义函数)施加，方向为沿储液器长度方向。模型的尺寸为：0.6 m (长)×0.375 m (宽) ×0.8 m (高)，在左右侧壁对称安装单块水平挡板。采用的有限体积法模型的网格尺寸大小为2 mm，时间步长为0.002 s，分别在储液器中设置不同的水平挡板位置、长度进行仿真计算，具体见表1。

图2 矩形储液器模型Fig. 2 Rectangular storage tank model

表1 数值模拟工况Table 1 Parameters in numerical simulation

本文选择用Fluent 软件进行数值模拟的目的，是进一步以验证理论模型的准确性，考虑到试验过程中，水平挡板的安装及固定并非是一件易事，特别对于长度较长的水平挡板。为验证数值模拟结果的准确性，以安装有单块垂直挡板的矩形储液器为例(垂直挡板在储液器中部)，利用振动台试验进行验证，振动台试验装置如图3 所示。试验储液器的尺寸大小为0.62 m(长)×0.395 m(宽)×0.81 m(高)，由有机玻璃制作而成，厚度为1 cm；试验中的垂直挡板也为有机玻璃制作而成，厚度为0.8 cm。水的晃动波高利用电容式数字波高仪采集，采样频率为100 Hz，放置在距储液器左侧壁1 cm 处。储液器的基底剪力采用由瑞士KISTLER公司生产的剪力传感器测量，一共4 个，剪力传感器测得的值包括两部分：TLD 矩形储液器中水的晃动所产生的剪切力；台面连接构件及储液器本身所产生的惯性力。因此，剪力传感器测量值需减去惯性力才能得到TLD 矩形储液器的晃动力。振动台对储液器施加的激励为正弦激励，试验工况见表2，lb为垂直挡板的高度。

图3 振动台试验装置Fig. 3 Shaking table test

表2 试验工况Table 2 Parameters in Experiment

限于篇幅，以下只给出如图4 所示的工况对比图，由图4 可知，采用数值模拟得到的储液器液面波高、晃动力与振动台试验测量结果较接近，具有较好的模拟效果。因此，本文所采用的数值模拟方法具有较好的精度，可利用数值模拟来验证理论模型的准确性。

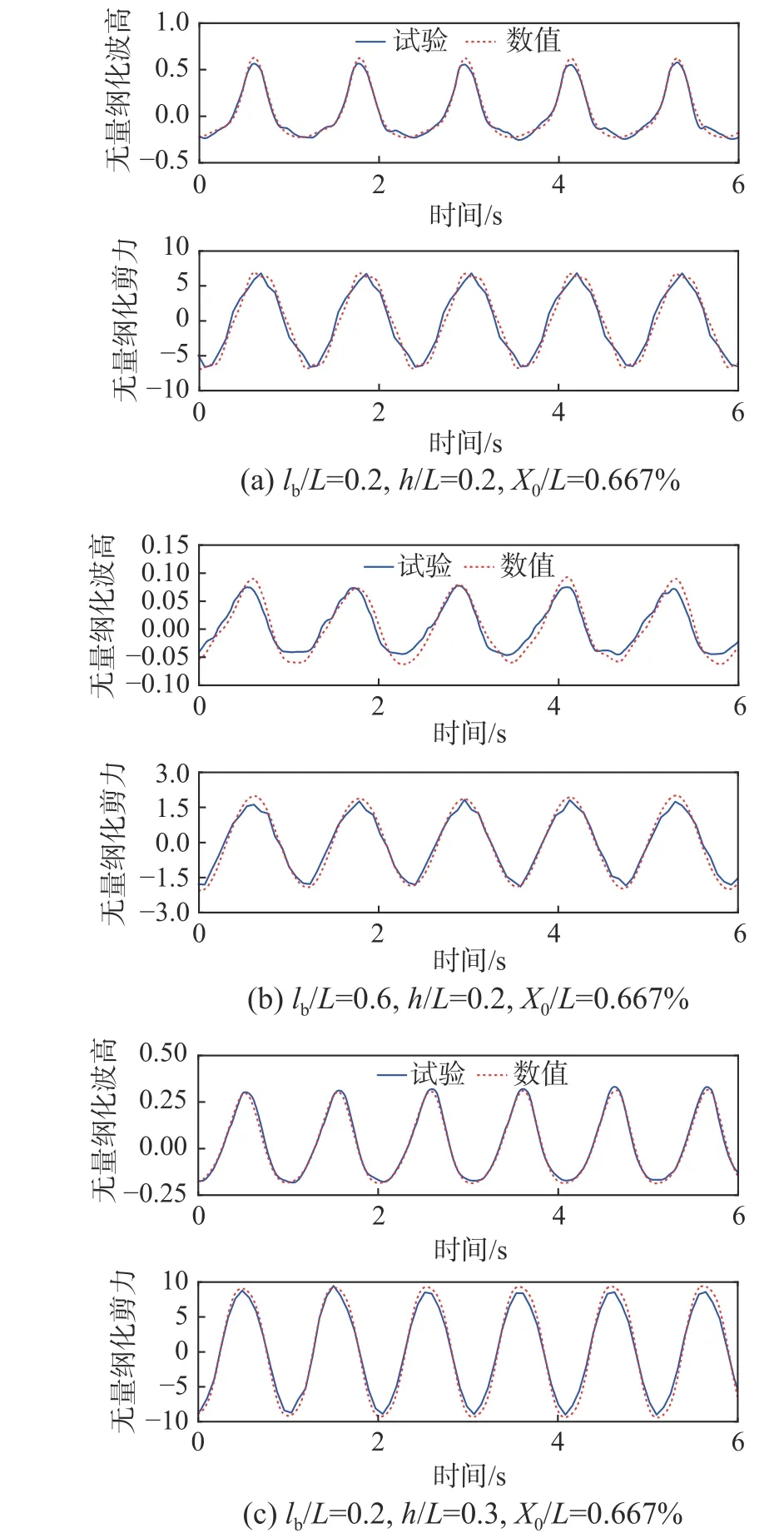
图4 试验与数值模拟对比Fig. 4 Comparison between experiment and numerical simulation

4 结果分析

本节分别给出储液器侧壁液面波高、晃动力的理论值与数值模拟值对比图。为避免缩尺效应影响，波高与晃动力分别采用如下方法进行无量纲化处理：

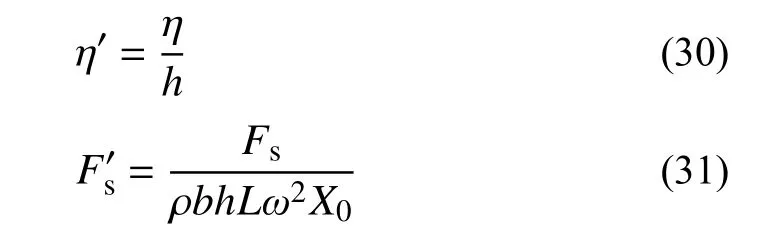
4.1 水平挡板位置对储液器晃动特性影响

限于篇幅，图5 只给出水平挡板位置zi/h分别在0.1、0.3、0.5、0.7、0.8 及0.9 下储液器侧壁液面波高与晃动力的理论值与数值模拟值对比图。由图5 可知，水平挡板位置小于0.5h时(即靠近于储液器底部)，液体非线性晃动现象较明显，利用非线性三阶模态方程得到的波高、晃动力与数值模拟结果较接近，而仅采用一阶线性的贡献时，却明显低估了储液器液面波高，但求解的晃动力却与非线性值基本一致。这表明，即使储液器液体在非线性晃动下，采用线性理论模型计算晃动力也能获得较好的预测效果，可从式 (26)中解释这一现象。在给定底部加速度激励作用下的模态响应βn(t)，较高阶奇数模态对储液器总晃动力的贡献较小[8]，而偶数阶的模态对储液器总晃动力不起贡献作用，所以采用线性模态理论也能较好地预测储液器晃动力。随着水平挡板到自由液面的距离逐渐变小(即越来越靠近自由液面)，其提供的阻尼比也增大，液体晃动呈线性变化。当水平挡板位置大于0.9h时，即靠近于自由液面，采用非线性模型计算的液面波高与晃动力明显低于数值模拟结果，此时非线性模型失效。这是因为水平挡板靠近自由液面时，对液体的晃动运动趋势影响较大，能明显的改变液体流动方向。

图5 波高、晃动力的理论值与数值模拟值对比(挡板位置变化)Fig. 5 Comparison in the wave heights and sloshing forces between analytical and numerical simulation results (with variation in baffle location)

图6 给出了不同水平挡板位置下储液器液面波高与晃动力对比图(数值模拟值)，由图6 可知，随着水平挡板逐渐靠近自由液面，液面波高与晃动力幅值减小，这说明水平挡板越靠近于液面，对液体晃动的抑制效果越明显。表3 详细地给出了不同水平挡板位置下储液器的晃动频率值，从表中可以发现，随着水平挡板到自由液面距离的减小，储液器晃动频率也逐渐减小，减小幅度最大值可达5.7%。这说明，当水平挡板较接近于液面时，对储液器晃动频率影响较明显，不能忽略，而利用式(20)进行修正后的晃动频率与数值模拟测得的值较接近，能获得较好的预测效果。

表3 水平挡板位置变化对储液器晃动频率影响(lb/L=0.1)Table 3 Effect of the horizontal baffle location on water sloshing frequency in storage tank (lb/L=0.1)

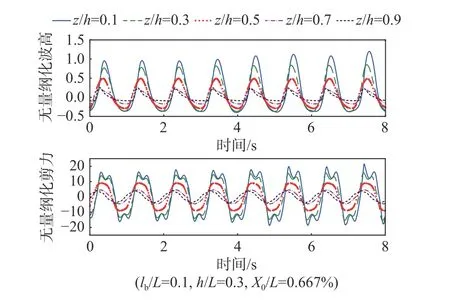
图6 不同水平挡板位置下液面波高与晃动力对比图(数值模拟值)Fig. 6 Variation in wave height and sloshing force with the location of horizontal baffles

4.2 水平挡板长度对储液器晃动特性影响

限于篇幅，图7 只给出水平挡板长度lb/L为0.05、0.15、0.25 及0.3 工况下储液器液面波高与晃动力的理论值与数值模拟值对比图。由图7 可知，水平挡板长度小于0.15L，液体非线性晃动现象比较明显，利用本文的非线性理论模型得到的计算结果与数值结果较接近，能获得较好的估算效果，而线性理论同样会低估了液面波高，但晃动力值却仍与非线性值接近，原因同4.1 节所述一致。随着水平挡板长度增大，液体晃动逐渐呈线性变化，非线性值与线性值都与数值结果较接近，能获得较好的预测效果。

图7 波高、晃动力的理论值与数值模拟值对比(挡板长度变化)Fig. 7 Comparison in the wave heights and sloshing forces between analytical and numerical simulation results(with variation in baffle length)

图8 给出了不同水平挡板长度下储液器侧壁液面波高与晃动力对比图(数值模拟值)，由图可知，随着水平挡板长度增大，液面波高与晃动力幅值减小，液体呈线性晃动，说明水平挡板长度的增大能够提高储液器的阻尼比，进而也更能抑制液体的非线性晃动。表4 给出了不同水平挡板长度下储液器的晃动频率值，从表中可以发现，随挡板长度增加，储液器晃动频率逐渐减小，降低幅度最大值可达28%，这说明，水平挡板较大时，它对储液器晃动频率影响较明显，不能忽略，而利用式(20)进行修正后的晃动频率与数值模拟得到的值较接近，能获得较好的预测效果。