考虑配电网安全性的虚拟电厂博弈优化调度

2022-10-11程叶凡张新燕程育红王亚东

水力发电 2022年7期

程叶凡，张新燕，郑浩，程育红，王腾，王亚东

(1.新疆大学电气工程学院，新疆乌鲁木齐 830047；2. 国网冀北电力有限公司检修分公司，北京 102488；3. 国网陕西省电力公司渭南供电公司，陕西渭南 714000)

0 引言

随着高比例风电并网，其发电不确定性为电网的安全稳定运行带来挑战，虚拟电厂(Virtual Power Plant，以下简称“VPP”)的提出为解决该问题提供了新思路[1-2]。目前，仅考虑VPP收益的调度研究取得了一定的成果[3]，但在电力系统中存在发电侧、用户侧、配电网等多个主体，各主体间有一定的利益关系，博弈论的引入为研究该利益关系提供了新方法[4]。文献[5]建立了一种含VPP的电力市场博弈模型；文献[6]基于多种博弈类型建立了多VPP博弈调度模型，提高了VPP的经济效益；文献[7]基于stackelberg博弈理论制定了一种能源共享运营机制，建立了考虑VPP运行商和产消者的非合作博弈模型。上述文献对VPP与其他主体关系的研究多以经济利益为主，忽略了对配电网安全运行的影响，可能导致配电网处于不正常运行状态[8]。此外，建立VPP时选择单一储能存在一定的局限性。针对上述问题，本文采用抽水蓄能和电化学储能，兼顾VPP经济性和配电网安全性，基于非合作博弈理论建立调度模型，通过循环迭代求解，将所得结果分别与VPP经济调度模型及配电网安全性模型进行对比，验证该模型的可行性和正确性。

1 VPP经济调度模型

本文VPP由风电场(Wind turbine，简称“WT”)、燃气轮机(Gas turbine，简称“GT”)、抽水蓄能电站(Pumped-storage power station，简称“PS”)以及电化学储能电站(Electrochemical energy storage power station，简称“ES”)组成，结合PS与ES的优势满足调度计划。VPP作为受价者和受益方，根据市场电价制定负荷电价，电力市场与VPP、负荷交易时按市场电价执行，VPP与负荷交易时按负荷电价执行。

1.1 目标函数

VPP经济调度模型以一天内VPP净收益最大为目标建立目标函数，其中包括VPP与电力市场和负荷的交易收益、VPP中GT、PS、ES以及需求响应(Demand response，简称“DR”)的运行成本。本文建立在已有PS和ES的前提下，故不考虑储能电站的投资成本。VPP经济调度模型为

(1)

(2)

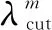
1.2 约束条件

1.2.1 VPP功率平衡约束

gwind(t)+ggas(t)+gdisch1(t)+gdisch2(t)=
G(t)+Gd(t)+R(t)

(3)

R(t)=gchange1(t)+gchange2(t)

(4)

式中，gwind(t)为WT出力；ggas(t)为GT出力；R(t)为剩余电量。

1.2.2 供需平衡约束

VPP与电力市场同时向负荷供电。当负荷电价大于市场电价时，VPP优先向负荷供电；反之，VPP优先向市场供电，此时，电力市场优先向负荷供电。

L(t)-Lcut(t)=Gd(t)+GM(t)

(5)

式中，L(t)为配电网总负荷；Lcut(t)为中断负荷量；GM(t)为负荷从电力市场的购电量。

1.2.3 GT运行约束

(6)

(7)

(8)

-rgas≤ggas(t)-ggas(t-1)≤rgas

(9)

μgas1(t)-μgas1(t-1)≤μgas2(t)

(10)

1.2.4 PS运行约束

(11)

(12)

(13)

(14)

μchange1(t)+μdisch1(t)≤1

(15)

(μchange1(t)+μdisch1(t))-(μchange1(t-1)+
μdisch1(t-1))≤μwater(t)

(16)

1.2.5 ES运行约束

(17)

(18)

(19)

(20)

μchange2(t)+μdisch2(t)≤1

(21)

1.2.6 DR运行约束

(22)

(23)

(24)

1.2.7 购/售电约束

Gmin≤G(t)≤Gmax

(25)

(26)

(27)

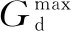
2 配电网安全性模型

2.1 目标函数

配电网安全性模型以一天内配电网各节点电压偏差平方和最小为目标建立目标函数。

(28)

式中，Obj2为一天内配电网各节点电压偏差平方和；N为配电网节点数；Vi(t)为节点i处实际电压；Vref，i为节点i处额定电压。

2.2 约束条件

2.2.1 潮流约束

(29)

(30)

Vimin≤Vi(t)≤Vimax

(31)

θmin≤θij(t)≤θmax

(32)

PMi(t)=GM(t)

(33)

0≤PMi(t)≤PMi，max

(34)

Q(t)=QVPP(t)+QMi(t)

(35)

0≤QVPP(t)≤QVPP，max

(36)

0≤QMi(t)≤QMi，max

(37)

式中，gwind，wi(t)、ggas，gi(t)为节点wi处WT、节点gi处GT有功出力；gchange1，wai(t)、gdisch1，wai(t)为节点wai处PS充放电功率；gchange2，ei(t)、gdisch2，ei(t)为节点ei处ES充放电功率；PMi(t)、QMi(t)为节点Mi处电力市场向负荷提供的有功、无功；Q(t)为配电网无功调节量；QVPP(t)为VPP无功出力；PL，i(t)、QL，i(t)为节点i处有功、无功；Gij、Bij为导纳矩阵实部和虚部；θij(t)为节点i、j之间电压相角差；Lcut，ci(t)为节点ci处中断负荷量；Vimax、Vimin为节点i处实际电压上、下限；θmax、θmin为电压相角差上、下限；PMi，max、QMi，max为节点Mi处电力市场向负荷提供的有功、无功上限；QVPP，max为VPP的无功出力上限。

2.2.2 线路传输约束

Pl，ij(t)=Vi(t)Vj(t)(Gijcosθij(t)+Bijsinθij(t))-
(Vi(t))2Gij

(38)

Pl，ij，min≤Pl，ij(t)≤Pl，ij，max

(39)

式中，Pl，ij(t)为节点i、j之间线路实际传输功率；Pl，ij，max、Pl，ij，min为节点i、j之间线路传输功率上、下限。

3 考虑经济性和安全性的非合作博弈模型

3.1 博弈要素分析

3.1.1 博弈参与者

本文的博弈参与者为VPP经济性指标H和配电网安全性指标P。

3.1.2 博弈策略空间

H的策略空间包括GT出力ggas(t)，PS充放电功率gchange1(t)、gdisch1(t)，ES充放电功率gchange2(t)、gdisch2(t)，中断负荷量Lcut(t)，VPP向负荷的售电量Gd(t)以及VPP与电力市场的交易量G(t)，表示为

(40)

其中，各策略空间应满足式(3)～(27)。

P的空间策略包括各节点的实际电压Vi(t)，配电网无功调节量Q(t)和电力市场向负荷提供的有功量PMi(t)，表示为

SP={SVi，SQ，SPMi}

(41)

其中，各空间策略应满足式(29)～(39)。

3.1.3 收益函数

H的收益为一天内VPP的净收益总值，用IH表示，可通过式(1)求解，净收益总值越高，H的收益越大。P的收益为一天内配电网各节点电压的偏差平方和，用IP表示，可通过式(28)求解，偏差平方和越小，P的收益越大。

3.2 非合作博弈模型

(42)

根据Nash均衡定义可得

(43)

3.3 博弈模型求解

在通用代数建模系统GAMS(General Algebraic Modeling System)中建立考虑经济性和安全性的非合作博弈模型，进行迭代求解，求解流程如图1所示。其中，H和P在各自的策略空间内采用循环迭代进行优化决策，迭代过程如下

(44)

图1 博弈模型求解流程

均衡点初值的选取对求解过程存在一定的影响，若算法不收敛，可以重新选取均衡点初值进行迭代。

4 算例分析

4.1 算例介绍

本文选取某地区域电网作为配电系统进行算例验证，将WT、GT、PS、ES以及电力市场接于节点22、25、11、12、18，系统拓扑结构如图2所示。

图2 改进后的某地区域电网拓扑结构

时段00∶00～06∶00，市场电价为170元/(MW·h)，负荷电价为250元/(MW·h)；时段06∶00～10∶00，市场电价为490元/(MW·h)，负荷电价为500 元/(MW·h)；时段10∶00～15∶00，市场电价为830元/(MW·h)，负荷电价为700元/(MW·h)；时段15∶00～18∶00，市场电价为490元/(MW·h)，负荷电价为500元/(MW·h)；时段18∶00～21∶00，市场电价为830元/(MW·h)，负荷电价为700元/(MW·h)；时段21∶00～24∶00，市场电价为170元/(MW·h)，负荷电价为250元/(MW·h)。

设置调度周期为1 d。GT装机容量为170 MW，最大爬坡率为42 MW/h，固定运行成本为3 250元，启动成本为3 250元。PS储电量上下限为3.5 MW和225 MW，最大充放电功率为60 MW，效率因数为0.85，运行系数为190元/MW。ES储电量上下限为10 MW和90 MW，最大充放电功率为20 MW，效率因数为0.95，运行系数为310元/MW。

4.2 调度计划对比分析

在GAMS中分别对VPP经济调度模型(模型A)、配电网安全性模型(模型B)和非合作博弈模型(模型C)进行求解，得到3种模型的调度计划。

模型A和模型C的调度计划如图3和图4所示。图3为2种模型的VPP各能源出力计划，图4为2种模型的VPP调度计划。

图3 模型A和模型C的VPP各能源出力计划

由图3可知，由于模型A只考虑VPP的经济性指标，且在时段00∶00～07∶00和时段21∶00～24∶00，市场电价低于负荷电价，因此在该时段，VPP优先向负荷供电，并且同时从电力市场购电，将多余的电能存储在PS和ES中，在市场电价高于负荷电价时向市场出售。而在模型C中，不仅要考虑VPP的经济性，还要考虑配电网的安全性，所以在时段05∶00～07∶00和时段21∶00～22∶00，尽管市场电价低于负荷电价，VPP也不再存储电能，通过减小VPP的出力波动提高配电网的安全性。由图3a中时段21∶00～22∶00和图3b中时段04∶00～05∶00、时段22∶00～23∶00可以看出，为执行各模型中VPP的调度计划使得各模型的目标函数达到最优，需要VPP中的储能装置尽力配合，PS由于爬坡率的限制，不能满足VPP 调度计划，此时需要ES的快速反应，配合PS执行VPP的调度计划。对比图3a和图3b可以看出，模型C各能源出力普遍低于模型A各能源出力，并且模型C中燃气轮机出力更加平稳。

图4 模型A和模型C的VPP调度计划

图5 模型B和模型C的调度计划

由图4可知，在模型A中，当负荷电价远低于市场电价时，即时段10∶00～15∶00和时段18∶00～21∶00， VPP不再向负荷售电，只与电力市场进行交易，当负荷电价不低于市场电价时，VPP向负荷大量售电，同时与电力市场进行交易。在模型C中，虽然时段15∶00～16∶00和时段17∶00～18∶00的负荷电价不低于市场电价，但为了使配电网更好的安全运行，VPP依旧未向负荷售电。对比图4a和图4b可以看出，模型C中VPP的交易量及其波动幅度都小于模型A，中断负荷量略高于模型A中的中断负荷量。

模型B和模型C的调度计划对比如图5和图6所示。图5为2种模型的调度计划，图6为2种模型的配电网节点电压。

图6 模型B和模型C的配电网节点电压

图7 模型A、模型B和模型C的调度结果

由图5a、图5b和图5c可以看出，模型B的VPP向负荷的售电量高于模型C，这是因为，模型B只考虑了配电网的安全性，使得VPP尽可能满足配电网的负荷需求，与此同时降低了电力市场向负荷的供电量。在模型B中，任何时刻都是由VPP和电力市场同时向负荷供电，使得一天内各节点电压允许偏差平方和最小。为使得配电网安全性指标达到最优，相较于模型C，模型B中VPP与电力市场的交易量也更加保守。由图5d可以看出，由于模型C需要配电网与VPP通过非合作博弈，使配电网的安全性指标和VPP的经济性指标同时达到最优，即在一天内各节点电压允许偏差平方和最小的同时VPP的净收益最大，所以模型C需要更多的无功调节量来保证配电网的安全性达到最优。对比图6a和图6b可以看出，模型B中配电网的节点电压波动小于模型C中配电网的节点电压波动，并且模型B中的节点电压更趋近于额定电压。