基于模糊神经网络的岩溶发育预测研究

2022-10-11盛建龙俞栋华张彦文

水力发电 2022年7期

盛建龙，乔宇，俞栋华，王平，张彦文

(1.武汉科技大学资源与环境工程学院，湖北武汉 430081；2.湖北省工业建筑集团有限公司，湖北武汉 430076)

0 引言

岩溶(Karst)地质成因复杂、构造特殊，在工程活动中导致了诸多损失。因此，研究岩溶发育，根据发育规律对岩溶发育程度进行评估及预测，可在岩溶环境致灾前做出及时处理，减少岩溶灾害带来的损失，具有重要的工程意义[1-3]。一直以来，很多学者不断进行岩溶相关工程问题评价的探索，如研究岩溶塌陷预测问题时使用了模糊综合评价法[4- 6]，研究岩溶水位与降水量、开采量之间的关系问题时使用了灰色关联度法[7]，研究岩溶隧道突水评估问题时使用层次分析法、区间属性数学法[8]等。对于岩溶发育预测问题，目前有使用层次分析法[9]、模糊评价法[10]等的半经验模型，有使用统计数学方法[11-12]，也有使用层次分析法和贝叶斯网络法相结合的模型[13]。但是，因实际工程问题具有复杂性、不确定性和非线性等特点，在使用传统方法时，过程较繁杂且带有较大的主观性。

神经网络模型能够根据训练样本自动调整结构参数，改变映射关系，具有较强的自适应性，可实现各种非线性映射，较好地解决传统方法中较大的主观性，提高了评估精确性，简化了解决过程。当前，神经网络模型在岩溶相关工程问题中有较多的应用。如BP神经网络被使用在岩溶塌陷预测模型[14-18]，岩溶隧道突水风险预测模型[19]，溶洞规模预测模型[20]等。但对于岩溶发育预测的神经网络模型应用较少。为此，本文结合武汉市某工程区域，建立了模糊神经网络模型预测岩溶发育情况，并与BP神经网络模型做了效果对比。

1 模糊神经网络原理

模糊神经网络(FNN)是模糊理论与神经网络相结合的一种理论。神经网络弥补了模糊系统无法自学习、主观性强的缺点，模糊系统弥补了神经网络对知识提取和表达困难的缺点[21]。模糊神经网络继承了两者的优点，弥补了各自的不足。

模糊神经网络结构见图1。输入层为第1层，此层节点的个数为输入变量的个数，将输入值传递至下一层。模糊化层为第2层，该层实现输入变量的模糊化，即隶属度划分，节点个数为各个输入变量的模糊集合数之和。模糊规则计算层为第3层，该层可细分为求“与”层与求“或”层[21]，其节点分别对应规则Ri的If部分和then部分，通过规则Ri的模糊推理，得到变量的各个模糊集合的隶属度值。输出层为第4层，即反模糊化层，该层将上一层输出的隶属度值进行清晰化，转化为输出变量的精确值。

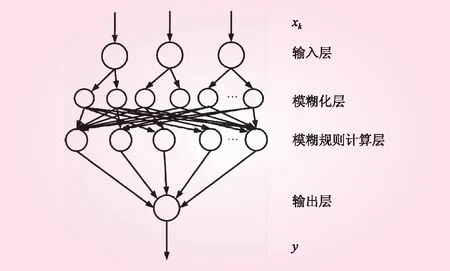
图1 模糊神经网络结构

(1)

(2)

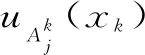
根据模糊计算结果计算模糊模型的输出值，即

(3)

2 模型建立及应用

2.1 相关指标的确定

工程位于湖北省武汉市蔡甸区，总占地面积约32 614 m2，场区西侧毗邻高速公路，东侧距离长江边界约1.2 km，原始地貌单元为长江Ⅱ级阶地湖泊和湖泊滩涂地带，为广袤的填湖区。武汉市软土分布区，无全新活动断层经过，基岩为二叠系泥岩、碳质泥岩及灰岩，下伏灰岩岩溶较为发育，基岩面起伏较大，岩溶裂隙发育。图2为项目场区卫星位置。

图2 项目场区卫星位置(图中标注位置)

拟建场区地下水在勘察深度范围内主要为赋存于上部填土层中的上层滞水和基岩中的基岩裂隙水和可溶岩中的岩溶裂隙水，上层滞水主要由地表水源、大气降水补给，无统一的自由水面，水位及水量随地表水源、大气降水的影响而波动，反映了覆盖层的渗透能力及地表水的影响能力，间接影响岩溶发育。基岩裂隙水主要赋存于各类泥岩中，主要补给来源为地层侧向渗透，水量不大，可不考虑。岩溶裂隙水主要赋存于灰岩的裂隙中，主要补给来源为地层渗透，埋藏深，具承压性。地下水对基岩的潜蚀、冲刷是岩溶发育的主要诱因，结合地下水位、地下水上下波动及基岩标高来考虑，取地下水位高程、基岩标高为评价指标。此外，灰岩作为典型碳酸盐岩，是岩溶发育必不可少的条件，取基岩是否为碳酸盐岩为评价指标。

覆盖层过厚一般会存在多层隔水层或过厚隔水层不利于地下水径流交换侵蚀作用，同时过厚覆盖层形成较大垂向压力，易致岩溶发育所产生土洞塌陷；而覆盖层过薄则易受外界环境因素的影响，取覆盖层厚度为评价指标。

根据勘察剖面图可知，岩层组合可分为单层灰岩、单层泥岩加灰岩、双层泥岩加灰岩3种类型。场区基岩为二叠系泥岩、碳质泥岩及灰岩。基岩分界线北侧基岩为泥岩、碳质泥岩，南侧基岩为灰岩。2种基岩呈不整合接触，接触地带岩石破碎。同时，考虑岩性影响(碳酸盐含量、颗粒大小、与水接触作用面积等)，取基岩层数为评价指标。

表1 训练样本及结果节选

综上，选取地下水位高程(X1)、覆盖层厚度(X2)、基岩标高(X3)、基岩层数(X4)、基岩是否为碳酸盐岩(X5)等5个因子作为输入参数。其中，基岩层数(X4)，单层取1，双层取2，多层取3。基岩是否为碳酸盐岩(X5)，是取1，否取0。输出层对应评价指标，岩溶发育高风险区(勘察到溶洞和土洞)取0.8，中风险区(满足发育条件，但未勘察到明显现象)取0.5，安全区取0.2。输入层个数为5个，隐含层根据2N+1原则取11，输出层为1，因此，网络结构为5-11-1。

2.2 训练及预测

根据地质资料选取数据完整、有代表性的样本81个，其中训练样本69个，测试样本12个。在运算中，模型的模糊隶属度函数中心和宽度均随机赋值，导致每次运行后的结果可能不一样，所以在训练和预测时，采取随机10组的结果求平均值的方法减少样本误差。图3与图4分别是第1组训练样本和节选的4组预测样本的实际输出、预测输出和误差对比。表1为节选的20个训练样本数据。表2为12个测试样本的数据。

图3 第1组训练样本实际输出、预测输出和误差对比

图4 4组测试样本中实际输出、预测输出和误差对比

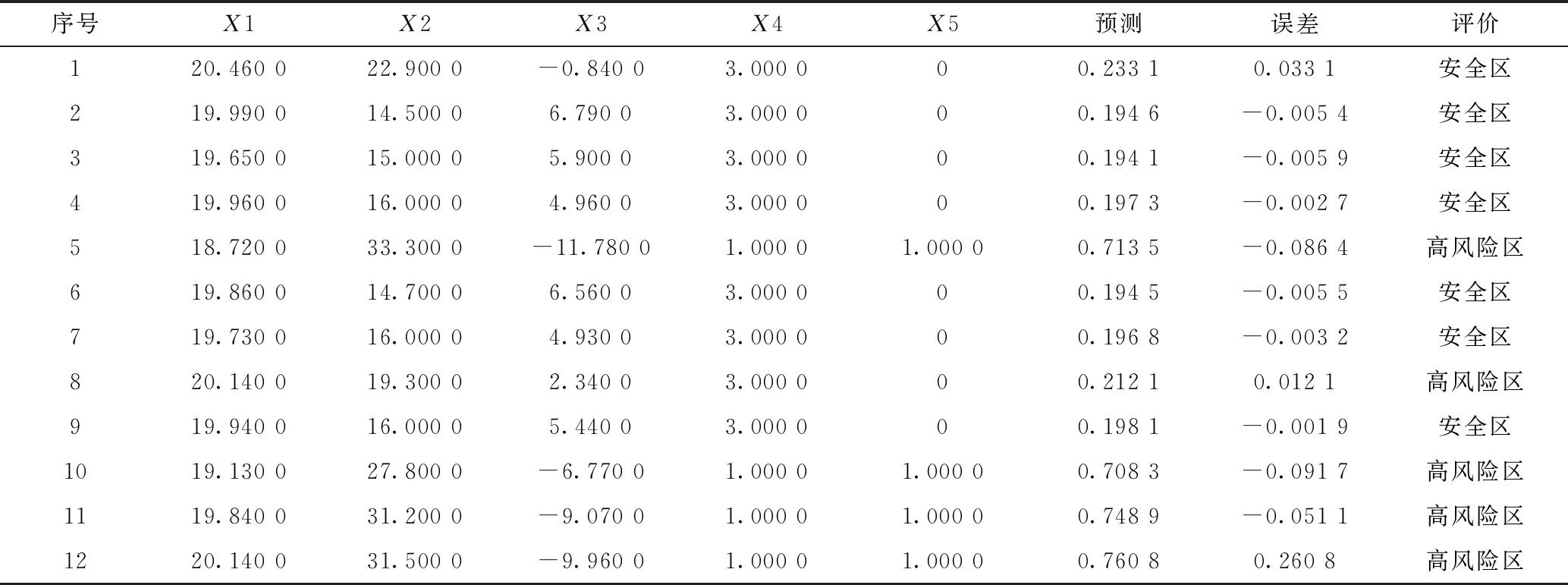
表2 预测结果

图5 4组预测输出与期望输出对比

从图4和表2可知，预测期望值与实际值存在一定的误差，中风险区误差较大。经计算，预测值的平均误差为4.7%，在可接受的范围内，说明该模型可以有效地进行岩溶发育的初步预测。

3 对比BP神经网络模型

3.1 模型对比

预测样本、测试样本与模糊神经网络模型相同，网络结构为5-11-1，学习率为0.01，训练次数为20 000 次，目标精度值为0.000 1，同样采用随机10组的结果求平均值的方法减少样本误差。图5为节选的4组预测输出与期望输出对比。

BP神经网络模型与模糊神经网络模型预测输出数据见表3。从表3可知，在高风险预测中，模糊神经网络模型的相对误差为-9.6%，BP神经网络模型的相对误差为-13.5%，在安全区预测中，两者相对误差分别为1.3%与3.6%。在中风险区预测中，2个模型呈现出较大且相近的误差。与BP模型相比，模糊模型的预测曲线更加接近期望曲线，模糊神经网络模型在高风险区和安全区的预测结果比BP神经网络模型效果更好，精度更高，误差满足工程要求，且2种模型在中风险区预测效果相当。因此，与BP神经网络相比，模糊神经网络模型能够更好地应用于解决岩溶发育初步预测的实际问题中。

3.2 误差分析

支持向量机(SVM)是一个小样本二分类模型，在分析误差原因时，采用“一对多”的方法构建多个SVM模型进行分析。训练结果显示，除高风险与中风险构建的模型准确率较低外，其余的模型准确率都为100%，此结果验证了2种神经网络模型预测结果的可靠性。从2种神经网络模型的输出对比图来看，中风险区的预测输出逼近于高风险区的判断指标，这也与高风险和中风险构建的SVM模型训练结果吻合。因此，中风险区较大误差的外在原因是由于模型将中风险区判断为高风险区。

结合神经网络模型对样本数据的要求，认为其内在原因是由于中风险区样本过少，并采用AUC指数证明此结论。AUC是受试者工作特征曲线(ROC曲线)下与坐标轴围成的面积，可作为一种衡量预测模型优劣的指标，AUC越接近1，模型效果越好。因中风险样本有限，所以用减少高风险样本数量的方式，代替增加中风险样本的效果。将高风险样本数量减少到与中风险相同，建立SVM模型，进行AUC评价。为减少数据带来的误差，随机取10组的评价结果进行平均，表4为AUC评价结果。从表4可知，与初始样本相比，当两类样本数量相同时，模型预测效果显著提升，证实了中风险区较大误差的内在原因是由于其样本过少。综上认为，中风险区较大误差产生的主要原因可能有2点：①工程条件中，中风险区样本数量过少；②工程勘探中，试验孔未能捕捉到岩溶初期发育情况，导致了期望输出指数的确定有偏差。