基于FPGA 的循环汉明码编译码器的设计与实现

李壮壮，刘光祖，孙琳琳，邹骏

（南京理工大学电子工程与光电技术学院，江苏南京 210094）

数字信号在无线信道的传输过程中，受到信道传输特性不理想、干扰等多种因素的影响，码元波形畸变，导致接收端解调判决发生错误，降低了通信系统的可靠性。当通过改变调制方式、发射功率、信道均衡等方式仍无法避免误码发生时，就需要利用差错控制编码ECC（Error Control Coding）来改善通信系统的质量[1-2]。

差错控制编码，又称为信道编码，即信道编码器对传输的信息码元按一定规则加入冗余信息（监督码元）[3]。信道编码主要包括分组码、卷积码等。循环汉明码属于分组码的一种，它不仅能够检测出接收信息码字中的错误码元，还能纠正一位错误码元[4-5]。

一般基于二进制多项式除法器的编码电路需要移位补零，会造成一定的编码延时[6-7]。在译码时，一般的梅吉特译码器搜寻错误图样的时间较长，降低了数据吞吐量。基于上述两点，对编译码器电路进行了改进，成功消除了编码延时并有效降低了译码延时。

1 编译码原理

循环汉明码不仅具有一般分组码的特性，还具有自身的独特性——循环性[8]。循环性指循环汉明码任一码字循环移位后仍为该码中的码字。假设信息位数为k，编码之后的码长为n，监督码元位数为r=n-k。对于r字长的监督码元，组合共有2r种，可以监督的最大码长为2r[9-10]。一个信息码长为n的码字可以表示为如式（1）的多项式（以下mod 均表示模）:

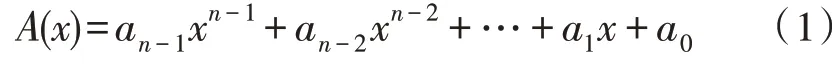
循环移位i次的结果为：

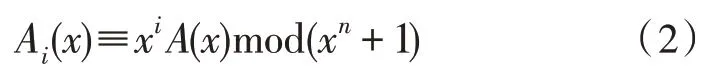
由循环码的性质知，经过式（2）模xn+1 计算得到的码字也为此码中的码字[11]。

一般的循环汉明码编码步骤分为两步：

1）计算并选择生成多项式g(x)。g(x)为xn+1 的因式，且g(x)的最高次幂为n-k[12]。

2）利用g(x) 对信息序列进行编码。假设信息多项式为m(x)，最高次幂为k-1，编码之后的多项式为:

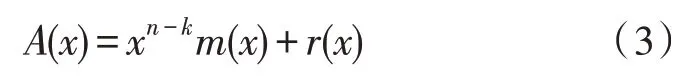
由于所有的码字多项式均可以被g(x)整除，所以A(x)≡0(modg(x))，即：

要使上式成立，需要满足：

因为若xn-km(x)modg(x)≡r(x) 恒成立，二者模2之和必恒为0。

循环汉明码译码方法种类较多，比如最大似然译码法[13-14]、梅吉特译码法[15]等。该次选择了较为实用且相对简单的梅吉特译码法，译码原理如下：

1）计算第n位码元（最高位）发生错误时的伴随式。设发送码字为A(x)，最高位发生错误时的接收码字为:

伴随式为:

即：

2）若第n-1 位发生错误，伴随式为：

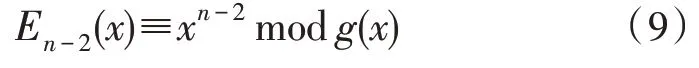
因为:

乘上x即左移一位，确定错误码元位置为次高位。

3）以此类推，若错误发生在第n-i位，伴随式为：

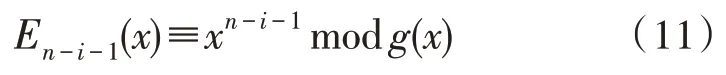
因为:

乘上xi即左移i位，确定错误码元位置为n-i。

2 编译码器设计

2.1 编码器设计

根据上述的编码原理，硬件实现时需要用到多项式除法电路。二进制多项式除法器可以由线性反馈移位寄存器实现。根据式（5），编码器的实现结构如下：

利用图1 结构进行编码时，将所有信息码元输入编码器后还需进行n-k次移位才能得到编码结果。此编码结构有一定缺点，因为需要额外移位n-k次，会产生n-k个时钟延时。在硬件实现时，由于编码延时的存在，若要保证编码后的数据连续送入下一处理模块，需将原始码元缓存，得到监督码元后一并输出。

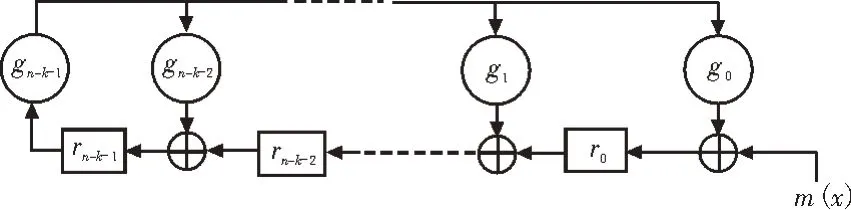
图1 补零编码结构

基于上述缺点，此次采用一种改进的编码方式，消除了上述编码器移位造成的输出延迟。数学原理推导如下：

设被除多项式为B(x)=xn-km(x)，其中：

余式r(x)≡B(x)modg(x)，即：

对于xn-k+1modg(x)有如下关系：

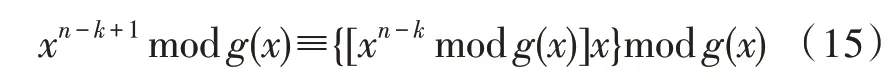
根据式（15）对r(x)表达式进行重写：

①上式中g(x)最高次幂为n-k，B(x)的最低次幂为n-k，将式（17）中ak-1xn-k与g(x)相除，得到最高次幂为n-k-1的余式。

②将①中余式与x相乘，最高次幂变为n-k，然后与ak-2xn-k进行模2 加，并将结果与g(x)相除，得到新的最高次幂为n-k-1的余式，重复上述步骤最后得到的余式系数即为监督码元。

根据式（17），编码器的实现结构如图2 所示。

图2 无延迟编码结构

2.2 译码器设计

梅吉特译码器的译码原理是基于错误图样识别，对于不同的错误图样，伴随式不同，通过识别不同的伴随式确定错误码元位置[16]。

译码步骤如下：

1）使用生成多项式g(x) 整除接收多项式R(x)，求出伴随式r(x)。

2）判断伴随式系数是否全为0，若全为0，无误码，若不全为0，有误码。有误码时，将计算得到的伴随式与本地保存的伴随式进行比对，若两者相同，可确定错误码元位置，若不同，执行步骤3）。

3）对伴随式左移一位，继续除以g(x)求伴随式并与本地伴随式比对，若相同，通过移位的次数确定错误码元位置，若不相同，重复步骤3），直到计算出的伴随式与本地伴随式相同为止。

在上述梅吉特译码方式基础上，额外添加一个检测伴随式，会极大降低译码时间。译码器电路结构主要包含：数据缓冲纠错电路、伴随式计算电路、错误图样识别电路、纠错选择电路。其结构如图3所示。

图3 改进后的译码器结构

为计算添加一个伴随式识别电路对译码时间的影响，设接收码元长度为n，添加的伴随式对应的错误码元位置为：

[·]为向下取整，设(n,k)循环汉明码每次错误一个码元，且不同位置上的码元错误可能性相同，即每个码元错误概率P(x)=，仅采用最高位码元对应的伴随式作为检测目标的平均移位次数为：

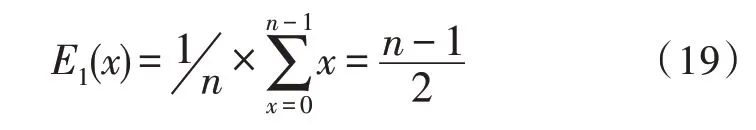
采用上述改进后译码方式的平均移位次数约为：

由上可知，译码延时降低约为一半。

3 编译码器的FPGA实现

此次对循环汉明码（255，247）的截短码（152，144）进行仿真验证，生成多项式选择435（435 为八进制表示，100011101，左侧为多项式最高位）。截短循环汉明码的编译码方式与一般循环汉明码的编译码方式完全相同，唯一的不同在于编译码的有效码元数目不同。

3.1 编码器的实现

编码器结构主要借助图2 编码电路及图4 的状态机得以实现。

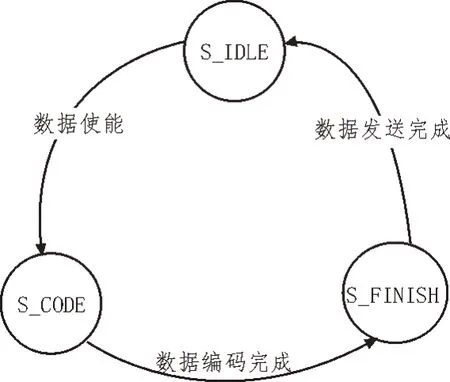
图4 编码器状态转移图

S_IDLE:完成编码前的准备工作，包括将余式寄存器及编码计数器清零、检测数据有效标志的边沿等操作。

S_CODE:完成数据码元的编码。

S_FINISH:完成监督码元输出。在编码完成之后，将监督位依次输出。

3.2 译码器的实现

译码器主要借助图3 中译码电路和图5 译码流程图得以实现。

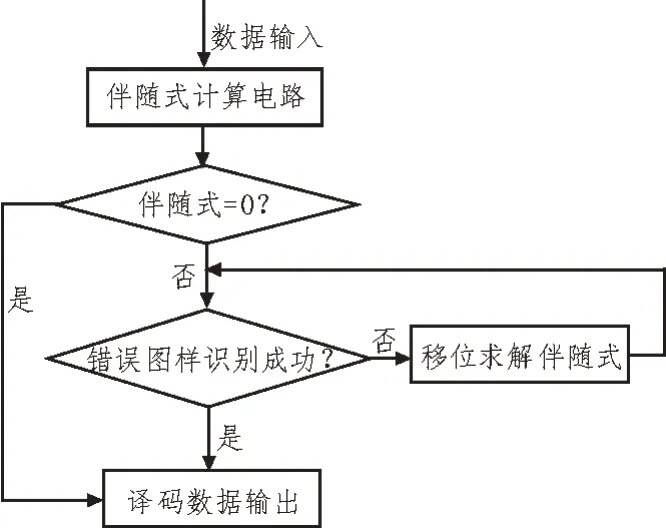
图5 译码器实现流程图

伴随式计算：完成接收多项式与生成多项式的相除，求解伴随式。

伴随式判断：若计算求得的伴随式系数全为0，数据无误码，可将去除监督码元后的数据输出。若伴随式系数不全为0，表明数据有误码。

错误图样识别：完成定位错误码元位置。将本地伴随式与当前计算出的伴随式比对，若两者一致，误码位置即可定位，若不一致，继续将伴随式移位与g(x)相除求解新的伴随式。

编码器电路综合后原理图、资源图分别如图6和图7 所示，其占用资源如表1 所示。

图6 编码器综合后原理图

图7 编码器综合后资源

表1 编码器占用资源

改进前后译码器资源利用图分别如图8 和图9（由于译码器原理图过于复杂，未列出）。

图8 改进前译码器综合后资源

图9 改进后译码器综合后资源

图8 对应只有一个错误图样的译码资源利用率，图9 中对应有两个错误图样的译码资源利用率。综合两图，改进后译码器的资源使用与改进前的相比，LUTs 增加了83 个，寄存器增加了一个。表2中为译码器改进前后占用资源数量

表2 译码器占用资源

4 编译码的仿真结果

图10-13 为两组不同数据的编译码仿真图。此次仿真，时钟频率为80 MHz，周期为12.5 ns。对于编译码器1，编码过程（第一个数据码元开始进入到最后一个码元输出）消耗时钟数目为153（码元输出占用152，外加一个时钟的数据延迟）。可知改进后的编码器相较于一般补零编码器，已经消除了补零带来的延迟。

图10 编码器仿真1

为了验证增加一个检测伴随式带来的优势，实验中两个译码器中错误码字位置有所不同（最低位为0，最高位为151）。对于改进的译码器，该文设置了两个检测伴随式，一个对应最高位（151），一个对应中间位（76）。译码器仿真1 中码元错误位置设置为120，译码器仿真2 中码元错误位置设置为17。译码器仿真图中依次从下向上，1-4 行对应两个检测伴随式的译码器输出，5-8 行对应一个检测伴随式的译码器输出。

观察图11 可知，改进后与改进前译码器错误位置指示变量i最终都定位在32，错误位置为120(152-32=120)。对于改进后的译码器，若错误位置落在151～77 之间，译码时间未改变。观察图13，改进后的译码器的位置指示变量i为60，错误位置为17(77-60=17)，而改进前的译码器位置指示变量为135，错误位置为17(152-135=17)，但对比二者的译码时间，改进后译码器比改进前译码时间减少937.5 ns[理论值(135-60)×12.5=937.5 ns]。

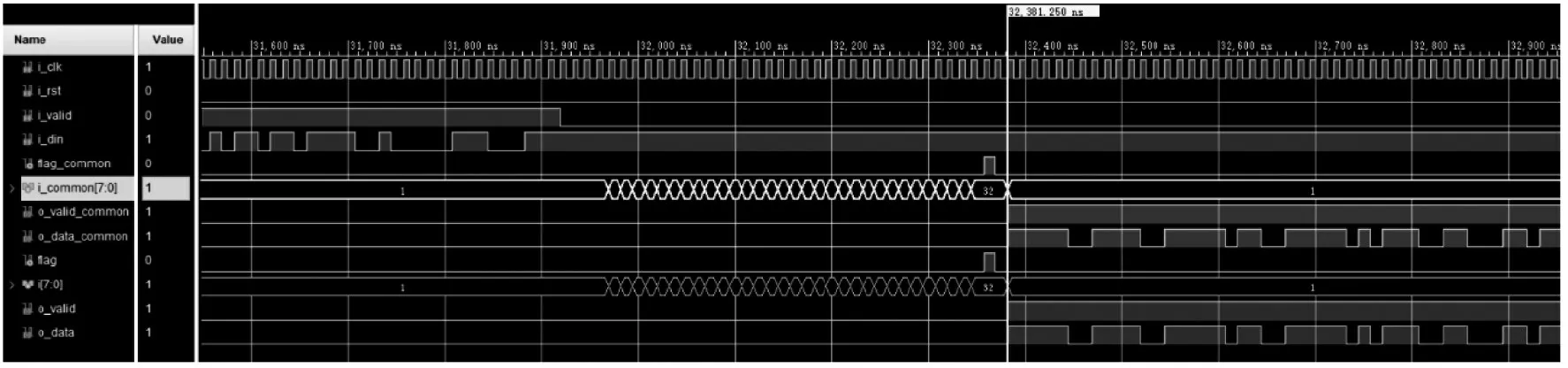
图11 译码器仿真1

图12 编码器仿真2

图13 译码器仿真2

以此类推，也可以尝试加入更多的检测伴随式，将译码的时间缩小更多，该文篇幅有限，不再赘述。

5 结束语

使用Verilog HDL 硬件描述语言对（152，144）截短循环汉明码编译码器进行了仿真，验证了一种无延迟编码方式，并对其数学原理进行了推导。由于在笔者参与的某卫星通信项目中对循环汉明码译码时间要求较高，所以对梅吉特译码器做出了一定改进，通过增加检测伴随式有效降低了译码延时，硬件资源增加较少，满足了项目对译码时间及资源利用率的要求。同时验证了改进后编译码器的正确性和可靠性，具有很高的使用价值和指导意义。