LLC 变换器谐振腔参数设计方法比较

梁康，潘永雄，李键文，徐家锐

（广东工业大学物理与光电工程学院，广东广州 510000）

LLC 谐振变换器的谐振电路工作过程比较复杂，基波近似分析法由于计算简便、满足工程设计要求，被电源设计者广泛使用。在工程应用中，设计者主要采用谐振网络阻抗近似法[1-4]、查图法[5-6]计算谐振腔参数。

基波近似法原本就存在误差[7]，通过查阅电压增益曲线图获取的品质因数Q值存在随机性和不确定性。谐振网络阻抗近似法从谐振网络感容性分界线入手，最终将求出的品质因数Qmax按系数折算后得到符合要求的为了获取精确的Q值并得到最优、简洁的谐振参数设计方法，文中在FHA 的基础上，提出了一种解高次方程法，用于计算谐振腔参数。文中首先介绍谐振网络阻抗近似法和解高次方程法的原理，并对比两种方法所设计的参数，接着通过Saber 软件初步验证谐振参数设计的合理性，再制作实验样机比较其工作状态、效率、精度等，最终确定解高次方程法为最优的谐振参数设计方法。

1 谐振参数设计

半桥LLC 谐振变换器由方波发生器、谐振网络、整流滤波输出三部分组成。

基波近似法假设只有一次谐波分量从谐振腔传递到输出侧，高次谐波分量被过滤掉，不参与能量传递[8-9]。由基波近似法得到的半桥LLC 谐振变换器等效电路如图1 所示。

图1 半桥LLC谐振变换器等效电路

半桥LLC 谐振变换器通过50%的占空比交替驱动开关管通断，进而产生方波电压。因此，谐振网络输入电压的基波分量可表示为：

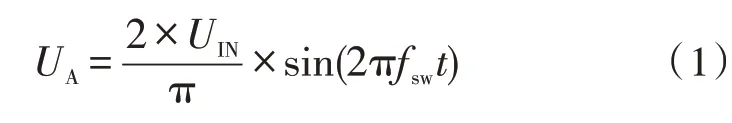
令输出电压为Uo，经过傅里叶变换并折算到谐振网络输出端的基波分量为：

其中，fsw为开关频率，φr为相位角。

若变压器的匝比n=NP/NS，则折算到初级侧的等效交流电阻为：

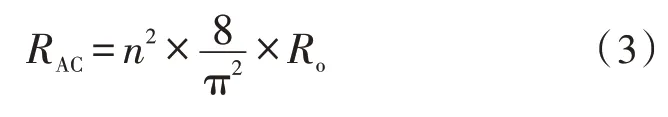
1.1 解高次方程法设计策略

半桥LLC 谐振变换器的电压增益定义为谐振网络输出电压uB与输入电压uA的比值[10]，即：

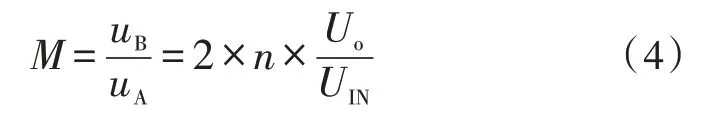
对于磁集成变压器，考虑变压器次级漏感对初级绕组的影响[5,11]，将LLC 谐振变换器的开关频率fsw与其串联谐振频率fr的比值作为归一化频率X，则电压增益简化为：

当变压器匝比和电感比确定时，由于负载越重，Q值越大，变换器最大增益越小，所以在LLC 谐振变换器设计中，应确保最大电压增益满足最大负载需求[12]。因此，可将最小输入电压UINmin所对应的电压增益作为满载下的最大电压增益Mmax。为了防止输入电压降低或者负载突然增加导致电压增益越过峰值电压增益MPK进入ZCS 区域，峰值增益MPK一般取最小电压UINmin对应的最大增益Mmax的1.1～1.15 倍，如图2（a）所示。

在工程上，电感比m一般取2～7[13-14]。电感比越大，谐振腔的环流越小，效率越高，但是会增大变换器开关频率的变化范围，因此必须折中选取[15-16]。在电感比确定后，将直流电压增益通过极值法dM/dX=0，求出峰值电压增益，即：

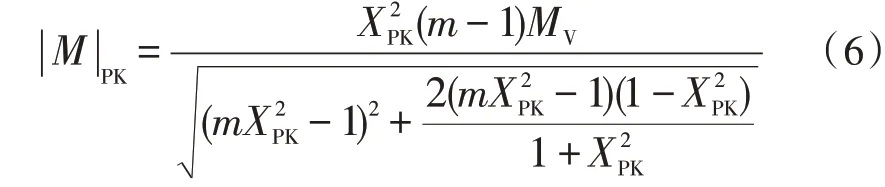
由此可得，谐振电容为Cr=1/2πfrRACQ，谐振电感为Lr=QRAC/2πfr。

1.2 谐振网络输入阻抗法设计策略

由图1可知，LLC谐振网络等效输入阻抗可写成:

进一步化简并令其阻抗的虚部为0 可得：

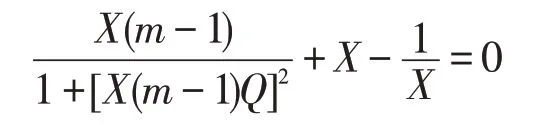
整理可得：

其中，X0为LLC 归一化网络谐振频率。

再将X0和Q代入式（5），得到：

在电感比m确定时，当谐振网络中的Lr、Lm和Cr（等效电阻RAC开路）发生并联谐振时，谐振点的频率就是归一化网络谐振频率X0，这时根据谐振网络输入阻抗近似法，将X0对应的电压增益MX0近似为最大电压增益Mmax。为了实现谐振变换器开关管的ZVS，谐振网络阻抗必须呈现感性[17]，所以要确保归一化开关频率X大于归一化网络谐振频率X0，即归一化网络谐振频率X0可近似于最小归一化频率Xmin。一旦最小归一化频率确定后，由增益曲线可知，负载越大，Q值越大，谐振网络越容易进入容性区域。为确保最大负载都能工作在感性区域，将式（9）所求得的Q值缩小到原来的0.9～0.95，保留充足的余量[18]，如图2（b）所示，最后再求出所需谐振电感和电容。

图2 两种设计方法的ZVS1区域的电压增益曲线

2 实验设计及结果

为了检验解高次方程法和谐振网络输入阻抗近似法设计的谐振参数的差异性，首先根据理论分别计算出120 W、240 W和360 W三种不同输出功率工作在ZVS1区域和ZVS2区域的谐振腔参数。其中，120 W半桥LLC谐振变换器指标为：直流输入电压范围为340～400 V，额定直流输入电压为370 V，串联谐振频率为70 kHz。两种不同设计方法的120 W谐振参数计算结果如表1所示。从表1可以看出，在相同电感比下，与网络阻抗近似法相比，解高次方程法的开关频率变化范围小，品质因数小，谐振电感小，初次级匝数少，而最小开关频率高，谐振电容大。

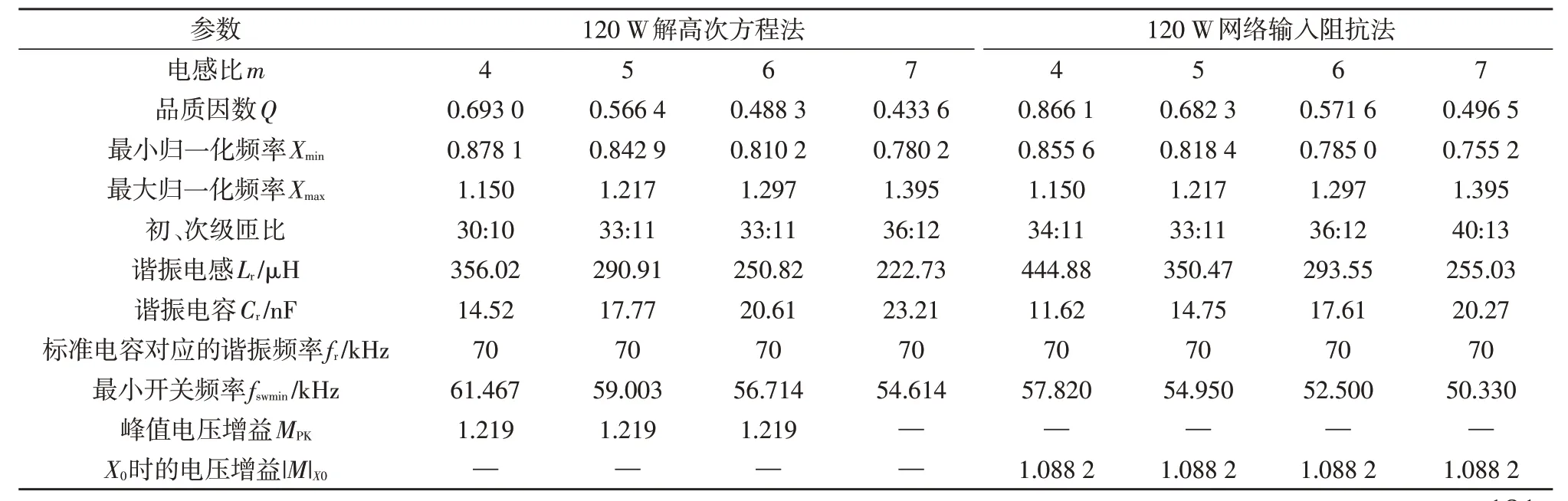
表1 120 W两种方法计算结果

2.1 仿真实验

对比表1 两种方法的数据，选取电感比m为5、初次级匝数相同的参数，在Saber 仿真软件中搭建LLC 谐振变换器，验证设计参数的合理性，其中次级采用全波整流输出，使用肖特基二极管作为整流二极管。该LLC 变换器输出电压为60 V，满载电流为2 A(即输出功率为120 W)，直流输入电压范围为340～400 V，额定直流输入电压为370 V，340～370 V工作在ZVS1 区，370～400 V 工作在ZVS2 区，370 V 对应的频率为串联谐振频率70 kHz，独立变压器骨架为PQ3230(磁芯有效截面积Ae为161 mm2)，独立电感骨架为PQ2020(磁芯有效截面积Ae为62 mm2)。两种方法所得的实际参数分别如表2 和表3 所示。由于受到标准电容的制约，品质因数和谐振电感的实际值比理论计算值偏小。

表2 120 W网络输入阻抗法的实际谐振参数

表3 120 W解高次方程法的实际谐振参数

两种方法的仿真结果分别如图3 和图4 所示，图中的横坐标为时间轴t。图中p 为变换器输出电压，Ir为串联谐振电感电流，Im为变压器激磁电流。在直流340 V 输入时，两种设计方法的仿真结果分别如图3（a）和图4（a）所示。两种方法设计的LLC 变换器都工作在ZVS1区域，可以实现原边开关管的零电压开通（ZVS），次级整流二极管的零电流关断（ZCS）。解高次方程法的最小开关频率为60.596 kHz,与计算值偏差2.7%，网络阻抗近似法与计算值偏差10.86%。由图3（b）和图4（b）可知，在额定电压370 V 下，两种方法设计的变换器在满载时，谐振电流为正弦波，说明其已经工作在串联谐振点上，比较接近理论计算的串联谐振频率70 kHz。图3（c）和图4（c）表明，两种方法都进入了ZVS2 区域，因此，仿真验证了所提方法设计参数的可行性。

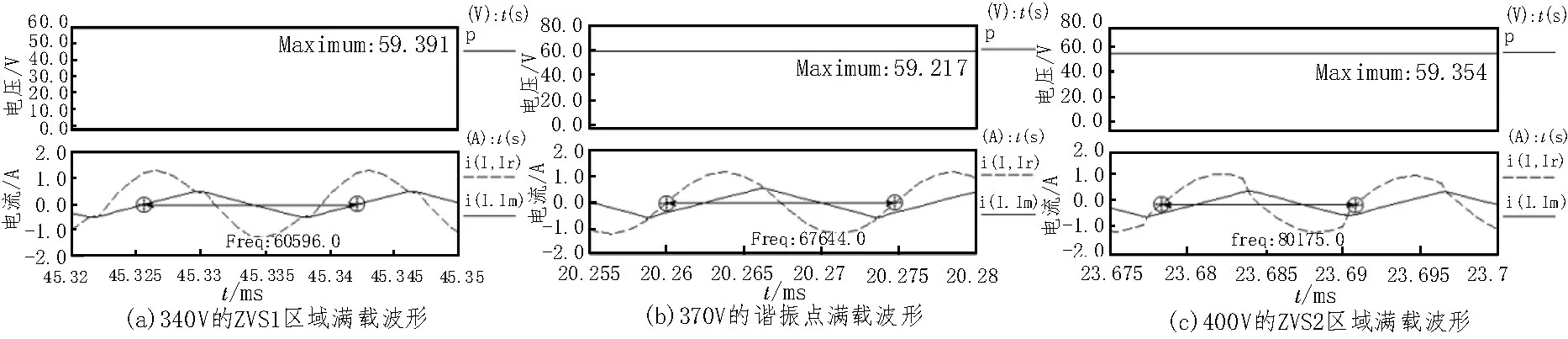
图3 解高次方程法的三种直流输入电压仿真满载波形

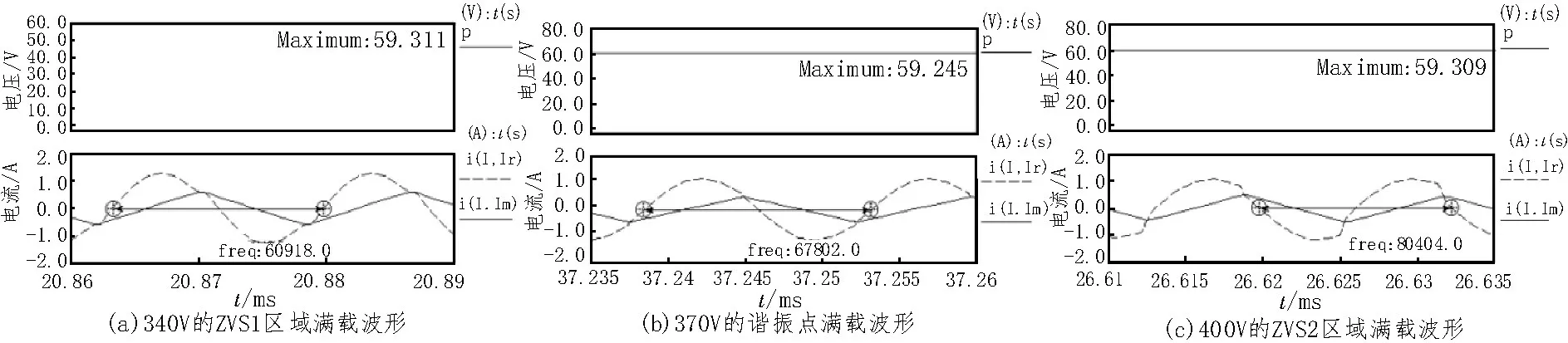
图4 网络阻抗近似法的三种直流输入电压仿真满载波形

2.2 实物验证

为了进一步验证实验的准确性，分析比较两种设计方法的差异性，使用与仿真相同的参数制作了一台半桥LLC 谐振变换器实验样机，并在同一块PCB 板上测试，可相对严谨地比较两者的效率。

在直流340 V、370 V、400 V 输入时，两种设计方法在整机满功率下的下开关管电压Vds、驱动电压Vgs和串联谐振电感电流iLr的不同运行状态波形对比图分别如图5（a）和6（a）、图5（b）和6（b）、图5（c）和6（c）所示。实验结果表明：1）两种设计方法的串联谐振电感电流平台区和开关管的通断临界点相交，说明其都可以实现原边ZVS 和副边ZCS。2）在直流340 V 输入时，解高次方程法设计的变换器的fswmin为60.088 5 kHz，与计算值偏差1.84%，网络阻抗近似法与计算值偏差10.47%。3）两种方法设计的变换器的上下开关管电流波形基本对称，网络阻抗近似法的电流波形相对更加匀称。4）在额定电压370 V输入时，变换器仍然工作在ZVS1区域，解高次方程法的开关频率为70.15 kHz，与理论计算的串联谐振频率偏差0.22%。5）在全电压输入范围内，两种方法样机的开关频率和仿真结果相近，但400 V 时并没有进入ZVS2 区域，而是靠近谐振频率点。由图7 可知，在电感比为5 且匝数相同的条件下，两种方法在不同输入电压下的效率基本一致。增大激磁电感Lm可减小谐振电流，使得效率更优。由表1 可知，网络阻抗近似法的匝数偏多。因此，从侧面反映解高次方程法效率较优。

图5 解高次方程法的三种直流输入电压的实物满载波形

图6 网络阻抗近似法的三种直流输入电压的实物满载波形

图7 三种直流输入电压的整机效率

3 结论

文中基于FHA 提出了解高次方程法快速获取唯一的Q值，进而得到Cr和Lr等谐振腔参数。通过仿真和制作样机的方式，与网络阻抗近似法进行详细对比。实验结果表明，解高次方程法的测量值更加接近理论计算值，频率变化范围小，初次级匝数比网络阻抗近似法略少，整机效率优，为设计人员快速精确计算谐振腔参数提供了参考。