基于改进QPSO算法的双陷波超宽带天线建模*

刘文进， 许馨水， 南敬昌， 高明明

(辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛 125105)

0 引 言

由于超宽带(ultra-wideband,UWB)系统传输信号的频宽很宽(3.1～10.6 GHz)，覆盖了其他窄带信号频段[1,2]，学者通过在UWB天线的辐射单元上开槽[3,4]等方法引入了陷波功能，来避免窄带信号产生的电磁干扰。然而依靠传统的计算机辅助设计(computer aided design,CAD)辅助软件设计优化UWB天线计算量大、耗时长，因此借助神经网络建立天线行为模型具有重要的研究意义。Elman神经网络作为一种典型的动态递归神经网络[5]，既能实现静态系统的建模，也能实现动态系统的映射并直接反映系统的动态特性，被广泛应用于各个领域。量子粒子群优化(quantum particle swarm optimization，QPSO)算法是孙俊等人[6,7]通过建立量子势阱的粒子群模型提出的一种群智能优化算法，能够有效优化神经网络的参数。为了实现更加快速高效建模，本文基于引入维数搜索策略(search for dimension policies,SD)的QPSO(SDQPSO)算法，建立SDQPSO-IElman神经网络智能模型，并应用到一种双陷波UWB天线中实现精确建模。

1 改进的QPSO算法

1.1 QPSO算法

粒子群优化(particle swarm optimization,PSO)算法是将待优化问题可能产生的K个解表述为N维目标搜索空间中飞行的粒子，每个粒子根据其他粒子和自身飞行经验动态调整飞行状态，不断靠近种群中当前位置最优的粒子,并通过轨道模型[8]的形式实现收敛，在此过程中粒子的最大速度会限制每次的运动面积，不能保证粒子的运动范围覆盖整个可行空间。QPSO算法是一种基于PSO算法框架的随机并行概率搜索算法,受量子计算原理中的概率优化算法的启发，认为粒子具有量子行为，粒子在量子化的吸引势场中，受引力的作用产生束缚态，形成种群聚集性，使每个粒子收敛到它的吸引点

pi=[pi,1,pi,2,…,pi,N],i=1,2,…,K

(1)

第i个粒子的位置为

Xi(T)=[Xi,1(T),Xi,2(T),…,Xi,N(T)],

i=1,2,…,K

(2)

种群中粒子能够搜索到的个体最优位置为

Pi(T)=[Pi,1(T),Pi,2(T),…,Pi,N(T)],

i=1,2,…,K

(3)

群体的全局最好位置为

G(T)=[G1(T),G2(T),…,GN(T)]

(4)

在T时刻势阱中第i个粒子的中心位置坐标为

pi=φ×Pi(T)+(1-φ)×Gs(T),s=1,2,…,N

(5)

产生的束缚态确保运动中的粒子在整个可行解空间中进行搜索，由波函数ψ模的平方来确定粒子在空间中出现的概率，利用Schrödinger方程求解得到势阱中每一个粒子的束缚态函数

(6)

利用Monte Carlo算法求得第i个粒子在势阱中T+1时刻的位置

(7)

势阱的特征长度表达式为

Li(T)=2α|C(T)-Xi(T)|

(8)

为了更好控制Li(T)使其收敛，选择在算法中引入平均最好位置变量方法，即

(9)

将式(8)代入式(7)中，则得到QPSO算法的进化方程

Xi(T+1)=pi(T)±α×|C(T)-Xi(T)|×

(10)

以上式子中，ψ与hi(T)均为平均分布在(0,1)区间的随机数。收缩—扩张系数α为算法中唯一需要人为设定的参数，其计算公式为

(11)

式中 MAXITER为最大迭代次数。当α取值较大时，粒子的收敛速度较快，当α取值较小时，粒子的收敛速度较慢，已有数据表明[9]，只有α满足小于1.782时，才能保证粒子充分收敛。

1.2 基于维数搜索策略的QPSO算法

对于QPSO算法，粒子的每个维度通常是随机初始化的，很难保证初始解的大部分维数根据求值函数是最优的，一个具有许多优良维度的粒子可能会因为一些不良维度的影响而被舍弃，从而降低算法的搜索效率。种群中每一个粒子Xi(T)都是N维个体，维数搜索策略将粒子的每一维都视为一个个体，用这个个体替换QPSO中整个粒子，根据评价函数从K-1个粒子中选取每一维度适应度值最好的粒子，组成一个完整的粒子XK(T)。搜索过程如图1。

图1 粒子的维数搜索过程

假设根据评价函数计算出XK-1,1(T)是第一维度中适应度值最好的粒子，则选择XK-1,1(T)作为第K个粒子的一维解，意味着XK-1,1(T)是K-1个粒子中最优维度。按照此搜索方式，继续寻找第K个粒子的下一个维度。通过维数搜索策略，从K-1个粒子中生成包含所有维数的最优解。当得到所有维数时，质点在第T次迭代(T=1,2,…,MAXITER)逐步形成问题的新解XK。在QPSO算法中引入粒子维数搜索策略，既优化粒子的组成，又提高了算法在求解空间中的搜索效率。

2 改进的Elman神经网络

Elman神经网络是一种具反馈功能的动态神经网络，除了输入层、隐含层和输出层以外，在隐含层环节增加承接层作为反馈支路，对隐含层前一时刻的输出进行存储和延迟处理后，同当前时刻的输入数据一起再次作用到隐含层，这种内部反馈机制有利于网络模型的全局稳定性，使Elman神经网络的精度高于BP神经网络，但效果并不明显。为了在使用少量神经元数目的前提下，动态实现高阶系统精度，本文提出在承接层加入自反馈增益因子，并引入直接输入—输出层连接来提高网络的泛化能力。改进的Elman(IElman)神经网络结构如图2。

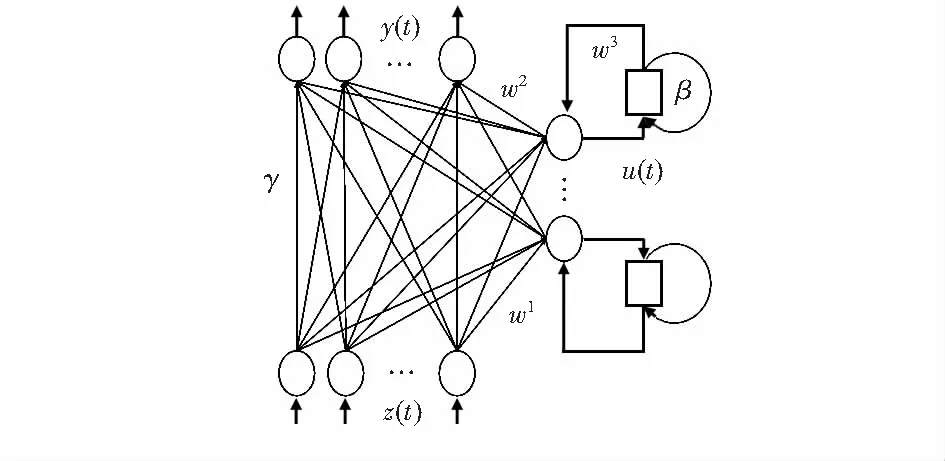
图2 IElman神经网络结构

IElman神经网络的数学表达式如下

y(t)=g(w2x(t)+γz(t))

(12)

x(t)=f(w3u(t)+w1z(t-1))

(13)

u(t)=x(t-1)+βu(t)

(14)

式中w1,w2,w3分别为输入层—隐含层之间，隐含层—输出层之间，承接层—隐含层之间的连接权值；γ为输出与输入之间的连接权值；z(t)为网络的外输入，x(t)为隐含层的输出，u(t)为承接层的输出，y(t)为网络输出。采用Sigmoid型非线性函数作为隐含层神经元的传递函数，用f(*)表示；采用线性函数作为输出层神经元的传递函数，用g(*)表示；t为当前时刻。自反馈因子增益因子β取值为[0,1)，当β取0时，承接层不存在自反馈机制。网络误差函数为E的表达为

(15)

式中e(t)为网络理想输出，M为样本数，j为第j个样本。

3 SDQPSO-IElman模型

为了进一步提高IElman神经网络的精度，采用SDQPSO算法优化神经网络的权值和阈值，具体步骤如下：1)确定神经网络的拓扑结构，初始化网络的权值阈值；2)设置QPSO算法的种群大小K,维数N等参数，初始化K-1个粒子，采用维数搜索策略生成第K个粒子；3)计算当前粒子的适应度值，并与前一时刻的适应度值进行比较，若当前粒子适应度值较好，更新当前粒子的位置为个体最优位置Pi(T)；4)计算种群当前全局最优位置，与前一时刻进行比较，选择较好的更新为粒子全局最优位置Gs(T)；5)根据式(5)更新势阱中每一维粒子的中心位置坐标pi；6)根据式(9)得到种群的平均最好位置C(T)；7)用位置更新公式(10)更新K-1个粒子的位置，采用维数搜索策略生成第K个解；8)重复步骤3～步骤7，直到找到最优解或达到最大迭代次数；9)输出SDQPSO算法得到的最优解，训练神经网络，建立SDQPSO-IElman网络模型。

4 天线仿真与特性分析

本文设计的天线正面与背面基本结构如图3所示，该天线由圆形辐射贴片、介质基板、微带馈线和截短接地板组成。采用FR4作为介质基板，损耗角正切为0.02，高为32 mm，宽为25 mm，厚为1.6 mm。分别在天线的截短接地板和微带馈线上开对称的L形和U形窄缝隙。d5为L形窄缝隙距离介质基板左右两侧的距离，L4为截短接地板的长度。使用HFSS仿真软件对各个窄缝隙的尺寸参数进行优化仿真，得到天线最佳尺寸结构，具体参数如表1。

图3 天线结构

表1 天线尺寸

图4和图5分别为天线的S11和电压驻波比(voltage standing wave radio,VSWR)仿真曲线图，S11的值小于-10 dB，VSWR的值在2以下的波段是UWB天线正常工作的波段。由图可知，中心频率分别在3.5 GHz和7.22 GHz处，实现了双陷波特性，成功滤除全球接入互操作性(WIMAX),卫星X波段和国际电信联盟(ITU)波段三种窄带信号的干扰。

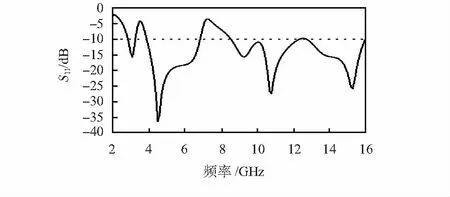
图4 S11曲线

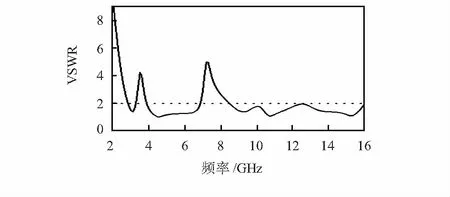
图5 VSWR曲线

5 实验结果与分析

单独使用HFSS仿真软件对天线进行设计往往需要耗费大量的时间[10]和人力，而神经网络具有很强的自适应性，能够学习输入与输出之间的对应关系，从而建立具有天线特性的网络模型。天线的S11和VSWR参数都能够反映天线是否实现良好匹配，这里选择S11参数作为输出，天线的频率作为输入，建立神经网络模型并进行训练。

从HFSS仿真软件中提取500组S11参数和对应的天线频率，训练数据和测试数据分别占80 %和20 %。频率范围为2～16 GHz,步长设置为0.01，为了提高预测精度，先对数据进行归一化处理。利用隐含层节点计算公式确定隐含层的大致范围在2～11，选择不同的隐含层节点数会得到不同的网络误差，经过测试网络误差最小[11]时的隐含层节点数为9，以此确定网络的拓扑结构。分别建立BP，Elman与IElman神经网络模型，用相同的数据对三种网络模型进行训练,在MATLAB 20R2018a仿真平台上进行仿真实验，误差限设为0.001，最大训练次数1 000次。图6为HFSS与三种模型的输出对比，图7为误差对比。由图可知，IElman神经网络模型计算输出更加接近实际输出，泛化能力更强。表2给出3种模型的平均绝对误差(mean absolute error,MAE)分别为：2.610 71,1.357 78,0.576 97，IElman神经网络的误差最小，表明该网络结构模型具有更好的并行信息处理能力，能够很好地描述天线参数间复杂的非线性关系。

图6 IElman等模型输出对比

图7 IElman等模型训练误差对比

表2 不同模型MAE及收敛时间对比

从局部细节来看，IElman神经网络部分计算输出值与实际输出值之间仍存在较大误差，这是因为在训练过程中仍存在易陷入局部极小值的问题，导致个别点无法实现理想拟合，因此,构建SDQPSO-IElman模型来提高模型的精度和收敛速度。种群数量设置为K=30，维数N=28，最大迭代次数MAXITER=100,分别与IElman和QPSO-IElman模型进行对比，结果如图8和图9。可以看出，两种方法均可以改善IElman神经网络模型局部点误差较大的现象，实现良好的预测效果，MAE分别为0.097 86和0.023 79。相较QPSO-IElman网络模型，本文提出的神经网络模型精度提高75.69 %，收敛速度提高8.18 %；与标准Elman神经网络模型相比精度提高98.25 %，收敛速度提高34.81 %。综上所述，本文提出的SDQPSO-IElman模型具有更低的平均绝对误差和更快的收敛速度。

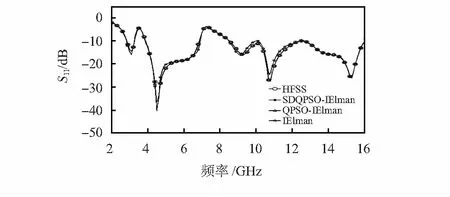
图8 SDQPSO-IElman等模型输出对比

6 结束语

本文在标准的Elman神经网络结构的承接层中增加自反馈增益因子，并引入输入—输出层连接，提高网络泛化能力；利用维数搜索策略筛选出QPSO算法中维数较好的粒子进行重新组合，增强算法寻优能力，使算法收敛速度更快，具有更强的稳态鲁棒性和更高的精度。最后构建SDQPSO-IElman神经网络模型，实现了对双陷波天线的S11参数和频率的精确建模，与其他神经网络模型相比整体性能最优。