地震动作用下刚体扭转效应的振动台模拟试验＊

赵世伟 罗奇峰 潘 康 翟永梅卢文胜 赵 斌 曹文清

1） 中国上海 201254 上海中侨职业技术大学建筑工程学院

2） 中国上海 200092 上海防灾救灾研究所

3） 中国上海 201107 广州市住宅建筑设计研究院有限公司上海分公司

4） 中国上海 200092 同济大学土木工程防灾国家重点实验室

引言

地震动转动分量的研究不仅是抗震理论发展的需要，也是抗震设计的实践需求.大跨度、不规则复杂结构的不断出现，推动了地震动转动分量及其对结构影响的研究（罗奇峰，胡聿贤，1997；Hu，2002；何超等，2011；潘康，罗奇峰，2012）.研究人员通常认为转动现象与转动分量有关，因此可从震后刚体或者结构发生的转动现象入手，研究地震动转动分量，分析结构转动的原因.关于震后刚体翻转的文献资料比较多，例如：1850年西隆大地震发生后，位于印度沙塔克的乔治英格利斯纪念碑发生旋转；1994年日本北海道地震后，一墓碑发生了转动（Kozák，2009），Tobita和 Sawada （2006）对这一转动现象进行了振动台模拟，试验中输入频率为5 Hz的正弦波，得出了模型在接近正弦波峰值的一两个周期内发生转动.然而总体来讲，对转动破坏现象的分析研究尚显不足.2008年汶川地震后，Yang等（2010）在江油考察中发现太白公园曲径桥上的一些石雕发生了不同程度的扭转，本文拟针对该现象进行振动台模拟试验，分析在输入实际记录的地震波时，石雕等效模型的转动破坏现象.

1 曲径桥上石雕的转动现象

2008年5月12日，在我国四川省发生了MS8.0汶川特大地震.在这次地震中四川省江油市太白公园一曲径桥上的石雕发生了转动破坏现象（图1）.从Yang等（2010）一文中可知，该桥共有十八座石雕，其中转动60°，30°和10°的各有一座，转动20°和15°的各有两座，转动5°的有五座，其余六座无转动.

图1 江油市太白公园曲径桥和桥上石雕在汶川地震中的转动破坏现象（Yang et al，2010）Fig.1 Rotation damage phenomena of stone carvings on the labyrinth bridge in Taibai Park of Jiangyou City in Wenchuan earthquake （Yang et al，2010）

2 振动台试验

2.1 模型设计与制作

试验目的是模拟再现汶川地震中曲径桥上的石雕破坏现象，由于石雕形状复杂，试验采用简化等效混凝土模型.各个石雕的位置（角度）相差比较大，其转动效应和平移效应差别也较大.文中共设计建造四类非对称模拟雕塑模型（图2），Ⅱ类模型与太白桥雕塑等效，其设计结构图见图3.等效模型分上下两部分，上部为非对称结构.这类模型有五座，在振动台上的分布及编号（编号 1，4，6，7，8）见图4a，布置这组模型的目的在于考察地震动输入角度对模型扭转角度的影响.其中，模型1的上部结构直接置于振动台面，未作任何粘结.图2中其它三种类型模型的差异在于其非对称性不同，其偏心率相对较小，但Ⅲ类模型的上部结构比较重，它们在振动台上的布置见图4a，编号分别为5，2和3.图4a中各模型俯视图中的涂黑部分为各个模型上部的非对称部分.

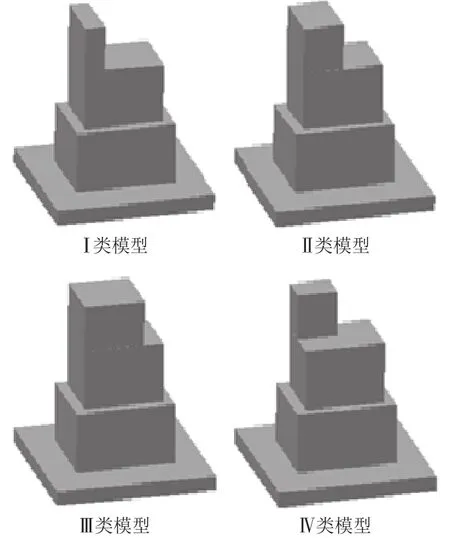
图2 四类模型示意图Fig.2 Sketch maps of four type models

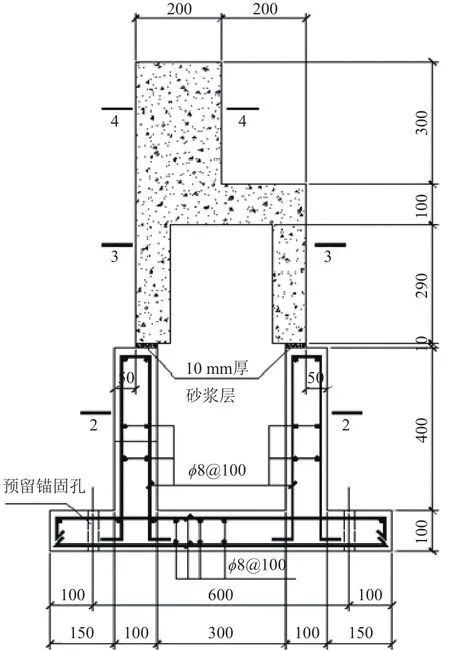
图3 典型模型设计图（单位：mm）Fig.3 Classic model structural map （Unit：mm）

取图4a中模型2和3的连线方向为振动台的x方向，模型1和8的连线方向为y方向，模型1，2，3和5的长边与x轴平行，模型4，6，7和8的长边与x轴的夹角分别为 45°，60°，0°和 30°.图3中的模型采用混凝土浇筑.等效模型的上下两部分用10 mm厚的砂浆粘接，再将模型整体用螺栓固定在振动台上.

图4 模型在振动台上的布置和编号（a）及测量仪器的位置（b）Fig.4 Layout and number of models on the shake table （a） and the location of measuring instrument （b）

2.2 输入的地震记录

试验选用的输入地震波为汶川地震时江油台站（距离太白公园南门约2 km）记录的加速度时程.图5为其东西分量、南北分量和竖向分量，其加速度峰值分别为443.97 cm/s2，512.59 cm/s2和 171 cm/s2.时程经过高频滤波处理，滤掉 25 Hz （工程常用的频率在 0.10—25 Hz）以上的频率.

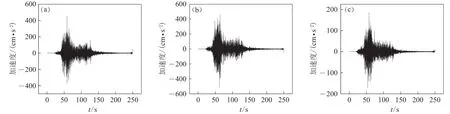
图5 江油地震台东西方向（a）、南北方向（b）和竖向方向（c）的加速度记录Fig.5 Acceleration time histories of EW （a），NS （b） and UD （c） directions for Jiangyou seismic station

2.3 测点布置

试验中采用加速度计和部分位移计间接测量模型中心点处的转动效应.模型1，2，3和5仅布置加速度计，与图4b所示的模型6的位置相同；模型4，7和8布置加速度计和位移计，测点布置与图4b中模型6相同.

2.4 加载工况

试验加载工程如表1所示.x，y和z向分别输入东西、南北和竖向分量.实际地震记录的峰值较大，为了保证试验顺利进行，采用分级加载.El-Centro地震波按0.03g，0.05g，0.10g加载，江油台地震波按原记录的0.3倍、0.6倍、0.8倍、1.0倍、1.2倍和1.5倍加载，工况1—6只加载两个水平向地震动，工况7—12同时加载三个方向的地震动时程.

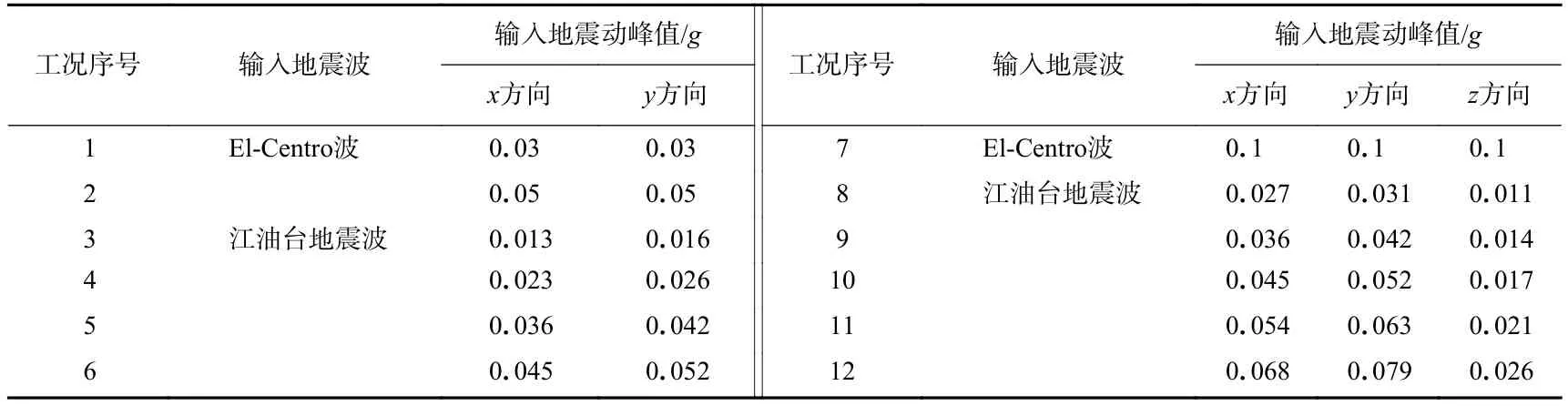
表1 振动台试验加载工况Table 1 Loading working conditions of shake table test

3 试验结果与分析

考虑到此次试验结果记录较多，本文以模型7在工况12的底部左侧（图4b）的加速度时程（x向）和位移时程（x向）为典型记录（图6）.

图6 模型 7 在工况 12 下 x 方向的加速度（a）和位移（b）时程曲线Fig.6 Acceleration （a） and displacement （b） time histories of model 7 in x direction under working condition 12

在工况1—11的加载过程中，除了模型1在工况11下出现转动外，其余模型均未发生转动和错动，仅各模型上下部分的粘结砂浆脱离.加载工况12时，输入地震动时程为原始记录的1.5倍，在输入地震动到原记录的50.8 s左右时，模型开始出现转动现象.表2是试验后各个模型的最终位移和转角（因模型3和5的上部结构无变化，故表中未列出）；图7是模型运动前后的平面图，图中标出的数字为表2各模型对应的位移，为了图示清楚，转角大小未标出.

从图7和8可以看出，模型的转动效应非常明显，从各个模型上取得的位移记录亦能计算出各个模型的转动角度.分别计算模型4，6，7，8在同一高度处的两次位移记录之差，并将其除以这两点之间距离，便可近似得到模型上部非对称部分的转角时程.四个模型的转角时程见图9，可以看出，模型4，6，7，8几乎同时达到转动的最大值，最大转角虽与表2和图6，7有所不同，但趋势是一致的，即模型4，6的转角相同，模型7的动角几乎是模型8的两倍.

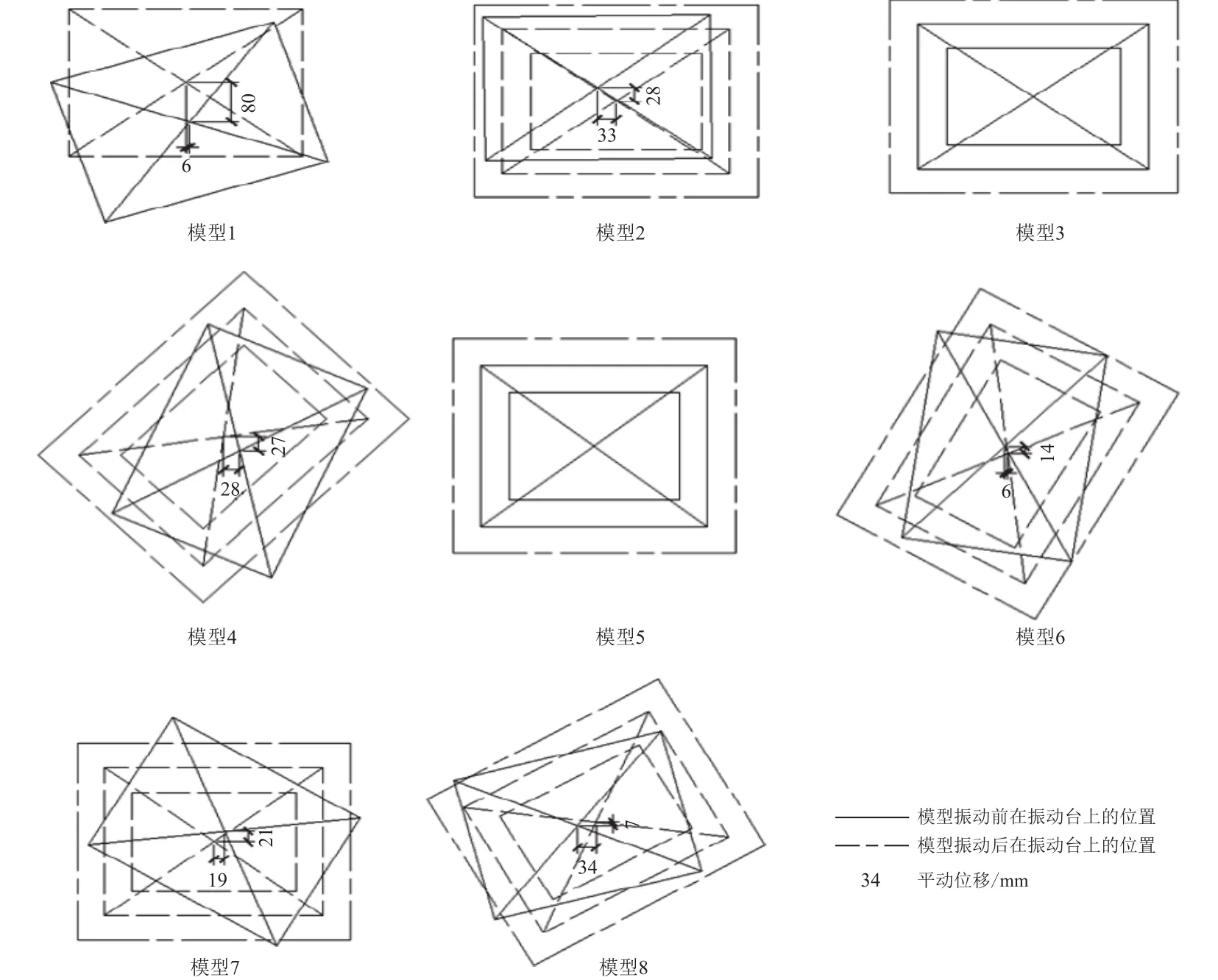
图7 试验后各模型的位移及旋转角度示意图Fig.7 Displacements and rotational angles of each model after test

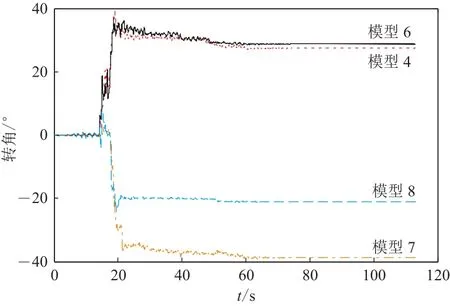
图9 模型 4，6，7 和 8 的转角时程Fig.9 Rotation time history of models 4，6，7 and 8

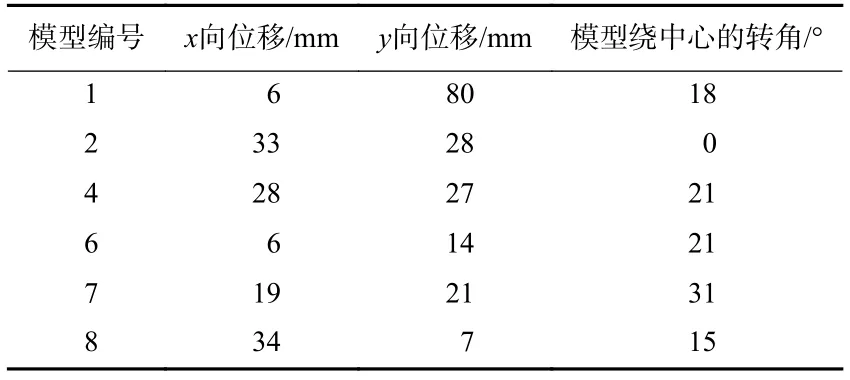
表2 各个模型的位移和转角Table 2 Displacement and rotational angle of each model

试验中，在三维地震动平动分量作用下，模型3和5未转动，模型2发生了平移，其它模型发生了明显的转动.对照太白公园观测到的石雕转动情况（见图1和前文介绍），试验结果与实际观测到的现象较为吻合.

观察试验过程，还可从结构非对称性、地震动输入角度和竖向地震动作用等几方面分析试验结果.

3.1 模型非对称性对试验结果的影响

由图4a可知，模型3和5的偏心率最小且上部结构质量较小，因此未发生转动现象；其它偏心率较大的模型如模型1，4，6，7，8的上部结构在三维地震动平动分量作用下发生了转动.结合刚体运动的相关理论，推断模型发生转动的一个重要原因是石雕的非对称性.试验结果与Yang等（2010）的分析结果一致.模型2虽然偏心率也比较小，但由于其质量比较大，在三维地震动作用下，虽未发生扭转，但沿x和y向分别产生了33 mm和28 mm的位移.

图8 试验后模型在振动台上的损伤状态Fig.8 The damage state of models 4，6，7 and 8 on the shake table

3.2 地震动输入角度对试验结果的影响

各模型在振动台面的布置显示，模型4，6，7，8的长边与x轴的最小夹角分别为45°，60°，0°和30°.从图9不难看出，模型7和8可看作以绕重心逆时针转动为主，而模型4和6则是以绕重心顺时针转动为主.也就是说，与x轴夹角小的以逆时针转动为主，夹角大的以顺时针转动为主.Tobita和Sawada （2006）的试验结果说明结构的响应与输入角度有关，本文介绍的试验也得出同样结论.

3.3 竖向地震动的作用

在工况1—6中，只加载了两个水平向的荷载，所有模型均未发生转动，甚至在台面上放置的模型1的转动也不是很明显，说明双向水平加载虽然会使非对称结构产生扭矩，但此结构仍无法克服上下两部分之间的摩擦阻力.

在工况7—12中，每一工况都有三个方向的加载（两个水平向和一个竖向）.在工况7—10中，所有模型均无明显异动；在工况11的加载过程中，放置在振动台的模型1发生转动，其余模型未见明显变化；在工况12的加载过程中，除偏心率较小的模型3和5未发生位置移动外，模型2以平动为主，其余模型发生了转动.通过分析试验中快速拍摄的照片，可清晰地看到三向加载过程中，模型2的上部结构出现了摇摆现象.这种摇摆减轻了上下两部分的摩擦，导致上下脱开，使模型上部结构出现相对下部结构的移动和摇摆现象.对比两向加载工况下模型的反应，明显地看出竖向地震动起了非常大的作用.过去在分析烟囱和其它建构筑物的转动破坏现象机理时，通常未考虑竖向地震动的作用，本试验说明在此类结构抗震分析中不应忽略竖向地震动对结构地震响应的影响.

图10为试验中模型2发生移动变化的几个时刻，中间的照片说明模型2的上部结构出现摇摆，该片段有助于解释石雕在实际地震中的转动破坏现象.在2008年汶川地震震害调查中发现，多数石雕上的大灯罩掉落，可能也与三向地震动作用下石雕发生摇摆转动有关，由于大幅的摇摆，大型石刻灯罩脱开浅薄的凹凸结合，重心发生偏移，从而自石雕上掉落桥上或水中.

图10 模型2 在三向地震动加载作用下的运动片段Fig.10 The move segments of model 2 under three-direction seismic excitation

4 结论

本文介绍的地震动作用下刚体扭转效应的振动台试验再现了汶川地震中江油太白公园曲径桥上石雕的转动破坏现象，通过试验结果及其初步分析，可以得出以下结论：

1） 在振动台三向加载1.5倍的汶川地震江油台记录的平动加速度，模型的转动情况与实际观测到的江油太白公园曲径桥上石雕的转动情况较一致，说明太白公园曲径桥上石雕的转动破坏现象主要是由非对称结构受三向平动分量作用所致.

2） 当在两个水平方向的地震动输入基础上加入竖向地震动时，模型上部结构的位移轨迹会发生水平平动和摇摆的叠加，使结构出现“颠动”，进而造成非对称上部结构的转动.因此，竖向地震动对结构地震响应的这一影响在抗震设计中不容忽视.

3） 振动台试验结果说明非对称石雕转动方向与地震动的输入角度存在一定关系，但偏心率小且质量轻的上部结构在本文所给试验条件下不容易发生转动和位移，偏心率较小但质量较大的上部结构虽不易发生转动，但会出现两个水平方向的位移.

过去通过振动台模拟转动破坏现象的试验比较少，缺乏这类试验经验，也缺乏测量转动的专门传感设备，对试验中可能发生的情况估计不足，这些都会不同程度影响到试验过程和试验结果的分析.例如未预料到在x和y两个方向施加江油地震台记录的1.2倍时，模型结构仍无反应.出现这一情况后，经分析才考虑三向地震动，增加竖向地震动的输入.从试验结果看，无论两向还是三向地震动输入，工况1—10输入地震动太小，对模型响应影响不大.

本次试验丰富了我们对非对称结构在地震中的转动破坏现象的认识，对其机理的定量分析仍有待深入.