“四含”疏水引起井壁破坏的数值分析
2022-10-10王晓健孙港傲胡显响张飞龙李召胜詹兴泰
王晓健,孙港傲,胡显响,张飞龙,李召胜,詹兴泰
(1.安徽理工大学 土木建筑学院,安徽 淮南 232001;2.淮北矿业(集团)有限责任公司 朱仙庄煤矿,安徽 宿州 234111)
能源是一个国家实现工业化的基石,在国民经济发展中起着核心保障作用,要实现经济可持续发展,必须保证能源供给安全。我国的自然资源具有富煤和贫油的特点,在能源供给上是以煤炭作为第一能源的国家。但是随着近几十年的开采,我国的浅层煤挖掘已经接近尾声,对于深层煤的开采势在必行。深层煤由于地质结构的特点,开挖难度比浅层煤更大,深层煤上部覆盖有松散层,井筒往往需要深入几百米,这意味着井筒需要面临更大的外界压力。井筒的结构和材料容易控制[1],而井筒的受力具有不确定性,因此对井壁进行受力分析以及合理处理显得极为重要。
基于对井壁的负摩擦力分析,目前科研人员主要通过理论分析、物理实验分析、数值模拟分析、工程数据分析等对井筒的受力分布规律进行研究。靳文举等[2]进行了非对称开采对深表土立井井筒稳定影响的数值模拟分析,研究了不同采距情况下井筒各处的位移变化规律;曹广勇等[3]通过探究厚表土薄基岩特殊工程地质条件下的钻井井壁受拉破断机理,使用最小势能原理和弹性力学理论推导出钻井井筒竖向拉应力解析解;姚直书等[4]探究了厚表土薄基岩钻井井筒在突水溃砂情况下的次生竖向受压破坏机理,揭示了发生突水溃砂条件下负摩擦力具有增长迅速和对井筒安全威胁大的特点;郑有雷等[5]对某煤矿井筒破坏与监测信息进行了研究分析,得出在采矿期间地下水位的下降造成了井壁与土层的不同步变形,这种不同步变形对井壁产生的竖向附加力是造成井壁受力和变形增大的主要原因;荣传新等[6]基于薄板弯曲变形理论得出了煤矿立井次生地压与竖向附加力理论解,为疏水沉降过程井壁破裂预测理论的建立提供了一定的参考;孟益平等[7]在冻结复合井壁的工程中运用了有限元方法分析;刘勇等[8]对于多次破裂立井井壁竖直附加力实测及演化特征进行了分析,表明老副井累积的大量附加应变主导的竖向应变,与厚表土层的不断疏水沉降密切相关;吴言霜等[9]通过数值模拟的方法研究了朱仙庄煤矿在疏放水条件下井壁受力变形机理和安全,对井壁内部的应力分布进行了分析;徐辉东等[10]对井壁和土体之间的相互作用提出了塑性剪切力和弹性剪切力的公式,这两种剪切力的解析解不仅可应用于矿山冻结井壁和钻井井壁的竖向力计算,同时还可用于桩的各种竖向力的计算。上述研究分析了各种因素引起土体和井壁发生相对滑动产生负摩擦力的原因和规律,但是上述研究主要集中在疏放水和冻结解冻等所导致的土体变化,未能预测出井壁所受极限沉降量大小以及持续沉降带来的应力变化,并且对负摩擦力的求解没有统一的方法。
鉴于此,文章以朱仙庄煤矿井壁为研究对象,利用数值模拟软件ANSYS接触非线性分析模块,在井壁和土体接触面设立接触对,将“四含”上部土体近似看作一个整体,使用在表土层上部施加不同均布荷载的方法等效“四含”疏水状态,得到井壁在不同沉降量下等效应力的极限值,预测井壁破坏的具体沉降量数值,探究沉降位移和应力大小的关系,将理论分析、数值模拟和现场实况数据进行对比,对井壁受土体沉降产生负摩擦力后井壁内应力分布提供一定的理论依据。
1 工程概况
朱仙庄煤矿目前共有6个井筒,分别为主井、副井、西风井、东风井、南一风井以及南二风井。受地下水疏降影响的主要是主、副井以及西风井。
以副井井筒为计算实例,其井筒最大深度482.8 m,井筒原设计净直径6.5 m,净断面33.18 m2,其中表土段荒径8.7 m,荒断面59.1 m2。淮北矿业集团朱仙庄煤矿为提高回采率,采用“帷幕截流,疏干开采”的方案对“五含”进行疏水处理,由于“五含”和“四含”水力联系紧密,“五含”疏水肯定会引起“四含”水位下降,这将导致地层沉降,对井筒的安全性和稳定性造成严重威胁。为此,本文以朱仙庄煤矿“四含”水位下降引起地层沉降为工程背景,开展疏放水条件下土体沉降对于井壁影响的分析,通过疏水沉降时井壁的受力理论分析、井筒负摩擦力大小及地层沉降的数值模拟和现场井壁监测数据的分析,为煤矿的安全生产提供决策依据,同时也为其他煤矿提供井筒安全性预测的经验。
2 疏水沉降井筒负摩擦力解析解
采用文献[10]中井壁因地层疏水沉降所受竖向负摩擦力的计算公式:
(1)
(2)

3 数值模拟结果和分析
3.1 基于ANSYS接触单元计算原理
ANSYS软件的接触单元类型主要有点-点接触、点-面接触、面-面接触等[11],研究人员通过设立合适的目标面和接触面,输入接触对及接触对的各项参数,就能够完成对接触单元的设置。
ANSYS中具体接触单元的类型是Goodman单元。Goodman等人在1968年提出了一种不具有厚度的四节点岩石节理单元(Goodman单元)用来模拟二维岩体节理之间的相对错动位移,并且在法向方向和剪切方向给出了刚度矩阵的表达式。Goodman单元是一种无厚度以及无质量的单元,和相邻单元只在节点处有力的传递,每个节点具有两个自由度。
3.2 井壁-土体应力场模型和参数
3.2.1 模型建立
根据已有现场井壁和土体的数据,建立物理模型[12]。由于本次模拟着重模拟疏水沉降导致的土体下降产生的负摩擦力,进而使得井壁内部应力重分布,所以选取井壁土体作为研究对象,分析其位移沉降下的应力变化和分布规律。
例如,深层土以0~240 m为例,根据已测得的井壁附近土样数据和井筒结构,视井筒和地层为空间轴对称问题,按照井壁-土体结构建立1/4的三维立体模型,模型长度和宽度等于3倍井筒直径取14.8 m,深度取240 m。模型采用三维8节点固体结构solid185单元,土体采用EDP准则[13]模拟,井壁结构采用弹性本构关系,在井壁和土体接触部分[14],根据实际情况建立接触对,使用targe170和conta174单元模拟井壁-土体接触状态。在井壁处建立目标面,在井壁附近土体处建立接触面。为了使计算更加准确,在井壁处将单元划分得较为密集,在土体部分单元划分较为稀疏,此单元划分方法也能够很好地契合目标面和接触面选取的原则(目标面网格较密,接触面较稀疏)。应力场数值模型共划分了10 560个网格单元和12 904个节点,如图1所示。

图1 静力场数值模型网格划分
3.2.2 边界条件和参数
根据井筒的实际受力状况及附近土体的影响范围,准确反映出井筒和土体的受力状态,确定边界的约束条件。本次模拟在计算模型的左、右、前、后、下为位移约束条件[15],其中前、左边界进行轴对称约束,下边界在z轴方向约束位移为0,后边界施加y轴方向位移约束为0,右方向施加x方向位移约束为0,对整体施加重力荷载9.8 m/s2。土层和井壁计算参数如表1和表2所示。
表1 土层计算参数

表2 C40混凝土参数
3.2.3 模拟步骤
本次数值模拟主要是探究“四含”土体在不同沉降位移下井壁内部应力最大值的变化[16],首先计算出自然状态下土体的沉降量和井壁内部最大应力,其次采用在表土层上部施加均布荷载的方法实现土体的沉降,等效于“四含”土体疏水带来的沉降[17],共进行了11次模拟,分别在表土层顶部施加了0~1 MPa荷载,得到“四含”土体沉降量与自然状态下“四含”土体沉降量的差值,就是“四含”土体在疏水中导致上部土体的沉降量,同时得到受疏水沉降影响井壁内部最大应力值的变化。
4 位移沉降下的井壁应力分析
4.1 数值模拟结果分析
首先模拟的是土体和井壁在原始状态下,井壁的受力状态和变形情况,如图2、图3所示。从图2和图3可知:应力在井壁最深处内边缘达到最大值,其等效应力可达30.9 MPa,在表土层最上部最小;土体的位移沿着深度逐渐减小,在“四含”区域底部压缩量为0.663 79 m。
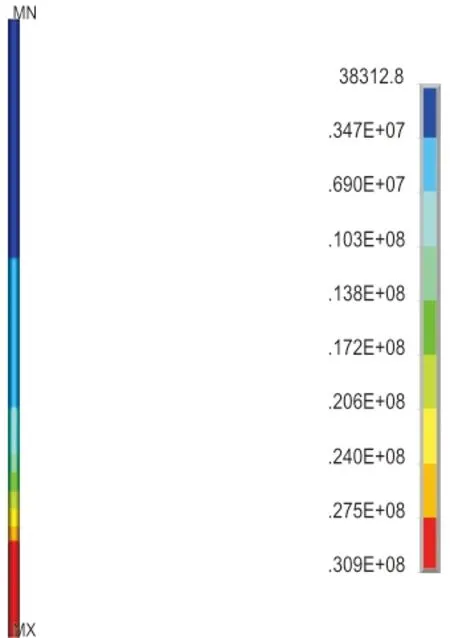
图2 井壁等效应力云图

图3 土体沉降位移
以自然状态下的井壁应力和土体位移为基准点,在顶部施加均布荷载模拟疏水沉降带来的土体固结下沉,随着顶部均布荷载的逐渐加大,具体数据见表3,“四含”土体的压缩量也随之增大,井壁内部最大等效应力也随之增大,内缘等效应力大于井壁外部等效应力,趋势变化如图4所示。当均布荷载加大到0.7 MPa左右时,“四含”相对位移沉降为0.177 228 m,井壁内部应力已经达到C40混凝土的极限承载能力,如果继续加大,井壁将发生破坏。由于数值模拟的过程中没有改变土体和井壁之间的摩擦系数,根据控制变量的原则,可以得出井壁所受竖向摩擦力的增大主要来源于疏水沉降带来的不同深度井壁侧压力的增大,也有可能是井壁接触面附近拉压应力的改变导致井壁内应力增大。
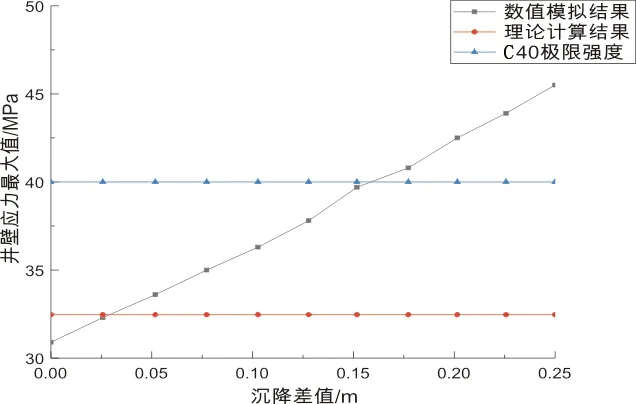
图4 井壁内部应力最大值
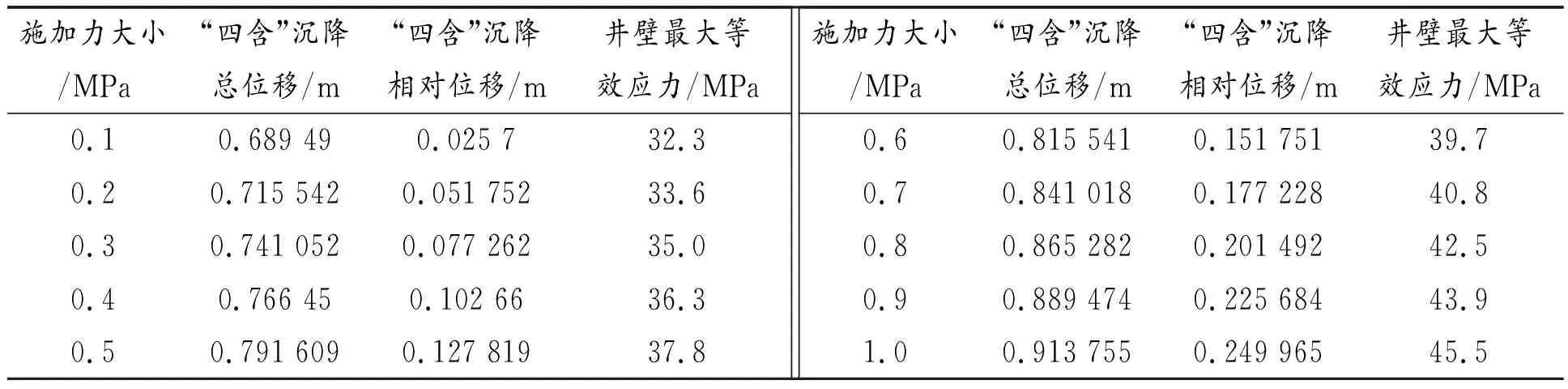
表3 不同沉降位移下应力大小
假设土体发生的是弹性剪切,Ks根据文献[10]取平均值113.86 MPa,井壁外半径3.7 m,内半径2.55 m,Ep=3.25×1010Pa,z为240 m,u0=0.051 75 m,根据公式(1)和(2),可得在负摩擦力的作用下,井壁内的应力大小为32.46 MPa,C40混凝土的极限抗压强度为40 MPa,理论值小于现场混凝土最大抗压强度,井壁处于稳定状态。
由图4可知:当沉降超过0.177 228 m时,井壁将会发生破坏,基于上述分析,结合工程安全、经济性,可优选在井壁处设置一道卸压槽的方案以防止井壁在竖向附加力过大条件下形成破裂[18]。
4.2 现场实测数据分析
为实现对井壁安全性和稳定性的保障,在累深240 m处,使用钢弦式传感器对井壁进行检测,将所测得的频率值处理成应变数据。在井筒投入使用之后,受到复杂地质条件的影响,在初始地压的基础上,内层井壁内缘钢板应变会随着应力发生变化,根据检测的应变数据,可以判断井壁应力值的变化大小。持续检测数据如图5和图6所示。
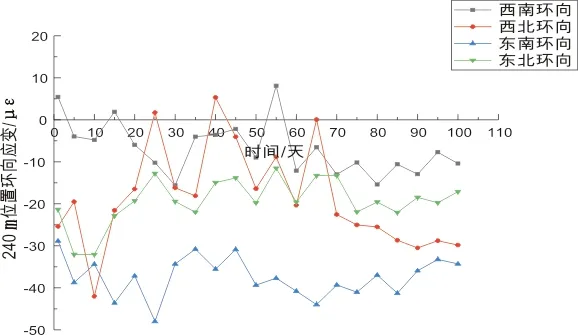
图5 240 m位置环向应变

图6 240 m位置竖向应变

表4 240 m处井壁应变预警值
根据荷载分项系数对井壁应变预警值进行计算,结果见表4,黄色、橙色和红色分别代表考虑荷载分项系数情况下的极限拉压应变。根据图5和图6检测数据可知,环向应变最大为-43.578 8 με,竖向应变最大为-277.116 6 με,钢弦式检测仪器的应变数据处于安全范围之内,趋势逐渐稳定,井壁目前处于安全状态[19]。
5 结论
本次研究的工程背景是修复后的朱仙庄副井井筒,并对内套钢板混凝土井壁受力特征进行分析。修复后的井筒仍处于复杂的工程环境下,作用力复杂,可能导致井壁破坏[20]。本文通过理论分析,数值模拟和现场实时数据检测分析,对“四含”疏水后井壁内部的应力分布进行了分析,并得到以下结论:
(1)在深层井壁的应力分布计算中,理论分析值小于现场实测值,因此需要对理论分析中的u0进行修正,u0在原文献中取值为0.007~0.01 m,假设土体发生弹性剪切状态,u0可取0.04~0.06 m,这一范围符合工程实际。
(2)数值模拟值与现场实测较一致,“四含”疏水导致上部土体沉降,井壁内部所受的应力进一步加大,在沉降达0.177 228 m左右时井壁发生破坏,随着位移的增大,应力也会继续增加,符合工程实际,可以作为预测井壁受力分布的重要方法。通过分析沉降量的增大导致井壁内部应力增大,可能的原因是“四含”疏水导致土体性质的改变,进一步导致井壁与土体摩擦系数变大,另一种可能为“四含”土体被压缩导致井壁侧向压力增大,还可能是沉降带来的井壁与土体之间累加的负摩擦力增加,井壁上缘受到的压力增加,文章未对以上原因进行探究。
(3)通过采用钢弦式检测仪器长时间持续监测,朱仙庄副井井壁目前变形很小,远小于井壁混凝土的拉、压应变极限值,井壁结构安全,因此钢弦式检测仪器可以作为监测井壁变形的重要手段。
