盾构隧道施工引起纵向地表沉降的黏弹性分析

2022-10-10杨召召祝彦知纠永志

河南城建学院学报 2022年4期

杨召召，祝彦知，纠永志

(中原工学院建筑工程学院，河南郑州 450007)

盾构隧道在施工过程中，必然会引起原有土体发生扰动，造成土体应力状态的改变，引起地表结构变形，包括横向变形和纵向地表沉降。横向发生扁平变形，纵向产生沉降，引发隧道衬砌破损、开裂等问题。盾构隧道的施工引起的纵向地表沉降是一个随时间发展逐步趋于稳定的过程。因此要考虑纵向地表沉降的发展随时间变化的关系。目前，盾构法施工引起的地表沉降的计算方法，国内外已开展了大量研究，主要有3种方法。①经验公式法：R.B.Peck等[1]通过对工程资料的分析，提出了沉降分布范围曲线，采用地层损失率估算了地表变形，简化了隧道沉降的计算量。②Mindlin法：Mindlin[2]给出了半无限体的竖向和水平集中力的弹性解；魏纲等[3-4]利用弹性力学Mindlin解，推导了纵向地面变形公式，分析了影响纵向地表沉降的因素，提出了预防沉降的措施；吴昌胜等[5]基于Mindlin解，推导了盾构开挖引起沉降的变形公式，分析了施工参数对地表沉降的影响规律；卢岱岳[6]基于Mindlin解和Loganathan公式对盾构施工的主要因素分别进行数值积分，得出土体弹性位移场。③数值分析法：唐晓武等[7]基于弹性力学Mindlin解，得到了盾构施工引起的总地面变形公式，细化了各个因素的影响范围。但是此方法没有考虑土体黏弹性的特征。侯学渊等[8]利用Peck公式，分析盾构地表沉降数据，提出“负地层损失”概念，提高了Peck公式准确性；柯宅邦等[9]提出了非线性地基模型，采用有限差分法与Newton迭代法，得出隧道在荷载下的纵向变形解析解。以上各种计算和研究方法各有利弊，且试验方法的理论依据大多基于理论解或现有的经验公式，加以推导演化，而且大多数研究都是基于土体为各向同性的弹性半空间体，以此得到的结论丰富了盾构隧道引起纵向地表沉降的理论研究，为研究盾构开挖引起沉降提供了参考。但是很少有文献会考虑土体为黏弹性半无限空间体，导致土体的沉降误差范围较大。

从盾构隧道施工出发，通过分析盾构隧道施工过程中盾构与周围土体之间的相互作用，分析各种因素对于沉降的占比关系，计算结果对实际工程中控制纵向地表沉降具有指导意义。本文采用弹性力学Mindlin解和三参量固体模型相结合的方法，推导了自重应力、正面附加推力、盾构外壳与周围土体的摩擦力引起的地面变形的黏弹性解，研究了盾构施工引起纵向地表沉降的理论计算公式，以期为盾构隧道施工引起的纵向地表沉降提供参考数据。

1 基本理论

材料在一定条件下，同时具有弹性和黏性的特性，综合体现弹性和黏性两种不同机理的形变，这种性质称为黏弹性[10]。材料的黏弹性依赖于时间。时间效应表明，材料的应力应变取决于载荷和变形的过程。黏弹性理论是从宏观唯象的观点讨论材料的黏弹性，表述黏弹性材料的力学性质与本构方程。

三参量固体模型，由一个Kelvin模型和一个弹簧串联而成，如图1所示，该模型能够准确地反映土体的瞬时弹性变形和黏弹性变形。因此本文选择三参量固体模型描述土体的黏弹性本构关系[11]。

图1 三参量固体模型

分别考虑体积应力和体积应变、偏应力与偏应变情形下的黏弹性与效应。三维线黏弹性体微分型本构关系可表示为：

P1sij=Q1eij

(1)

P2σii=Q2εii

(2)

式中：sij为偏应力张量分量；σii为球形应力张量分量；eij为偏应变张量分量；εii为球形应变张量分量。P1、P1、Q1、Q2为微分算子，表达式分别为：

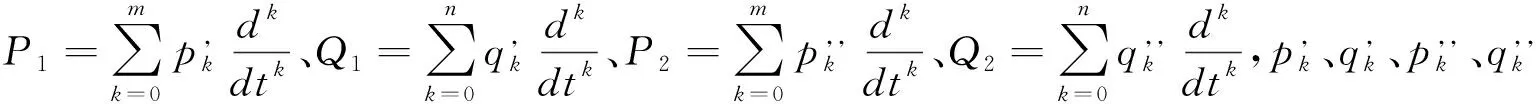
分别对式(1)和式(2)做关于t的拉普拉斯变换：

(3)

(4)

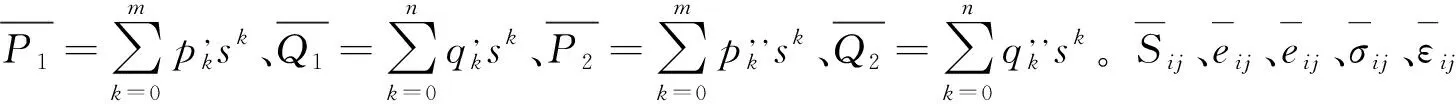
对三参数固体黏弹性模型有：

(5)

(6)

(7)

(8)

式中：K为弹性体积模量，G1、Gk、ηk分别为三参量参数。

对于黏弹性材料来说，可以得出材料剪切模量、黏性模量和土体黏弹性泊松比为：

(9)

(10)

(11)

2 盾构开挖引起土体纵向地表沉降的黏弹性分析

2.1 纵向地表沉降的影响因素分析

盾构隧道施工引起纵向地表沉降的主要因素有3个方面。①正面附加推力。为维持开挖面的稳定，开挖面需要提供一定的支撑力，支撑力通常略大于掌子面静止土压力。盾构机正面推力与静止土压力之差即为正面附加推力。②盾壳与周围土体之间的摩擦力。摩擦力可引起纵向地表沉降。此处可简化为沿盾体表面的均布荷载。③开挖卸载后，由于盾尾施工和注浆等因素造成土体损失，引起纵向地表沉降。

因此，在求解盾构推进引起纵向地表沉降时，必须考虑以上因素的叠加效果。根据以上分析，总的纵向地表沉降分别由正面附加推力、盾壳与周围土体的摩擦及土体损失3个因素综合作用引起。土体损失导致的地表变形不涉及黏弹性参数，因此本文不考虑土体损失产生的纵向地表沉降[12]。

2.2 基本假设

采用黏弹性理论分析计算时，需作如下假设：①土体为连续均质各向同性的黏弹性介质；②土体处于三维应力状态，偏张量与球张量满足三参量固体模型；③限于小变形的情形。

2.3 地表沉降弹性解

2.3.1 地表总沉降的弹性解

以弹性力学半无限体在自重应力作用下的弹性沉降解为基础，以弹性-黏弹性相应原理分析即可得到盾构施工引起沉降的黏弹性解。盾构上方土体表面沉降的弹性解为[12]：

(12)

式中：μ为泊松比；E为弹性模量；P为土体的自重应力；R为盾构半径；ω为沉降系数。

2.3.2 正面附加推力引起的纵向地表沉降计算

正面附加推力引起掌子面前方和后方的沉降相反。在施工时引起的地面变形较小。如图2所示，取微分面积rdrdθ，利用弹性力学Mindlin解，求得隧道上方的纵向地表沉降计算公式为[3]：

图2 力学分析模型图

(13)

2.3.3 盾壳与周围土体的摩擦力引起的纵向地表沉降计算

盾构在施工过程中，盾壳与周围土体之间会产生摩擦力。如图2所示，盾构表面取微分面积Rdrdθ，引起的纵向地表沉降计算公式为[3]：

(14)

2.4 土体表面各个形式变形公式的黏弹性分析

土体总的纵向地表沉降的弹性解为W纵=W2+W3。根据弹性-黏弹性相应原理，对W1、W纵分别作关于时间t的Laplace变换和Laplace逆变换。可得：

(15)

对W纵的各个分式进行Laplace变换和Laplace逆变换得：

(16)

(17)

由式(15)可知，当t=0时，黏弹性蠕变参数Gk=0，初始沉降值为：

(18)

分析知上式与弹性解公式保持一致，可验证黏弹性位移沉降解的准确性。

3 实例分析

为了分析盾构施工引起的地表沉降规律，并验证本文黏弹性计算模型的合理性，采用MATLAB编制程序进行计算。以中铁一局集团有限公司承建南通市城市轨道交通2号线一期工程土建施工06标段项目为实际案例进行分析，南通市地处长江下游冲积平原，地形平坦，地貌类型单一。总体上，本标段拟建地下区间沿线地势一般较为平坦，土层为粉质黏土，灰色，软塑，压缩性中高等，土质基本均匀。具体土质参数为：γ=18.3 kN/m3、K0=0.48、R=3.1 m、P=311 kPa、P1=15 kPa、P2=43 kPa。部分土体参数及黏弹性计算参数见表1、表2。

表1 土体参数

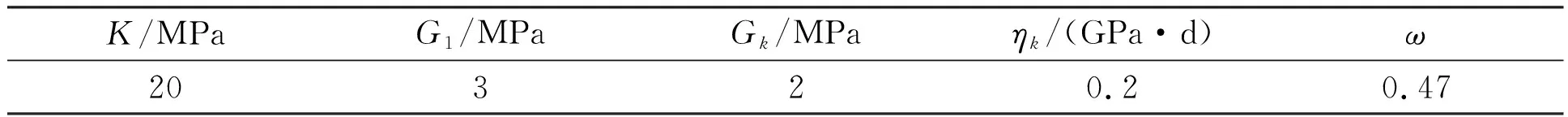
表2 黏弹性参数

3.1 自重应力引起的总沉降

通过计算所得盾构土体上部自重应力引起的总沉降如图3所示。从沉降发展情况来看，可得总的自重应力引起的沉降最大值为38.3 mm，其中初始沉降为27 mm，在考虑黏弹性的基础上，自重应力引起的总沉降为11.3 mm。

图3 盾构推进引起的总沉降随时间发展曲线

3.2 正面附加推力和盾壳与周围土体摩擦力引起的沉降

正面附加推力引起的纵向地表沉降如图4所示。沉降峰值出现在x=±12 m 的位置，在x=±12 m 时纵向地表沉降最大，达到±0.26 mm。沉降变化较大的范围为±40 m，随后曲线斜率变化稍缓，变化逐渐趋于稳定。图5表示在时间和距离的共同作用下，盾壳与周围土体之间的摩擦力作用引起的纵向地表沉降曲线。在掌子面负方向上，x=-16 m 时引起的纵向地表沉降最大，达到3.97 mm，x=-52 m 之后，沉降趋于稳定逐渐恢复至原来的水平。在正方向上，x=8 m时，沉降值最大达到3.97 mm，x=44 m 以后，沉降值趋于稳定逐渐恢复到原来水平。

图4 正面附加推力引起的纵向地表沉降

图5 盾壳与周围土体摩擦力引起的纵向地表沉降

3.3 盾构推进引起的总纵向地表沉降

图6表示在时间和距离的共同作用下，盾构推进作用引起的纵向地表沉降曲线。在掌子面负方向上，x=-16 m 时纵向地表沉降最大，达到4.21 mm，x=-53 m之后，沉降逐渐趋于稳定，x=100 m时，沉降基本恢复至原来水平。在正方向上，x=8 m时沉降值最大达到4.21 mm，在x=46 m以后，沉降值逐渐趋于稳定，在x=100 m时，沉降基本恢复到原来水平。盾构后方沉降在x=2L处达到最大值，盾构前方沉降在x=L处达到最大值。从距离来说，在掌子面±40 m范围，沉降活动范围较大；从时间来说，在推进过后200 d内，沉降达到稳定值。引起的沉降曲线在掌子面处关于原点中心对称，且随着时间发展，由于土体的次固结沉降，沉降量在缓慢增大，不过增大的沉降值微乎其微。

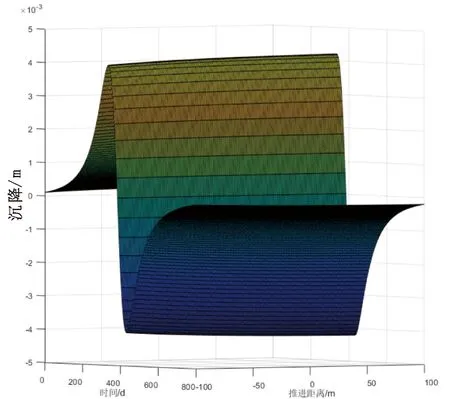
图6 盾构施工引起的纵向地表沉降曲线

图7表示土体在考虑黏弹性基础上，盾构施工引起的纵向地表沉降的各个因素及总体地面沉降对比分析图。纵向地表沉降为4.21 mm，总体沉降为11.3 mm，综合各种引起沉降的因素，可知纵向地表沉降占总沉降的比例约为37%。从总体来看，盾构施工引起的纵向地表沉降曲线表现为前方土体隆起、后方土体沉降。就沉降比例而言，正面附加推力引起的沉降较小，约占总体纵向地表沉降值的1/16。盾壳与周围土体的摩擦力引起的沉降占比较大，约占总体纵向地表沉降值的15/16。盾壳的摩擦力对地面纵向地表沉降的影响要远大于正面附加推力引起的影响。结合上述沉降曲线来看，因为沉降值本身较小，时间跨度较大，黏弹性模型中，时间参数相对沉降来讲不敏感。