人口集聚与碳排放：基于空间溢出效应视角的经验考察

孙 猛，费不凡

（吉林大学 东北亚研究中心，吉林 长春 130012）

一、引言

进入21 世纪以来随着社会主义市场经济的快速发展和城镇化进程的不断加速，中国人口不断向城镇地区流动和迁移，形成了空间分布上的人口集聚形态。第七次全国人口普查数据显示2020年城镇常住人口数量超过9亿，占总人口的比重达到63.9%，中国已经迈入城市型社会阶段。人口集聚意味着劳动、资本以及基础设施等生产要素向城镇地区集中，由此引致的产业集聚、经济集聚势必对能源消耗和温室气体排放产生重要影响。当前中国已经跻身全球第二大经济体，经济规模的进一步扩大也使我国成为化石能源消耗和二氧化碳排放的第一大国，节能减排的压力之巨大显而易见。2020 年中国提出力争于2030 年前碳排放达到峰值、努力争取2060 年前实现碳中和的国家自主贡献目标，并将其写入了国民经济和社会发展的“十四五”规划之中。伴随新型城镇化和城市群经济等区域发展战略的持续推进，“碳达峰碳中和”战略的实施必然要求中国经济在集聚效率与碳排放之间进行权衡和协调。节能减排的目标约束既对中国未来的经济发展提出了重大挑战，同时也为中国经济的绿色转型提供了重要机遇和杠杆。［1］

人口集聚与节能减排作为中国经济实现绿色转型发展的重要推力和目标函数，二者之间可能存在不容忽视的内在联系。人口集聚推动了中国城市化经济和地方化经济的兴起，可能通过生产要素的重置效应而对节能减排的影响表现出双重作用。一方面，人口集聚作为一种紧凑型空间经济形态，能够产生规模经济、知识溢出等正外部性，有利于提高技术创新效率和要素使用效率，进而表现出促进节能减排的积极作用。另一方面，空间上的人口集聚又可能造成生产规模过大和拥挤成本上升等负外部性，加速能源过度消耗并产生额外的碳排放，从而不利于节能减排目标的实现。此外，由于中国地区之间的交流合作愈发频繁，人口集聚和节能减排的空间依赖特征越来越明显，一个地区的碳排放往往受到周边地区要素流动的关联作用影响。因此，如何把握人口集聚、经济发展与碳排放之间的关系以及促进三者协同发展，不仅是当下可持续发展理论研究中的一大热点，同时也是中国经济实现绿色转型发展进程中一个非常值得探究的现实问题。

二、文献综述

人口集聚是指人口向确定区域快速集中所表现出的一种紧凑型空间形态，往往会带动生产要素集中进而对区域经济增长和污染排放产生重要影响。从现有文献的研究结论来看，人口集聚对碳排放的影响通常具有双重效应。一方面，人口集聚带来的经济活动集中会产生集聚效应，能够通过规模经济和技术溢出减少能源消耗和降低碳排放量。Ohlan 使用印度1970-2013年期间的年度调查数据证实了人口密度有利于减少二氧化碳排放，因为人口集聚程度越高的区域经济发展往往越好，在执行环保制度方面具有更为积极的意识，进而实现节能减排。［2］Yu 等人利用2005-2016 年长三角25个城市的面板数据，采用空间STIRPAT 模型研究发现城市人口规模与碳排放强度呈负相关，而且技术进步、人口规模等驱动因素具有空间依赖性和空间溢出效应，这意味着人口集聚的城市群排放效率更高。［3］最近一项研究采用了中国碳核算数据库（CEADs）提供的175个城市排放清单的截面数据，研究结果表明城市人口规模虽然提高了二氧化碳排放总量，但是人口密度的提高却能够带来人均二氧化碳排放的减少。［4］另一方面，人口过度集聚也会产生拥挤效应，造成生产成本和生活成本的上升，进而加剧能源消耗和碳排放。O′Neill 的研究表明城镇化会导致碳排放量快速增加，尤其是在劳动力需求旺盛的发展中国家和地区，［5］陈向阳利用经济增长模型得出了同样的结论并提供了中国的经验证据。［6］周健等人在运用ARDL模型研究中国人口特征、经济增长与碳排放的关系中也发现无论短期还是长期，人口增长都将导致碳排放总量增加。［7］

人口集聚对碳排放的影响取决于上述双重效应的综合结果，由此一些实证研究也揭示了二者之间的非线性关系，在更长的时间跨度内人口集聚对碳排放的影响存在阶段性特征。李卫东和余晶晶利用1995-2010年中国30个省份的数据估计了面板STIRPAT模型，结果表明城镇化对二氧化碳排放的影响呈“倒U”型。［8］Wang 等人通过对2005-2015 年中国166 个城市的空间面板模型测试发现城镇化与碳排放之间存在一条“倒U”型曲线，城市空间集聚能够在一定程度促进拐点的早期到来，从而减少碳排放。［9］最近一项采用城市Kaya关系和简化主轴回归对中国2000-2016年城市排放模式的研究揭示了人口规模与碳排放之间呈“倒U”型关系，大城市的人均排放量往往较低，人口聚集可能有助于减缓气候变化和向可持续性的更广泛过渡。［10］尽管城镇化在一定程度上反映了人口的快速集聚，但是城镇化具有更为广泛的经济内涵，因此这些非线性证据对人口集聚与碳排放之间因果关系的揭示并不充分，这需要采用更为准确的人口集聚指标做进一步的经验测试。何文举等采用中国省份面板数据估计了人口密度集聚效应和拥挤效应的阶段性特征，发现省域范围的人口集聚与碳排放之间呈“N”型曲线关系。［11］柴志贤利用1999-2008年中国30个省会城市的面板数据研究发现人口密度与城市人均碳排放呈“U”型曲线关系。［12］陈飞等利用多项式函数关系及偏最小二乘法综合回归模型，揭示了上海市单位土地面积的人口密度与碳排放之间呈“N”型关系，而且人口密度比建筑和经济密度对碳排放的影响更大。［13］另一项研究利用DMSP/OLS 夜间灯光数据核算出中国地级及以上城市的人均碳排放量，并通过动态面板模型测试揭示了城市人口密度与人均碳排放之间的“U”型曲线关系，而且中国70%左右的城市实际人口密度要低于最优人口密度。［14］

除人口集聚以外，一些实证研究还揭示了经济增长过程中能源结构、能源强度、产业结构、［15］技术进步、［16］发展水平等因素对碳排放的不同影响。［17］朱欢等使用全球67 个经济体1990-2018 年的面板数据，利用联立方程模型证实了碳排放与经济增长之间的环境库茨涅茨曲线。［18］中国各省份的经济发展也同样存在碳排放的“倒U”型变化趋势，［19］最近的一项研究也提供了更为丰富的经验证据。［20］至此不难发现人口集聚和经济发展对碳排放的影响存在类似关系，这是因为人口集聚通过经济活动才能产生集聚效应和拥挤效应。但是现实中的人口集聚往往滞后于经济集聚，［21］因此其必然会借助多种经济渠道对碳排放产生不同的影响，进而决定了二者之间的非线性关系。杨东亮和李朋骜利用工具变量回归方法为人口集聚的经济增长效应提供了经验证据，［22］李晓阳等进一步揭示了人口集聚对经济发展的影响呈“倒U”型关系。［23］此外，人口集聚下降造成的城市收缩会降低能源效率和创新能力，［24］中国城市层面的人口集聚对技术创新、［25］产业结构升级具有显著促进作用。［26］

现有文献针对人口集聚、经济发展与碳排放之间的两两关系展开了较为丰富的探讨，但是少有文献将三者纳入同一分析框架进行深入研究。从逻辑上来看，人口集聚作为一种紧凑型的空间经济形态，所产生的外部性和溢出效应对碳排放具有重要影响，而正是经济活动方式将两者之间紧密联系起来，因此在同一分析框架内进行分析有助于更为全面地把握人口集聚影响碳排放的内在机制。从指标选取来看，采用人口规模和城镇化的实证研究居多，然而这两个指标仅能部分反映人口分布的空间集中，所以对应的节能减排效应估计还包含了混杂因素的影响。尽管在城镇样本的经验研究中更多采用人口密度等集聚指标，但是用于分析其节能减排效应的文献却极为少见，这是因为当前以城镇为边界的能源消费数据统计尚不够完善，未能形成被广泛认可的碳核算方法。因此，本文从要素需求视角分析了人口集聚与碳排放之间的非线性关系，并采用省级层面的建成区人口密度来反映人口集聚。

三、模型设计与数据选取

（一）理论假设与模型构建

为了分析人口集聚对碳排放的影响，我们首先从成本最小化的能源需求函数开始，［27］然后再利用综合能源因子建立碳排放的决定方程。［28］假定生产过程投入资本、劳动和能源三种要素，进一步引入人口集聚的正外部性，那么可以设定如下Cobb-Douglas成本函数：

其中C(·)为成本函数，全要素生产率A、人口集聚D与成本之间呈反向变动关系，Q为产出水平，PK、PL和PE分别表示资本价格、劳动价格和能源价格。α、β和γ分别对应三种投入要素的产出弹性，且满足规模报酬不变，即α+β+γ=1。

根据Shephard′s 引理可知，在给定支出函数的条件下，对价格求偏导数可以得到对应投入要素的Hicks需求函数。用E表示能源需求，那么这里对式（1）求能源价格的偏导数便可以得到如下能源需求函数：

由于生产者在长期均衡条件下的总收益等于总成本，所以产品价格PQ取决于三种要素的投入价格，即此外，在给定能源结构时，碳排放与能源消耗具有线性关系，即CE=F×E。其中CE表示碳排放，F为综合能源排放因子，当能源结构越低碳时其值越小，反映了能源结构对碳排放的影响。将式（2）带入碳排放等式可得：

用N表示人口总量，那么可进一步定义pc=CE/N为人均碳排放，pq=Q/N为人均产出，ep=PE/PQ为实际能源价格。对式（3）两边同时除以人口总量并取自然对数，我们便可以进一步得到如下人均碳排放的因子表达式：

由式（4）我们可以得到如下结论：人均碳排放取决于经济发展水平、高碳能源结构、实际能源价格、全要素生产率以及人口集聚水平，其中前两个因素与人均碳排放呈正向变动关系，后三个因素则呈反向变动关系。进一步将式（4）随机化为如下的基准经验模型为：

其中pc、pd、pq、ep、es和A分别表示人均碳排放、人口集聚、经济发展、能源价格、能源结构以及全要素生产率，β0-β5分别为对应的回归参数，ε为残差项。

根据经典理论，人口集聚对节能减排的影响取决于集聚效应和拥挤效应的综合结果。借鉴邵帅等人关于经济集聚的理论分析，［1］人口集聚的节能减排效应同样存在着阶段性特征。首先，初始发展阶段的设施共享、成本降低和能源节约的集聚效应大于生产规模扩张的增排效应，从而使得人口集聚对人均碳排放表现为抑制作用。其次，快速发展阶段的人口集聚不断提升会加快生产规模扩张，能源需求急剧增加引致的增排效应会大于规模经济、技术溢出、知识共享等引致的减排效应，人口集聚主要表现为促进作用。最后，随着经济体迈入高质量的成熟发展阶段，高度人口集聚所产生的各种正外部性发挥得更为充分，同时技术进步提高、环境规制完善和产业结构升级等因素均会在不同程度上抑制排放，从而使得人口集聚表现出持续的减排效应。由此，我们提出如下理论假设：

假设1：在其他条件不变的情况下，人口集聚对人均碳排放的影响会表现出下降→上升→下降的阶段性变化特征，即二者之间呈现“倒N”型关系。

为了验证假设1，我们将人口集聚的二次项和三次项引入基准模型，当二次项的系数显著为正、一次项和三次项的系数显著为负时，“倒N”型关系成立。同时，基于环境库兹涅茨曲线理论，加入经济发展的二次项进行控制。那么，进一步将模型（5）扩展为如下面板模型：

其中i表示省份，t表示时间，ui表示省份固定效应，lnpds、lnpdc表示人口集聚对数的二次项和三次项，lnpqs则为经济发展对数的二次项，其他变量定义与模型（5）相同。本文对模型（6）采用面板固定效应进行估计，同时进行Hausman检验以评估适用性。

根据空间经济学理论，地理上相互临近省份之间的交流合作更为频繁，在发展模式、经济政策和要素配置等方面往往表现出一定的协同性，因此具有更为显著的空间依赖性特征。一方面，临近省份在节能减排政策、人口集聚模式和经济发展方式等方面可能表现出相对一致性，因此人均碳排放、人口集聚和经济发展的空间溢出主要表现为相互促进的扩散效应。另一方面，人口集聚和经济发展的正向空间溢出有助于跨区域的要素流动更加充分，从而实现整体的配置效率改善。由此，我们提出如下理论假设：

假设2：人均碳排放存在正向空间溢出，即地区间节能减排的模式表现出协同效应。

假设3：人口集聚和经济发展的空间溢出表现为扩散效应，这种扩散效应会进一步优化资源的跨区域配置效率，进而推进地区之间的节能减排。

为了验证假设2 和假设3，我们在模型（6）的基础上加入人均碳排放、人口集聚以及经济发展的空间滞后项。同时进一步加入了其他解释变量的空间滞后项，以便控制遗漏空间相关性可能造成的估计偏误。扩展后的空间面板模型如下：

其中wij为空间权重矩阵中第i行j列对应的元素，本文采用地理相邻的0-1 空间权重矩阵，当然后文也进一步采用逆经纬度距离空间权重矩阵进行了稳健性检验。wijlnXjt表示剩余其他解释变量的空间滞后项，ρ为对应的空间滞后参数。不难看出，模型（7）为空间面板杜宾模型（SDM），本文采用准极大似然法（QML）进行估计，并对其是否会退化为空间滞后模型（SLM）和空间误差模型（SEM）进行似然比（LR）检验。

此外，由于人口集聚会带来空间经济活动的集中，其外部性还会对其他经济环节产生重要影响，基于前文的阶段性特征分析，这些影响同样可能呈现非线性关系。而诸如能源结构、能源价格、能源强度、经济发展、技术进步和产业升级均会对人均碳排放产生不同程度的影响，［29］所以这些经济特征变量构成了人口集聚对人均碳排放的可能作用渠道。由此我们提出如下假设，并采用与模型（7）相同的设定形式进行估计。

假设4：人口集聚以能源结构、能源价格、能源强度、经济发展、技术进步和产业升级为作用渠道，非线性模式的综合作用结果决定了其与碳排放的“倒N”型关系。

（二）变量选取与数据说明

本文的被解释变量为人均碳排放（pc），即碳排放与人口总量之比。采用IPCC 推荐的参考方法核算所有化石能源燃烧产生的碳排放，同时扣除了工业部门作为原料使用的部分。人口为各省份的常驻人口总量。此外，我们还选择了碳排放强度（qc）作为替代指标，即碳强度为碳排放与GDP 之比，进而从生产角度进行了稳健性检验。各类能源消费数据来自《中国能源统计年鉴》中的各省份能源平衡表，能源排放因子采用中国《省级温室气体清单编制指南》（发改办气候［2011］1041 号）推荐的参考值，常住人口和GDP的原始数据来自《中国统计年鉴》，GDP调整为2000年可比价格。

人口集聚（pd）为本文的核心解释变量，考虑省域内的人口主要向城镇地区集聚，因此本文采用城镇人口密度指标来表示。为了降低地形地貌的影响，我们选择城镇常住人口与建成区面积之比进行测度。基准模型中的另外两个重要解释变量分别为经济发展（pq）和能源价格（ep），其中经济发展采用人均GDP 来表示，能源价格用燃料类商品零售价格指数来表示，二者均调整为2000 年可比价格。各省份城镇常住人口、建成区面积、人均GDP 以及价格指数均来自《中国统计年鉴》。

全要素生产率主要由制度、技术和结构等因素共同决定，为了降低遗漏变量偏误，提高模型的稳健性，本文还额外加入了一组控制变量。能源结构（es）采用各省一次能源消费中煤炭所占百分比来表示。产业升级（up）采用第三产业增加值与第二产业增加值之比来表示产业结构的高级化。技术进步（tc），借鉴文献中的常用做法采用人均授权专利数来测度。外资结构（fs），由于近年来分省份统计的外商直接投资数据已经不再公布，本文采用固定资产投资中外资所占比重进行测度。市场结构（ms）反映一个地区的市场化程度，这里采用非国有就业人员所占比重来表示。经济发展、能源价格、能源结构、产业升级和技术进步为重点考察的作用渠道变量。此外，根据Kaya 等式，［30］本文还增加了额外的渠道变量能源强度（eq），即能源消费总量与GDP之比。上述变量构造用到的原始数据全部来自《中国统计年鉴》和《中国能源统计年鉴》，基于数据的可得性和口径一致性，本文采用2000-2019 年中国30 个省份（西藏因数据缺失而被排除）的面板数据为研究样本，相关变量的描述性统计结果如表1所示。

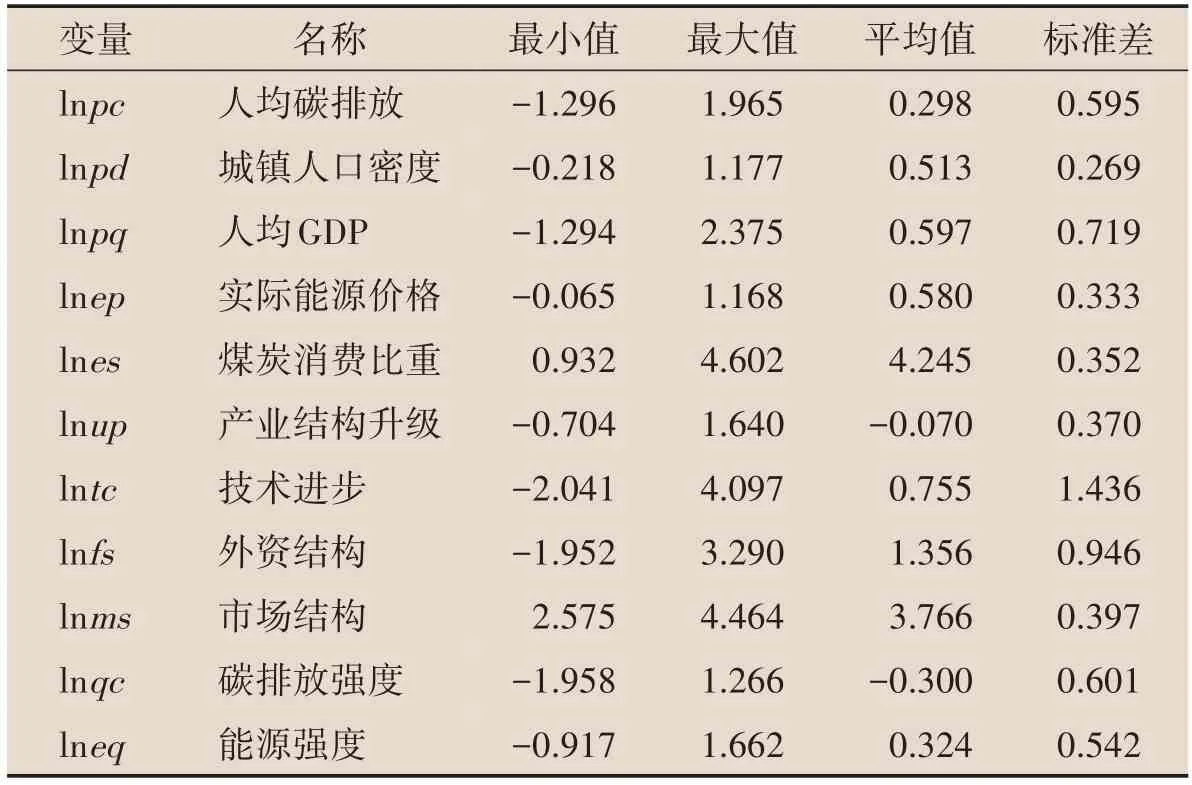
表1 变量的描述性统计结果

四、实证结果与主要发现

（一）基准回归结果分析

1.空间自相关检验

为了验证是否存在空间效应以及选择空间面板模型的必要性，我们首先采用全局莫兰指数对主要变量的空间自相关性进行检验。计算公式如下：

I为全局莫兰指数，S是所有空间权重矩阵元素的加和，n为空间单元总数，y为对应空间单元的属性值。全局莫兰指数在（-1，1）之间取值，取0值时意味着观测数值在地理上呈随机分布、彼此独立，大于0 为空间正相关，反之则为空间负相关。

表2 报告了模型核心变量人均碳排放、人口集聚、人均GDP、能源价格以及碳排放强度的全局莫兰指数，同时给出了对应的统计检验结果。在2001-2019 年期间，人均碳排放、碳排放强度以及人均GDP 的全局莫兰指数都至少在1%的统计水平上显著为正，这意味着碳排放和经济发展存在着显著的正向空间依赖性。人口集聚也表现出正向空间自相关性，2011 年以前的显著性水平均至少在10%以上，之后的空间自相关指数逐年下降，统计显著性也在持续降低，但大多数年份都至少在20%的水平上显著。综合来看，省域人均碳排放存在正向空间溢出，人口集聚和经济发展也表现出不同程度的空间扩散效应，因此假设2 和假设3 在这里得到部分验证，至于扩散效应对人均碳排放的影响还有待提供更加充分的检验证据。

表2 主要变量的全局莫兰指数检验结果

2.回归结果分析

表3报告了普通面板FEM模型、空间面板SEM、SLM以及SDM模型的估计结果，从Hausman检验来看，除SEM 模型以外均至少在5%的显著水平上拒绝随机效应，因此采用省份固定效应是合适的。随着空间效应控制的强化，模型（1）至（3）的人口集聚一次项系数均显著为负，二次项系数显著为正，但是三次项都未能通过显著性检验。这说明忽视人口集聚、经济发展乃至其他经济变量的空间效应可能造成较高的参数估计偏误。模型（4）为控制更多空间效应的SDM 模型，可以看出人均碳排放的空间滞后项系数及其显著性水平都获得了明显提升，人口集聚的三次项系数也变得非常显著。为了进一步降低遗漏变量可能产生的内生性估计偏误，我们在模型（4）的基础上加入了一组额外的控制变量，模型（5）的估计结果表现出更为优良的统计特征。此外，无论是模型（4）还是模型（5），LR 检验均在1%水平上拒绝原假设，即SDM 模型不能退化为SLM 或SEM 模型。因此，在下文的分析中将重点关注引入控制变量后的面板SDM模型估计结果。

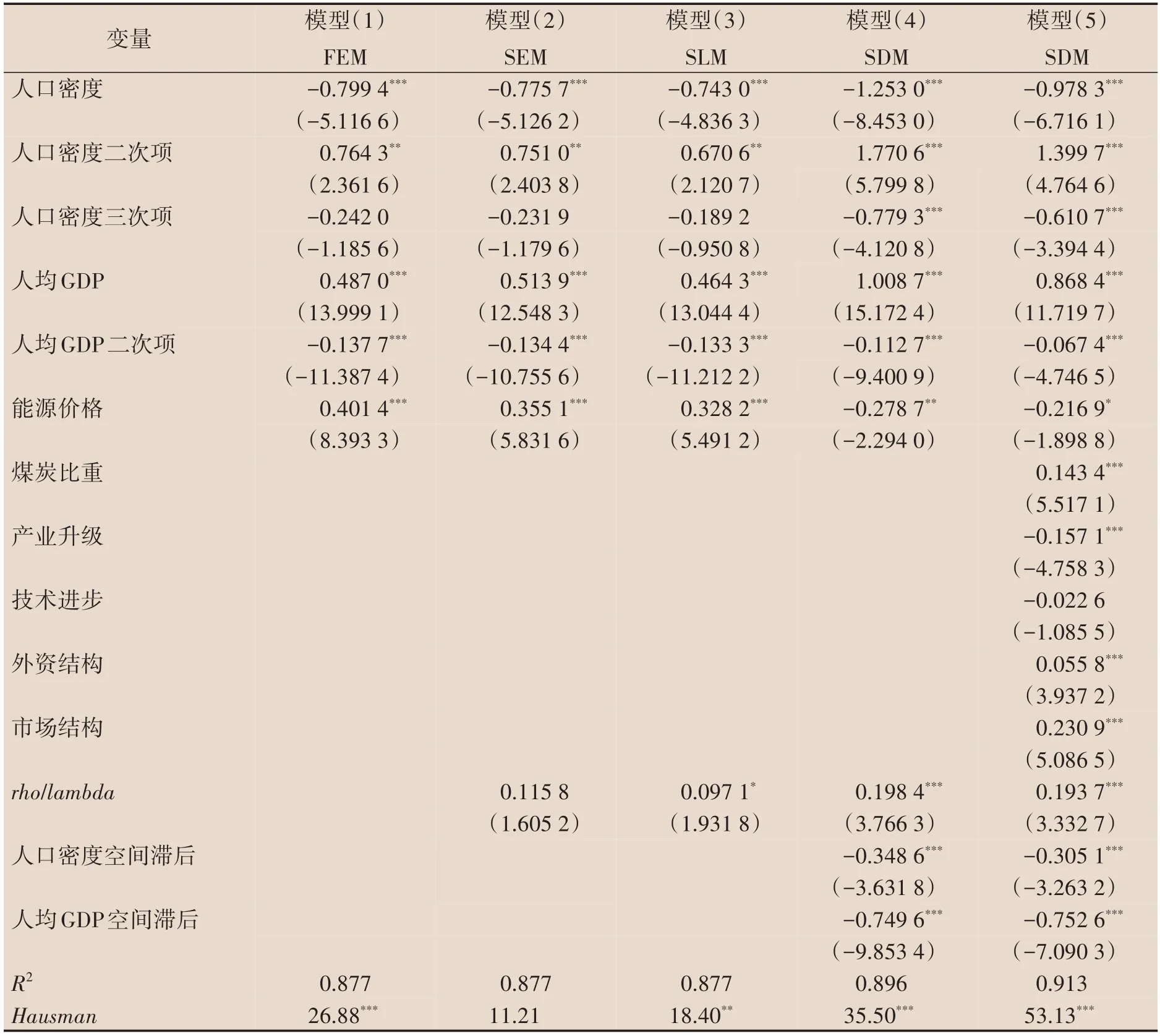
表3 人口集聚影响碳排放的基准回归结果

由模型（5）的结果可知人口集聚的一次项、二次项和三次项均在1%的水平上统计显著，回归系数的符号依次为负、正和负，表明人口集聚与人均碳排放之间确实存在显著的“倒N”型曲线关系，验证了假设1 提出的阶段性特征。具体而言，当集聚水平低于1.72 万人/平方公里的拐点时，人口集聚对人均碳排放产生抑制效应，此时的人口集聚程度处于相对较低的初始发展阶段，设施共享、成本节约以及知识溢出等集聚效应要显著大于需求增加引致的碳排放规模效应。当集聚水平超过1.72 万人/平方公里并小于2.69万人/平方公里时，人口集聚对人均碳排放产生增排作用，此阶段人口集聚程度处于相对较高的快速发展阶段，拥挤效应变得越发突出，因此城镇人口规模加速扩张造成的碳排放规模效应会显著大于人口集聚效应。当人口集聚水平越过第二个拐点值2.69万人/平方公里时便进入了成熟发展阶段，此时城镇人口规模扩展变得相对缓慢，但是节能减排的专业化分工、集中监管、技术进步和产业结构升级等集聚外部性会进一步得到充分发挥，进而对人均碳排放的抑制效应占据主导。结合样本数据来看，21世纪初的内蒙古、辽宁、黑龙江、甘肃、宁夏和新疆6省区的人口集聚水平低于第一拐点，上海、重庆、福建、贵州和云南5 省市超过了第二个拐点值，其他省份均处于“倒N”型曲线的中间阶段。自2005 年前后开始，虽然各省份的城镇人口规模在加速扩大，但是大多数省份的城镇建设用地面积增长速度更快，人口城镇化明显滞后于土地城镇化，致使人口集聚水平开始呈现出不同程度的下降趋势。截止到2019 年人口集聚处于中间增排效应阶段的仅为河北、山西、上海、河南、湖南、云南6 省市，其他省份全部滑入减排效应的第一阶段，而且大多数省份都较为临近拐点值。邵帅等人关于经济集聚节能减排效应的研究表明仅有少数省份经济集聚越过第二拐点进入减排的成熟阶段，其他省份均处于增排效应的第二阶段。［1］由此可见中国省份的人口集聚要滞后于经济集聚，致使二者的节能减排效应所对应的发展阶段并不完全一致，这与王金营和王晓伟的结论一致。［21］此外，区别于部分文献的“正N”型关系结论，我们在样本数据和指标选取上存在明显不同。一方面是我们采用了更长时间跨度的省份面板数据，支持非线性关系识别的样本量相对更大；另一方面是本文采用了城镇常驻人口与建成区面积之比来测度人口集聚，区别于大多数文献利用总人口与省辖区面积之比的指标，由于省辖区面积受地形地貌的影响较大且数量固定，因此后者对人口向城镇地区流动、集中的趋势反映有所不足。

从空间效应的估计结果来看，人均碳排放的空间滞后项系数在1%水平上显著为正，这表明临近地区之间的碳排放行为存在策略性竞争效应，如果一个地区发展绿色经济和推行节能减排，那么相邻地区也会进行效仿和学习，从而使得地区间的人均碳排放在空间上表现出协调一致性，假设2 的空间协同效应被进一步证实。前文的全局莫兰检验结果已经证实人口集聚和经济发展存在空间扩散效应，这里的人口集聚和人均GDP 的空间滞后项系数均在1%的统计水平上显著为负，表明二者的空间扩散效应有利于降低临近地区的人均碳排放水平，假设3的空间抑制效应被进一步证实。随着区域一体化程度的不断提高，相互临近省份之间的经济发展交流越来越频繁，更易于形成产业联动互补、技术协同创新，充分的人员往来和要素流动有利于提高整体发展效率，进而使得临近省份的人口集聚和经济发展对本地的人均碳排放表现出一定的抑制效应。

从控制变量来看，人均GDP 的一次项系数为负、二次项系数为正，而且均在1%的统计水平上通过了显著性检验，这表明中国省域的人均碳排放与经济发展之间存在“倒U”型环境库兹涅茨曲线关系。实际能源价格水平的系数在10%水平上显著为负，表明能源价格上涨具有节能减排效应，实际价格越高，人均碳排放越小。技术进步的系数符号虽然为负但却不显著，这表明当前的整体技术进步偏向仍然以提高生产率为主，绿色技术偏向尚不明显，进而使得技术进步的减排效应并不明显。产业升级的系数符号为负且高度显著，表明以第三产业比重不断提升为特征的产业结构调整升级具有节能减排效应，能够实现人均碳排放水平的显著降低。此外，能源结构、外资结构和市场结构的系数均在1%统计水平上显著为正，这些经济特征变量对人均碳排放表现出了增排效应。显然，一次能源消费中煤炭比重提升会造成更多碳排放，外商投资比重提高对人均碳排放的增排效应证实了污染避难所假说。以非国有就业人员占比衡量的市场化程度未能表现出减排效应，这可能在一定程度上表明市场化并不是在所有经济领域总是有效的，国有企业在节能减排的执行效果上更为突出。

（二）稳健性的测试结果

由于人口集聚所引起的消费水平、消费模式变化以及对生产活动的影响，前文主要从消费视角考察了人口集聚与人均碳排放的非线性关系。作为稳健性检验，本文进一步采用从生产视角度量的单位产出碳排放（碳排放强度）这一指标作为被解释变量，并基于与前文相同的实证策略对人口集聚的节能减排效应进行考察。此外，我们还采用反距离权重矩阵替换空间邻接矩阵进行了重新估计，删除4 个直辖市估计了所有省区的平均效应，相关稳健性检验结果如表4 所示。模型（1）和（2）为采用碳排放强度指标的估计结果，模型（3）和（4）为采用空间反距离权重矩阵的估计结果，模型（5）和（6）为提出直辖市干扰后的省区样本估计结果。人口集聚一次项、二次项和三次项在上述模型中都在1%统计水平上高度显著，而且系数符号依次为负、正和负，依然呈现“倒N”型曲线关系。被解释变量的空间滞后系数大都非常显著且符号与原模型保持一致，表明人均碳排放、碳排放强度具有正向空间溢出效应。人口集聚和经济发展的空间滞后系数在模型（1）至（6）中也呈现出相似的估计结果，二者的空间扩散效应依然发挥着节能减排作用。此外，剩余控制变量的系数符号及显著性也与原始模型保持了高度一致性，由此表明前文提出的假设1、假设2和假设3不仅被进一步充分证实，而且结论是非常稳健的。

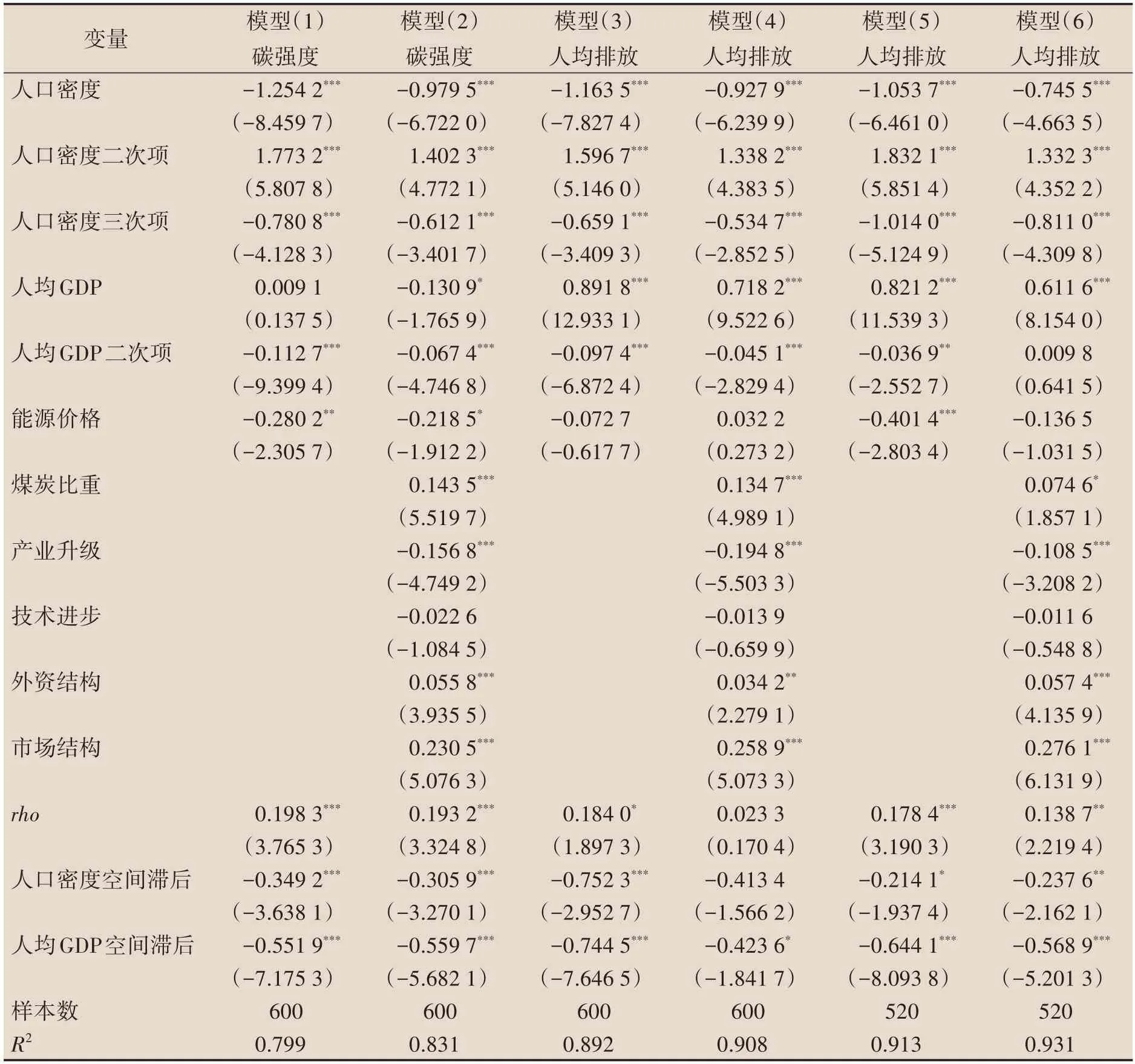
表4 人口集聚影响碳排放的稳健性检验结果

（三）多重作用渠道检验

为了进一步探讨人口集聚对人均碳排放的影响机制以及二者之间“倒N”型关系的可能成因，我们接下来采用与前文相同的模型设定考察了人口集聚对能源结构、能源强度、能源价格、经济发展、产业升级和技术进步的非线性影响，估计结果依次对应表5中的模型（1）至模型（6）。

表5 多重作用渠道的检验结果

估计结果显示除了模型（5）以外，其他模型中人口集聚一次项、二次项和三次项系数都至少在5%的统计水平上通过了显著性检验。能源结构、能源强度、能源价格三个方程中的系数依次为负、正和负，表明人口集聚对能源利用的影响呈“倒N”型曲线关系，这与其对人均碳排放的影响方向一致，因此能源利用的渠道作用更为突出。经济发展和技术进步方程中的系数依次为正、负和正，表明人口集聚对二者的影响呈“正N”型曲线关系。人口集聚对产业升级的影响为线性关系，一次项系数在1%的统计水平上显著为正，表明人口集聚程度提高有利于产业结构的调整升级。综合上述方程的检验结果来看，人口集聚对渠道变量的影响主要以非线性关系为主，能源利用的渠道作用占据主导，因此这种综合作用结果决定了人口集聚与人均碳排放之间的“倒N”型曲线关系，假设4得到了证实。此外，上述渠道变量在对应方程的空间滞后项都在1%统计水平上显著为正，表明能源结构、能源价格、能源强度、经济发展、产业升级和技术进步具有空间溢出或空间扩散效应。人口集聚的空间效应对本地的能源结构、产业升级和技术进步表现为促进作用，对能源强度和经济发展表现为抑制作用，而对本地能源价格的影响不显著。

五、结论与启示

本文从生产者均衡视角分析了人口集聚与人均碳排放之间的关系，采用2000-2019年中国30个省份的面板数据，利用空间面板模型进行了系统而稳健的估计和检验，进一步探讨了人口集聚对节能减排的作用渠道。本文主要得出以下结论：

首先，中国各省份人口集聚对人均碳排放的影响呈现“倒N”型关系。人口集聚的节能减排效应取决于集聚效应和拥挤效应的双重影响，综合作用方向表现为阶段性特征。在人口集聚水平较低的初始阶段表现为减排效应，在人口集聚快速提升的发展阶段表现为增排效应，在人口集聚水平较高的成熟阶段则进一步表现为减排效应。从当前发展水平来看，仅有少数省份的人口集聚进入增排阶段，其他剩余省份全部处于减排效应的第一阶段，并且大多数省份离第一拐点值较近。整体而言，各省份的人口集聚速度要明显滞后于经济集聚速度，因此发挥城镇人口集聚的节能减排效应仍然有较大的提升空间。其次，中国省份间的人均碳排放、人口集聚和经济发展存在显著空间溢出效应。节能减排行为的策略性竞争会促进地区间的相互模仿和学习借鉴，进而使得人均碳排放在空间上表现为协同效应，即周边省份的人均碳排放增加也会加剧本地排放水平的提升。人口集聚和经济发展表现为空间扩散效应，这种扩散效应能够加速地区间的人员往来和要素流动，进而提升全局的经济发展效率和能源利用效率，因此二者的空间溢出特征具有减排效应。最后，能源利用和经济发展是人口集聚影响人均碳排放的作用渠道。其中，人口集聚对能源结构、能源强度和能源价格的影响均呈现“倒N”型关系，人口集聚对产业升级的影响呈正向线性关系，对人均GDP 和技术进步的影响则均呈现“正N”型关系。人口集聚对能源利用的作用强度更大，因此上述渠道变量的综合作用结果便决定了人口集聚与人均碳排放的“倒N”型关系。

基于文章的实证结论和主要发现，为了进一步推进人口集聚与节能减排的协调发展，本文提示在以下两个方面有待决策者参考。第一，推动以发挥人口集聚效率为特征的城镇化高质量发展，助力“碳达峰碳中和”战略实施。近年来涌现的城市病问题并不单单是人口集聚导致的拥挤效应，而更多是城市管理效率低下、空间格局不合理所致。［31］实际上大多数省份的土地城镇化都要明显快于人口城镇化，破解拥挤效应如果只是单纯依靠扩张城镇建设用地面积，那么首先伴随的也是集聚效应的损失。因此，应该严格管控城镇建设用地面积扩张，将重点放在优化空间格局和提升管理水平上来。第二，充分发挥人口集聚中心区的辐射作用，促进地区间人员往来、要素流动以及产业调整的联动发展。随着区域一体化程度的日益提高，人口集聚、经济发展和节能减排的空间溢出效应日益增强。实现城镇人口集聚与节能减排的协调发展，应充分发挥以大城市为辐射中心、以周边县城为重要载体的联动机制，区域内部产业要合理布局，避免要素拥挤以及过度竞争，进而推动整体绿色转型发展。