内河航道宽度确定若干方法探索
2022-10-10王家宏王伟军艾万政
王家宏,王伟军,艾万政
(浙江海洋大学,浙江 舟山 316022)
航道是船舶通航的载体,其主要功能就是为船舶通航服务。相关统计资料表明,大约15%的交通事故是由于航道缺陷造成的。因此合理改造航道,科学布置航道浮标,是确保船舶通航安全的重要前提之一。对于内河航道浮标设置而言,最重要的是航道两边的边界浮标设置问题。航道两边界浮标之间的间距安排,与航道宽度密切相关。如果航道两边界浮标之间的距离设置较大,就会浪费航道资源;如果航道两边界浮标间距过小,就会影响到船舶的通航安全。因而航道边界浮标设置力求合理科学。众所周知,影响内河航道宽度的主要因素包括代表船型船舶的航迹带宽度、船间间距、船岸间距和附加宽度等。目前我国内河通航标准对我国内河航道宽度都有明确的界定[1-3]。在该标准中,船舶的航迹带宽度、船间间距和船岸间距等参数都是以代表船型尺度(船长、船宽)来确定的。毋庸置疑,船舶的航迹带宽度与船舶的长度、宽度和偏航角相关,航迹带宽度完全可用通航船舶的长度和宽度来确定。而关于航道的附加宽度,内河通航标准中并没有明确界定,尤其是天然弯曲航道的附加宽度,标准中只是提到,可考虑以顺直航道宽度为基础且适当加宽,但究竟以加宽多少为标准,内河通航标准中并没有直接界定。不少学者认为,航道的附加宽度主要是风、流等因素对船舶造成的漂移量。有关顺直航道的风致漂移量和流致漂移量,目前研究成果较多,在顺直航道浮标设置中可直接借鉴运用[4-7]。但是对于弯曲航道而言,由于弯道环流的流向、流速均随水深的变化而变化,因此弯道船舶的流致漂移量如何确定,则有待于进一步研究[5]。关于船间间距、船岸间距,其大小与船间效应、岸壁效应密切相关,而船间效应、岸壁效应是2个非常复杂的问题,其不但与通航船舶的尺度相关,而且还与水流条件密切相关。因此单纯以船舶尺度去确定船间间距和船岸间距,明显显得不够合理。为此,关于内河航道宽度的确定,重点是要解决船间间距、船岸间距及弯道流致漂移量等问题。由此看来,有必要紧紧围绕船舶通航安全去讨论船间间距、船岸间距及弯道流致漂移量等问题,以便为内河航道宽度的确定奠定基础,以减少交通事故发生的概率。
1 船间间距和船岸间距的确定方法
1.1 概率论确定方法
船间效应和岸壁效应非常复杂,二者分别与船间间距和船岸间距密切相关。目前关于船间效应和岸壁效应,虽然研究成果较多,但这些成果多数只限于定性分析层面,关于船间效应和岸壁效应的数学模型或经验公式,目前几乎还没见到。由于船间效应和岸壁效应的复杂性,所以也很难从定量层面去确定船间间距和船岸间距的大小。如果换位思考,概率论的相关知识为此提供了较好的解决办法。
图1表明了相遇船舶的状况。x1表示;若下水船舶偏离航道轴线,其概率值可用x2表示。x1和x2无关,且都服从正态分布,且x1和x2是随机变量,也就是说某船偏离航道轴线是随机的,与另一条不相关。图1表明
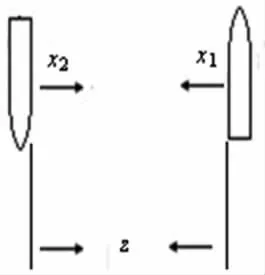
图1 相遇船舶

式中:z0为相会船舶应保持的合理间距。式(1)说明,如果z>0,即x1+x2

则综合x1的正态分布函数f(x1)及x2的正态分布函数f(x2),可以得到

式(3)可改写为
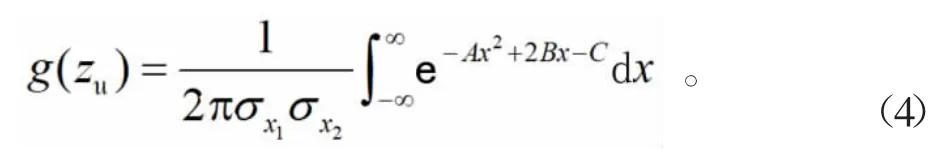
式(4)中

应用伯努利-泊松间距公式,可得到

从式(8)可以看出,正态分布规律适用于2条相遇船舶的横间距分布。因此相遇船舶发生碰撞概率可以表达为
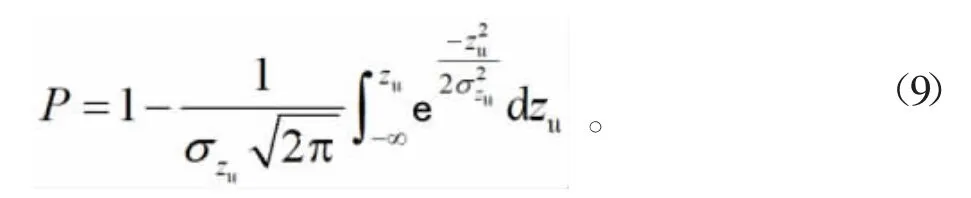
如果设定:dzu=σzu v,则式(9)可以变形为

引入拉普拉斯参数
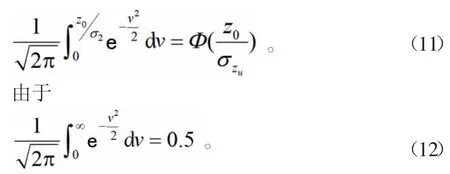
结合式(10)、式(11)和式(12)可得

式(13)明确表明,在已经知道航道事故概率P的情况下(此值可根据航道设计要求预先设定),则可得到相应的z0,此时船间间距也就完全确定。例如,如果在航道规划时,预计船舶碰撞概率预定为0.005,即P=0.005。则按照式(13),可以认为

根据式(13)可求解得到

如果认为船舶上、下水航行准确性一致,在这种预定情况下,可设置σx1=σx2,因此式(15)经过推导可得到

相关研究表明,均方差σx与船舶的尺度有关,其大小可以根据航道内多年船舶通航观测数据确定。按照上述同样的方法,船岸间距也完全可用类似的方法确定。但此方法要基于大量统计数据,对于新开辟的航道不一定完全适用。对于老航道的改进,则还有一定的指导意义。
1.2 船舶领域理论确定方法
日本籍学者藤井弥平在详细调查日本近海船舶的相对位置时,在经过认真分析的基础上,得出了一种模型,即船舶领域模型。船舶领域模型理论认为,船舶领域是以船舶为中心的椭圆形区域,该区域的长轴是船舶中心纵轴线,而短轴是与长轴相垂直的船舶中心的横轴线。船舶领域的尺度如下:长轴大约为7倍船长,短轴为3倍船长,而船舶位于该领域的中心。在一般的船舶追越局面中,相对水域足够,被追越船的船舶领域尺度可适当认为较宽,船舶领域长轴取8倍船长,短轴取3.2倍正横距,这有利于船舶防撞。如果船舶航行到速度受限的水域,如港区、狭水道和狭窄海峡,此时船舶领域尺度可能大大减小,此时船舶领域的长轴一般取6倍船长,短轴一般取1.6倍正横距。
Goodwin在认真研究藤井弥平船舶领域模型的基础上,最终创立了一套改进的船舶领域模型,该模型较好地适用于宽阔水域(该模型如图2所示)。其运用船员培训机器及伦敦帝国理工学院雷达模拟器,进行了大量的船舶碰撞方面的试验,并对北海南部区域的船舶交通进行调查,其调查方法与日本学者藤井弥平类似,并最终认为,《1972国际海上避碰规则》对船舶的行动有着较大的影响。从避碰规则来看,规则按照来船方位区别,对不同的避让行动进行了规定。因而可见,藤井弥平的船舶椭圆形领域模型有着不完善的地方,船舶领域的几何图形不应该是对称的。Goodwin在总结船舶号灯显示范围的基础上,重新划分了船舶领域,其领域范围如图2所示。其船舶领域模型充分考虑了《1972年国际海上避碰规则》对船舶行动行为的要求。无论是藤井弥平船舶领域模型还是Goodwin的船舶领域模型,都是通过分析大量数据得出的,对船舶安全航行具有指导意义。在确定内河船间间距及船岸间距时,也可以参考船舶领域理论,将船舶横向领域的最大范围作为船间间距及船岸间距的参考量。船舶领域可以用来设计航道的宽度,但该理论是日本学者统计日本航道情况而得出的,对于其他航道是否适用,还有待于进一步探索。因为航道宽度的确定与航道特定水流条件密切相关,船舶领域理论虽然有一定的指导意义,但其普遍适用性还需要进一步验证。

图2 Goodwin模型
2 弯道流致漂移量确定方法
在天然弯曲航道存在弯道环流,这种环流正是引起船舶横向漂移的重要因素。在确定航道宽度时,应该将弯道环流引起的船舶横向漂移量考虑进去,这样有利于保证船舶运行安全。弯道环流与普通的横流不同之处在于:弯道环流的面流流向凹岸,随着水深的增加,环流逐步减小,当水深到达某一深度时,环流开始反向(从凹岸流向凸岸)并逐渐加大。弯道环流的这一特性,决定了其对吃水不同船舶产生的横向漂移量不一样。弯道环流可用公式表示为
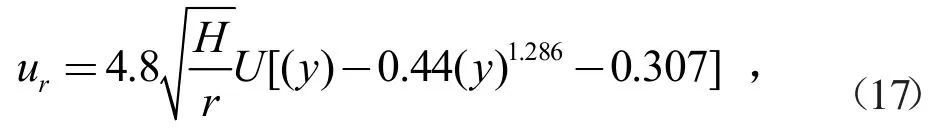
式中:U为弯道纵向流速;H为弯道水深;y=z/H为相对水深用(水深起算点被认为从河底开始);r为弯道曲率。在弯道存在弯道横流,其底流流向凸岸,面流流向凹岸,面流和底流流向相反,因而,船舶吃水为d时,通过数学推导可知,作用于船体上的平均弯道环流流速可表达为

式中:ud为船体上的平均弯道环流流速。综合式(17)及式(18),可以导出
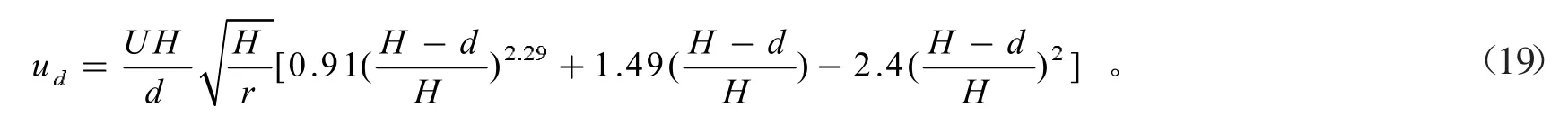
式(19)表明,作用在船体上的平均弯道环流流速由弯道曲率、平均纵向流速、弯道水深和船舶吃水共同确定。将式(19)应用到顺直航道船舶流致漂移量公式中,即可计算出弯道船舶流致漂移量。该方法本文相关作者曾在别的文献中提及过,但计算程序较为繁琐,适用性还不够理想。
3 船桥间距确定方法
内河桥区航道往往也是事故多发地段。对于桥区航道而言,桥墩与航道边界浮标之间的间距也是航道宽度设计时的重要考虑因素。内河航道建桥以后,由于桥墩的存在,水流结构变得复杂,航行安全隐患也增加。桥墩附近的水流结构如图3所示。一般认为,桥墩紊流漩涡区是船舶通航应回避的区域[7-8]。因此也有人认为桥区航道应布置在桥墩紊流漩涡区之外,也可以说,桥墩紊流漩涡区的横向最大范围应是船桥之间应保持的最小距离。关于桥墩紊流漩涡区范围,相关研究较多,可选用适当的经验计算模型确定,计算确定的桥墩紊流漩涡区范围,完全可应用到桥区航道宽度设计之中。但桥墩紊流是非常复杂的问题,从通航的角度如何确定其范围,相关专家说法不一。因此关于桥墩紊流对通航的影响,有待于科学试验的验证。

图3 桥墩水流结构
4 结论
内河航道宽度布置涉及到船舶的通航安全。对于内河航道宽度而言,最关键的是如何确定船间间距、船岸间距、弯道流致漂移量及船桥间距。而船间间距、船岸间距、弯道流致漂移量及船桥间距与多种影响因素相关,难以单纯从定量角度去确定。本文结合船舶操纵特性,从概率论角度和船舶领域理论角度提出了确定船间间距和船岸间距的方法;从水动力学角度提出了弯道流致漂移量确定方法和船桥间距确定方法。本文的以上研究方法和手段,为研究其他航道问题提供了一种全新的视野,但相关方法也有其局限性,需要进一步研究。
