基于PTMD的双主梁钢-混组合梁桥车-桥耦合振动控制
2022-10-10李德安王佐才王慧光金大帅
李德安, 王佐才,2, 王慧光, 金大帅
(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.土木工程防灾减灾安徽省工程技术研究中心,安徽 合肥 230009)
在中小跨径桥梁中,钢-混组合梁通常采用工字钢作为主梁形式[1]。工字钢梁具有结构美观简洁、受力特点明确、施工方便、综合造价低等诸多优点,因而获得了相对广泛的应用[2]。目前,钢-混组合梁的研究主要集中在截面形式的选择及设计参数敏感性等方面[3],而对钢-混组合梁桥车-桥耦合振动研究相对较少,特别是针对双主梁钢-混组合梁桥的相关研究很少。
由于工字钢梁竖向弯曲刚度较小,2片工字钢主梁在行车荷载作用下会产生剧烈的振动,从而使桥梁结构对车-桥耦合振动的响应较为明显,有可能加剧桥梁结构的损伤,影响使用寿命,因此,对双主梁钢-混组合梁桥进行车-桥振动控制研究具有较重要的意义。
调谐质量阻尼器(tuned mass damper,TMD)是一种离散型阻尼装置[4],常用于结构被动控制,广泛应用于桥梁结构振动控制中。文献[5]研究了两自由度模型TMD的最优参数,大量相关研究主要集中在优化TMD参数以及抑制风荷载和地震荷载作用下的桥梁振动[6-7],而利用TMD来抑制移动车辆荷载作用下钢-混组合梁桥振动的研究较少。碰撞调谐质量阻尼器(pounding tuned mass damper,PTMD)是一种新型减振装置,在PTMD的设计中,阻尼器由可移动的质量块和附加的限位装置组成,该限位装置能够限制质量块的振动,其表面的黏弹性材料可以通过冲击或碰撞耗散能量。与传统的TMD系统相比,PTMD有效降低了结构的振动和阻尼器自身的安装成本,相对容易实现和维护[8-9];此外,PTMD拓宽了阻尼器的有效减振频带,具有更大的能量耗散能力,对系统不确定性的响应更为稳健[10]。
本文针对双主梁钢-混组合梁桥行车振动问题,设计一种通过调谐质量块与黏弹性层之间的碰撞来耗散能量的PTMD,以减小车辆引起的桥梁振动;结合桥梁和车辆的运动方程,建立车-桥-PTMD耦合系统运动方程;建立某双主梁钢-混组合梁桥的有限元模型,并进行动力特性分析;考虑路面条件,基于三维车辆模型、桥梁模型和PTMD系统建立车-桥-PTMD耦合系统的仿真模型,并研究本文设计的PTMD对该双主梁钢-混组合梁桥的减振效果。
1 车-桥-PTMD耦合系统运动方程
车-桥-PTMD耦合系统力学模型如图1所示。车辆模型采用整车空间模型和多刚体系统模型,考虑二系悬挂,以便更全面地、比较真实地模拟实际车辆动力特性;桥梁模型采用有限单元法,在研究车-桥耦合竖向振动时,由于桥梁下部结构的竖向刚度比桥跨结构大得多,故将下部结构模拟成刚体。

图1 车-桥-PTMD耦合系统力学模型
1.1 车辆与桥梁运动方程
考虑车辆和桥梁不耦合时的振动方程,车辆和桥梁是2个相互独立的自由振动系统。车辆的运动方程为:
(1)
其中:Mv、Cv、Kv分别为车辆的质量、阻尼和刚度矩阵;xv为车辆的垂直位移矢量;Fv为作用在车辆上的车轮-道路接触力矢量。
桥梁运动方程为:
(2)
其中:Mb、Cb、Kb分别为桥梁的质量、阻尼和刚度矩阵;xb为桥梁所有自由度的位移矢量;Fb为作用在桥梁上的所有外力的矢量。
1.2 PTMD运动方程
PTMD安装在桥梁结构的设计位置,例如其响应成为最大值的位置。PTMD的运动方程[11]为:
(3)
其中:Mp、Cp、Kp分别为PTMD的质量、阻尼和刚度矩阵;xp为PTMD的垂直位移矢量;Fp为桥梁和PTMD相对运动产生的力;P为桥梁和PTMD垂直方向的碰撞力;Γ为碰撞力的位置矩阵;H取值为:
(4)
其中:x1为质量块的位移;x2为黏弹性材料层的位移;gp为质量块和黏弹性材料层之间的间隙。
为准确分析PTMD对桥梁结构的振动抑制效果,需要建立碰撞力模型。一些研究者通过合理的数学表达式来描述碰撞力,以研究不同结构之间的碰撞现象,并提出多个碰撞力模型来模拟结构的碰撞[12],其中,基于赫兹接触单元和非线性阻尼器的模型考虑碰撞过程中能量的耗散,本文采用该碰撞力模型。桥梁和PTMD之间的碰撞力[13]表达式为:
(5)
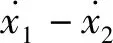
(6)
(7)
其中:m1、m2为2个碰撞体的质量;e为恢复系数;ξ为与e相关的碰撞阻尼比。e的定义为碰撞后(最终)相对速度之间的关系,可以通过反弹试验测得,即用钢球的初始高度和钢球与平板碰撞后的反弹高度来确定,e=0表示完全塑性冲击,e=1表示完全弹性冲击。
1.3 车-桥-PTMD耦合系统运动方程
利用桥梁与轮胎接触点处的位移关系和相互作用力关系,结合桥梁与车辆的运动方程,可以建立车-桥-PTMD耦合系统的运动方程,即
(8)
可采用Newmark逐步积分法对(8)式进行求解,进而得到结构的振动响应。
2 钢-混组合梁桥减振装置
本文基于TMD减振原理,设计一种通过调谐质量块与黏弹性层之间的碰撞来耗散能量的PTMD,如图2所示。PTMD具有与常规TMD类似的可移动质量块、弹簧、阻尼器及表面被黏弹性材料覆盖的限位装置,以限制质量块的冲程,并通过冲击或碰撞耗散能量。整个装置分为3个部分,由中间的TMD与两边的限位装置组成。TMD质量块的冲程受到外部激励的影响,当桥梁结构受到较小的激励时,其动力响应也较小,质量块产生的冲程小于其与限位装置之间的间隙,此时尚未发生碰撞,PTMD的减振效果与TMD相同,即通过谐振所引起的质量块运动来消耗能量;当外部激励较大,质量块的冲程超过其与限位装置之间的间隙时,两者发生碰撞会消耗动能,从而降低桥梁结构的振动。

图2 PTMD装置示意图
3 算例分析
算例采用某高速公路路段1座4×35 m双主梁钢-混组合梁桥,其基本截面尺寸如图3所示(单位为mm)。预制桥面板采用C40混凝土和PVA纤维混凝土,工字钢主梁采用Q345D碳素结构钢,桥面宽度为13 m,主梁间距为7.2 m。

图3 钢-混组合梁桥基本尺寸
3.1 桥梁有限元建模及动力特性分析
利用通用有限元软件ANSYS建立该双主梁钢-混组合梁桥有限元模型,得到该桥的质量、刚度和阻尼矩阵。混凝土桥面板采用solid65单元,工字钢梁和横隔梁均采用shell181单元,共有54 780个节点、44 080个单元。钢-混组合梁桥有限元模型如图4所示。

图4 钢-混组合梁桥有限元模型
基于有限元模型对结构进行模态分析,计算得到结构前2阶竖弯频率分别为2.78、10.74 Hz,结构前2阶竖弯振型如图5所示。

图5 钢-混组合梁桥模型振型
3.2 钢-混组合梁桥现场试验
钢-混组合梁桥试验现场与加速度传感器实物图片如图6所示。

图6 梁桥试验现场与传感器实物图片
为了解该钢-混组合梁桥实际工作状态下的振动特性,在该桥处于运营状态下进行现场试验,在边跨和中跨工字钢梁下翼缘沿四等分点等间距布置加速度传感器,测试主梁的竖向加速度,得到主梁在移动车辆荷载激励下的振动响应,并进行工作模态参数识别,即可得到桥梁结构的振动特性。
利用解析模式分解算法对实测加速度数据进行去噪处理,分别对低于0.2 Hz的低频成分和高于30.0 Hz的高频成分进行去噪,并对去噪后的数据进行快速傅里叶变换(fast Fourier transform,FFT)分析。基于分解后的模态响应,利用随机子空间法识别出结构的前2阶竖弯频率分别为2.74、10.67 Hz,结构第1阶阻尼比为2.48%。与结构模型前2阶竖弯频率相比较,实测频率与模型前2阶竖弯频率的误差分别为1.46%、0.66%。实测结构前2阶竖弯振型如图7所示,将其与图5中的前2阶竖弯振型进行对比,通过计算各阶模态的模态置信度(modal assurance criterion,MAC)可知,实测模态振型与有限元结果具有90%以上的相似度。
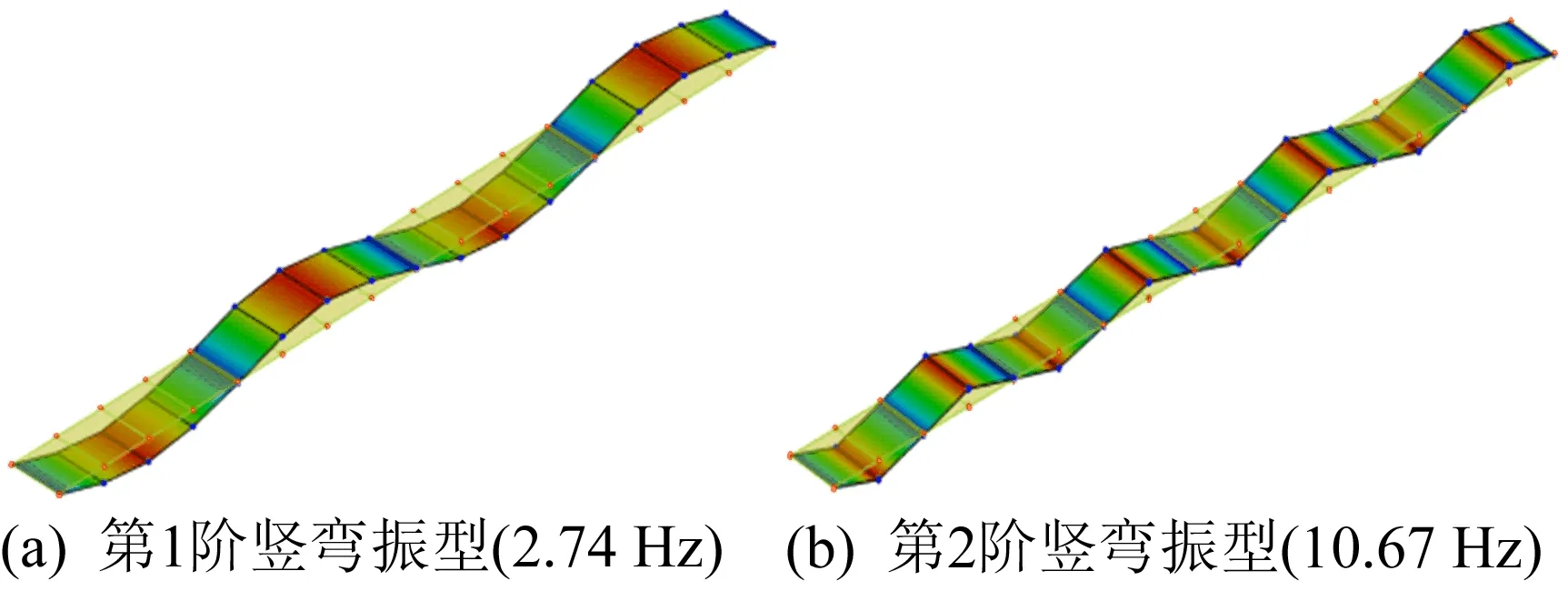
图7 钢-混组合梁桥实测振型
3.3 路面状况模型
路面状况是影响桥梁和车辆动力响应的重要因素,一般由路面不平度定性表示。路面不平度等级划分见表1所列[14]。
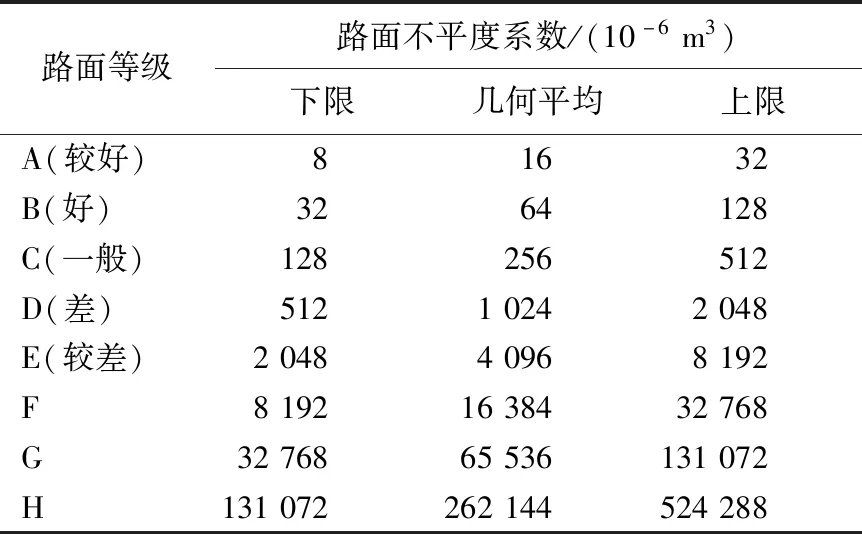
表1 路面不平度等级划分
路面不平度的时间历程可假定为零均值平稳高斯随机过程,对其最有效的描述方法之一是进行功率谱统计。路面不平度功率谱密度(power spectrum density,PSD)函数又称为均方谱密度函数,是对分布于单位频段内路面不平度测量值的均方值进行统计分析。路面不平度可以通过基于PSD函数的傅里叶逆变换来生成,能够反应路面的总体特征。不同国家根据实测数据的拟合结果,提出了各种PSD函数的规范。
本文进行车-桥耦合振动仿真分析时采用文献[14]规定的路面不平度等级C级(一般),通过对路面PSD函数求傅里叶逆变换得到路面不平度。
3.4 PTMD减振效果分析
3.4.1 PTMD参数设置及布置
为了比较TMD和PTMD的行车振动控制效果,在相同的车-桥耦合系统中分别施加TMD和PTMD,对比研究车-桥-PTMD/TMD耦合系统与无控制车-桥耦合系统的动力响应。算例中,钢-混组合梁桥的一阶阻尼比取实测值2.48%,TMD和PTMD的质量比μ均为1.0%,TMD的阻尼比为6%,PTMD的阻尼比由(7)式计算,其中PTMD的恢复系数e设定为0.5,PTMD的碰撞刚度β为20 kN/m3/2。
为了有效控制桥梁的行车振动响应,将TMD和PTMD调到桥梁的基频,并安装在位移响应最大处。为增大减振效果,以该桥边跨为研究对象,在边跨跨中及跨中前后距桥墩10 m的位置分别设置相同的PTMD/TMD减振装置。利用多体动力学软件UM建立车-桥-PTMD耦合系统仿真模型,如图8所示。
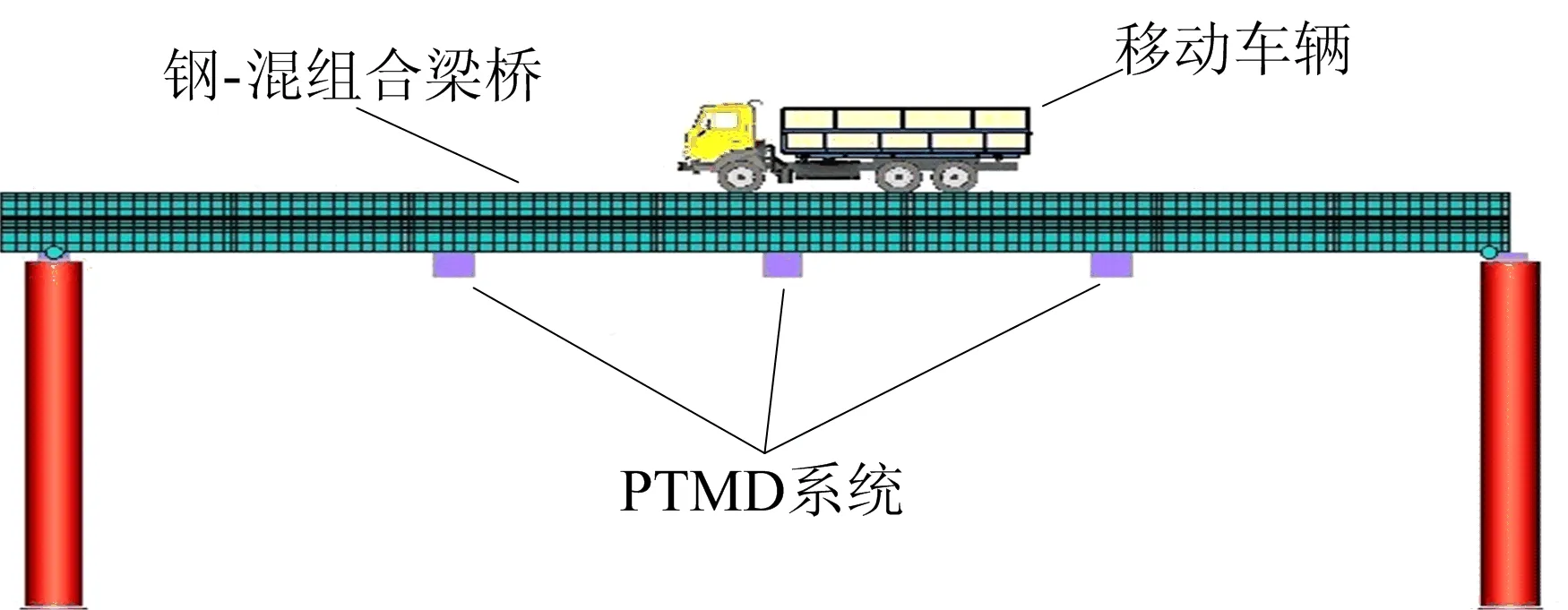
图8 车-桥-PTMD耦合系统仿真模型
3.4.2 TMD与PTMD的减振效果对比
桥梁在移动车辆荷载作用下的振动受到路面不平度、车辆质量、车速等多种因素的影响。本研究中路面不平度为C级(一般),车辆质量为55 t,车速为50 km/h,建立车-桥耦合模型进行仿真计算。移动车辆荷载作用下,安装PTMD/TMD前后,钢-混组合梁桥边跨跨中节点的位移、加速度时程曲线如图9所示。
由图9a可知,从钢-混组合梁桥竖向振动最大位移看,无减振装置时为6.814 mm,安装TMD时为5.545 mm,安装PTMD时为4.689 mm。可以看出,安装PTMD的最大位移值明显小于无减振装置和安装TMD的相应值。安装TMD对钢-混组合梁桥边跨跨中位移振动的减振率为18.62%,安装PTMD时的相应减振率为31.18%。

图9 安装减振装置前后位移和加速度时程曲线
由图9b可知,从钢-混组合梁桥竖向振动加速度峰值看,无减振装置时为1.030 m/s2,安装TMD时为0.775 m/s2,安装PTMD时为0.632 m/s2。因此,从结构跨中振动加速度看,安装TMD对钢-混组合梁桥的减振率为24.76%,安装PTMD时的相应减振率为38.64%。
综上所述,车-桥-PTMD耦合系统的动力响应明显小于无控制车-桥耦合系统的动力响应,且小于车-桥-TMD耦合系统的动力响应。本文应用的PTMD对钢-混组合梁桥的行车振动有明显的抑制效果,在其他条件相同的情况下,PTMD的减振效果与TMD相比更加明显。
3.4.3 PTMD质量比影响分析
质量比是影响阻尼器减振效果的关键参数之一,阻尼器的质量比通常为0.5%~2.0%。参考实际情况,选取0.5%、1.0%、1.5%、2.0% 4种不同质量比的PTMD,其他条件均与前述分析相同,对该桥边跨跨中竖向位移进行对比分析,边跨跨中节点位移时程如图10所示,各质量比对应减振效果见表2所列。
由图10、表2可知,PTMD的质量比对减振效果的影响较为明显,当质量比从0.5%增加到2.0%时,对竖向位移的减振率从22.74%增加到47.32%,PTMD的减振效果有显著提升。

图10 不同质量比下的位移时程曲线
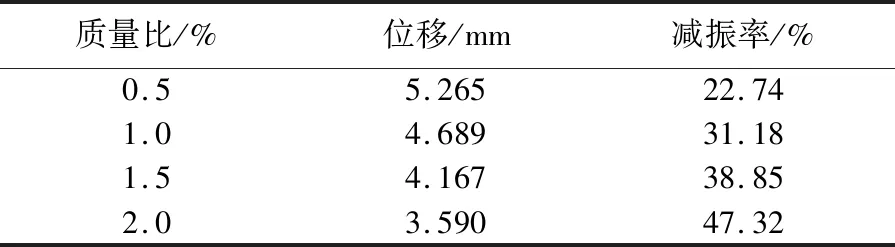
表2 不同质量比下的减振效果对比
3.4.4 PTMD碰撞刚度影响分析
碰撞刚度β也是模拟碰撞力的关键参数,其值取决于碰撞物体的材料属性和几何形状。根据实际情况,β通常为10~30 kN/m3/2。选取10、20、30 kN/m3/23种情形下的PTMD,其他条件均与前述分析相同,对该桥边跨跨中竖向位移进行对比分析,不同β下的减振效果见表3所列。
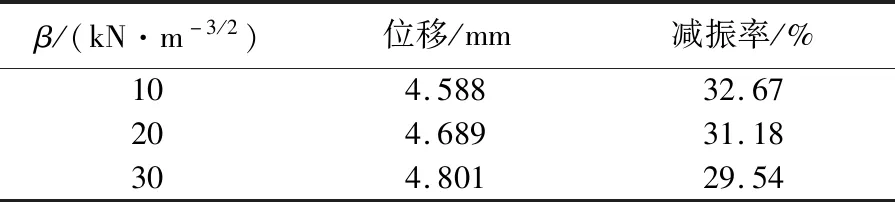
表3 不同β作用下的减振效果对比
由表3可知,β的变化对PTMD的减振效果影响不大,当β从10 kN/m3/2增加到30 kN/m3/2时,对竖向位移的减振率仅从32.67%降低到29.54%,PTMD的减振效果无明显变化。
4 结 论
(1) 本文设计的PTMD对双主梁钢-混组合梁桥的行车振动有明显的抑制效果,在其他条件相同的情况下,安装TMD、PTMD对位移的减振率分别为18.62%、31.18%,PTMD有更好的减振效果。
(2) PTMD的质量比对桥梁结构行车振动的控制效果有明显影响,当其质量比从0.5%增加到2.0%时,对位移的减振率从22.74%提高到47.32%,减振效果明显提升。
(3) PTMD的碰撞刚度对桥梁结构行车振动的控制效果没有明显影响,当其碰撞刚度从10 kN/m3/2增加到30 kN/m3/2时,对竖向位移的减振率仅从32.67%降低到29.54%。
