高精度恒温箱稳定性分析及鲁棒性改进
2022-10-10程东旭陈芝飞苏东赢马少华李瑞君
程东旭, 陈芝飞, 苏东赢, 马少华, 李瑞君
(1.河南中烟工业有限责任公司 技术中心,河南 郑州 450016; 2.合肥工业大学 仪器科学与光电工程学院,安徽 合肥 230009)
在微纳米测量领域,由温度波动引起的几何测量误差影响显著[1-3]。其中,由机械热变形引起的测量相对不确定度可以达到10 μm/℃[4]。研究表明,0.56 ℃的温度变化就会造成微纳米三坐标测量机工作台180 nm的结构热变形[5]。由此可见,高精密测量离不开精密的环境温度控制。此外,在激光干涉测量中,环境温度变化会造成激光中心波长偏移,带来测量误差。文献[6]研究了半导体激光器波长和温度的关系,采用具有集成检波器件的半导体激光器,设计了高精度波长稳定系统,稳定后波长稳定度优于2 pm。在激光准直测量中,温度变化会引起空气折射率波动,造成光束发生偏折,引起测量误差[7]。
为保障微纳米测量过程中测量环境的稳定性,文献[8]通过构建多层封闭式空间,为测量机所处的核心层提供高稳定的测量环境;文献[9]针对超精密加工环境控制需求,设置了一般控温区、精密控温区以及超精密控温区,通过多层温控环境的构建实现了超精密控温区(20 ± 0.05) ℃的控温精度。上述方法通过多层环境温度控制实现工作区温度稳定,结构设计较为复杂,而通过构建小型环境腔的方式,可以降低温度控制难度。文献[10]设计高精度标准铂电阻用空气恒温箱用于存放标准铂电阻,长期稳定性优于1 mK/月;文献[11]研究了一种外循环式恒温控制系统,箱体采用了水介质外循环式的分离结构,结构复杂,对安装人员要求较高;文献[12]研究了温湿度控制系统及其解耦模型,实现了温湿度同时控制。
文献[13-14]研究的基于自然对流原理的高精度恒温箱以半导体制冷片作为温控单元,采用PID控制算法,稳态控温精度最高可达±0.02 ℃,且结构简单、工作时无振动。然而,恒温箱使用要求箱体内外环境温差小于1 ℃,且需要定期调整PID控制器参数,以实现良好的控温精度。本文以已研制的恒温箱为研究对象,从系统稳定性入手,对系统自适应能力差的原因进行探究,并对控制系统进行优化,以提高系统的鲁棒性。
1 稳定性分析
1.1 恒温箱结构
恒温箱结构如图1所示。

图1 恒温箱结构
箱体采用亚克力板作为外框架材料,内壁粘贴真空隔热板以保障箱体的隔热性。箱体顶部安装有半导体制冷片作为温控执行器。工作时,测温仪34970A采集温度传感器PT100的电阻值,获得当前温度;控制器根据当前温度,调控恒流电源PSM6003的输出功率,驱动制冷片;制冷片在电流驱动下冷端开始制冷,对周围空气进行降温。此时,箱内产生纵向温度梯度,冷空气下降,热空气上升,形成自然对流,从而达到箱内控温的目的。
恒温箱结构参数如下:尺寸为900×900×1 000 mm;制冷片数量9;制冷片最大功率48 W(12 V/4 A);电源驱动功率180 W(60 V/3 A)。
1.2 温度扰动
恒温箱工作时,热源可以分为制冷片热辐射、环境热辐射、箱内器件热辐射3个部分。其中,环境热辐射和箱内器件热辐射以扰动形式存在于控制系统中。以环境热辐射为例,分析其对系统稳定性的影响。
环境热辐射对箱内温度有影响,计算公式为
θn=θb+θr(t)
(1)
其中:θn为恒温箱在环境热辐射下受到的温度扰动,由温度偏置θb及随机温度扰动θr2个部分组成;θb为当前环境温度水平,影响控制系统阶跃响应;θr为环境温度波动,影响系统的稳定性。器件热辐射对恒温箱造成的温度扰动同样可以用(1)式表示。综合环境热辐射与器件热辐射,最终得到恒温箱内总的温度扰动形式计算公式,即
θN=θB+θR(t)
(2)
其中:θB为综合温度扰动偏置;θR(t)为综合温度扰动随机分量。根据(2)式温度扰动存在形式,得到的系统传递过程如图2所示。由图2可知:① 温度偏置叠加至系统阶跃输入部分,影响系统初始工作条件;② 温度随机扰动叠加至系统输出部分,影响系统稳态精度。
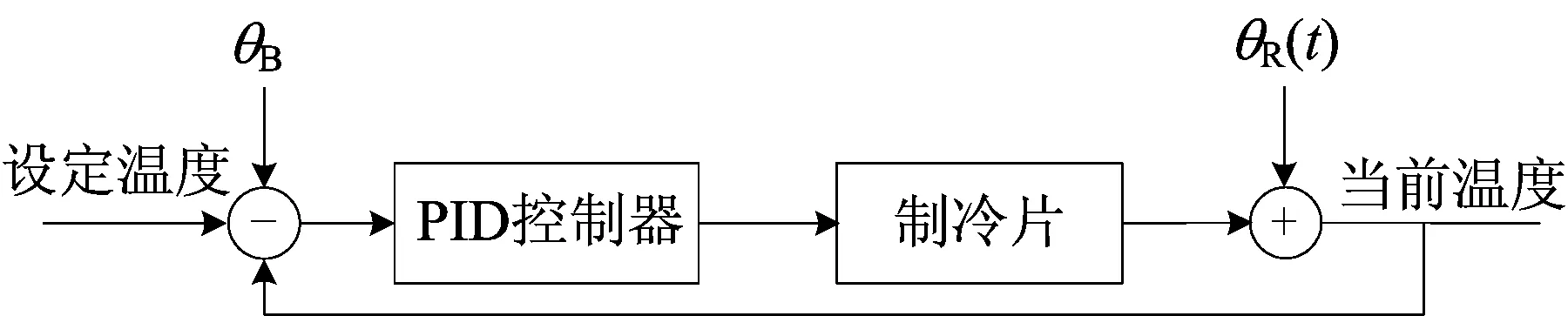
图2 系统传递框图
1.3 系统稳定性
除了温度扰动会影响控制系统响应,系统稳定性同样会制约控制系统性能。根据半导体制冷片实际物理传递过程,系统传递环节可以分为如下4个部分:① 电流驱动制冷片,制冷片制冷;② 制冷片与散热片热传导;③ 散热片与空气热传导;④ 空气自然对流传热。
求解系统的传递函数比较困难,而热传导过程通常具有稳定关系。因此,对半导体制冷片输入输出传递关系进行稳定性分析,一定程度上可以表征系统的稳定性。
制冷片输入电流与制冷量、制热量的关系[15]为:
(3)
其中:Qe为制冷量;Qh为制热量;Ic为输入电流;θc为制冷片冷端温度;θh为制冷片热端温度;Δθ为冷热端温差;α、R0、K为制冷片内参数。
由(3)式可知,制冷片冷端温度、冷热端温差、驱动电流共同决定制冷量,且三者相互制约。在理想情况下,认为制冷片工作时热端产生的热量全部通过风扇释放,热端温度保持不变,制冷功率由输入电流和冷端温度共同决定。实际工作时,由于热端散热不理想、环境热辐射等原因,热端温度随之发生变化。由此可见,制冷片输入输出间不仅存在非线性关系,且受多参数、多因素影响。因此很容易得出恒温箱非线性时变特性。
1.4 仿真测试
通过模型辨识对系统时变特性进行验证。根据前文分析可知,随着恒温箱工作时间增长,系统特性也将发生变化,分别取3个阶段对系统传递函数进行辨识:
(1) 关闭恒温箱,等待箱内温度稳定后,输入0.5 A恒定电流,获取箱内温度变化曲线后进行模型辨识。
(2) 箱内温度在恒定电流0.5 A作用下温度稳定后,调整输入电流至1.0 A,获取箱内温度变化曲线后进行模型辨识。
(3) 箱内温度在恒定电流1.0 A作用下温度稳定后,调整输入电流至1.5 A,采集箱内温度变化后进行模型辨识。
根据使用经验,恒温箱控温目标为20 ℃时,进入稳态后电流通常在1.0~1.5 A范围内。因此,这里选择0.5 A作为阶跃输入。辨识得到的系统模型表达式分别为:
(4)
(5)
(6)
(4)式、(5)式、(6)式辨识结果的拟合度分别为95%、94%、94%。(4)式比(5)式、(6)式多一个零点,具有显著的形式差异,(5)式、(6)式几乎相等。考虑模型辨识误差造成的系数差异,可以认为在第2阶段和第3阶段测试中,恒温箱具有稳定的系统模型。
在相同的PID参数下,进一步利用辨识得到的模型对PID控制效果进行仿真。这里只需对(4)式、(5)式进行仿真,前者为A组仿真,后者为B组仿真。仿真结果如图3所示。
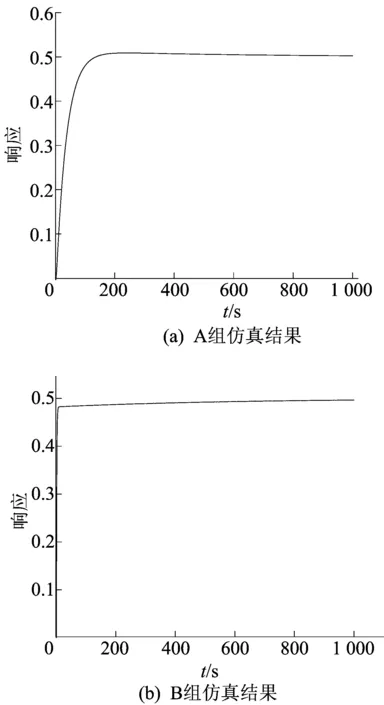
图3 PID控制仿真结果
从图3可以看出,(4)式的系统在阶跃激励下表现为衰减震荡,而(5)式为单调逼近,PID控制效果减弱。
综上所述,结合制冷片输入输出传递关系、恒温箱模型辨识结果及仿真测试,论证了恒温箱的非线性时变特性。在环境温度扰动、系统时变特性的影响下,传统PID难以获得稳定的控制效果,需要定期重新整定恒温箱PID系数,系统鲁棒性低。
2 模糊PID设计
2.1 模糊系统结构
模糊PID基于专家经验和模糊规则推理,能够根据系统状态自适应调整PID参数,不需要了解系统具体模型,在非线性时变系统中也能获得良好的控制效果。为了提高恒温箱自适应能力,设计了基于模糊PID的控制系统,如图4所示,以保证恒温箱稳态控制精度。
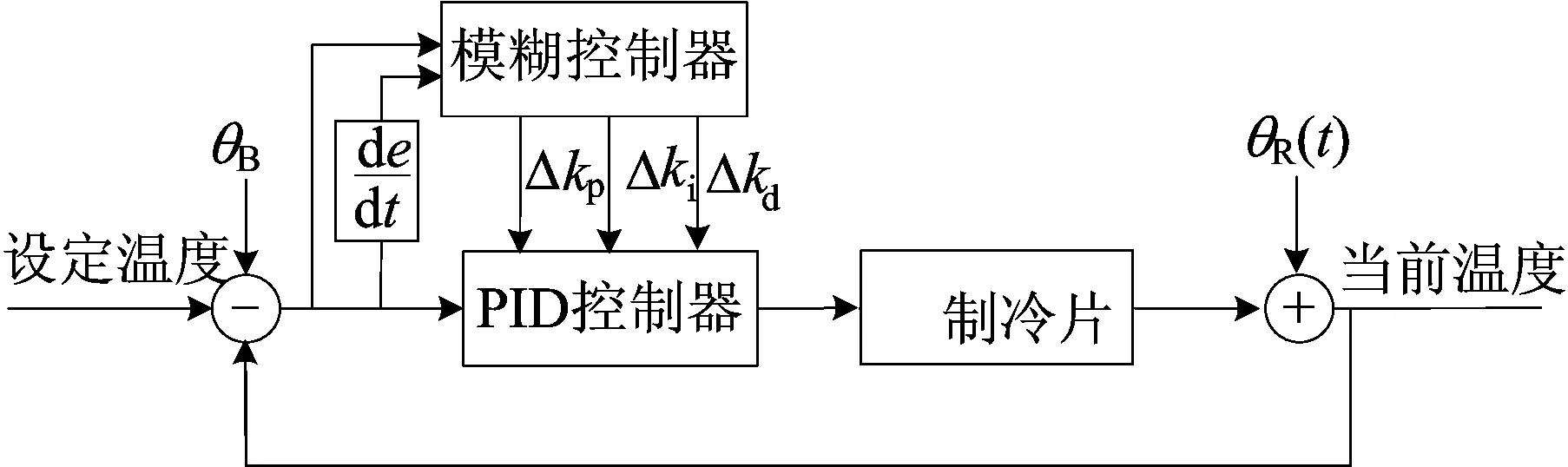
图4 基于模糊PID的恒温控制系统
模糊控制器输入参数为当前偏差e和偏差变化率ec,输出参数为比例参数Δkp、积分参数Δki、微分参数Δkd。经过调整的PID控制器参数计算公式为:
(7)
2.2 模糊化
模糊控制器输入输出论域、模糊语言见表1所列。
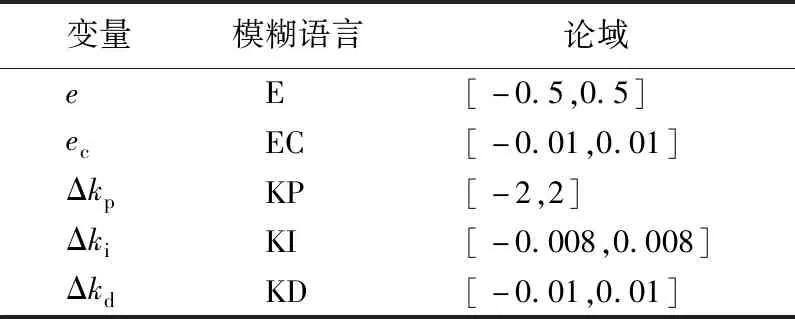
表1 模糊化设计
为了提高系统灵敏度,获得更好的稳态控制精度,对系统偏差输入进行了限定。
各模糊语言设定5个模糊子集,包括负大(NB)、负小(NS) 、零(ZO) 、正小(PS) 、正大(PB),隶属度函数选择三角型。为清晰展示各模糊子集及其隶属度函数形式,以归一化形式对模糊子集进行划分。对于任意模糊语言,其输入归一化映射表达式为:
y=x/X
(8)
其中:x为输入值;X为输入值最大范围;y为归一化值。
通过(8)式可以将在论域[-X,+X]之间的模糊语言映射在论域为[-1,+1]范围。各模糊语言归一化后的模糊子集及其隶属度函数关系如图5所示。
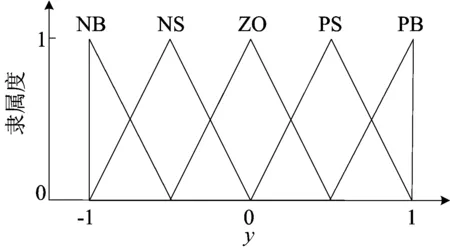
图5 隶属度函数
2.3 模糊规则设计
根据恒温箱控温调试经验和PID参数作用,建立了模糊规则。由恒温箱调试经验可知:
(1) 在|e|较大时,需要增加Kp值,以便系统快速响应,同时Ki值需要很小,防止积分饱和。
(2) 在|e|较小时,需要适当减少Kp值,防止系统震荡,同时增加Ki值,减少稳态误差。
(3)ec较大且为正时,代表系统迅速逼近目标值,Kd值需适当减少;ec较大且为负时,代表系统迅速远离目标值,Kd需适当增加进行补偿。
根据上述经验建立的模糊规则见表2所列。
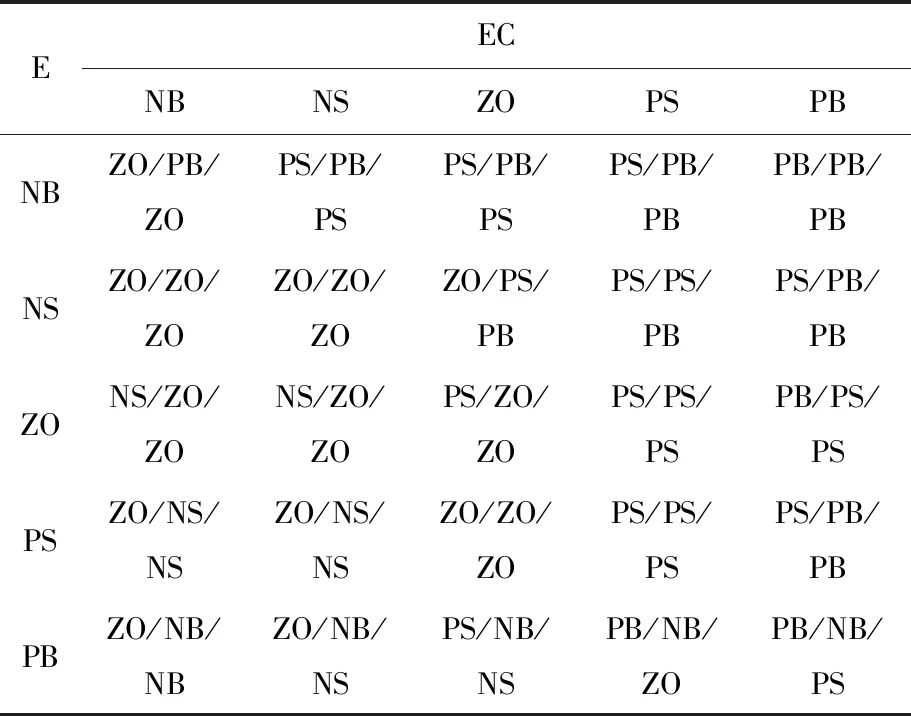
表2 Δkp、Δki、Δkd的模糊规则
选择IF-THEN语句进行模糊规则推理。在获得相应的输出模糊子集后,通过面积重心法进行去模糊化,获得模糊控制器输出。
3 实验验证
在之前的研究工作中,本团队设计了基于LabVIEW和MATLAB混合编程的高精度恒温箱控制软件。在此基础上,根据设计的模糊控制器对软件进一步优化,利用LabVIEW模糊设计工具完成基于模糊PID的高精度恒温控制软件。
为了验证模糊控制系统的有效性,随机设定恒温箱不同的状态,以验证系统自适应能力,包括变化系统阶跃幅值、变化系统模型参数。实验环境为可控温恒温室。具体实验步骤如下:
(1) 设定室温(23±0.5) ℃,关闭恒温箱,启动控制系统,验证控制系统最大温差适应能力。
(2) 设定室温(22±0.5) ℃,关闭恒温箱,启动控制系统,此时控制系统在当前环境状态下具有最大的阶跃输入,系统模型用(4)式表示。
(3) 设定室温(22±0.5) ℃,关闭恒温箱,以恒定电流值0.5 A驱动制冷片,在箱内温度稳定后启动控制程序,此时控制系统阶跃输入和模型参数发生变化,系统模型用(5)式表示。
实验结果见表3所列。每组测试时长10 h,计算稳态波动时,取最后2 h数据进行计算。第2组测量结果如图6所示。
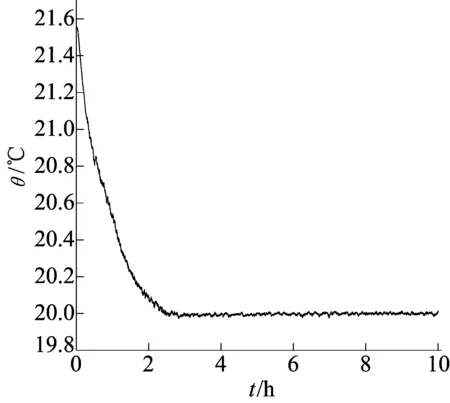
图6 室温21.549 ℃下恒温箱控温结果
由表3中1组、2组实验可知:优化后的温控系统能够在不同环境温度下保持良好的稳态控温精度;2组、3组实验证明,在系统时变特性下,温控系统也能获得良好的控制效果,鲁棒性增强。
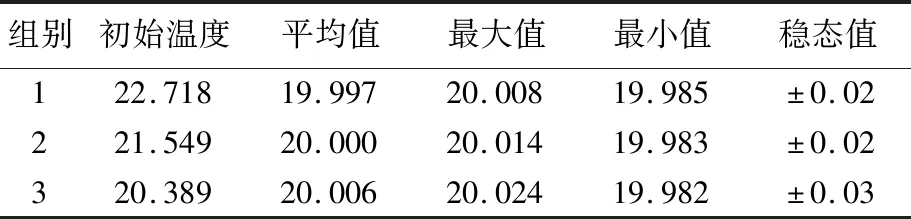
表3 实验结果 单位:℃
4 结 论
本文针对基于自然对流原理的微纳米三坐标测量机用高精度恒温箱鲁棒性差的问题,研究了温度扰动及系统稳定性对恒温箱性能的影响,并根据系统辨识结果建立仿真模型,验证结论的有效性;为增强恒温箱自适应能力,保障稳态控温精度,采用模糊PID优化了恒温箱控制系统软件,并设定恒温箱不同的状态进行效果验证。
实验结果表明,优化后的控制系统具有良好的自适应能力,环境温差适应能力由1 ℃提升至3 ℃,且能很好地抵抗系统时变特性,稳态控制精度优于±0.03 ℃,系统鲁棒性强。
