“‘平行四边形’复习课”教学实录及反思

■谢射红

平行四边形是初中“图形与几何”内容中的最基本的图形之一。研究平行四边形有利于进一步培养学生理性的几何直观和空间想象力，感悟数学论证的严密性、逻辑性。本节课既是三角形相关知识的延伸和拓展，也是后续复习“图形的性质”“图形变化”“图形与坐标”的基础，起着承上启下的作用，对发展初中生的推理能力等有着举足轻重的作用。

一、学情分析

九年级学生虽然对平行四边形有了一定认识，但是仍存在对平行四边形的性质与判定的混淆，对平行四边形在几何中的地位与作用缺乏整体认识，对平行四边形与其他知识之间的联系缺乏深度思考，知识碎片化严重。

二、目标分析

通过系统回顾平行四边形的定义、性质及判定，建构知识网络，积累运用平行四边形解决问题的活动经验，体会分类讨论、数形结合等常见数学思想，促进几何直观、空间观念、推理能力、数学核心素养的提升。

三、教学实录

师：同学们，我们前面已经复习了三角形的相关知识，现在你能否将△ABC通过某种图形变换得到一个四边形？（图略）

生1：可以将△ABC沿边BC翻折。（图略）

生2：可以绕BC边中点O旋转180°。（图略）

【设计意图】从三角形到四边形，由中心对称的性质得到平行四边形的边、角、对角线的性质，可以为后面知识的梳理找到一个生长点。

活动一：建构知识体系。

师：你能否在平面上找一点D，使得四边形ABCD为平行四边形？（如图1）

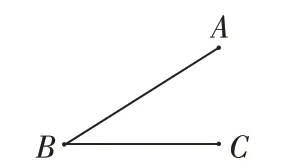
图1

生3：可以过点A画BC的平行线，过点C画AB的平行线，两条平行线的交点即为点D。（根据平行四边形定义）

生4：可以过点A作BC的平行线，再以点A为圆心，BC长为半径画弧交BC的平行线即为点D。（根据平行四边形判定定理1）

生5：可以以点A为圆心，BC长为半径画弧，再以点C为圆心，AB长为半径画弧，两弧交点即为点D。（根据平行四边形判定定理2）

生6：可以连接AC，取AC的中点O，再以点O为圆心，OB长为半径画弧，与BO的延长线的交点即为点D。（根据平行四边形判定定理3）

【设计意图】教师摒弃了传统复习课模式，选择以任务为载体、问题为驱动，激发学生思维，引导学生对平行四边形的内容体系进行自主建构。

师：在▱ABCD中，AB=4，∠ABC=30°，AC⊥BC。你能求出哪些结论？

生7：利用直角三角形的边角关系，可以求出平行四边形所有的边长。

生8：可以求出对角线的长。

生9：可以求出所有的角。

【设计意图】教师通过设置开放性问题，引导学生灵活运用平行四边形知识，从而提高学生的分析和识图能力。

活动二：关联考点。

师：在△ABC中，∠ACB=90°，你能否在平面直角坐标系上找一点D，使得以A、B、C、D为顶点的四边形为平行四边形，情况又如何？

生10：除了以AC为对角线外，还可以以AB、BC为对角线。

【设计意图】为了提高学生的综合运用能力，教师将图形放在平面直角坐标系这个背景中，是基于对整个初中阶段所学知识的考查。这是呼应前面的画图，也利于分解难点，达到发展高阶思维的目的。同时，也是巩固复习已知三个顶点，确定第四个顶点的问题的一般思维方式，体现分类讨论思想方法。

活动三：生长探究能力。

师：平行四边形是从边、角、对角线的三个角度进行研究的，类比平行四边形的研究方法，大家研究一下筝形（图略）。

生11：有两组邻边相等的四边形叫作筝形。

生12：有一条对角线垂直平分另一条对角线的四边形叫作筝形。

生13：以一条对角线所在直线为对称轴的四边形叫作筝形。

师：抓住图形的特征来定义都是可以的，第三种更是抓住了图形的生成过程，我们不妨取第三种作为定义。

师：筝形有哪些性质呢？

生齐：有两组邻边相等；有一组对角相等；一条对角线垂直平分另一条对角线……

师：如何探究筝形的判定呢？

生（齐）：可以根据它的性质，从边、角、对角线层面反推等。

……

【设计意图】教师通过类比平行四边形研究新图形，培养了学生对所学知识的提取、运用、迁移能力，也回应了“为什么学”的基本目标，让探究的方法自然生长，促进学生数学核心素养的提升，让学生学会用数学的眼光去观察现实世界，用数学的思维去思考现实世界，用数学的语言去表达现实世界。

四、教学反思

中考复习是学生对初中阶段学习内容的回顾与梳理，也是对所学知识的查漏补缺，更是形成知识体系，发展数学核心素养的过程。

复习课中我们要整体建构知识体系，关联考点，提升探究能力，尤其在当前的“双减”背景下，课堂要符合减负增效的要求。本节课从以下两个方面反思：

一是注重内容整体建构。本节课在梳理知识时，改变了传统的以教师讲为主的课堂，采用了以任务为载体、问题为驱动的课堂，激发学生思维，引导学生对平行四边形的知识体系进行整体建构，形成知识网络。同时，学生用联系的、变化的观点认识初中几何知识，并综合在一起提出问题、解决问题，有助于培养用发展的眼光来观察问题。

二是体现数学素养价值。在本节课中，学生运用平行四边形性质解题，有利于推理能力的发展。类比探索过程，从平行四边形的定义、性质、判定出发，研究新的四边形。在知识转化为能力的过程中，学生通过感悟和体验，利用新的问题情境解决问题，自身能力得到了巩固和强化。最后，教师通过整合与优化新的能力结构，使学生的数学探究能力得到了发展。对于新定义的问题，教师将常见的知识点赋予新的问题情境，学生通过探索、推理、联想、类比平行四边形的方法，真正学会研究问题的一般路径。