6061-T6 铝合金动态拉伸本构关系及失效行为*

周 伦，苏兴亚，敬 霖，邓贵德，赵隆茂

（1. 西南交通大学牵引动力国家重点实验室，四川 成都 610031；2. 四川航空工业川西机器有限责任公司，四川 雅安 625000；3. 中国特种设备检测研究院，北京100029；4. 太原理工大学应用力学研究所，山西 太原 030024）

金属材料通常具有应变率敏感性，在遭受爆炸、冲击、碰撞等动态载荷作用时其力学响应特征与准静态情况下的有所不同，并往往伴随着塑性变形和断裂破坏。因此，开展可描述金属材料在大应变和动态载荷下本构关系及失效准则的研究，对于防护结构的设计和优化具有重要意义。目前研究者们提出了多种本构模型来表征材料的动态力学行为，常见的有Cowper-Symonds (C-S)模型、Johnson-Cook(J-C)模型、Zirilli-Armstrong (Z-A)模型等，J-C 模型因具有形式简洁、物理意义明确、参数易获得等优点被广泛使用。此外，J-C 失效模型同时考虑了应力三轴度、应变率和温度对材料力学性能的影响，能够较好地预测率温耦合下材料的断裂失效行为，在冲击碰撞问题的研究中占有重要地位，其中，应力三轴度定义为静水压力与Mises 等效应力的比值，通常用来表示材料的应力状态。学者们研究了Q235 钢、7A04 铝合金、钛合金等金属或合金缺口试件的拉伸力学性能，得到了应力三轴度与断裂应变之间的关系，并建立了可准确描述其断裂失效行为的J-C 失效模型。

6061-T6 铝合金具有良好的焊接性、强耐腐蚀性、易于加工等特点，被广泛应用于航空航天、交通运输和国防工程等领域。Lee 等和Zhu 等对6061-T6 铝合金的压缩及拉伸力学性能开展了研究，发现该材料具有明显的应变率强化效应。随着应变率的提高，6061-T6 铝合金的压缩屈服应力、流动应力和应变率敏感性指数逐渐增大，而加工硬化率则表现出降低的趋势；应变率对材料的晶粒也会产生一定影响，在高应变率范围内材料晶粒尺寸有所增大而晶粒形状变细。Odeshi 等研究发现，高应变率下绝热剪切带的出现是导致材料压缩塑性变形和破坏的根本原因。Zhu 等对拉伸断口形貌的研究发现，静、动态拉伸载荷下6061-T6 铝合金均呈现出韧性断裂特征。在本构模型方面，Acharya 等基于实验结果建立了材料具有物理意义的动态本构模型，并对预测结果进行了验证。可以看出，目前针对6061-T6 铝合金力学响应的研究主要集中在准静态和高应变率加载，对中应变率范围内力学行为的研究比较匮乏。然而，6061-T6 铝合金作为民用工程结构材料时，其动态冲击服役过程常处于中应变率加载场景，如汽车/列车碰撞、冲压成型、物体坠落等。

因此，本文中，开展6061-T6 铝合金在0.001～100 s应变率范围内的拉伸力学性能实验，讨论其力学响应特征和应变率敏感性，分析应变率对材料塑性流动的影响；基于完整试件的拉伸实验结果对J-C本构模型进行修正，结合缺口试件的拉伸实验结果和数值模拟得到修正J-C 失效模型参数值，并对修正J-C 模型的准确性和适用性进行验证。

1 J-C 模型

1.1 J-C 本构模型

合适的本构模型是准确预测外载荷作用下材料力学响应的关键。J-C 本构模型作为典型的经验型本构模型，综合考虑了应变、应变率和温度对塑性流动的影响，可以准确描述材料的应变硬化特征和率-温耦合效应，能够较好地预测大变形、高应变率和高温下材料的力学响应：

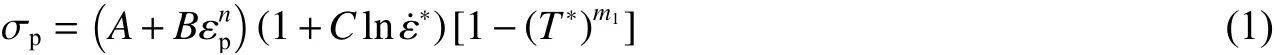
1.2 J-C 失效模型

金属材料在大变形过程中常出现断裂失效，而断裂失效与其应力状态（应力三轴度、Lode 角等）密切相关，且通常表现出一定的应变率敏感性和温度依赖性。J-C 失效模型同时考虑了应变率、温度和应力三轴度对材料断裂失效的影响，并基于累积损伤准则确定了损伤量的表达式：

2 6061-T6 铝合金动态本构关系

2.1 静动态拉伸力学性能

实验材料为6061-T6 铝合金，是由6061 铝合金进行固溶热处理后经人工时效制备而成，其化学成分如表1 所示。采用线切割方法在铝锭上均匀取样，为避免尺寸效应对实验结果的影响，静动态拉伸实验均采用厚度为2 mm、标距段宽度为4 mm 的片状试件，如图1 所示。利用HMH-206 型高速材料试验机，分别开展0.001、0.1、1、10 和100 s等5 种应变率下材料的拉伸力学性能实验。为确保实验结果的可靠性，每种应变率工况均开展3 次有效重复性实验，选择最接近平均值的应力-应变响应曲线进行力学性能分析。

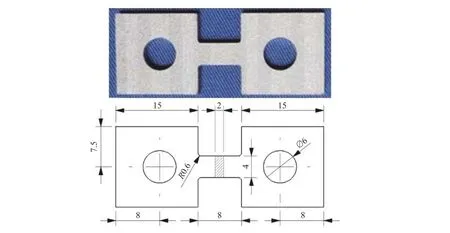
图1 拉伸试件及其几何尺寸（单位：mm）Fig. 1 Picture and dimension of the tensile specimens (unit: mm)

表1 6061-T6 铝合金的化学成分（质量分数）Table 1 Chemical composition of 6061-T6 aluminum alloy (mass fraction)%

不同应变率下6061-T6 铝合金真实应力σ与真实应变ε之间的关系如图2(a)所示，材料的应力-应变曲线均表现出双线性弹塑性特征，没有出现明显的屈服平台。在拉伸初始阶段，应力随应变的增大呈线性升高；当材料进入塑性流动阶段时，应力随应变的增大有所升高但升速明显放缓，材料出现应变硬化现象。图2(b)给出了真实应变为0.05、0.06、0.07 和0.08 时6061-T6 铝合金流动应力与应变率之间的关系。由图可知，相同应变下流动应力随应变率的升高明显增大，材料表现出应变率强化效应。这是因为在拉伸过程中材料内部会产生大量高密度位错盘结和位错胞，位错密度随应变率的升高而增大，此时克服位错运动所需要的外力就越大。材料的变形靠其内部的位错滑移来实现，而位错滑移线在晶格内移时会受到晶格内间隙原子等缺陷的阻碍和约束，导致在较高应变率下位错滑移线的移动速度滞后于载荷的增大速度，使得滑移线很难以较快速度贯穿整个晶粒，宏观上表现为相同应变下流动应力随应变率的升高而增大。

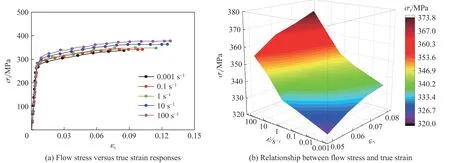
图2 不同应变率下6061-T6 铝合金的拉伸实验结果Fig. 2 Tensile test results of 6061-T6 aluminum alloy at different strain rates

在给定应变ε 和温度下，可以用应变率敏感性指数来描述应变率对材料力学性能的影响，其表达式为：

式中： ε˙和ε ˙分别为动态和准静态应变率，σ和σ分别为动态和准静态应变率对应的流动应力。该方法假定材料的对数流动应力差值与对数应变率差值线性相关，两者的比值即为应变率敏感性指数。从图2(b)可以看出，随着应变率的升高，不同应变下6061-T6 铝合金的流动应力变化趋势有所不同。因此，利用给定应变下的流动应力进行计算无法反映材料真实应变率效应。为了准确得到6061-T6 铝合金的应变率敏感性，图3 给出了不同应变和不同应变率下材料的应变率敏感性指数。可以看出，不同应变下材料的应变率敏感性指数随应变率的升高逐渐增大，而动态压缩载荷下该材料也出现相同的现象。

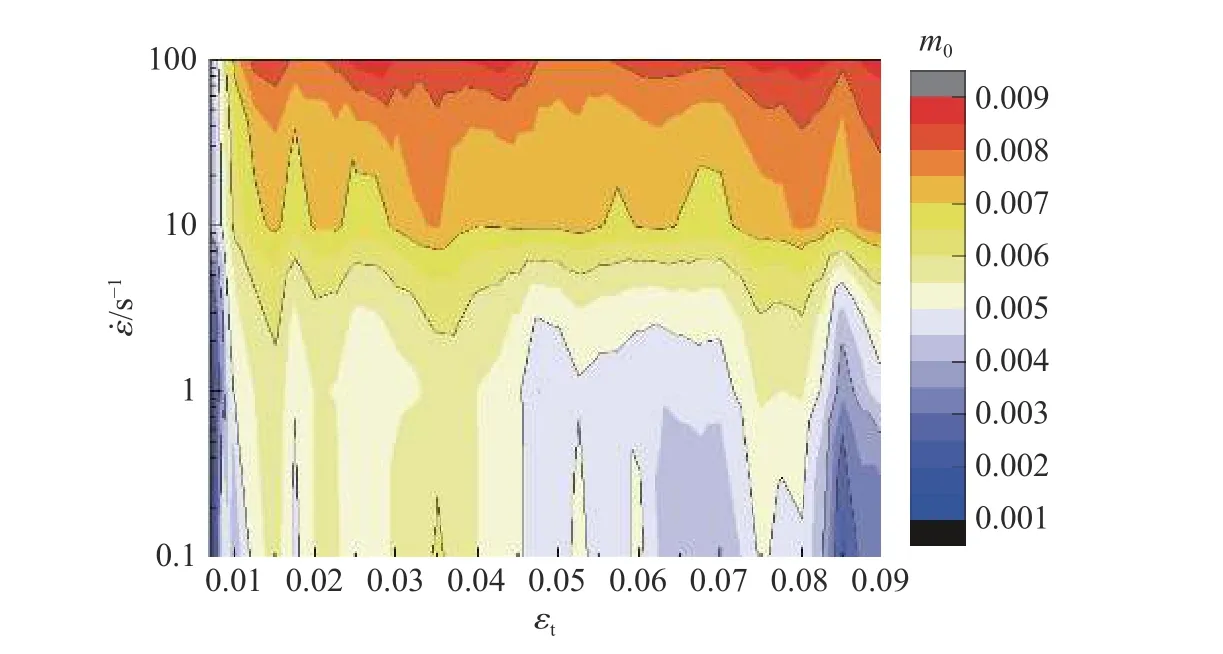
图3 不同应变下应变率敏感性指数与应变率之间的关系Fig. 3 Relationship between strain rate sensitivity index and strain rate at different strains

2.2 修正的J-C 本构模型

根据图2(a)中6061-T6 铝合金的拉伸实验结果，通过拟合可得到J-C 本构模型参数值。具体步骤为：首先，根据参考应变率（0.001 s）下材料的屈服强度确定= 275.96 MPa；然后，利用最小二乘法对该应变率下的应力-应变响应进行拟合，得到= 288.39 MPa 和= 0.59；最后，对0.1、1、10 和100 s应变率下材料的屈服强度进行拟合，得到= 0.006 4。由于应力-应变曲线中没有出现明显的屈服平台，这里取真实塑性应变0.2%对应的应力作为材料的屈服强度。图4(a)对比了模型预测和实验结果，可以看出，在较低应变率下两者吻合较好，当应变率为100 s时，该模型会过低估计材料的流动应力。这是因为J-C 本构模型中应变率敏感性系数为恒定值，而该参数反映了材料对应变率的敏感程度，从图4(a)对比结果可知，在越高的应变率下6061-T6 铝合金的应变率效应越明显。把J-C 本构模型中的修正为 l n ε˙的一次函数，得到：

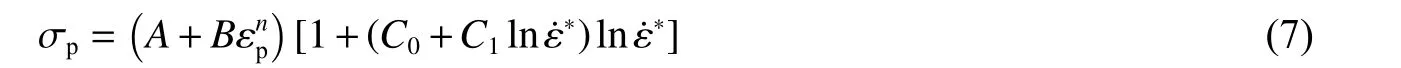
利用最小二乘法对动态拉伸实验结果进行拟合，得到6061-T6 铝合金修正的J-C 本构模型参数值：= 275.96 MPa，= 288.39 MPa，= 0.59，= -0.002 23，= 0.001 05。图4(b)给出了模型预测和实验结果对比，可知修正的J-C 本构模型能够表征动态拉伸时6061-T6 铝合金的塑性流动行为。

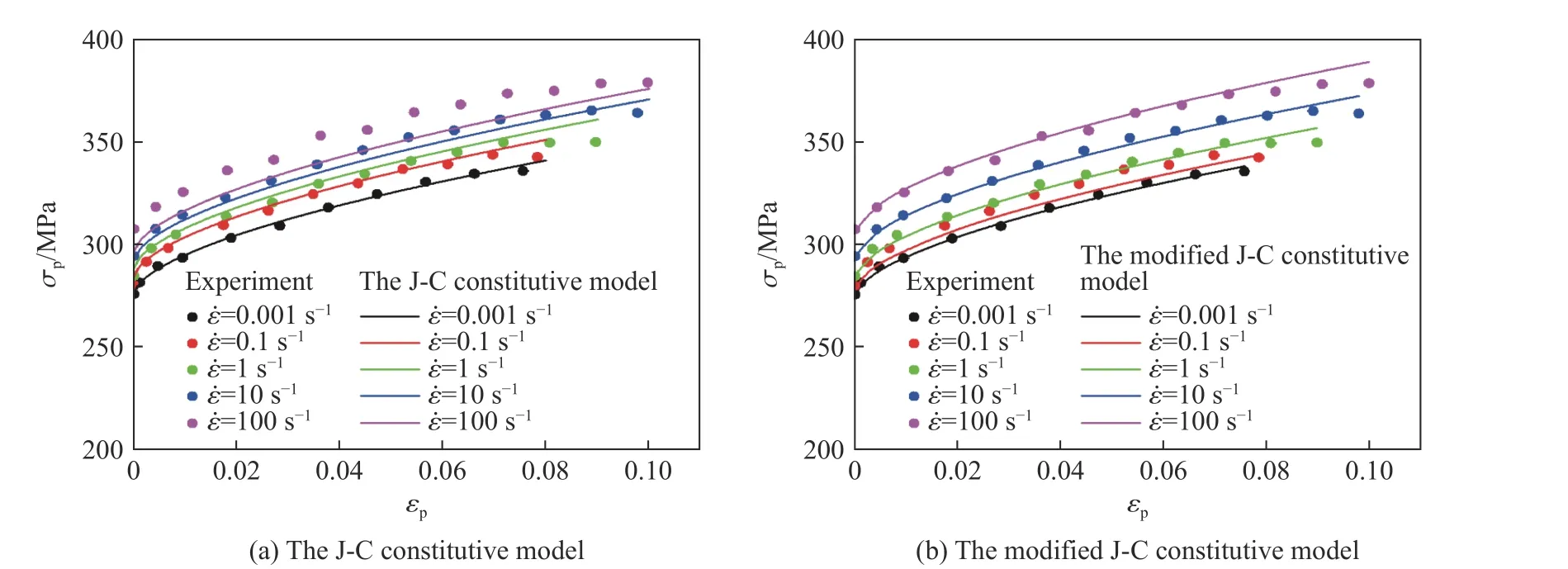
图4 模型预测与实验结果对比Fig. 4 Comparison of predictions by the models with experimental results

3 6061-T6 铝合金失效参数

3.1 失效参数的测定

对于J-C 失效模型，可靠的模型参数是准确预测材料断裂应变的前提。由式(5)可知，为了获得模型参数值，首先需要确定应力三轴度和应变率分别与断裂应变之间的关系，然后拟合得到参数～。通常情况下，可通过缺口试件的拉伸实验或有限元模拟来研究J-C 失效模型参数。针对图1 所示6061-T6铝合金试件，利用HMH-206 型高速材料试验机开展3 种不同缺口半径(1、2 和3 mm)试件的轴向拉伸实验，并结合ABAQUS 有限元分析软件，来考察应力三轴度对断裂应变的影响。图5(a)为缺口试件，不同缺口试件最小截面的宽度均为2 mm，拉伸速率为0.08 mm/s。每种类型缺口试件均开展3 次实验，不同类型缺口试件3 次实验结果的重复性较好，这里选择最接近平均值的载荷-位移曲线进行数值模拟，如图5(b)所示。可以看出，大半径缺口试件具有较强的抗拉能力，而断裂时刻该试件的拉伸变形量较小。

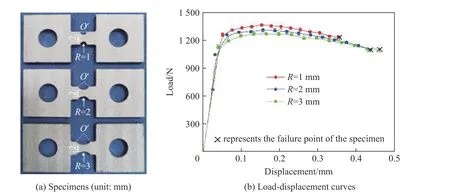
图5 6061-T6 铝合金缺口试件和拉伸载荷-位移曲线Fig. 5 Notched 6061-T6 aluminum alloy specimens and their tensile load-displacement curves

3.1.1 确定断裂应变和应力三轴度

在拉伸载荷作用下，试件的断裂应变ε可根据其断口面积计算得到：

式中：为试件最小截面面积，为断口面积。

由于试件的拉伸断口形状复杂，通常很难准确测得断口面积，可借助数值模拟技术获得断裂应变。利用数值模拟方法获得缺口试件断裂应变的方法主要包括：(1)提取断裂时刻最小截面中心点等效塑性应变作为断裂应变；(2)选择断裂时刻最小截面所有单元的平均等效塑性应变作为断裂应变。由于缺口试件某点的损伤达到临界值与试件断裂发生在拉伸过程中的不同时刻，通常情况下两者对应的应变不同，某点处失效无法真实反映试件的整体断裂行为。因此，取断裂时刻最小截面所有单元的平均等效塑性应变近似作为试件的断裂应变。

试件的应力三轴度与缺口大小密切相关，Bridgman 等在早期给出了棒状缺口试件应力三轴度的计算方法：

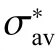
式中：为断裂截面面积，d为断裂截面上的面积微元。

3.1.2 应力三轴度对断裂应变的影响

利用ABAQUS 软件，分别建立3 种缺口半径（1、2 和3 mm）6061-T6 铝合金试件的有限元模型，来研究拉伸过程中试件的应力三轴度和断裂应变。采用六面体单元对模型进行划分，其中夹持端网格尺寸为0.2 mm × 0.2 mm，缺口区域网格细化为0.1 mm × 0.1 mm。模型一端施加固定边界条件，另一端沿轴向施加0.08 mm/s 的恒定拉伸速度。金属试件在拉伸过程中通常会产生颈缩，导致颈缩处材料产生非均匀变形并处于多轴应力状态，此时其应力-应变关系很难准确获得。为了准确模拟6061-T6 铝合金缺口试件的拉伸力学行为，采用有限元迭代计算修正的方法模拟缺口试件的拉伸过程。具体步骤为：首先以图2(a)中准静态应力-应变响应结果作为材料参数输入到模型中进行数值模拟，接着把模拟得到的载荷-位移曲线与图5(b)中实验结果进行对比并得到两者的相对误差，然后通过乘以相应系数来调整应力-应变曲线中的应力幅值，再把调整后的应力-应变曲线输入到模型中进行数值模拟，直至模拟得到的结果逼近实验数据为止，如图6 所示。

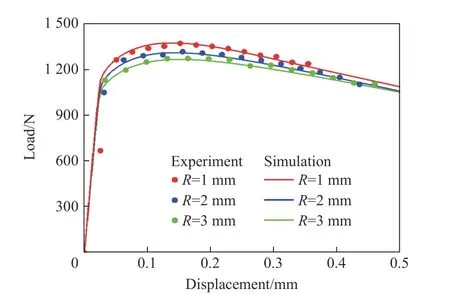
图6 实验和数值模拟得到的缺口试件载荷-位移曲线Fig. 6 Load-displacement curves of the notched specimens obtained by experiments and simulations

图7 为6061-T6 铝合金缺口试件Mises 应力云图和最小截面处应力三轴度的分布情况，其中图7(b)、(d)、(f)中坐标原点对应试件最小截面的中心点，横坐标和纵坐标分别表示沿宽度（方向）和厚度（方向）方向与中心点的距离。可以看出，在拉伸过程中不同缺口半径试件的应力关于最小截面呈对称分布。由于缺口效应的存在，试件中心区域产生了应力集中，且应力随着与最小截面距离的增大而减小。此外，试件最小横截面处的应力三轴度沿宽度和厚度方向关于中心线呈对称分布，且随着与中心点距离的增大而减小，其中最大应力三轴度出现在截面中心处，说明拉伸过程中最小截面中心区域的应力状态比边缘区域更复杂。图8 给出了缺口试件最小截面中心点处应力三轴度 σ随等效塑性应变ε的变化情况，可以看出，拉伸过程中最大应力三轴度随等效塑性应变的累积呈增大趋势。在相同等效塑性应变下，应力三轴度随缺口半径的减小而增大，这是因为缺口效应随着缺口半径的减小逐渐增强，导致小半径缺口试件的应力集中效应更明显。

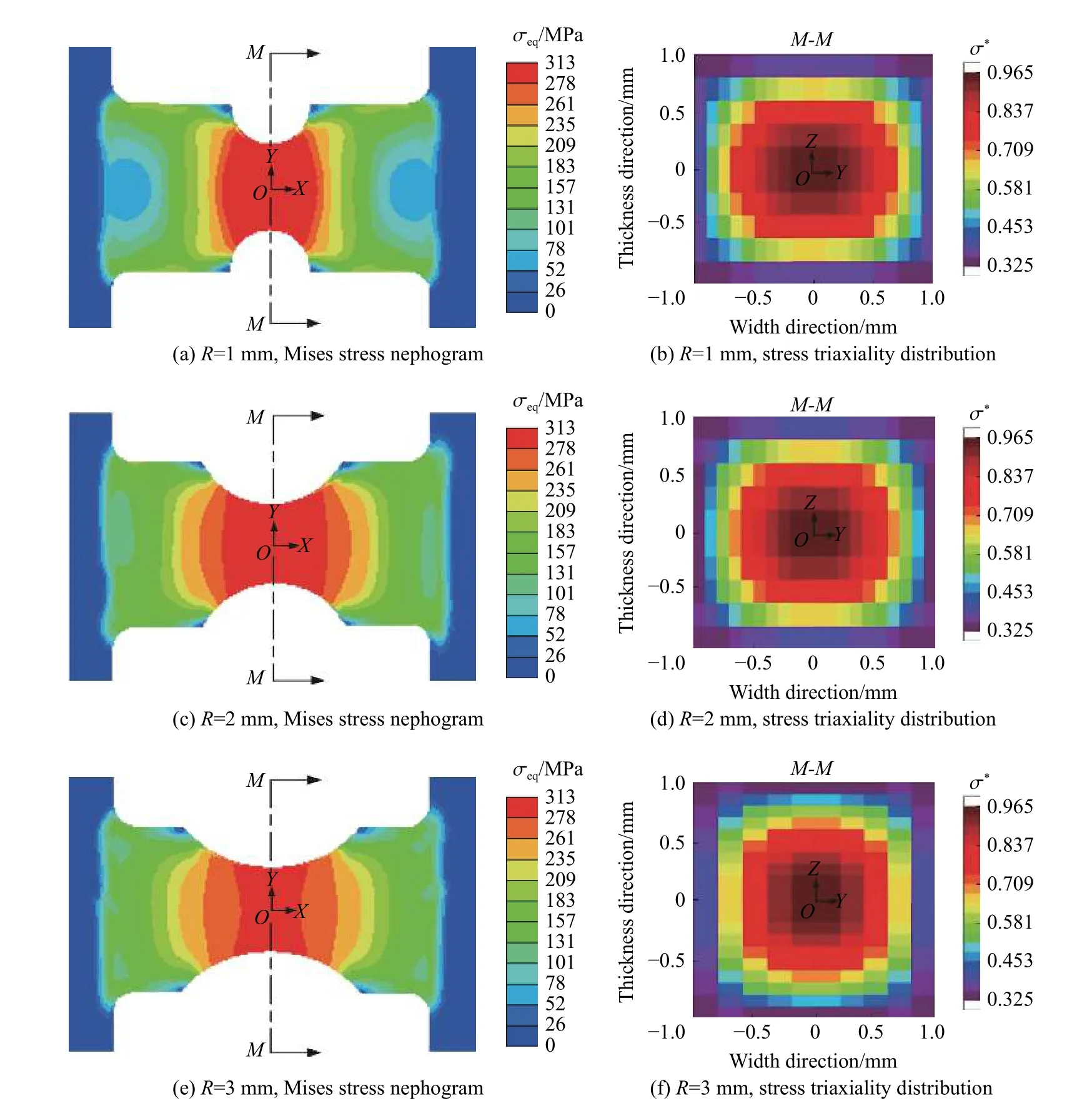
图7 不同缺口半径试件的Mises 应力云图和应力三轴度分布Fig. 7 Mises stress nephograms and stress triaxiality distributions for notched specimens with different radii

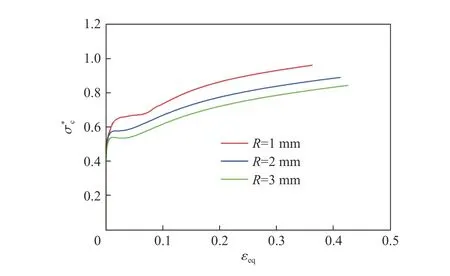
图8 缺口试件最小截面中心点应力三轴度与等效塑性应变的关系Fig. 8 Relationship between stress triaxiality at the center points of the minimum cross-sections of notched specimens and equivalent plastic strain

由于实验过程中无法得到6061-T6 铝合金缺口试件的应力三轴度，因此通过提取相同拉伸速度（0.08 mm/s）下完整试件和3 种不同缺口半径（1、2 和3 mm）试件的有限元模拟结果，来研究断裂应变与应力三轴度之间的关系。拉伸速度为0.08 mm/s 时，完整试件的加载应变率为0.01 s，而因缺口试件拉伸过程中变形不均匀，无法直接获得其加载应变率。这里通过提取缺口试件失效前最小截面单元不同时刻的轴向平均应变，并对应变-时程响应进行线性拟合得到缺口试件的最大应变率（即斜率）。3 种不同缺口半径（1、2 和3 mm）试件的最高应变率分别为0.052、0.059 和0.051 s，结合图2(a)中拉伸应力-应变响应结果可知，在此应变率区间内，应变率对试件应力-应变响应的影响可忽略不计。也就是说，基于拉伸速度0.08 mm/s 下完整试件和缺口试件的模拟结果来研究断裂应变与应力三轴度之间的关系是可行的。图9(a)给出了不同应力三轴度下试件的断裂应变，可以看出，断裂应变随应力三轴度的增大而减小，且减小速率呈上升趋势。在参考应变率下，采用最小二乘法并根据式(5)对模拟结果进行拟合，可得到失效参数= 0.362，= -4.57×10和= 17.434。

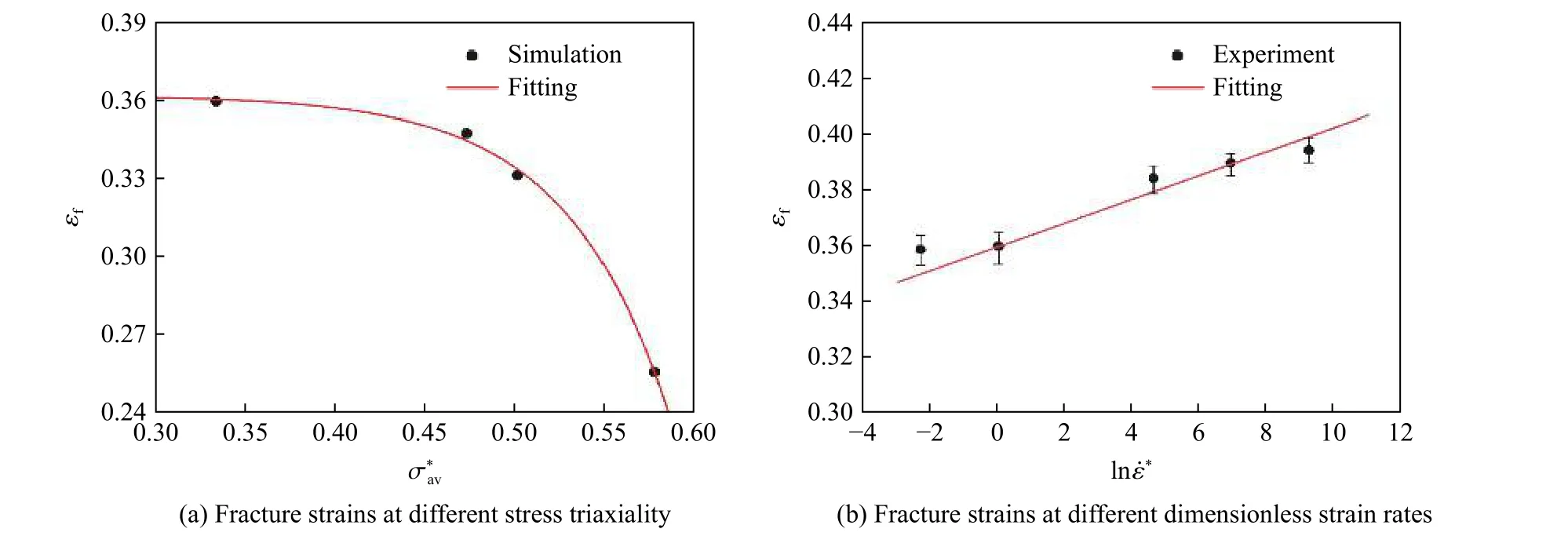
图9 断裂应变与应力三轴度和无量纲对数应变率的关系Fig. 9 Relationships of fracture strain with stress triaxiality and dimensionless strain rate

3.1.3 应变率对断裂应变的影响

由式(5)可知，为了得到材料参数，需获得断裂应变与无量纲应变率 ε˙之间的关系。根据图2(a)中不同应变率下6061-T6 铝合金完整试件的拉伸实验结果，以0.001 s为参考应变率，得到断裂应变与对数无量纲应变率 ε˙之间的关系如图9(b)所示。其中断裂应变ε通过测量试件截面面积和断口面积，并根据式(8)计算获得。由图9(b)可知，断裂应变随对数无量纲应变率的升高近似呈线性增大，对实验结果进行拟合得到J-C 失效模型参数= 0.011 2。

3.2 失效模型验证

为了验证J-C 本构模型和失效模型的准确性与适用性，在图1 所示6061-T6 铝合金拉伸试件中间位置处截去直径为2 mm 的圆孔制作模型验证试件，如图10 所示。由于圆孔的存在，试件测试段已不满足均匀性假设，在拉伸过程中会引入结构响应，从而形成复杂应力状态。采用HMH-206 型高速材料试验机开展加载速度分别为0.8、8 和80 mm/s 的轴向拉伸实验，并利用ABAQUS 软件开展相应的有限元模拟，把确定的J-C 本构模型和失效模型参数作为模拟参数进行输入。不同拉伸速度下实验和仿真得到的载荷-位移曲线如图11 所示，可以看出，实验数据和仿真结果整体吻合较好，表明本文中建立的J-C 模型能够预测复杂应力状态下6061-T6 铝合金的拉伸力学响应与断裂失效行为。

图10 6061-T6 铝合金模型验证试件Fig. 10 The 6061-T6 aluminum alloy specimen used for model verification

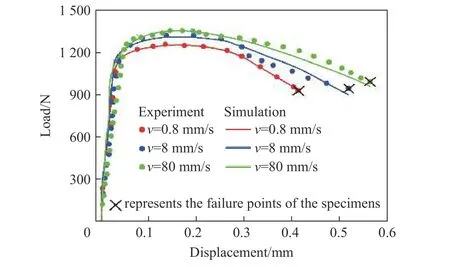
图11 不同加载速度下实验和模拟得到的载荷-位移曲线对比Fig. 11 Comparison of the load-displacement curves obtained by experiments and simulations at different load velocities

4 结 论

采用HMH-206 型高速材料试验机开展了6061-T6 铝合金的静、动态拉伸力学性能实验，讨论了其应力-应变响应特征和应变率敏感性，基于实验结果对J-C 本构模型进行了修正，利用实验和数值模拟相结合的方法建立了6061-T6 铝合金的J-C 失效模型，并对模型的准确性和适用性进行了验证，获得如下主要结论。

(1)静、动态拉伸载荷下，6061-T6 铝合金表现出明显的应变硬化特征和应变率敏感性。在塑性变形初始阶段，材料的应变硬化能力较强，随着材料塑性变形的加剧，其应变硬化能力逐渐减弱。在考察的应变率范围内，6061-T6 铝合金具有应变率强化效应，其流动应力随应变率的升高而增大，且高应变率下流动应力增量大于低应变率时的结果。

(2)拉伸过程中，缺口试件最小横截面处应力三轴度沿宽度和厚度方向关于中心线呈对称分布，最大应力三轴度出现在中心点处。随着等效塑性应变的增大，缺口试件最小截面中心点处的应力三轴度逐渐增大，且小半径缺口试件具有更大的应力三轴度。

(3)圆孔试件的验证结果表明，本文中修正的J-C 本构模型和失效模型可以预测复杂应力状态下6061-T6 铝合金的拉伸力学响应和断裂失效行为。