基于稀疏贝叶斯的阵列幅相和互耦误差联合校正方法

王鼎，高卫港，吴志东

（信息工程大学信息系统工程学院，河南 郑州 450001）

0 引言

阵列信号处理技术自面世以来，在雷达[1]、通信[2]、水声[3]、医学[4]等领域得到了广泛的应用。同时，随着阵列处理理论的不断完善发展，空间谱估计技术因其在远距离探测、低截获信号处理等方面的优势，受到了国内外学者的关注。

纵观空间谱估计技术的整个发展历程，从最开始的传统空间谱估计，即经典傅式谱分析在空域上的直接推广，这种方法因受限于阵列孔径无法突破“瑞利限”[5]，到后来的现代空间谱估计技术，其中最具代表性的便是以子空间技术为基础的多重信号分类（MUSIC,multi signal classification）算法[6]。与传统空间谱估计技术相比，MUSIC 算法的估计精度和角度分辨率都达到了新的高度。但是，随着子空间算法理论的不断发展，此类算法的局限性也逐渐暴露出来，对阵列输出协方差矩阵以及信号/噪声子空间的准确度有高度依赖性导致子空间算法在低信噪比及小快拍情况下效果并不理想。此外，在发展过程中，还出现了极大似然类测向方法[7]，这种方法通过借助特定维数模型与观测数据之间的最佳拟合来实现空间谱估计，在一定程度上提高了对低信噪比和小样本情况的适应能力，但其又因为较低的计算效率及对信号个数先验的依赖无法很好地发挥性能优势。

无论是低信噪比还是小样本情况，阵列信号处理问题本质上都属于从有限的观测数据中获得相应的参数，而近几年兴起的稀疏重构技术在解决信号缺失条件下信号恢复问题的过程中展现出了极大优势，目前在压缩感知[8]、信号分析[9]、图像处理[10]等领域已有了一定规模的应用，并取得了不错的成果。稀疏重构是指利用信号在特定变换域（如空域）上的稀疏性，从包含信号所有可能分量的完备或超完备集合中选取少量几个基函数重构原始信号的过程。目前，稀疏重构算法主要包括匹配追踪[11]、Lp范数[12]和稀疏贝叶斯[13]三类。其中，匹配追踪类算法对观测模型的稀疏度有很高的要求，在信号不同分量之间相关性较强时性能不好；Lp范数类算法的局限性则在于正则化因子参数的选取问题，具体的观测模型、信号环境等因素都会对该参数的选取产生极大的影响；稀疏贝叶斯学习方法是由Tipping[14]提出的利用贝叶斯原理与观测模型先验信息相结合的一类重构方法。目前，稀疏贝叶斯重构算法在图像处理领域的发展较为完善，在其他领域则相对滞后。

实际中，无论是具有超分辨率的子空间算法，还是稀疏重构算法，都无法达到理论估计精度，这是因为在实际中无法避免由于各种原因导致的阵列误差，包括各个阵元和通道的幅度和相位不具有一致性[15]、天线之间相互影响产生互耦效应[16]、阵元安装位置出现偏差引入的位置误差[17]等，都会使阵列流型和理想的阵列流型之间存在较大的偏差，从而使各种算法的性能出现一定程度的恶化，甚至完全失效。针对幅相误差和互耦误差共存的情况，研究人员[18-20]提出了一系列的联合校正方法，其中，文献[18]利用均匀线阵互耦矩阵的特殊结构，通过交替迭代的方式对阵列误差参数进行优化校正。文献[19]利用阵列协方差矩阵的关系式构造了一种二次代价函数，并通过交替迭代进行参数估计。文献[20]提出了基于协方差匹配技术的误差联合校正算法。文献[21]利用MIMO 系统，引入若干个经过精确校准的辅助阵元对误差及波达方向进行联合估计。

基于对当前研究现状的分析，本文针对幅相误差和互耦误差共存的情况，提出了基于信号空域稀疏性的贝叶斯测向与误差校正方法，并分析了信号测向精度及相应误差校准的理论下限，仿真结果验证了方法的有效性。

本文用到的一些数字符号说明如下。向量和矩阵均用粗斜体表示。xT和xH分别表示向量的转置和共轭转置分别表示L1 范数、L2 范数、Frobenous 范数。表示矩阵A的行列式。tr(A) 表示矩阵A的迹。(A)j,:表示矩阵A的第j行，(A):,j表示矩阵A的第j列，(A)i,j表示矩阵A的第(i,j) 个元素。xj表示向量x的第j个元素。diag(A) 表示由A的对角线元素构成的向量；diag(x) 表示对角矩阵，其对角向量对应于向量x；toeplitz(x) 表示由x形成的托普利兹矩阵。x'(ϑ)表示x(ϑ)关于ϑ的导数。Re(·) 和Im(·) 分别表示对复数进行取实和取虚操作。x⊙y表示x和y的Hadamard 积。表示给定分布概率条件下对应的期望运算符。

1 信号模型

假设在空域中有K个远场窄带信号入射到M元阵列，入射方向为，那么M×1维的阵列接收数据为

图1 阵列信号接收模型

在实际中，式(1)所对应的理想情况是不存在的，更普遍的是幅相误差与互耦误差同时存在，在这种情况下，阵列输出的计算式为

采用文献[22]中使用的离格模型，式(2)可以写为

为了进一步明确阵列输出与互耦误差系数和幅相误差参数之间的关系，对式(3)做如下变换

通过对空间角度域进行均匀采样，将式(3)和式(4)进行空域扩展，得到阵列输出的超完备表示形式为

2 模型求解

2.1 参数求解

引入中间变量γ=[γ1,…,γ L]T表示方 向ϑ1,…,ϑ L处对应的信号分量幅度的方差，即其中R=diag(γ)。

阵列输出的概率密度函数为

结合式(6)和式(7)，得到给定γ,c,δ2,β条件下的概率为

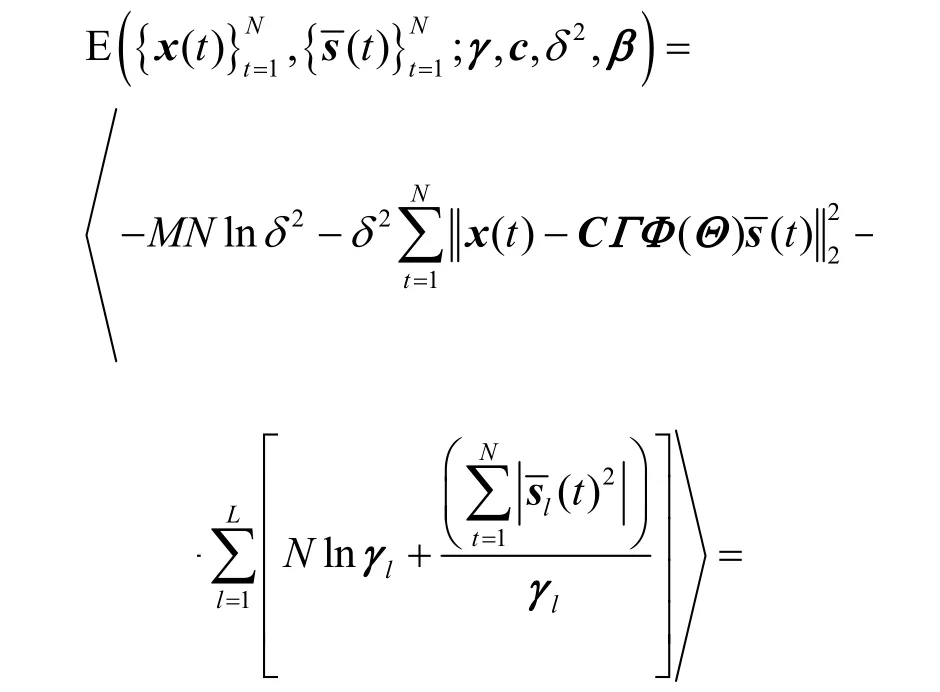
令式(11)的导数为零，可得c第q次迭代时的值为

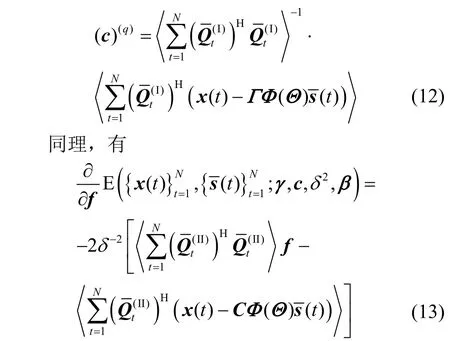
令式(13)的导数为零，可得f第q次迭代时的值为

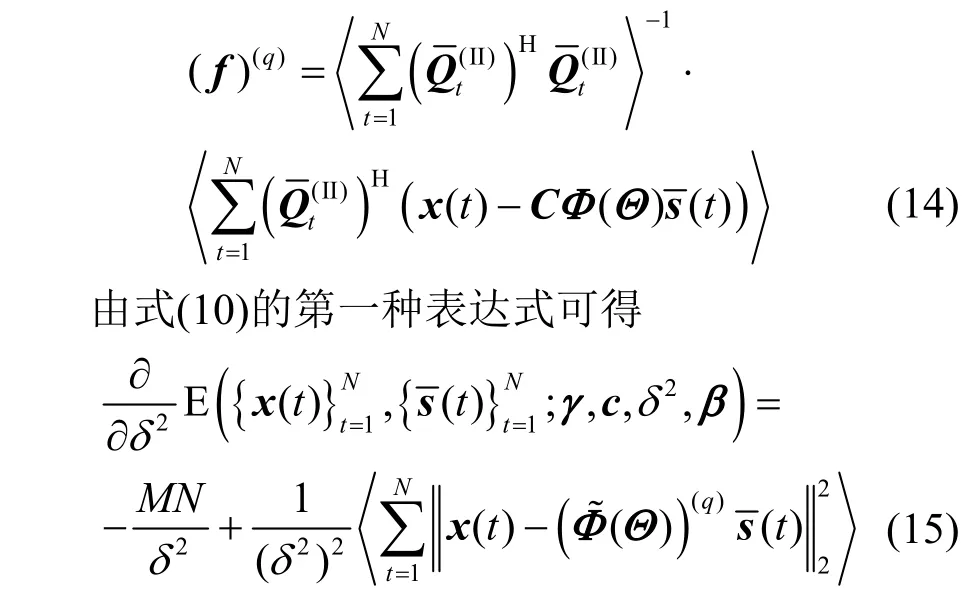
令式(15)的导数为零，可得第q次迭代时δ2的值为

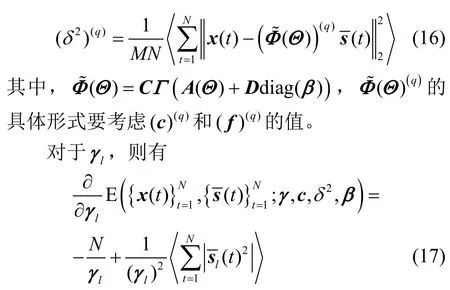
令式(17)的导数为零，可得第q次迭代时的值为

其中，constant 是一个常数余项，P是一个半正定矩阵，计算式为

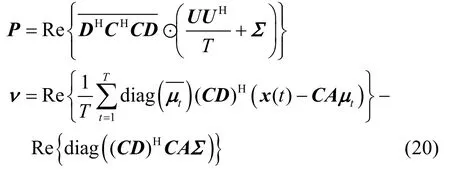
其中，μt由式(25)得到，实际上，β与是联合稀疏的，对应的K个源位置处有K个非零值，只需计算对应γl的最大K个位置处的β值，其余值设为零。因此，β、ν和P的大小可以分别减小为K、K和K×K维。

由式(19)可知

对于式(12)、式(13)、式(16)和式(18)中给出的期望值取决于条件概率密度函数并且的形式不是直观给出的，因此有必要对上述参数更新方法进行简化。

由于在t时刻，信号幅度仅与该时刻的阵列观测值x(t) 有关，根据式(6)和式(7)可以得到关于x(t) 的后验概率密度函数为

将式(26)～式(30)代入参数的更新式便可实现对参数c,δ2,γ,β的更新。而后估计出信号幅度的均值与方差，进入下一次的EM 迭代。由文献[23]可知，EM 算法具有严格的收敛性，该迭代过程逐渐逼近稳定的估计值，当迭代收敛时，由各变量的估计值便可以获得信号的空域分布、阵列误差模型和噪声功率等。

3 参数估计方差的克拉美罗界

N个阵列观测样本x1,…,xN的概率密度函数为

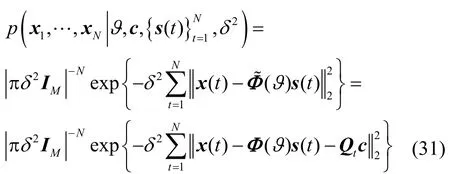
对概率密度函数（式(31)）取对数可以得到如下对数似然函数

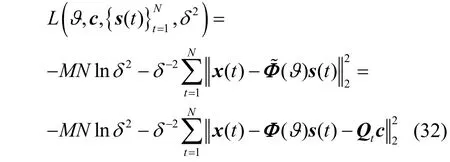
其中，ϑ和δ2是实数域上的参数，s(t) 和c是复向量。因此，将s(t) 和c分解为实部和虚部之和的形式，分别为其中，分别代表复向量的实部与虚部。经过上述分解之后，得到的参数集为

根据式(32)的似然函数，可以得到关于噪声方差δ2的克拉美-罗下界（CRLB,Cramer-Rao lower bound）为

在存在阵列互耦或者阵列幅相误差时，式(35)给出的CRLB 只是简单地将误差向量分解为实部与虚部，这并不能很好地反映出相关参数的物理属性，因此，结合文献[24]中的结论，可以将的CRLB 转化为的CRLB。这样就可以更加清晰地得出复向量c的估计精度。

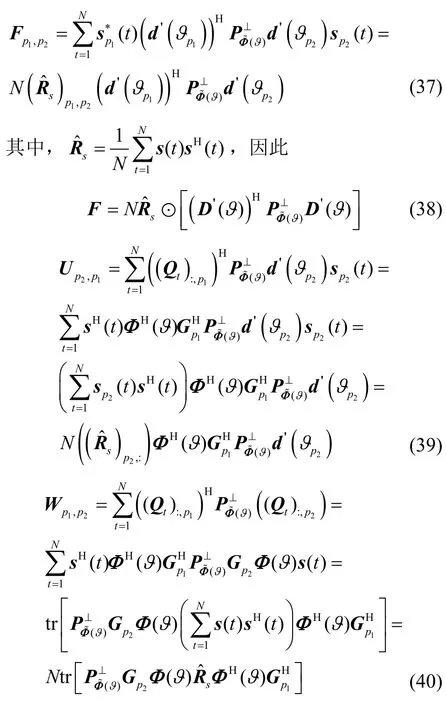
4 仿真实验与结果分析

本节将通过模拟仿真实验对本文提出的多种误差同时存在时的校正方法进行验证，下面对一些固定参数进行说明，阵列为8 元均匀直线阵，半径波长比为0.5，信号入射角度为(30.3° 36.8°)，算法最大迭代次数为1 500 次，停止阈值为10-3。采用均方根误差作为评判指标，其中，N为蒙特卡罗仿真次数，在本文中设置为为第i次迭代的估计值，ϑ为真实值。互耦系数为c=(0.6 +j0.4,0.2 +j0.1)T。值得一提的是，在这里假设第一个阵元完全校准，因此，幅度误差分别为(0 0.15 0.30 0.20 0.25 -0.20 -0.20 -0.30)，相位误差分别为(0° -20°-30° -40° 35° 25° 20° 40°) 。

4.1 校正前后的空间谱图

本节验证幅相误差和互耦误差对信号空间谱的影响，并探究本文方法对信号的分辨能力。假设2 个不相关信号以(30.3° 36.8°)的方向入射至8 元均匀直线阵，信噪比为10 dB，快拍数为100，其余参数不变。图2 给出利用本文方法误差校正前后的空间谱。其中，虚线辅助线为信号真实方向。

图2 误差校正前后的空间谱

从图2 中可以看出，在多种误差同时存在的情况下，空间谱的峰值被削弱，谱峰也发生相应的偏移，导致分辨率下降。根据文献[25]，在统计意义下，幅相误差对靠近来波方向的空间谱峰影响较大，其中，幅度误差只影响空间谱的峰值尖锐程度，不会改变谱峰的位置，相位误差则会导致谱峰发生偏移，而互耦误差则对两者皆有影响。利用本文方法对幅相误差和互耦误差进行联合估计，可以很好地对来波信号方向进行估计，提高空间谱的分辨能力。

4.2 性能分析

本节比较的方法包括离格稀疏贝叶斯推断（OGSBI,off-grid sparse Bayesian inference）、求根稀疏贝叶斯学习（rootSBL,root sparse Bayesian learning）[26]和L1SVD 算法，分别从信噪比和快拍数2 个角度对本文方法的性能进行探究，结果分别如图3～图6 所示。其中，当探究信噪比对算法的影响时，信噪比的范围为-10～10 dB，快拍数固定为100；当探究快拍数对算法的影响时，快拍数范围为10～100，信噪比固定为0，其余参数不变。

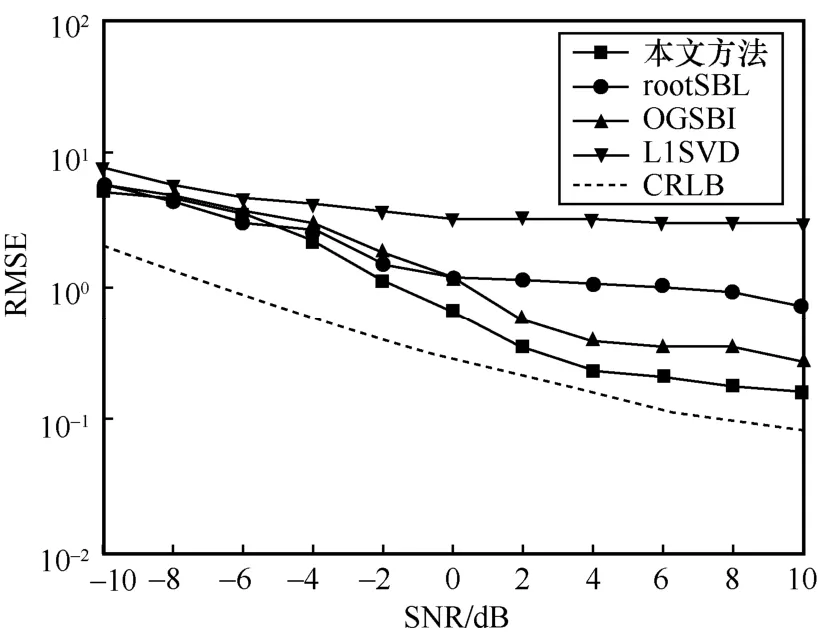
图3 信号方位估计均方根误差随信噪比变化曲线

图4 信号方位估计随信噪比变化箱线

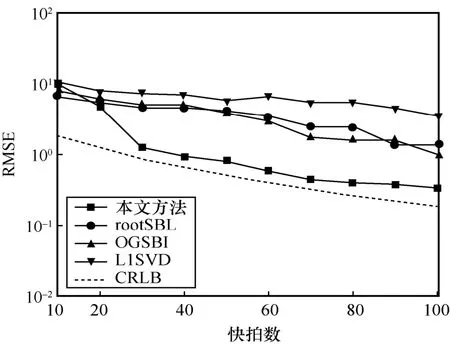
图5 信号方位估计均方根误差随快拍数变化曲线

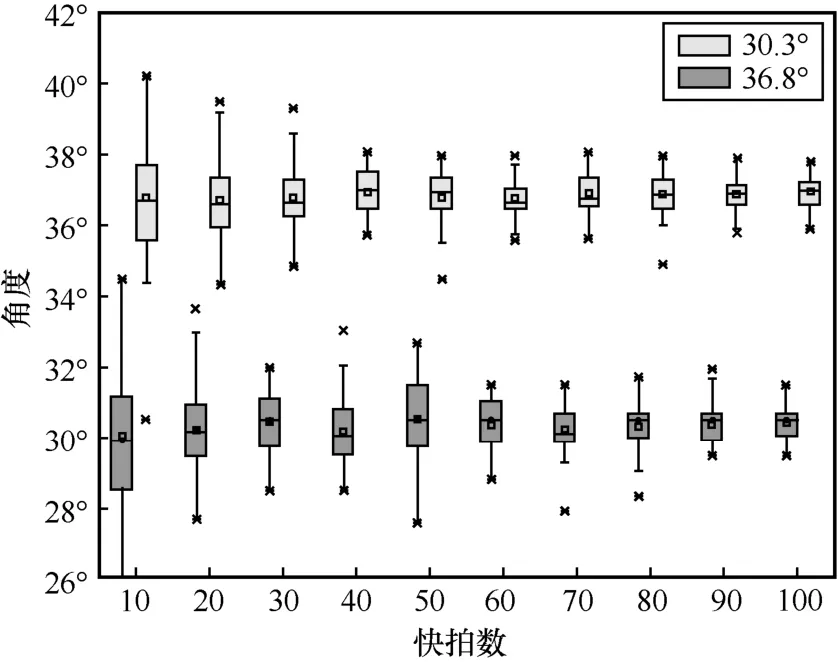
图6 信号方位估计随快拍数变化箱线

从图3 和图5 中可以看出，当分别采用信噪比和快拍数为变量时，本文方法均能达到很好的效果，且逼近克拉美罗界。在信噪比较小和快拍数较低的情况下，稀疏贝叶斯类算法中的rootSBL 和OGSBI 与本文方法表现大致相同，但随着信噪比和快拍数的增加，rootSBL 和OGSBI 算法虽然考虑了离散网格对信号方位估计造成的影响，但互耦误差的存在使估计的空间谱伪峰较高，一定程度上限制了这2 种算法的性能。L1SVD 算法未考虑网格误差的影响，效果最差。

从图4 和图6 中可以看出，随着信噪比和快拍数的提升，箱线图中的中位线逐渐逼近真实的来波方向，整体的波动程度迅速下降。2 次实验的蒙特卡罗次数均为100 次，直观来看，当信噪比提升时，箱线图的波动程度相比于快拍数增大时收敛得更快，箱体更小。

将快拍数设置为 10～100，信噪比设置为-10～10 dB，其余条件保持不变，绘制互耦误差和幅相误差随信噪比快拍数的变化曲面，分别如图7 和图8 所示。

图7 互耦误差随信噪比快拍数变化曲面

图8 幅相误差随信噪比快拍变化曲面

从图7 和图8 中可以看出，随着信噪比和快拍数的提高，互耦误差和幅相误差曲面均能迅速下降，其中，互耦误差曲面比幅相误差曲面整体偏低的原因有2 个：1) 在观测模型中，幅相误差与信号方向之间的相互耦合效果要比互耦误差与信号方向之间的耦合效果强；2) 采用实验值与真实值之间差值的二范数作为评价指标，本文中互耦误差系数只有2 个，幅相误差系数则有8 个。

表1 和表2 是在信噪比为10 dB、快拍数为100、其余条件与上文保持一致条件下的互耦系数和幅相系数估计结果。

表1 互耦系数估计结果

表2 幅相系数估计结果

5 结束语

本文提出了幅相误差和互耦误差同时存在时基于稀疏贝叶斯算法的求解方法。该方法共包含2 个阶段，第一阶段，在空域稀疏的前提下构建了误差存在时接收信号的超完备模型，得到接收信号的后验概率密度函数。由于密度函数具有极强的非线性，直接优化十分困难，第二阶段采用EM 算法对该函数进行迭代优化求解相应参数。此外，本文还推导了相应参数的克拉美罗界。仿真实验结果表明，本文方法测向性能优于OGSBI、rootSB 和L1SVD 中的方法，同时能够对幅相误差和互耦误差进行有效的校正。