基于残差的逆变器滤波电路故障检测与分离方法研究*

萧声亮，董 冲，莫程凯，金晴晴

（南华大学电气工程学院，湖南衡阳 421001）

0 引言

近年来，随着全球节能减排和碳中和时间表的提出，各国对于清洁能源的需求增加，风能、光能等能源发电也得到快速发展，而逆变器作为关键部分被广泛使用。由于开关器件的开通关断的快速变化、温度和时间老化等因素导致逆变器容易发生故障，因此如何识别所有故障类型并准确定位成为非常重要的环节。

逆变电路的故障诊断理论研究较多，很多理论趋于完善，其相关技术可以分为3 种基本类型：基于解析模型的方法、基于信号处理的方法和基于机器学习法，这3 种类型都各有优缺点。基于模型的方法使用系统的分析知识，通常基于使用参数估计、奇偶方程或状态观测器的残差生成，在最近几年里研究重点主要集中在鲁棒性问题上，由于数学模型的使用这是一个自然和必要的关键步骤。基于解析模型[1-2]的方法缺点在于易受模型准确性、系统参数及噪声的影响。基于信号处理方法可以是时域[3-4]的，也可以是频域[5-6]的，一般通过小波变换、电流Park矢量变换和频谱分析等信号处理方法对系统的幅值、频率等信息进行处理、分析进行故障诊断，再与神经网络、支持向量机、深度神经网络、模糊逻辑等智能方法相结合识别故障类型。基于信号处理[7-8]的诊断方法缺点是需要较多计算能力、时间较长和复杂性较高。在机器学习法方面，Lei Y 等[9]致力于将机器学习技术应用于机器故障诊断，为将机器学习方法应用于故障诊断提供了极好的见解，并详细总结了该研究领域的基本思想概念和方案。迁移学习技术[10]在机器学习中被视为下一代的关键技术之一。Yang B[11]报道了一个将迁移学习技术应用于故障诊断的成功案例。机器学习法[12-13]缺点在于较依赖于对经验知识的获取、庞大知识库和维护复杂。

目前在国内外应用残差来检测故障的研究也开展了不少，Hao L 和Steven X Ding 进行了PnP 过程监控系统的自适应迭代残差发生器设计[14]和残差集中控制和检测，Wang Y[15]研究了基于降压和升压变换器的恒流恒压锂电池充电器的故障检测与分析。本文采用基于残差的逆变器故障诊断方法隶属于基于解析模型的方法的类别，通过仿真实验验证和提取数据分析证明了此方法的可行性。

1 逆变器模型的建立

在本文首先提出用于描述逆变器在标称值和故障运行条件下的动态的建模框架，使用如图1 所示的逆变器拓扑作为研究对象[16]。

图1 逆变器拓扑结构

1.1 无故障的系统模型

对于一个单相、两电平、带LC 滤波器的SPWM 逆变器，不管是半桥还是全桥或者单极性和双极性调制，都可以用图2所示电路模型表示[17]。电阻r 表示导线的电阻、滤波电感附带的等效电阻等，电流源用于等效负载所消耗的电流，其电流的大小随负载的大小而变化。

图2 单相逆变器等效电路

设逆变器工作在双极性SPWM 方式，这里分别选择滤波电感电流iL和滤波电容电压uc为状态变量，选择开关函数s表示电源电压的极性（这里定义当s=1 时输出为正方向电压，当s=0是输出为负方向电压），根据图2得到逆变器的状态方程为：

若将Vd看作为一个非理想的与时间有关的输入变量，则式（1）所表示的就是一个非线性时变的状态方程。若将Vd看做是理想的（恒定不变），那么可认为它是一常数而不是输入变量，则式（1）可写成：

对模型进行改变之后，状态方程的系数矩阵都与开关状态函数s无关，即无论s为任意状态，这些系数矩阵都是相同的。而输入向量由时变的(2s-1)Vd和负载扰动电流I构成，这就将因SPWM 控制导致的时变系统变成了时不变系统。利用状态空间平均法[18]对开关函数求取平均值：

式中：M为调制比。

综合上述分析逆变器前面的模型输出的电压可以等效为：

通过式（2）和式（4）可以得出如图3 所示的逆变器状态空间平均模型框图。为了验证搭建的逆变器状态空间平均模型框图是否正确，将系统模型框图通过GeckoCIRCUITS 搭建与电路图得到的波形进行比较验证。搭建的模型得到图4 所示的波形，通过与电路波形可以发现波形基本重合，由此可以认定建立的模型是正确的。

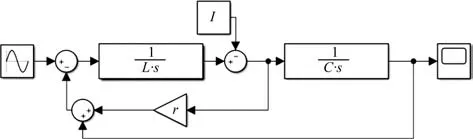
图3 逆变器状态空间平均模型

图4 逆变器状态空间平均法波形

1.2 故障后系统建模

在本文中只考虑无源元件的故障即电容与电感的数值变化引起的故障。通常无源元件的元件故障和，可以认为无故障的A和B与附加故障偏差ΔA和ΔB的代数和，因此故障下的状态可以建模为：

其 中=A+ΔA和=B+ΔB通过代数运算可以将式（5）中的状态方程转换成式（6）附加故障向量与其系数矩阵的形式。

式中：x∈Rn,u∈Rm,y∈Rp，分别为对系统的状态向量、输入向量和输出向量；f为一个向量，包含具有适当维数的附加故障；A、B、Bf分别为系统的状态向量、输入向量和故障向量的矩阵系数；由于利用单一信号的检测和分离是本研究的重点，所以p=1，也假设m=1，因为单一脉宽调制信号（SPWM）主要控制开关元器件。

以电容故障为例，假设故障导致电容变化了ΔC，则通过代数运算可以得到电容附加故障向量f和系数Bf：

这里定义e(t)=z(t) -x(t)其中z(t)为实际测量状态向量的值，则产生的动态误差为：

将系统输出y(t)与参考信号yref即无故障时的输出值进行如下比较，生成残差信号:

假设系统是一个稳定的系统，即其特征值的实部绝对为负，则满足当f=0 时，误差e和残差信号r在一段时间后趋于零，当f≠0时，误差e和残差信号r变为非零。

假设被测信号y(t)对故障是敏感的，即故障是可观测的。理想情况下即在无故障条件下，残差为r=0。然而，由于测量噪声和模型的不确定性，残差信号在正常（无故障）条件下可能不完全为零。在故障情况下，残差信号改变，并显示出与正常情况的偏移。在对故障检测和后续隔离做出任何决定之前，残差信号需要进一步评估。本文提出了一种利用单一残差信号和残差评价函数来检测逆变器故障的方法：

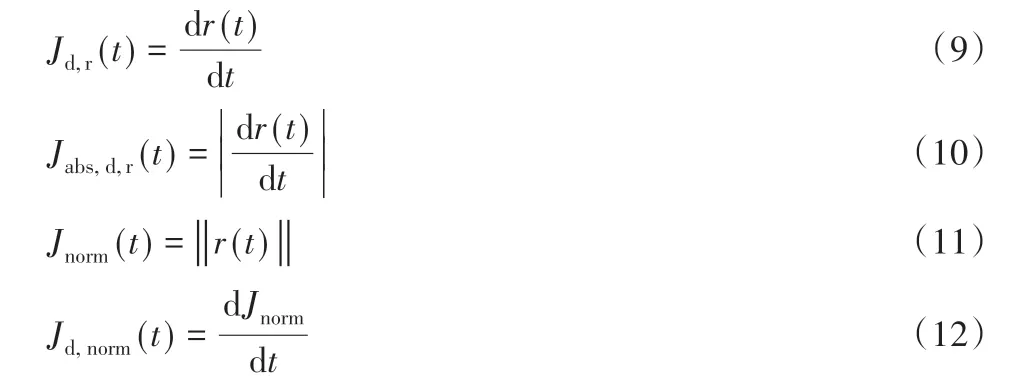
式中：Jd,r为残差信号斜率；Jabs,d,r为残差信号斜率绝对值；Jnorm为残差信号范数；Jd,norm为残差信号范数斜率。

假设Tsf为系统的样本时间，k为时间指标，‖r(t) ‖为残差信号的欧氏范数，则：

式中：rT为r的转置矩阵。

2 仿真实验搭建与结果分析

按图1 所示搭建电路，滤波器采用LC 滤波，直流电压Vd=350 V，载波比200，调制比M=0.9，电感L=13 mH，电容C=16 µF，导线内阻及电感附加等阻值r=0.2 Ω，负载电阻R=20 Ω，ƒ=50 Hz。在电路0.04 s的时候，模拟电感值和电容值分别下降了10%和50%的故障，可得到残差信号、残差信号的绝对值、残差信号的斜率、残差信号斜率的绝对值、残差信号范数和残差信号范数斜率。以残差信号范数和残差信号范数斜率的曲线为例，进行故障分析与隔离。由于范数具有累加效应，所以需要选择一定的累加周期，每个周期结束后将重新进行求范数，因逆变器具有周期性，故在这里取SPWM 波的一个周期作为累加周期。图5 和图6 所示分别为电容值和电感值下降了10%和50%故障时的残差信号范数和残差信号范数斜率。

图5 电容值和电感值降低10%与50%时的残差信号范数

图6 电容值与电感值降低10%与50%时的残差信号范数斜率

针对残差生成的范数和范数斜率的曲线图，可以看到在没有故障的时候（即0.04 s 之前）残差生成的范数和范数斜率的值都趋于零，当故障发生的时候（0.04 s 之后）两者的值趋于非零的状态，故可以定于阈值来检测是否发生故障也能用阈值来对不同的故障进行分离。以残差信号范数为例，分别取阈值Jnorm为0.005、0.035、0.060 和0.12 将电容电感4 个故障分离开来。根据阈值给出故障检测与分离的算法流程如图7所示。

图7 故障检测与分离的算法流程

为验证方法和选取阈值的正确性，采用多种数据来模拟故障。如表1所示，当故障在30 ms和50 ms出现，电感电容值分别降低到原先电感电容的10%到50%之间和超过50%的数值时，稳定之后可以看到残差信号范数的值维持在所设定的值变化之内。

表1 随机模拟4组故障情况下，查看残差信号范数的值

3 结束语

本文提出基于残差的逆变器滤波电路故障诊断与分离的方法，该方法在状态空间平均法建立的数学模型基础上进行了实验实施和验证，证明了基于残差的故障诊断与分离对于逆变器故障的实用性。实验结果表明，通过该方法能有效地检测和分离逆变器的电容和电感值变小的故障。本文所提出的与其他故障诊断方法相比较，无需增加过多的硬件结构和过于复杂的运算能力。此外，将基于残差的故障诊断与分离的方法，用于除逆变器意外的故障、研究更多的残差评估函数以及确定检测和分离的过程时间都是需要进一步研究的课题。