基于学生知识追踪的多指标习题推荐算法

诸葛斌，尹正虎，斯文学，颜蕾，董黎刚，蒋献

（浙江工商大学信息与电子工程学院，浙江 杭州 310020）

0 引言

随着教育信息化和移动端应用的加速普及，在线教育打破了传统教学的时空壁垒，学习者可以随时随地进行线上学习，海量的习题和教学资源能够充分满足不同层次学习者的学习需求，吸引大批用户来到线上平台学习。在这个信息爆炸的时代，线上教育资源也在呈指数级增长，然而这些资源的质量参差不齐，极大地增加了学习者选择学习资源的难度，而个性化推荐技术恰能解决这一难题。因此，如何利用推荐技术从海量的线上资源中为学习者提供精准、个性化的习题推荐，让学习者能更高效地学习，是在线教育急需解决的问题。

传统的习题推荐技术主要分为两类，一类是基于内容和基于邻域的协同过滤推荐[1-2]，这是推荐系统中应用最为广泛的推荐算法，主要根据学生的历史学习记录，找到与目标学生兴趣相似的近邻学生，无须考虑习题的具体属性。其中Li等[3]搭建了一个在线教育平台，通过协同过滤算法为用户推荐个性化课程；吴云峰等[4]针对协同过滤推荐法中用户的历史信息不足等问题，提出基于多分类器的迁移Bagging习题推荐算法；Segal[5]等设计了一种针对学生的个性化教育算法，首先通过UserCF对相似学生进行排序，再为目标学生的习题构建一个“难度”排名，可辅助教师为学生布置个性化作业和考试。虽然基于UserCF的推荐方法结构简单、可解释性强，但这类算法忽略了不同学生知识掌握水平的差异，只能粗粒度地对学生进行分类，无法满足智慧教育的个性化习题推荐要求。

另一类是基于认知诊断的推荐技术，如Ozaki[6]提出了传统DINA模型，该方法将习题的知识点考查矩阵作为输入，得到学生的认知掌握向量，然后根据学生认知情况向目标学生个性化推荐习题。Bang等[7]提出了一个通用神经认知诊断（neural cognitive 2iagnosis，NeuralCD）框架，结合神经网络学习复杂的运动交互，将学生和练习投射到因子向量上，并利用多个神经层对其交互进行建模，以获得准确且可解释的诊断结果。Liu等[8]提出了一种模糊认知诊断方法框架（fuzzy cognitive 2iagnosis framework，FuzzyCDF），用于考生对客观和主观问题的认知建模，结合模糊集理论和教育假设来模拟考生的行为，通过考虑失误和猜测因素对每个问题进行评分。项目反应理论（item response theory，IRT）是一种经典的认知诊断方法，它可以为分析学生表现提供可解释的参数（即学生潜在特质、问题辨别和难度）。Cheng等[9]提出了一个通用的深度项目反应理论（2eep item response theory，DIRT）框架，利用深度学习提取问题文本的语义表征，从而增强传统的认知诊断IRT。基于认知诊断的方法能够考虑学生的知识状态，再基于学生个人的知识水平做出推荐，但是没有将相似学生的信息加入参考，忽略了学习的群体性，推荐的多样性受限。

为了弥补上述两种算法的不足，本文提出了一种基于学生知识追踪的多指标习题推荐（stu2ent knowle2ge tracking base2 multi-in2icator exercise recommen2ation，SKT-MIER）方法，首先对学生知识概念学习情况进行深入研究，利用LSTM神经网络对学生知识点学习范围进行预测，以便对未答知识点或答错知识点的相关习题进行优先推荐；利用更先进的深度知识追踪模型对学生的知识点掌握情况进行建模，从而得到学生当前知识状态，预测其在未来学习中的表现；其次融入UserCF算法，结合学生相似群体之间的学习情况，从而提高推荐的多样性。综上所述，本文的主要创新和贡献如下：

· 提出了一个结合学生遗忘规律的知识概率预测模型SF-KCCP，得到学生的知识点学习范围向量，保证推荐习题的新颖性，有利于学生学习新知识；

· 基于DKVMN模型，得到学生的知识点掌握水平向量，确保推荐习题难度适当，有利于激发学生的学习热情；

· 将上述两组向量值为计算依据，利用协同过滤算法得到相似学生，结合学生自身和其相似学生的知识水平进行推荐，提高习题推荐的多样性，有利于帮助学生对未掌握的知识点进行查漏补缺；

· 在4个真实开源的数据集上对本文提出的推荐模型进行评估，并与其他主流模型进行对比，SKT-MIER在相应的评价指标上均有所提高。

1 深度知识追踪概述

知识追踪是根据学生过去的答题情况对学生的知识掌握情况进行建模，从而得到学生当前知识状态表示的一种技术。早期的知识追踪模型是基于一阶马尔可夫模型的，但其有着明显的缺陷，随着技术的进步，有研究将深度学习（2eep learning，DL）技术引入知识追踪领域，最早基于DL的知识追踪模型来自美国斯坦福大学的深度知识追踪（2eep knowle2ge tracing，DKT）[10]，文献[10]提出利用递归神经网络（recursive neural network，RNN）对学生的学习情况进行建模，将学生过去的学习活动压缩在隐藏层中，映射学生对不同知识概念的掌握水平，以此预测学生未来的答题正确率。DKT在不需要过多专家经验和大量特征工程的情况下，精度优于传统方法。针对DKT算法预测结果的一致性与波动性问题，Yeung等[11]提出了在DKT算法的损失函数中加入3个正则化项的方法，增强了算法预测的精度，使知识状态转移更为平滑。Zhang等[12]在练习层面加入了更多的特征，并使用自动编码器将高维信息转换为低维特征，提升了模型性能。为了更好地把握学生做题情况的历史关联性，神经教学代理[13]（neural pe2agogical agent，NPA）模型利用双向长短期记忆网络对学生知识状态进行建模，该网络配备了一个注意层用来对学生的学习历史进行重点分析，从而得出更准确的预测。

除了基于RNN架构的知识追踪模型，Zhang等[14]提出了基于动态键值对网络的知识追踪模型DKVMN。它借鉴了记忆增强神经网络的思想，依赖于外部存储器中的读写操作，比RNN和LSTM更适合对大量的学生答题记录进行建模，解决了RNN类模型难以评估学生对每个知识点的掌握程度的问题。DKVMN模型网络结构如图1所示，其包含一个读过程和一个写过程，使用键值对存储器结构而不是单个矩阵。其中包含了一个静态的键（key）矩阵kM，用来存储所有习题包含的所有知识点，是不可变的；一个动态的值（value）矩阵vM，根据擦除向量和增加向量存储并更新学生对于各个知识点的掌握情况，是可变的。

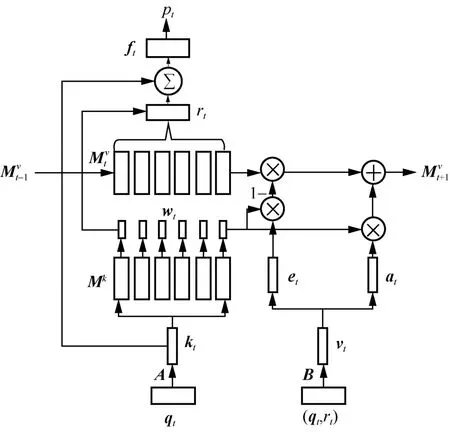
图1 DKVMN模型网络结构

在每个时间戳，DKVMN模型有两组输入，第一组输入为离散的练习题标签qt，对应输出正确回答qt的概率p （ rt= 1|qt），第二组输入为题目和回答元组(qt,rt)，用来更新下个时间步的值矩阵。其中，qt属于具有若干个不同练习的集合Q，rt为该题是否正确回答的二值表示。假设Q包含m个知识点概念{k1,k2,k3,… ,km}，那么这些概念存储在键矩阵 Mk（大小为 m ×dk）中。学生对每个知识点的掌握程度，即知识点掌握水平状态则会存储在值矩阵中（大小为 m ×dv），显然该矩阵随时间变化，输入学生的每一条做题记录作为更新依据。kt为习题嵌入向量，由输入qt和嵌入矩阵A相乘得到。kt与 Mk矩阵中每个知识点向量进行内积，再通过激活函数Softmax计算权重向量wt，它代表了习题和每个概念之间的关系：

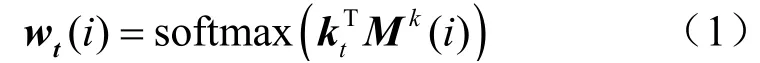
（1）读过程

读过程可以实现对学生答题情况的预测，当练习题tq来临时，首先通过计算权重向量tw得到该习题包含哪些知识点，继而将 tw与值矩阵求内积，得到该学生对于答对这道题所需的知识点的掌握情况，如果掌握了大部分知识点，则估计该学生答对这道题的可能性较大，具体计算式如下：

尽管有些题目包含的知识点内容相同，但每个习题其自身的难度不一，因此将学生对练习的掌握程度tr和输入练习嵌入向量tk连接，再通过具有tanh激活的完全连接层获得总结向量tf，就包含了习题本身的难度：

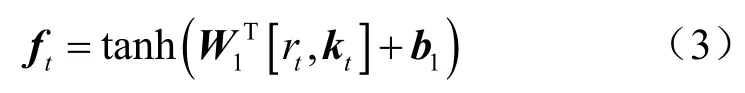
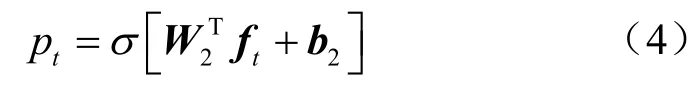
（2）写过程

写过程根据学生的实际答题情况实现对学生知识点掌握情况的更新，体现在值矩阵的动态改变上。输入答题记录元组(qt,rt)得到学生的知识增长向量tv，在对值矩阵进行更新之前，先模仿LSTM的输入门和遗忘门进行记忆擦除和新增操作，从而更符合现实中学生的遗忘规律和记忆强化规律。

计算擦除向量te：

其中，E为变换矩阵，使得te成为一组列向量且每个元素取值均在(0,1)内。上一时间步的值矩阵经过擦除之后如下：

计算更新向量ta，其中，TD表示需训练的权重矩阵，ab表示需训练的偏置参数向量：

其中，ta为行向量，经过更新之后得到下一个时间步的值矩阵：

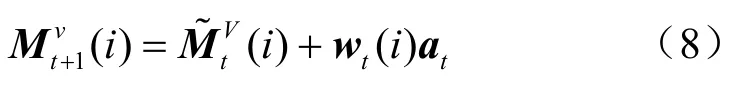
如式（9）所示，在训练过程中，嵌入矩阵A和B以及其他参数和 Mk、Mtv的初始值通过最小化tp和真实标签tr之间的标准交叉熵损失来共同学习：

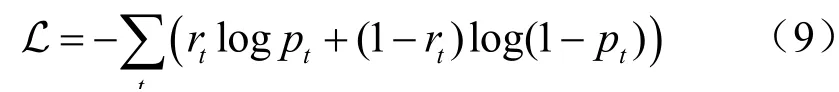
2 基于学生知识追踪的多指标习题推荐方法

本文提出的多指标的习题推荐系统框架如图2所示，采用一种先筛选后过滤的模式，首先根据SF-KCCP模型从原始题库中筛选符合当前学生知识点学习范围的习题，得到预备习题库。在此基础上，采用基于用户的协同过滤算法过滤，将学生知识点学习范围向量和学生知识点掌握程度向量作为相似学生的评判指标，然后计算学生间的余弦相似度，选择相似度排名大于一定阈值（通常为0.95）的学生作为相似用户，计算相似用户的平均知识点掌握程度，最后根据设置的期望难度，过滤得到推荐习题集。

2.1 习题初筛模块

对于目标学生在某个做题时间t，首先通过初筛模块生成符合学生知识点学习范围的习题库EBp。习题初筛结构如图3所示。首先将学生做题记录 tX输入SF-KCCP模型对学生已学知识点情况进行建模，预测下一时刻学生需要学习的知识点向量并将其与原始习题库中每道习题真实包含的知识点向量 tK进行计算，得到它们的相似性分数tω，相似性分数越高，越符合学生需要学习的知识范围，最终选择符合要求的前N个习题e组成EBp。算法 1描述了EBp的计算过程。相似性分数计算式如下：

图3 习题初筛结构

2.1.1 融入遗忘规律的知识点学习范围预测模型

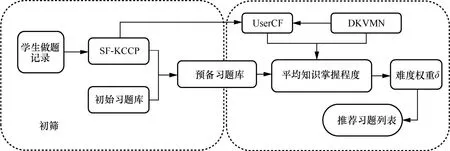
图2 多指标的习题推荐系统框架

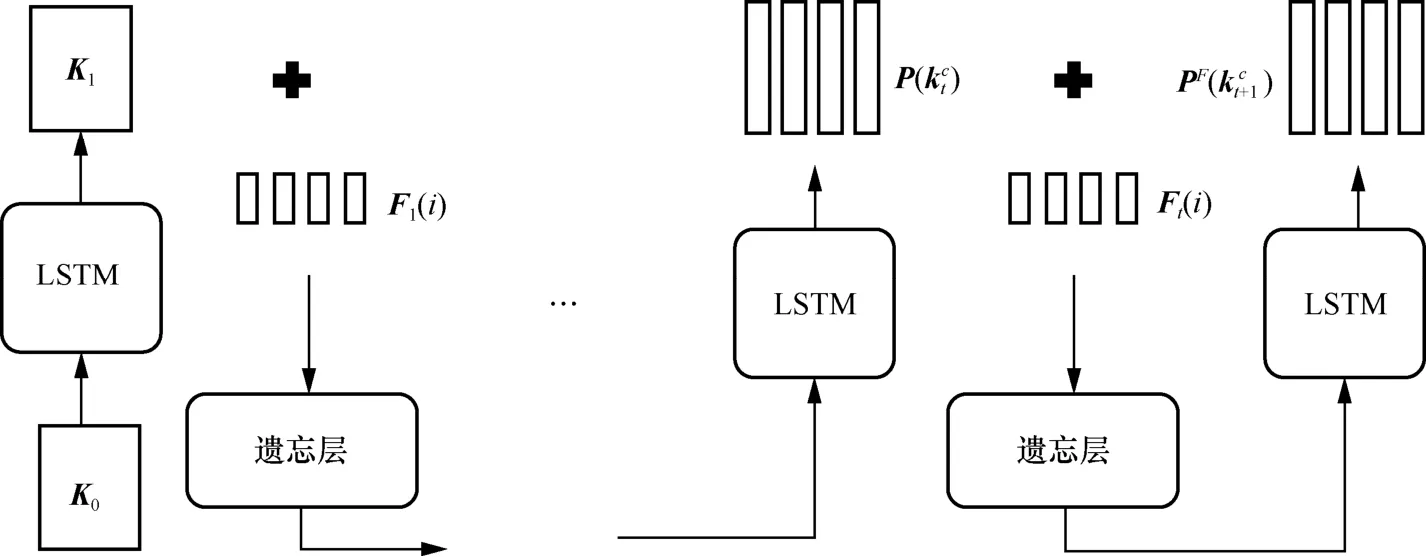
图4 SF-KCCP模型

著名的艾宾浩斯遗忘曲线理论展示了学生对所学知识的遗忘规律[15]，遗忘的速度呈现先快后慢的趋势。遗忘带来的影响是学生知识点学习范围的缩小，之前学过的知识点也会随着时间的流逝被逐渐遗忘，从而转变为未学知识点。影响遗忘的具体因素有学生重复学习知识点的次数与距离上次学习该知识点的时间间隔。SF-KCCP模型如图4所示，其由本文将遗忘规律定量地融入预测模型中而得到。

2.1.2 知识点学习范围预测

利用知识概念从0到t的出现顺序来预测每个知识概念在t+1时刻的出现概率，因此知识点学习范围预测是一个基于顺序的预测问题，可以采用LSTM获得序列预测模型。基于LSTM的知识点学习范围预测模型如图5所示，其中标记为A的圆角矩形表示模型在时刻t的状态。输入矩形 tK表示在时刻t出现的知识概念，从做题记录 tX中得到；输出矩形 1t+K表示通过模型预测得到的在时间1t+知识概念出现的概率。

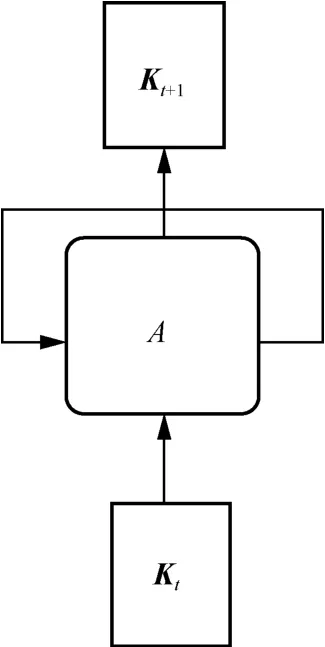
图5 基于LSTM的知识点学习范围预测模型

在被输入网络之前，先对 tK进行独热编码[16]，结果表示为φ (Kt)。模型的输出 Kt+1是一个维度等于所有知识概念数量的向量，表示对下一时刻知识概念出现的预测，而1t+时刻模型的输入记为φ( Kt+1)即真实的知识点学习向量。依据LSTM模型，在一个训练周期T结束后对知识点学习范围预测问题进行建模，使用二元交叉熵损失构造一个损失函数对模型进行训练。

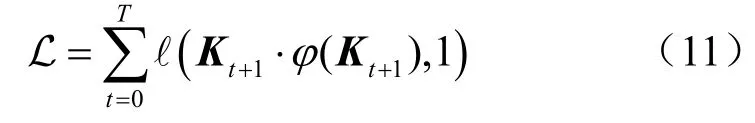
最终模型的输出是一个向量，其长度等于课程中所有知识概念的数量，表示为：

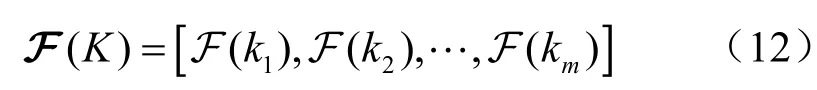
其中，F (ki)表示第i个知识概念在t+1时刻出现的概率。为了满足推荐的新颖性，让已经回答正确的知识概念在以后的练习中尽量少出现，模型赋予学生答题过程中未答知识点和回答错误的知识点更大的权重，即在LSTM网络的输出层添加一个权重向量，其长度等于知识概念的数量：

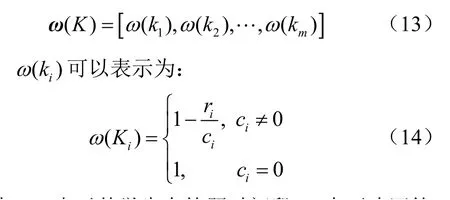
其中，ir表示某学生在答题时间段T内正确回答知识点 iK的次数，ic表示T时间段内知识点 iK出现的次数。通过LSTM模型的输出与权重向量的结合可以得到下次练习中知识概念的出现概率向量，即

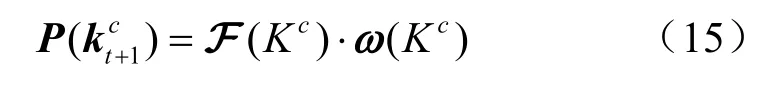
2.1.3 融入学生遗忘规律

将距离上次学习相同知识点的时间间隔因素记为SK（same knowle2ge），将重复学习相同知识点的次数因素记为RT（repeat times），这两个标量组合得到向量表示学生对知识点i的遗忘程度。受LSTM网络的启发，采用全连接网络计算记忆擦除向量和记忆更新向量来拟合遗忘行为，与第2.1.2节中得到的相结合得到新的知识点学习范围

遗忘处理过程如图6所示，将影响学生遗忘的因素Ft(i)与t时刻学生的知识点学习范围嵌入矩阵进行遗忘处理，得到学生本次学习开始时的知识点学习范围嵌入矩阵。受LSTM中遗忘门与输入门的启发，根据影响知识遗忘的因素Ft(i )更新 时，首先要擦除中原有的信息，再写入信息。其中，擦除过程控制学生知识点学习范围的衰减，写入过程控制学生知识点学习范围的更新。

图6 遗忘处理过程

利用一个带有Sigmoi2激活函数的全连接层实现擦除过程，具体计算式为：

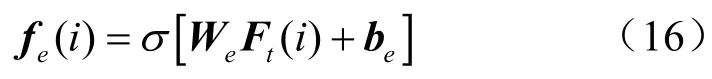
其中，σ表示Sigmoi2激活函数，eW为权重矩阵，形状是全连接层的偏置向量eb为vd维。

利用一个带有tanh激活函数的全连接层实现更新过程，具体计算式为：

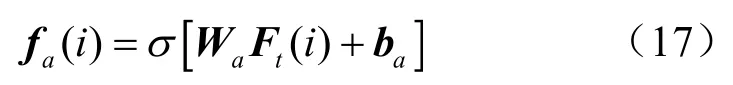
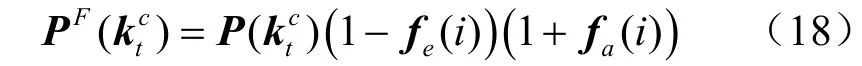
习题初筛模块的算法描述如下。

算法1 习题的初筛算法

输入：Xt, EB, N {做题记录,习题库,需要的题数} 输出：EBp{预 备习题库}

2.2 习题再过滤模块

2.2.1 计算相似学生用户

本节介绍了如何基于SF-KCCP模型与DKVMN模型得到目标学生的相似用户S′，再通过相似用户计算每个目标学生的平均知识掌握程度gi。算法 2描述了gi的计算过程。其中，PF(kc)( m ×n)表示确定时刻学生的知识点学习范围矩阵，m表示学生个数，n表示知识点数量；p(m×z)表示学生知识掌握水平矩阵，z表示题目数量。假设学生i与学生j的pj={d1,d2,… ,dz}，则学生i与学生j的余弦相似度计算式如下：

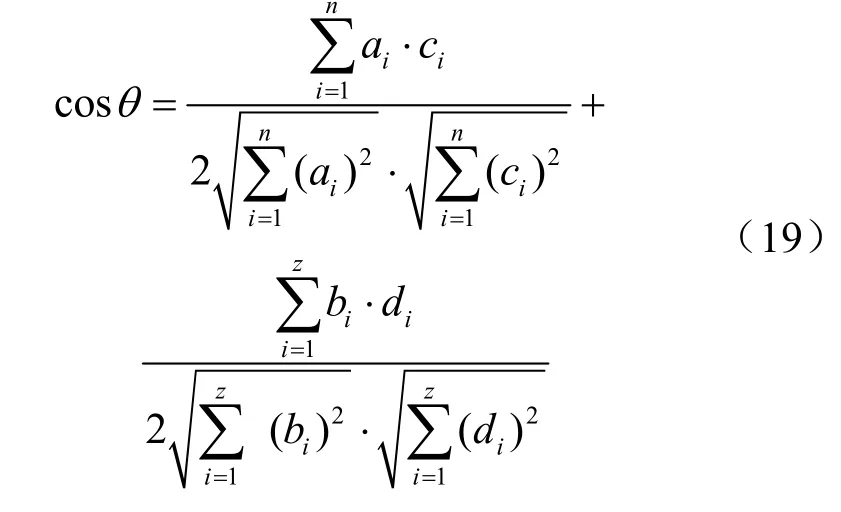
对于目标学生i，其最终的平均知识掌握程度计算式如下：

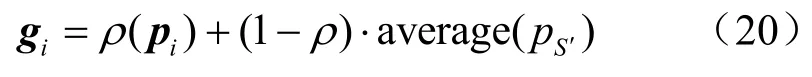
其中，average(pS′)为与学生i相似的所有学生的知识掌握水平向量平均值，gi由学生个人的知识水平pi和相似学生的共性知识水平average(pS′)按一定的比例相加得到，比例由参数ρ调节，ρ的取值范围为[0, 1]。ρ越大，学生个人知识水平产生的影响越大，这里 ρ= 0.7。

计算学生的平均知识掌握程度算法描述如下。

算法2 学生的平均知识掌握程度算法

输入： PF(kc)( m ×n),p( m ×z),S{学生的知识点学习范围矩阵, 知识掌握水平矩阵, 学生}

输出：g{所 有学生的平均知识掌握水平}

2.2.2 再过滤算法

在进行习题推荐时，考虑学生个人的知识掌握水平既可以使推荐结果更具针对性，又能对推荐题目的难度把控更到位。而加入UserCF算法可以结合学生相似群体之间的学习情况，提高推荐结果的多样性。

为了达到上述目的，习题再过滤结构如图7所示，设置习题再过滤模块用于对初筛后的预备习题库进行二次过滤。ig表示学生i的平均知识掌握程度向量，每一位的值越大代表学生i答对该题的概率越大，即该题对该学生来说难度越小，因此可以使用1i-g表示学生i的习题预测难度向量。其中iδ表示推荐题目的期望难度，它可以是一个适当的难度范围，表示向学生推荐正确概率为iδ的题目。标有Distance的圆角矩形是一个计算习题预测难度和期望难度iδ之间距离的过程，预测难度即1i-g。在获得每个练习的预测难度与期望难度之间的距离|δi-(1 -gi)|后，通过设定最大权重值 Ωi对练习进行排序，并选择所有小于 iΩ的n个练习组成最终的输出练习集

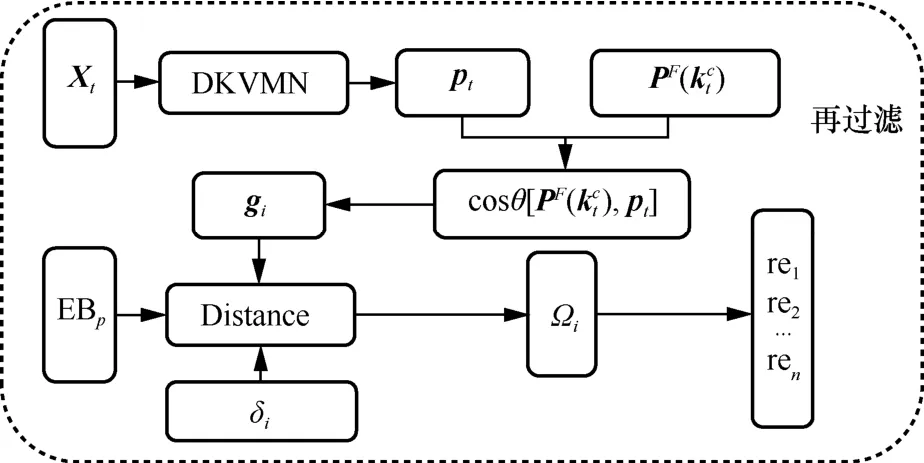
图7 习题再过滤结构

3 实验分析与讨论

3.1 数据集

本文的实验部分使用了3个数据集作对比分析，分别是ASSISTment2009、Statics 2011以及本文作者团队自主开发的智慧在线教育系统DouDouYun的数据集，3个数据集的缩写分别是ASST09、STATICS、DouDY，数据集简介见表1。

表1 数据集简介

3.2 对比模型

实验将本文提出的推荐算法与以下3个基线模型进行对比，分别是基于学生的协同过滤[17]（stu2ent-base2 collaborative filter，SB-CF）、基于习题的协同过滤[18]（exercise-base2 collaborative filter，EB-CF）以及马骁睿等[19]提出的基于协同过滤的深度知识追踪（2eep knowle2ge tracking base2 on collaborative filtering，DKT-CF）模型方法。

（1）SB-CF

该模型参考协同过滤的思想，为特定用户寻找感兴趣的内容，在习题推荐中基于学生相似度进行推荐，根据学生的做题记录构建学生之间的相似度矩阵，然后识别得到与目标学生答题情况最为相似的前10名学生，再从每个相似学生的答题记录中抽取适合难度的题目进行推荐。

（2）EB-CF

该模型参考物品之间相似度进行推荐的思想，利用项目的内在品质或者固有属性进行推荐，在习题推荐中根据学生的习题作答情况为每个习题设置难度权重，然后计算习题相似矩阵并从中提取和已做练习相似的习题，再根据想要的习题难度权重进行推荐。

（3）DKT-CF

该模型通过深度知识追踪模型DKT对学生知识状态建模，再结合相似学生的信息进行协同过滤推荐，使推荐结果既考虑学生个人的知识状态又考虑群体学生学习的共性，提高了推荐结果的可解释性和准确性。

3.3 评价指标

本文结合多种算法实现了一个多指标的习题推荐系统，多指标指的是练习的难度、新颖度和多样性。其中，习题难度会影响学生答题的正确率，从而影响学生的使用体验，所以难度对于推荐习题的质量把控起到最为关键的作用[20]；推荐习题的新颖程度能够给学生提供一种惊喜感，有助于学生对新知识点的学习；多样性则能够方便学生查漏补缺，对于所有知识点进行一个更为全面的学习[21]。

（1）准确性

在实际应用中，可以通过答题准确性（accuracy）评估习题难度。如式（21）所示，表示学生对所推荐习题的作答结果（正确为1，不正确为0），表示在推荐的n道习题中学生作答正确的题数，做对题数除以总题数表示答对概率，通过判断答对概率与设定值δ（在实验中，该值为0.7）的接近程度来衡量推荐效果，越接近则推荐效果越好。

（2）新颖性

第2个指标为习题新颖性（Novelty）[22]，若推荐习题中包含越多学生未答或答错知识点，则推荐的习题新颖性越高。在介绍新颖性计算式之前先了解一下Jaccar2系数的概念，Jaccar2相似系数[23]用于比较有限样本集之间的相似性与差异性，系数值越大，样本相似度越高。下列计算式中e (ki)==1表示习题e (k)包含第i个知识点，E (k)表示习题e( k)包含的所有知识概念；相对的E (k)r表示正确回答的习题e (k)r包含的知识点；为Jaccar2 距离的计算式，表示未答或答错知识点占所有知识点的比重，通过对推荐习题列表中的每一道题进行Jaccar2距离加权平均值计算就可以得到推荐习题的新颖性值。

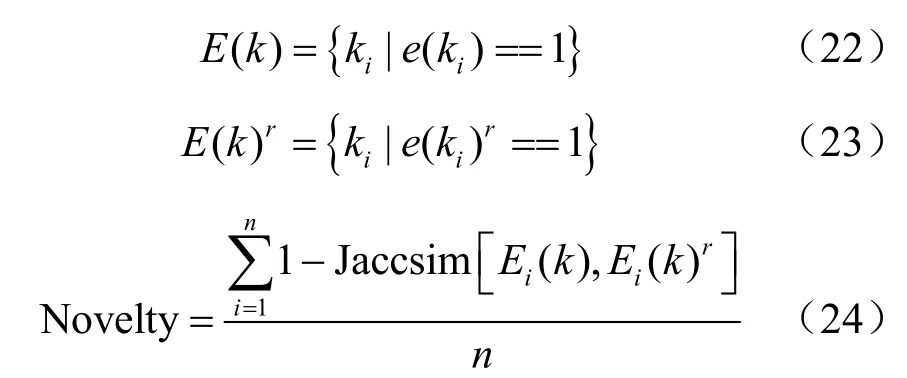
（3）多样性 第3个指标为习题多样性（Diversity），多样性表示推荐练习所包含知识点间的差异，用两个习题的知识点向量之间的余弦相似度进行定量表示[24]。首先计算推荐列表中每道题之间的知识点差异度，再对推荐的n道题进行差异度均值计算得到多样性值，计算式如下：

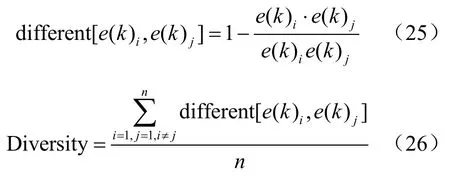
3.4 实验及结果分析

3.4.1 实验环境

实验环境操作系统为 Bin2ows10 64 bit，语言为Python3.6，采用PyTorch1.8.1版本，GPU型号为RTX 2080 Ti。

3.4.2 模型参数设置

在DKVMN模型训练阶段，学习速率和迭代次数设置为0.005和50，使用 A2am 优化算法，使用 Glorot初始化所有可训练的参数[25]。对于模型批尺寸（batchsize）的设置，通过在测试数据集上的平均AUC得分来确定，AUC的值越大表明模型的性能越强，不同批尺寸下AUC值对比结果见表2。ASSIST2009和DouDouYun数据集的批尺寸为32时，AUC值最高；STATICS数据集的批尺寸为8时，AUC值最高，这是由于该数据集缺乏随机噪声引起的。通过模型在测试数据集上的平均AUC得分来确定知识点嵌入向量的维度kd和学生知识掌握程度嵌入向量的维度vd的超参数设置。为了减少参数数量，一般设

3.4.3 模型预测性能对比分析

实验采用五重交叉验证的形式，每轮将数据集随机分成两份，其中70%作为模型的训练数据，10%作为验证数据，剩余20%的数据集用作整个推荐模型的测试数据。为了度量DKVMN算法的性能并与现有知识追踪模型——贝叶斯知识追踪（Bayesian knowle2ge tracking，BKT）、DKT进行比较，本文采用知识追踪领域的标准度量AUC（曲线下面积）、ACC（准确率）、RMSE（均方根误差）作为性能衡量指标，AUC和ACC的值越大表明模型的预测性能越强，RMSE的值越小表明模型的预测性能越好。模型预测性能对比见表3，给出了DKVMN与另外两个模型在3个数据集的平均AUC 值、平均 ACC 值和平均 RMSE 值的对比结果。表3表明DKVMN在3个数据集上的平均AUC、ACC、RMSE都优于另外两种知识追踪模型，这也证明了DKVMN在预测学生答题表现上性能优于现有模型。BKT在3个模型中性能最低，这表明对学生的知识掌握状态直接二值化是有缺陷的。DKT的预测性能也低于DKVMN，这是因为其使用RNN虽然能够获得学生整体的知识水平状态，却无法准确预测对某个知识点的掌握水平。可以看到在不同的数据集上模型的精确度不同且差异较大，这与数据集中包含的题库类别、单位学生做题数及单位习题包含知识概念数息息相关。随着预测精度的提高，推荐模型可以更好地确保推荐的效果，因此采用上述训练得到的最优模型进行组合得到本文提出的SKT-MIER习题推荐模型。

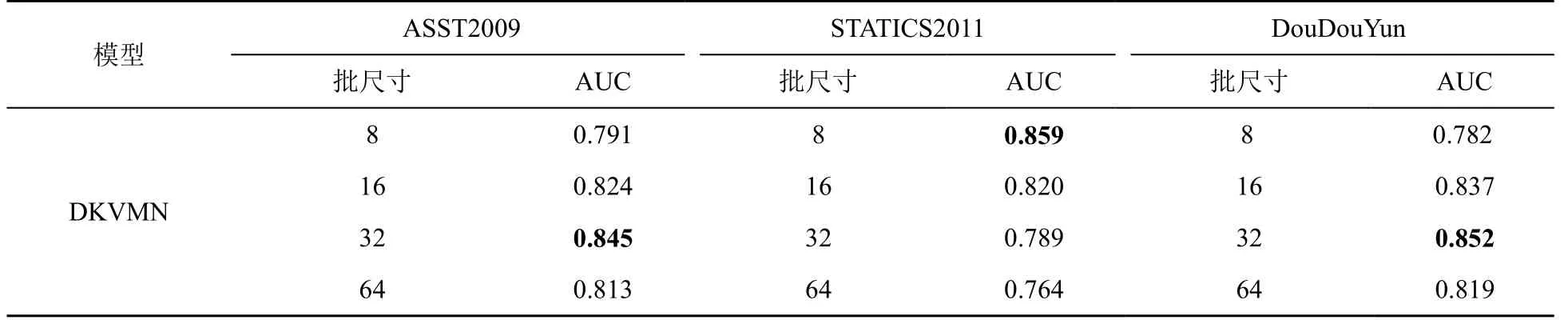
表2 不同批尺寸下AUC值对比结果

表3 模型预测性能对比

3.4.4 实验结果

为了比较各习题推荐模型的效果，实验使用上文提到的4个数据集，其中20%的学生数据用于测试推荐系统的效果。首先将这20%的学生做题记录输入SF-KCCP模型，得到学生知识点学习范围向量，根据范围向量得到预备习题库。在习题再过滤阶段，根据设置的期望难度iδ和预测难度ig之间的距离对预备习题库进行重排序，选择前n道习题进行推荐。

习题推荐的准确性见表4，习题推荐多样性见表5，习题推荐的新颖性见表6，分别展示了上述4种模型在推题准确性、新颖性和多样性上的结果。Mean值表示推荐列表中相应指标的平均值，该值越接近1，性能越好。St2.D表示各指标的标准差，该值越接近0，推荐效果越稳定。

表4反映了4种模型在4个数据集上推荐习题的准确性，SKT-MIER模型相较其他3种模型的推题准确度是最高的。在DouDouYun数据集中，模型DKT-CF的稳定性略优于本文所提模型，这是由于该数据集学生数较多，且SKT-MIER在计算学生i的平均知识掌握水平ig时，需要考虑相似学生的知识掌握水平。这里设置了较大的相似学生的权重系数ρ，所以推荐的稳定性受到影响。

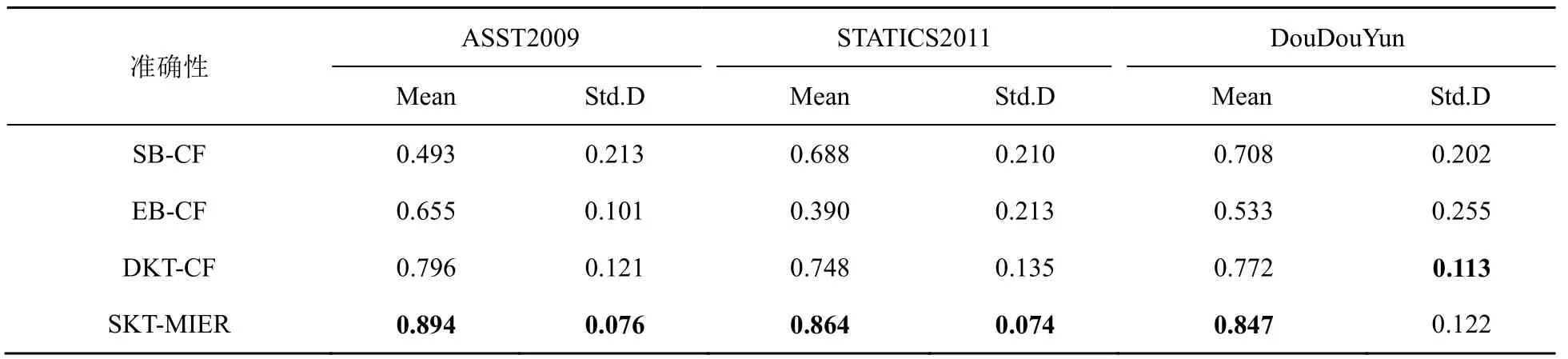
表4 习题推荐的准确性

表5 习题推荐的多样性

表6 习题推荐的新颖性

表5反映了4种模型在不同数据集推荐习题多样性上的差异，可以发现，当数据集的知识概念较少时，生成的推荐习题集的多样性也会降低。在ASST2009数据集中，模型DKT-CF的稳定性略优于本文所提模型，此处与表4的原因相同，因为SKT-MIER设置了较大的相似学生的权重系数ρ，所以推荐的稳定性受到影响。

表6反映了4种模型在3个数据集上推荐习题新颖性上的差异，习题数量越多则习题的新颖性越高。

习题推荐准确性如图8所示，习题推荐多样性如图9所示，习题推荐新颖性如图10所示，图8～图10中不同的折线表示不同模型在推题准确性、多样性和新颖性上的结果，横坐标为推题组数，每组推荐10道题。

从图8的实验结果可知，传统的习题推荐算法SB-CF和EB-CF在推荐的准确性上比较差，而DKT-CF和SKT-MIER模型的推题准确性有显著的提高，这证明了DKT在提高推荐准确性上的有效性。SKT-MIER采用了基于增强神经网络的DKVMN知识追踪网络，可以更精准地挖掘学生的知识掌握水平，所以习题推荐的准确性明显优于其他3个模型。

习题推荐多样性如图9所示。值得注意的是本文提出的SKT-MIER模型在3个数据集的多样性结果比DKT-CF模型平均高出8.7%，这是因为本文采用了学生知识点学习范围向量和学生知识掌握水平向量作为双重指标判定相似学生，可选学生范围更广，可供推荐的知识点更加多元，所以推荐的习题更加多样化。

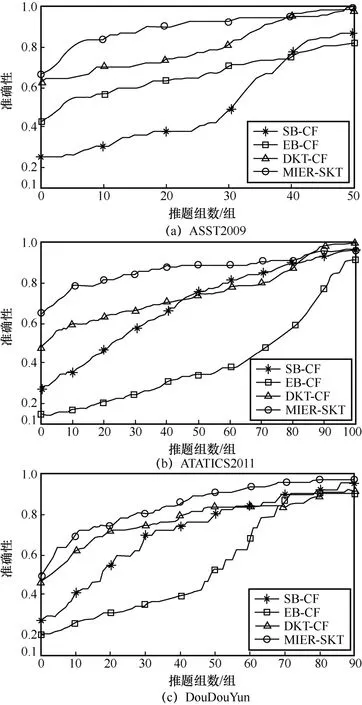
图8 习题推荐准确性

习题推荐新颖性如图10所示，显示了SKT-MIER模型在推题新颖性方面有较好的表现。传统推荐算法忽略了学习中的遗忘特性，在不断推题过程中无法根据学生知识掌握情况的改变而变化，导致推题的新颖性不足。学生的遗忘行为会导致先前学过的知识点在一定程度上转变为未学知识点，因此本文在SKT-MIER中融入了学生的遗忘规律，使推荐习题中包含更多未学或遗忘的知识点，所以在推题新颖性上优于传统模型。综上所述，本文所提方法比其他3种基线模型有明显的优势。

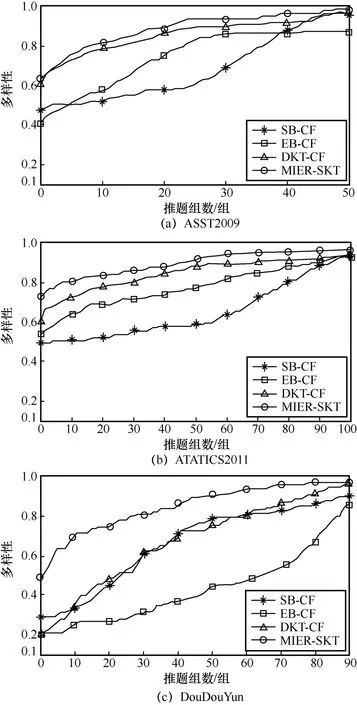
图9 习题推荐多样性

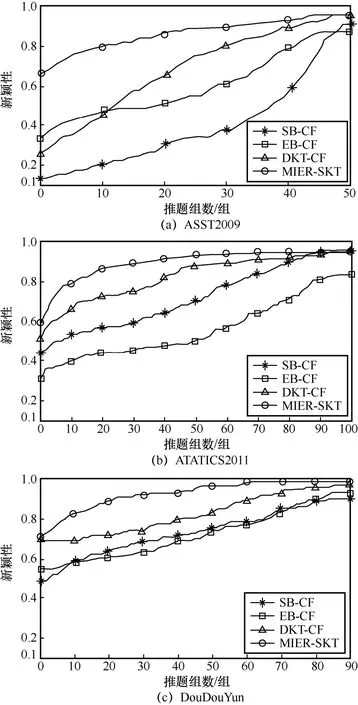
图10 习题推荐新颖性

4 结束语

针对传统的习题推荐算法忽略了学生的遗忘规律，不能合理地将学生知识掌握水平与相似学生的共性特征进行结合，推荐习题的评价指标单一，新颖性和多样性不足，不能合理地促进学生对新知识的学习或帮助学生查缺补漏等问题，本文结合深度知识追踪模型和基于用户的协同过滤算法，提出一种基于学生知识追踪的多指标习题推荐方法。该方法首先从学生已经学习的知识点范围出发，提出了基于学生遗忘规律的知识点学习范围预测模型，从而满足习题推荐新颖性，合理地促进学生学习新知识；然后从学生对知识点的掌握程度出发，利用DKVMN模型追踪学生的知识掌握水平，从而实现习题的个性化精准推荐，合理地激发学生的学习热情；最后从学生群体之间的相似性出发，将UserCF算法融入再过滤模块，实现推荐习题的多样性，合理地帮助学生查缺补漏。最后本文作者团队在几个经典教育数据集上验证了SKT-MIER方法的优势，证实了该方法的有效性及合理性。

虽然本文提出的习题推荐模型优于多个现有方法，但仍有许多可以改进的地方，在未来可以朝以下几个方向深入研究。

（1）对题目文本进行语义分析

建立学生行为和习题内容之间的语义联系，进一步解决推荐时的冷启动[27]问题。

（2）进行多类型习题推荐研究

前大多数模型的研究以选择题居多，答题结果也只有对或错两类，在实际情况中习题类型丰富多样，有选择填空、问答以及计算题等，答题结果并非只有0和1的情况，对于多样化的习题类型，知识图谱[28]技术会是一个不错的选择。

（3）提高推荐算法的效率

为了充分挖掘学生行为数据，实现精细化推荐，本文研究极大地提高了算法复杂度，在未来可采用更先进的模型或优化流程简化模型复杂度，实现快速推荐。

（4）探索知识追踪多场景应用

在实际学习中除了习题、知识点、答题结果等数据，还有如做题尝试次数、题目解析查看情况以及题目收藏情况等标签，当前对于这些标签的使用场景研究还不够深入，未来可持续探索。