考虑黏聚力与内摩擦角的变坡面浅埋偏压隧道围岩压力计算方法
2022-10-09杜建明房倩
杜建明,房倩
(隧道及地下工程教育部工程研究中心(北京交通大学),北京 100044)
偏压隧道是指由于地形条件不对称或者地质岩层差异等因素导致结构承受显著偏压荷载的隧道[1].相比于无偏压隧道,偏压隧道结构受力更复杂、施工风险更高,如隧道结构设计或施工方案不合理,则极易诱发安全事故,尤其在埋深较浅的洞口段.因为围岩压力的合理计算是浅埋偏压隧道结构设计与施工方案编制的基础,所以对浅埋偏压隧道围岩压力计算方法开展深入研究具有重要的科学价值与工程意义.
目前,众多学者通过现场实测[2-4]、模型试验[5-9]、数值计算[10-11]以及理论分析[12-16]等手段对浅埋偏压隧道围岩压力分布特征以及计算方法进行了系统研究.在现场实测方面,高杰[2]通过对鹤大高速公路回头沟隧道围岩压力分布特征进行持续现场监测,分析了偏压隧道围岩压力的动态演化过程.苏运基[4]对贵州黔春大道七冲村二号浅埋偏压隧道围岩压力变化规律进行了现场监测,分析了浅埋偏压大跨度隧道围岩压力的分布特性.在模型试验方面,雷明峰等[5-6]利用室内相似物理模型试验对地表偏压角对浅埋偏压隧道围岩压力的影响规律进行了系统研究.辛毓龙[7]根据相似物理模型试验对不同地形偏压条件下围岩压力分布特征进行了研究分析,并利用隧道各对称位置的围岩径向应力定义偏压系数来衡量隧道的偏压程度,通过大量物理模型试验给出了地形偏压隧道偏压程度判定表.在数值计算方面,王传智[10]利用有限差分数值软件对十堰至天水联络线高速公路新安岭隧道不同施工工法下围岩压力分布特点进行了数值分析.李建鹏[11]通过数值计算对三种不同施工工法(单侧壁导坑法、三台阶临时仰拱法以及交叉中隔壁法)下浅埋偏压隧道围岩压力分布特性进行了研究分析.在理论分析方面,邱业建等[12]结合模型试验结果与相关联流动法则,构建了浅埋偏压隧道破坏模型及其对应的速度场,然后根据虚功原理推导出浅埋偏压隧道围岩压力的极限上限解.严涛等[13]运用极限平衡法推导了邻路基变坡条件下浅埋偏压隧道围岩压力解析解.张治国等[14-15]采用拟静力法,通过极限受力分析,在考虑水平地震力与竖向地震力的综合作用后,将岩土体黏聚力作为独立参数进行考虑,进而得出地震作用力下考虑黏聚力的浅埋偏压隧道围岩压力解析解.上述研究成果极大地丰富了浅埋偏压隧道围岩压力分布特征及计算方法的研究内容.
然而,这些研究内容均假设隧道拱顶地表为一条斜直面,这种假设与现实中不规则变坡面的地形地质条件存在一定差异.为此,刘翔等[16]基于极限平衡法提出了变坡面条件下浅埋偏压隧道松动围岩压力的计算方法,并分析了地表坡度变化对水平侧压力系数的影响规律.但是,刘翔等[16]所提方法未对黏聚力及内摩擦角影响下水平侧压力系数的变化规律进行深入研究,也未把黏聚力与内摩擦角作为独立参数进行公式推导,从而使得其所提方法不能对环境变化引起岩土体黏聚力突变时围岩压力的变化规律进行研究,导致该方法应用依然存在一定的局限性.
为此,本文基于极限平衡法原理,在公式推导过程中加入黏聚力与内摩擦角分算方法,从而将岩土体黏聚力与内摩擦角转变为独立变量,进而得出独立考虑黏聚力与内摩擦角的变坡面浅埋偏压隧道围岩压力计算方法;然后,通过与规范和刘翔等[16]所提方法进行对比分析验证了本文所提方法的合理性;最后,利用算例分析变坡面浅埋偏压隧道深埋侧水平侧压力系数的影响因素.
1 围岩压力计算公式推导
1.1 计算模型
图1 为考虑黏聚力与内摩擦角的变坡面浅埋偏压隧道围岩压力荷载计算示意图.为了便于后文计算公式推导,将围岩压力计算模型简化为平面应变问题,现取纵向长度1 m 的隧道作为研究对象,从而将三维模型转化为二维模型进行研究.其中,EFG1Gn为不规则变坡面的地面线型;AF(浅埋)与BG1(深埋)分别为隧道两侧底部距地面的埋深;CF与DG1所在平面为隧道两侧楔形体(AFE与BG1Gn)与隧道拱顶上覆岩土体(CDG1F)之间的接触平面;AE与BGn所在平面为隧道两侧楔形体(AFE与BG1Gn)假定滑动破裂面.

图1 围岩压力荷载计算示意图Fig.1 Sketch of load calculation diagram for surrounding rock pressure
1.2 计算假设
为了便于后文计算公式推导,进行如下假设:
1)隧道周边岩土体为均匀连续、各向同性体,且服从摩尔-库伦屈服准则.选择隧道埋深大于等效荷载高度且小于等效荷载高度(2.0~2.5)倍作为隧道浅埋判定准则[17];
2)隧道拱顶上覆岩土体CDG1F下沉过程中,带动隧道两侧楔形体AFE与BG1Gn分别沿各自的假定破裂面AE与BGn滑动,与此同时,隧道两侧楔形体AFE与BG1Gn对拱顶上覆岩土体CDG1F施加阻力作用;
3)滑动破裂面为平面,破裂角β=45°+φ/2,且浅埋情况下滑动破裂面能够发展至地表.
1.3 计算公式
1.3.1 隧道周边岩土体自重
图2 为隧道右侧楔形体BG1Gn截面示意图.其中,G1、G2、G3、…、Gi、…、Gn依次为变坡面G1Gn段变坡点;α1、α2、α3、…、αi、…、αn依次为变坡面G1Gn段与水平面之间的坡角(地面);δ1、δ2、δ3、…、δi依次为变坡面G1Gn段相邻变坡点与隧道右侧底角B点连线的夹角(岩土体).当楔形体位于隧道右侧时,夹角δi为正值;反之,当楔形体位于隧道左侧时,夹角δi为负值.其中,W表示隧道顶部四棱体CDG1F自重,W1表示隧道左侧楔形体AFE自重,W2表示隧道右侧楔形体BG1Gn自重.由图2可得:

图2 右侧楔形体截面示意图Fig.2 Sketch of cross section of right wedge
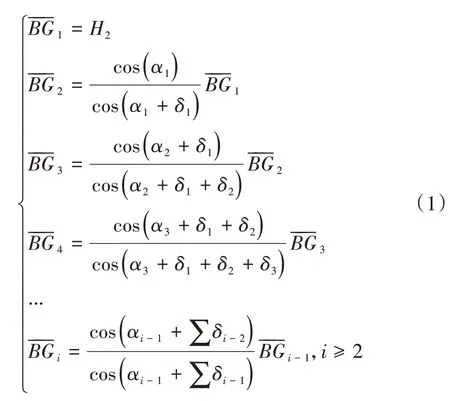
右侧楔形体BG1Gn截面积Sr的计算公式可表示为:
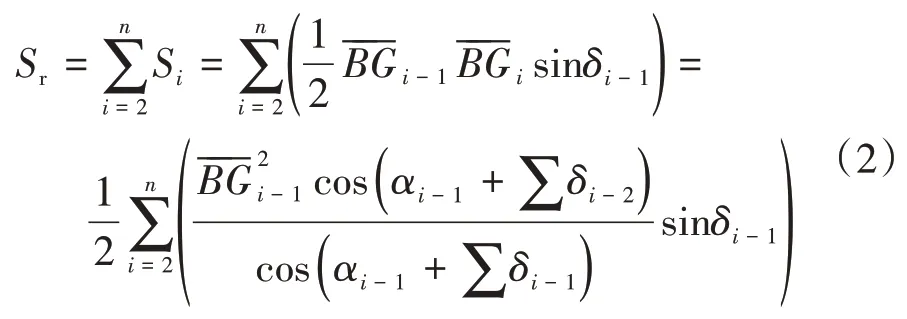
右侧楔形体BG1Gn自重W2的计算公式可表示为:

令αi和δi的函数为K2,即K2的表达式可表示为:
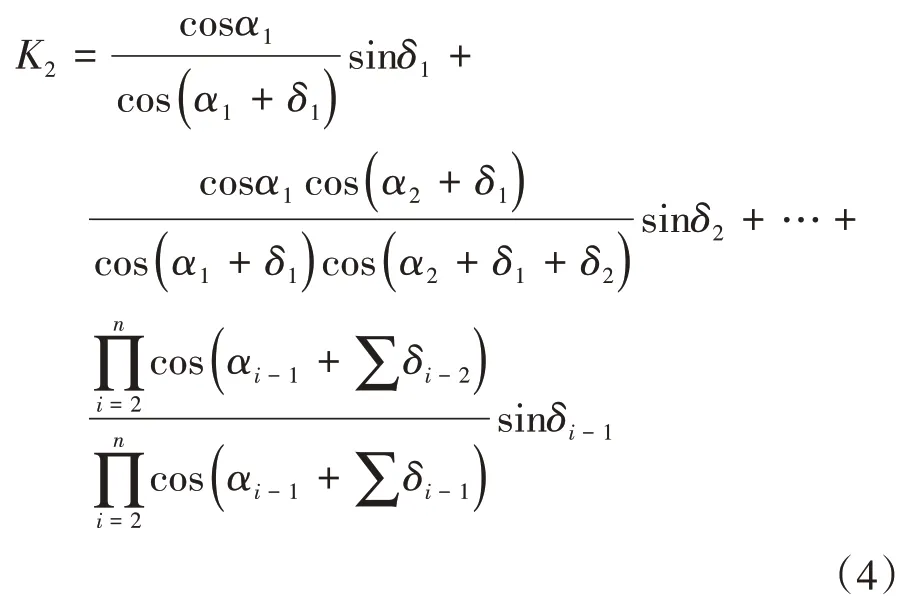
则右侧楔形体BG1Gn自重W2的计算公式可简化表示为:

式中:γ为岩土体重度.
同理可求得左侧楔形体AFE自重W1的计算公式与右侧楔形体BG1Gn自重W2的计算公式相同,只是左侧变坡面处夹角δi为负值,因为左侧与右侧楔形体截面示意图形式相反.
图3 为隧道顶部四棱体CDG1F截面示意图.参数Fi和α1i含义与图2中Gi和αi相类似.由图3可知,
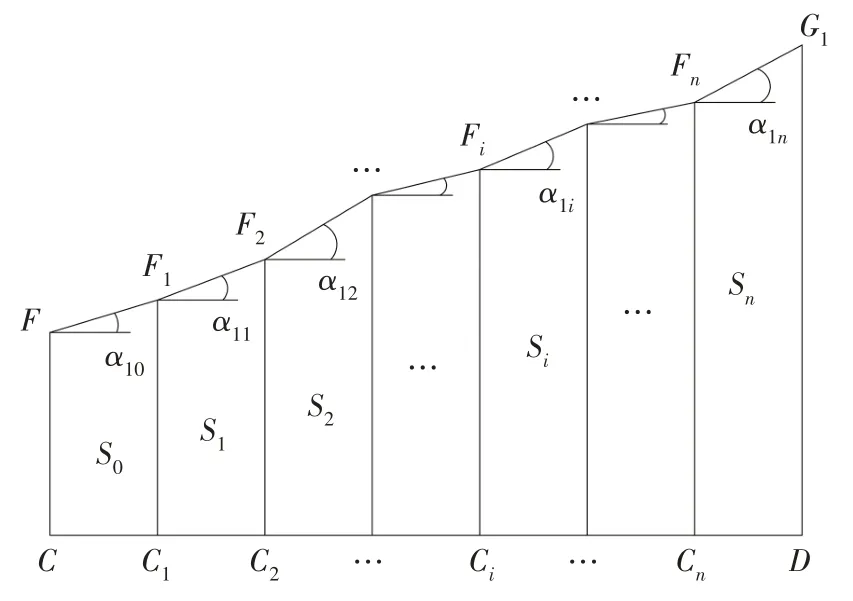
图3 四棱体CDG1F截面示意图Fig.3 Sketch of cross section of quadrangular CDG1F
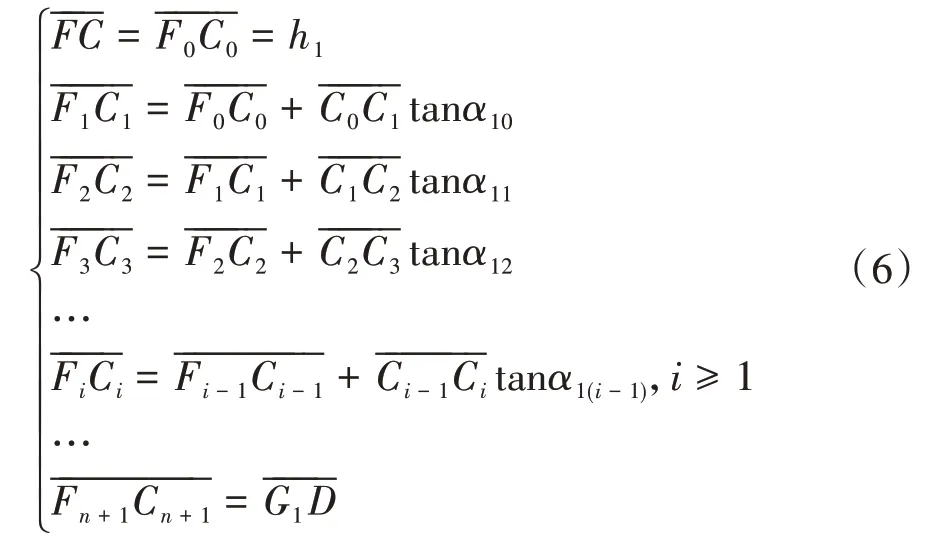
各分块面积的计算公式可表示为:
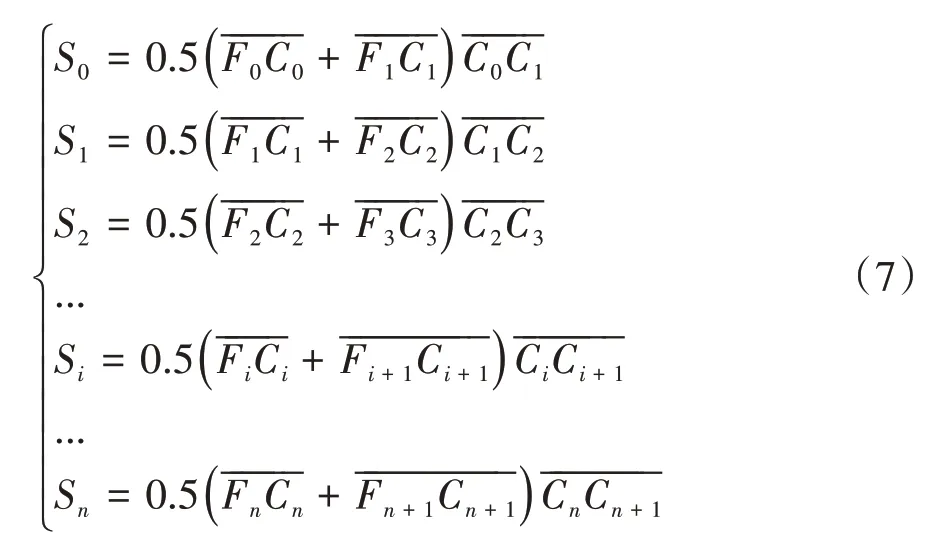
隧道顶部四棱体CDG1F截面积St的计算公式可表示为:

隧道顶部四棱体CDG1F自重W的计算公式可简化表示为:

1.3.2 隧道两侧楔形体推力
图4 为隧道右侧楔形体BG1Gn受力分析示意图,取水平方向为X轴,竖直方向为Y轴.其中,W2为楔形体BG1Gn自重;T2与τ21分别为隧道拱顶岩土体下沉时施加在楔形体BG1Gn上的推力与抗剪力,且τ21=c1H2;F2与τ22分别为右侧滑动破裂面BGn下部静止岩土体施加在楔形体BG1Gn上的摩擦阻力与抗剪力,且τ22=c2L2;q与P分别为作用在隧道拱顶地表的均布荷载与集中荷载,令F0=qd0+P,d0为楔形体BG1Gn上侧G1Gn边的水平距离;c1与c2分别为楔形体BG1Gn左侧与右侧黏聚力;θ与φ分别为楔形体BG1Gn左侧与右侧内摩擦角;L2为楔形体BG1Gn右侧BGn边长度.因为面BGn为假定滑动破裂面,而面BG1为非假定滑动破裂面,所以面BG1上的滑动阻力要小于面BGn,故假设:
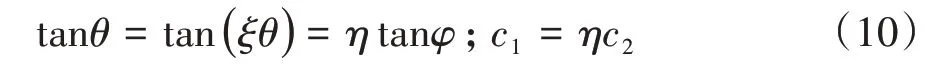
式中:ξ的取值参考文献[18];η为比例系数,且0<η<1.
根据图4中楔形体受力平衡,可得:
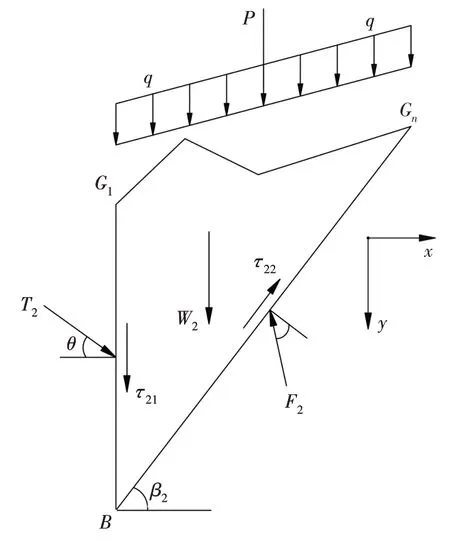
图4 右侧楔形体受力示意图Fig.4 Sketch of force analysis of right wedge
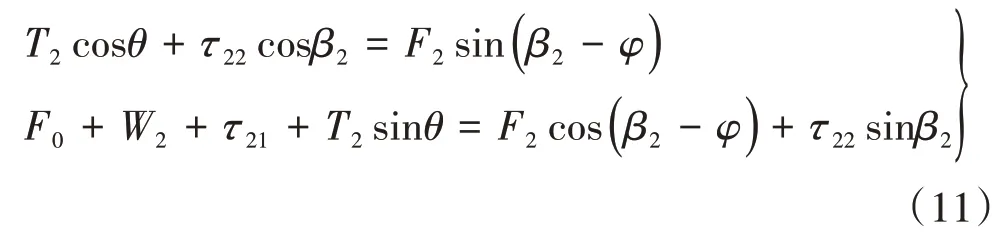
由式(11)可得:

其中:

式中:λ2为隧道右侧水平侧压力系数.
同理可求得左侧楔形体AFE所受推力T1与水平侧压力系数λ1的计算公式与右侧楔形体相同,只是左侧变坡面处夹角δi为负值,因为左侧与右侧楔形体截面示意图形式相反.根据普氏理论[19],可假设滑动破裂角β=45+φ/2.根据公式(12)可分别求出隧道右侧与左侧所提供的推力T2与T1,进而就可对隧道周边围岩压力进行求解.
1.3.3 隧道周边围岩压力
图5 为隧道顶部四棱体CDG1F受力分析示意图.T′1与T′2分别为隧道两侧岩土体施加在隧道顶部四棱体CDG1F上的推力;τ′11与τ′21分别为隧道两侧岩土体施加在隧道顶部四棱体CDG1F上的抗剪力,其余符号意义同前.由图5 可知,隧道拱顶围岩压力Q的计算公式可表示为:
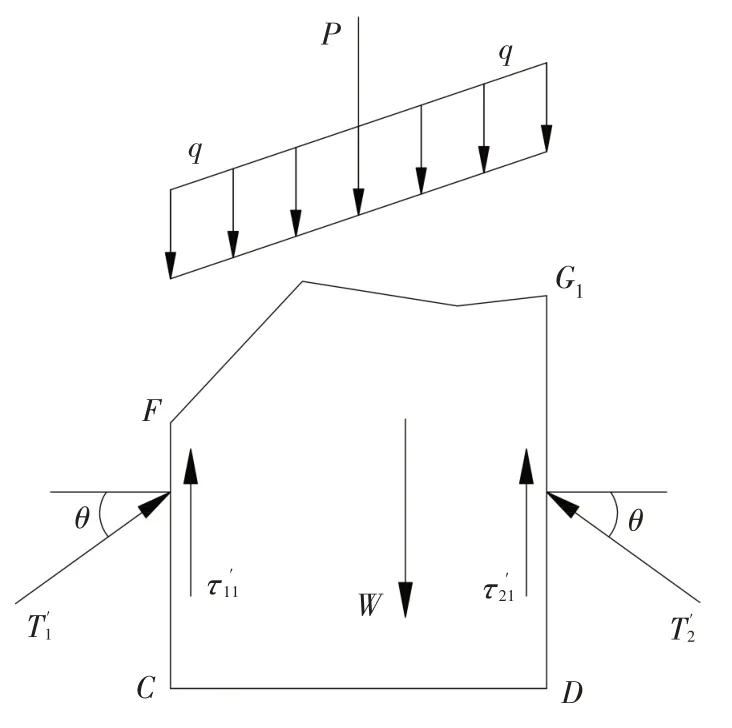
图5 四棱体CDG1F受力示意图Fig.5 Sketch of force analysis of quadrangular CDG1F
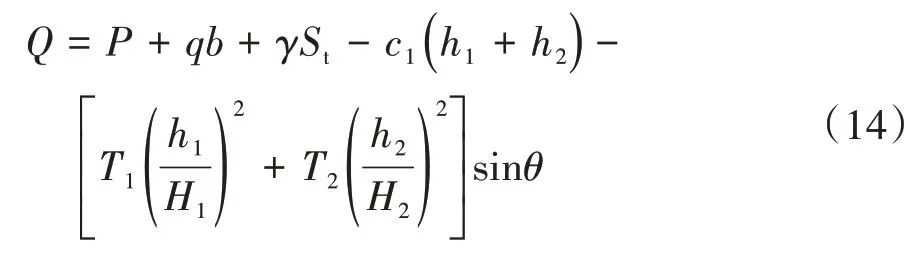
右侧水平侧压力的计算公式可表示为:

同理可求得左侧水平侧压力e11、e12的计算公式与右侧e21、e22相同,原因同前.故只需将右侧水平侧压力计算公式中的参数λ2、h2和H2替换为左侧水平侧压力系数计算参数λ1、h1和H1即可.
2 对比与验证
如果令c1=c2=c,即比例系数η=1,则式(12)与式(13)的简化形式与刘翔等[16]所推公式形式相同.进一步假设岩土体黏聚力为零(令c1=0,c2=0),拱顶地面集中荷载与均布荷载为零(令P=0,q=0),拱顶地面为一个斜直线时(令α1=α2=αi=αn=0),当采用计算内摩擦角代替摩擦角时(φ=φc,θ=θc),则式(4)可简化为:
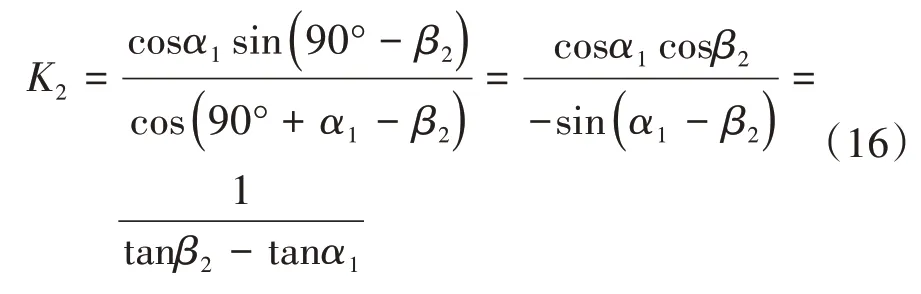
同时可将式(13)简化为:

简化后的式(17)与规范公式相同[17].因此,刘翔等[16]方法与规范方法实际上都可看成是文章的一个特例.
为了进一步验证文章所推公式的合理性及准确性,现通过一个简单算例对文章计算结果与刘翔等[16]方法计算结果进行对比分析.所用算例参数如下:隧道几何参数取b=15 m,h=10 m,h1=12 m,h2=18 m,α1=30°,α2=30°;力学参数参考文献[20]取值如表1 所示,破裂角β2=45°+φ/2,则δ1+δ2=90°-β2=45°-φ/2.采用文章分开考虑黏聚力c2与内摩擦角φ的计算方法与刘翔等[16]未分开考虑的计算方法进行对比分析,计算所得隧道深埋侧水平侧压力系数λ2与推力T2,如表2 所示.可知,文章计算方法所得水平侧压力系数λ2比刘翔等[16]方法计算所得结果小0.08~0.14,推力T2比其小0.21~7.80 MPa;在围岩等级较低时,如IV 级围岩,文章计算方法与刘翔等[16]方法计算所得结果较为相近,λ2的差异仅为0.08,T2的差异仅为3.1%;随着围岩级别提高,两者误差逐渐增大,文章计算结果显著低于刘翔等[16]方法计算所得结果,其主要原因是文章计算方法中将黏聚力c2与内摩擦角φ两个力学参数作为独立变量进行考虑.需要说明的是,λ2与T2存在差异还可能受夹角δ1与δ2取值影响.
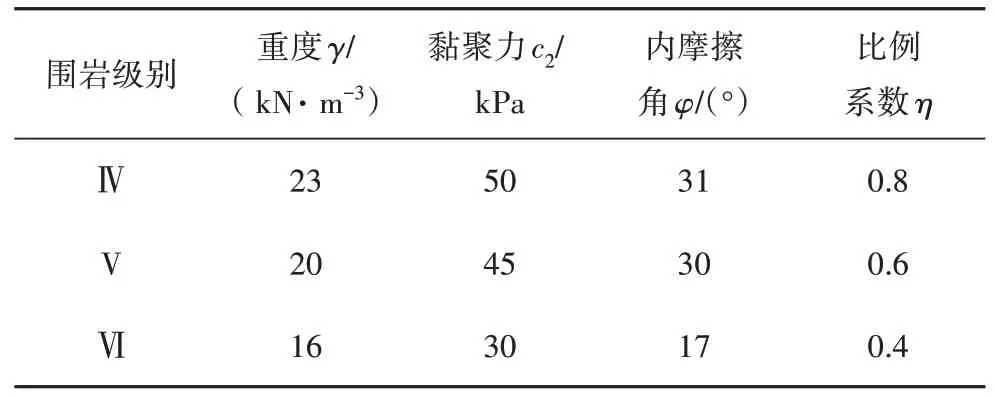
表1 岩土体力学参数Tab.1 Mechanical parameter of rock/soil mass
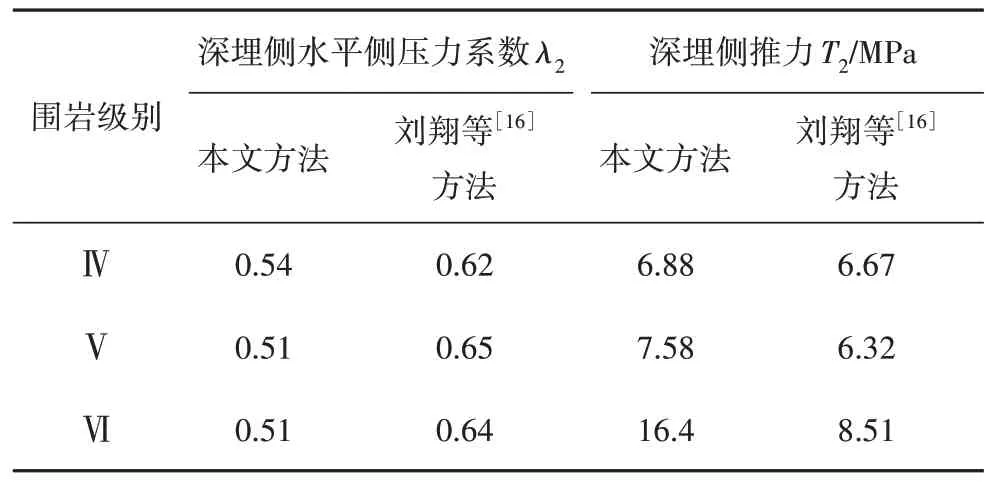
表2 文章方法与刘翔等[16]公式计算结果对比Tab.2 Calculated results comparison of paper and the formula of Liu et al[16]
通过与规范法或基于规范法的计算公式对比可知,文章推导的水平侧压力系数(式(13))相当于对规范计算公式进行了综合修正,即通过参数P与q来考虑隧道拱顶地面集中荷载与均布荷载的影响;通过参数c1/θ与c2/φ将黏聚力和内摩擦角作为独立因素来考虑,能够更为准确地计算浅埋隧道围岩压力[20],同时还可以考虑环境因素(如降雨等)影响下黏聚力急剧变化带来的影响;通过参数K来考虑隧道拱顶地面为变坡面的情况,因为K是隧道拱顶地面变坡段与水平面之间夹角αi以及相邻变坡点与隧道底角A/B点连线夹角δi的函数.因此,文章所推公式比规范法或基于规范法的计算公式更能反映变坡面浅埋偏压隧道围岩压力分布特征的真实情况.
3 水平侧压力系数敏感性分析
水平侧压力系数与围岩压力密切相关,当水平侧压力系数增加时,隧道两侧岩土体对拱顶上覆岩土体施加的推力增大,水平侧压力随之增大,拱顶围岩压力随之减小;反之亦然.所以水平侧压力系数的变化趋势在一定程度上能够反映围岩压力的变化规律,故对水平侧压力系数的影响因素进行敏感性分析.
假设隧道拱顶地面集中荷载P与均布荷载q均不存在,即P=0,q=0,结合式(10)对式(13)进行分析可知,影响隧道右侧水平侧压力系数λ2的因素主要是假定滑动破裂面BGn上的内摩擦角φ以及黏聚力c2、参数K2,而影响参数K2的因素主要是坡角αi与夹角δi,故内摩擦角φ、黏聚力c2、坡角αi以及夹角δi对水平侧压力系数λ2产生影响.假设隧道右侧存在2个变坡面时,即坡角αi与夹角δi只有α1、α2与δ1、δ2的情况进行研究分析.隧道几何参数、围岩力学参数取值同第2 节中简单算例取值,围岩级别选择Ⅴ级围岩.
3.1 坡角αi敏感性分析
令坡角α2分别取5°、10°、15°、20°、25°以及30°,计算并绘制隧道右侧水平侧压力系数λ2分别随坡角α1变化的影响规律曲线,如图6 所示.可知,水平侧压力系数λ2随坡角α1的增加呈现出逐渐增大的趋势、以α2=10°为例,当坡角α1由5°增加至30°时,水平侧压力系数λ2由0.406 0 增加至0.459 9,增幅达13.28%;以α1=10°为例,当坡角α2由5°增加至30°时,水平侧压力系数λ2由0.404 3 增加至0.459 9,增幅达13.75%,表明在参数取值相同的情况下,坡角α2对水平侧压力系数λ2的影响程度要略大于坡角α1,其主要原因是坡角α2所影响的岩土体范围较大.
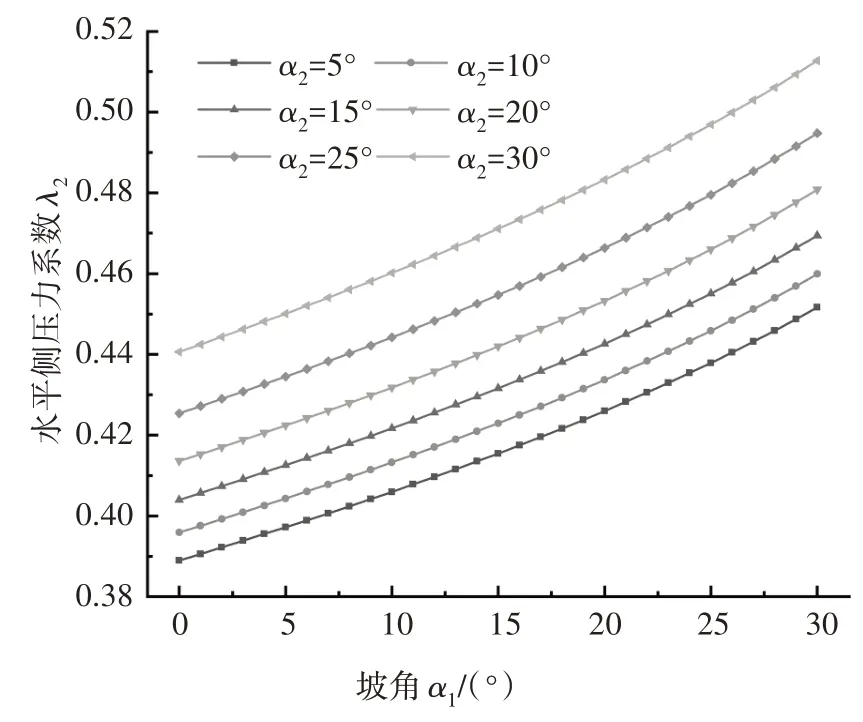
图6 坡角αi敏感性分析Fig.6 Sensitivity analysis for slope αi
3.2 夹角δi敏感性分析
令坡角α1/α2分别取5°、10°、15°、20°、25°以及30°,计算并绘制隧道右侧水平侧压力系数λ2随夹角δ1变化的影响规律曲线,如图7所示.可知,水平侧压力系数λ2随夹角δ1的增加(δ1+δ2为定值)呈现出先减小后增大的二次型变化趋势.当夹角δ1为定值时,水平侧压力系数λ2随着坡角α1/α2的增大而增大(除δ1=0°/30°);当δ1=0°、δ2=30°,δ1=30°、δ2=0°时,地表变坡面无变坡点,简化为一个斜直面,故δ1=0°/30°时,水平侧压力系数λ2为一定值.
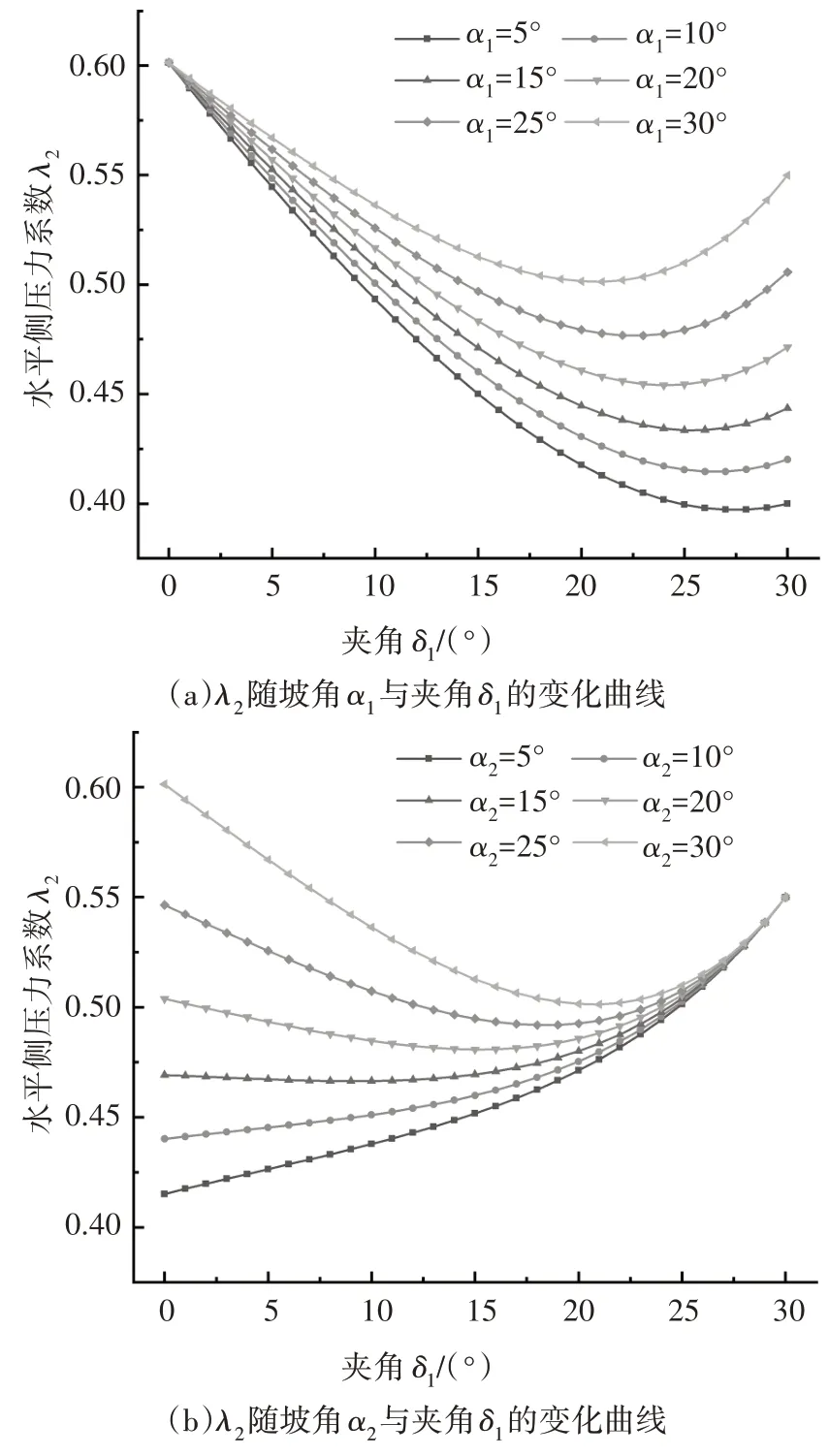
图7 夹角δi敏感性分析Fig.7 Sensitivity analysis for angle δi
3.3 内摩擦角φ敏感性分析
令坡角α1分别取5°、10°、15°、20°、25°以及30°,计算并绘制隧道右侧水平侧压力系数λ2随内摩擦角φ变化的影响规律曲线,如图8所示.可知,水平侧压力系数λ2与内摩擦角φ呈现线性负相关性,即水平侧压力系数λ2随内摩擦角φ的增大逐渐减小,以α1=15°为例,当内摩擦角φ由0°增加至30°时,水平侧压力系数λ2由1.332 8 减小至0.469 4,降幅达66.48%,表明内摩擦角φ对水平侧压力系数λ2影响较大.
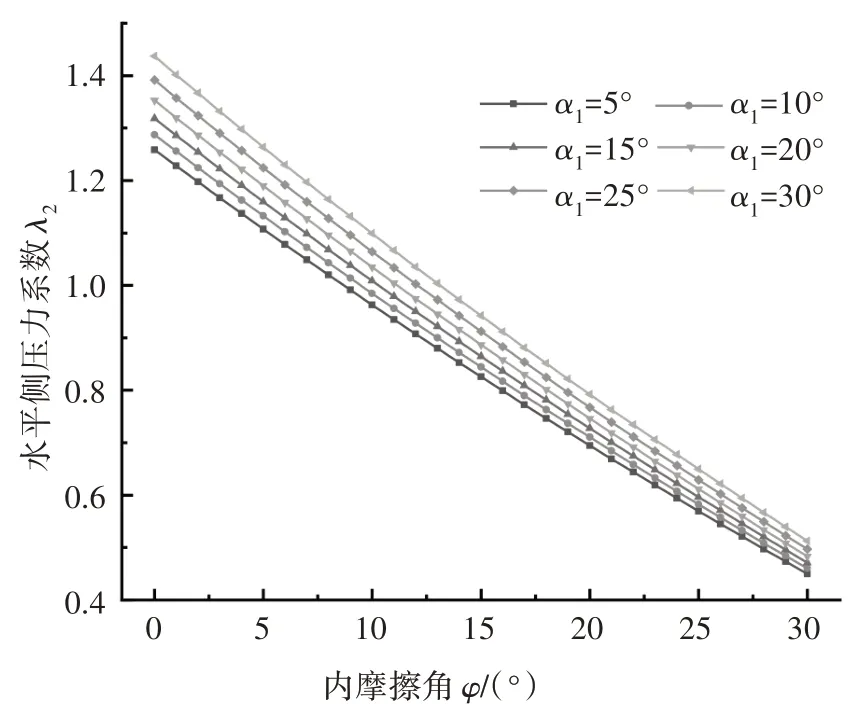
图8 内摩擦角φ敏感性分析Fig.8 Sensitivity analysis for internal friction angle φ
3.4 黏聚力c2敏感性分析
令坡角α1分别取5°、10°、15°、20°、25°以及30°,计算并绘制隧道右侧水平侧压力系数λ2随黏聚力c2变化的影响规律曲线,如图9 所示.可知,水平侧压力系数λ2与黏聚力c2呈现线性负相关性,即水平侧压力系数λ2随黏聚力c2的增大逐渐减小.以α1=15°为例,当黏聚力c2由0 kPa 增加至30 kPa 时,水平侧压力系数λ2由0.503 0减小至0.471 1,降幅达6.34%,表明黏聚力c2对水平侧压力系数λ2影响较小.但是,将黏聚力作为独立参数能够有效考虑由于环境因素(如降雨)导致岩土体黏聚力变化带来的不利影响.
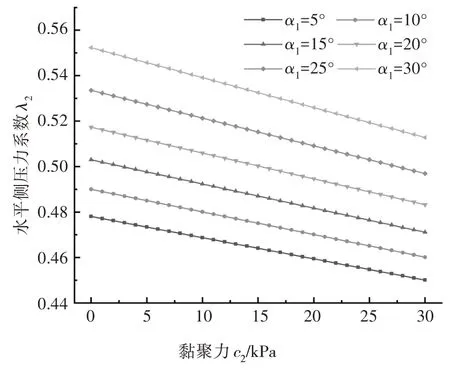
图9 黏聚力c2敏感性分析Fig.9 Sensitivity analysis for cohesion c2
4 结论
1)本文采用极限平衡法推导出变坡面情况下独立考虑黏聚力与内摩擦角的浅埋偏压隧道围岩压力计算方法.其中,黏聚力的分算有利于考虑环境因素(如降雨)引起的岩土体力学参数(黏聚力)急剧变化带来的不利影响,而内摩擦角对隧道深埋侧水平侧压力系数影响较大,表明将内摩擦角进行分算对围岩压力计算具有重要意义.
2)若令比例系数η=1.0,得到的公式与刘翔等[16]方法计算所得相同,进一步,若令滑动破裂面黏聚力c1=c2=0,滑动破裂面内摩擦角φ取计算内摩擦角φc,得到的公式与规范方法相同,表明刘翔等[16]方法与规范方法均可视为文章所提方法的一个特例.
3)通过算例分析坡角αi、夹角δi、黏聚力c2以及内摩擦角φ对隧道深埋侧水平侧压力系数λ2的影响规律.水平侧压力系数λ2随坡角αi的增加逐渐增大,随夹角δi的增加呈现先减小后增加的二次型变化,随黏聚力c2与内摩擦角φ的增加逐渐减小.
