多孔介质曲折度对膨润土衬垫渗透性能的影响

侯娟，滕宇阳，李昊，刘磊

（1.上海大学力学与工程科学学院，上海 200444；2.弗吉尼亚大学工学院，弗吉尼亚州夏洛茨维尔22904；3.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室，湖北武汉 430071）

膨润土衬垫（Geosynthetic Clay Liner，GCL）是由两层土工织物间夹裹一层薄的膨润土构成的，近几十年来广泛应用于垃圾填埋场的顶部封场及底部衬垫系统，具有防渗性能好、厚度小以及自愈力强等优点.目前对于GCL 渗透系数的研究，主要集中在宏、微观试验研究方面［1-2］，Shackelford 等［3］对GCL 进行了大量渗透试验，发现影响GCL 渗透性的因素有孔隙比、膨润土级配、厚度等.刘志彬等［4］对膨润土内部微孔隙进行了定量分析，并与扫描电镜图像进行了对比.王宝等［5］通过试验发现孔隙比与渗透系数存在良好的线性关系，该结论与Kang 等［6］用去离子水渗透GCL 结果相同.Mesri 和Olson［7］发现，渗透系数和孔隙比在对数坐标系下存在线性关系.Fratalocchi［8］研究了应力对GCL 渗透系数的影响，发现渗透系数的对数与孔隙比之间存在较好的线性关系，得到与Petrov 等［9］相似的结论.何俊等［10］通过微观结构分析，推导了GCL 的膨润土饱和渗透系数与孔隙比之间的计算公式.

然而，仅用孔隙率往往存在不能充分体现土体内部粒间孔隙特征等问题，也不能反映颗粒尺寸本身对渗透系数的影响［11］.自Kozeny［12］提出流径曲折度概念以来，Carman［13］考虑孔隙通道的不规则性，在Poiseuille 定律的基础上，结合Kozeny 公式得到了曲折度与渗透系数之间的表达式.Nooruddin 和Hossain［14］根据曲折度与土颗粒之间的关系，改进了Kozeny-Carman 模型.Tsang［15］研究了渗流路径的曲折度对流场的影响.Murata 等［16］基于孔隙介质的渗透系数Kozeny-Carman 方程，推导得到了修正的流量关系表达式.此外，还有众多学者采用试验研究［17］、理论分析［10，18］以及数值模拟［4］等手段研究了多孔介质孔隙流径的曲折度与孔隙率之间的关系.

GCL 中起主要防渗作用的膨润土，是一种颗粒遇水会膨胀的特殊多孔介质.然而，尽管目前已有大量研究表明GCL中膨润土孔隙率与渗透系数呈正相关的关系［19］，但是，如何从细观角度考虑膨润土颗粒尺寸及孔隙特征对GCL 渗透性能的影响，成为进一步研究和解释膨润土渗透机理的难点［9，20］.GCL 中曲折度是影响渗透系数的关键因素之一［21］，但对其膨胀过程中量化分析的研究比较鲜见，目前尤其缺乏对孔隙渗流通道的曲折度与孔隙率之间关系的研究.随着计算机技术的高速发展，数值模拟成为目前研究多孔介质曲折度的主要手段之一［22］.其中，COMSOL 在分析多物理场耦合以及在多孔介质中流体流动等复杂问题方面具有明显的优势［23］，因此，本文采用COMSOL 软件，构建了包含孔隙率与曲折度等细观变量的多孔介质GCL结构模型，从细观角度，研究土体的颗粒尺寸及孔隙特征等对GCL渗透性能的影响.首先，通过构建流体物理场和粒子追踪场，模拟分析蠕动流场的稳态速度图和压力矢量图，得到宏观流场分布规律；然后，通过对比宏观蠕动流场与微观流动（水）粒子分布规律，探究宏观流场分布与微观流动粒子之间的关系；同时，通过实时追踪液体粒子的运移过程，得到液体在多孔介质内流径并通过数学变换得到曲折度与流径曲折度的表达式；最后，采用毛管模型描述粒间孔隙组成的土骨架［24］，并基于此提出能够综合考虑孔隙率与流径曲折度的GCL渗透系数理论预测模型，验证模型的准确性.

1 模型建立和参数确定

COMSOL 以有限元为基础，通过求解偏微分方程（单场）和方程组（多场）实现多场耦合的仿真模拟［25］.建模的过程一般分为模型假设、确定物理场控制方程、几何模型建立、边界与初始条件确定、网格划分以及最终求解6个部分.

1.1 模型假设

参考张志红等［26］的研究，本文基本假设为：多孔介质内部为均一几何孔隙；过程等温；渗流液均质各向同性；忽略毛细管吸力作用；流体不可压缩且为单相稳定渗流.

1.2 物理场控制方程

1）流体物理场

由于GCL 的渗透系数较小，在膨润土粒间孔隙通道中，形成斯托克斯流（Stokes Flow），由Navier-Stokes连续性方程得蠕动流方程：

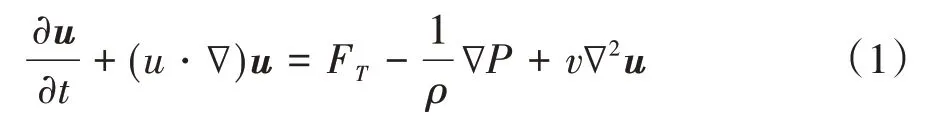
式中：v为动力黏度；ρ为液体密度；P为流体压力；u为流体的速度矢量；∇为拉普拉斯算符.

2）粒子追踪场

采用了欧拉-拉格朗日法对运动颗粒进行追踪，同时采用牛顿第二定律描述运动过程.欧拉-拉格朗日法采用式（2）记录每个粒子的不同状态.

式中：mp为颗粒质量；vp为颗粒速度；F为颗粒受力.

1.3 模型验证

首先采用宏观试验对COMSOL 数值模型进行验证.依据Petrov 等［9］试验结果，建立COMSOL 数值模型，并采用稳态对蠕动流场进行模拟，得到渗透系数分布图如图1 所示.计算得到渗流出口的渗透系数k为1.57×10-11m/s，与试验渗透系数比值为1.121.同时，分别建立其他试验结果的COMSOL 数值模型，得到的渗透系数与试验对比汇总如表1所示.由表1可知，该COMSOL 数值模型能够较好地模拟GCL 在去离子水渗透时的工况.其次采用宏观流场对COMSOL 数值模型进行验证.在本文的仿真模拟过程中，宏观流场（图1 所示）的规律与金磊等［27］的研究结果类似，即在孔隙通道半径大处流速增加明显.同时，本文流场速度随孔隙通道半径增大而增大，其结果与梁越等［28］的研究结论一致.

图1 渗透系数分布图（n=0.4）Fig.1 Distribution of the hydraulic conductive（n=0.4）

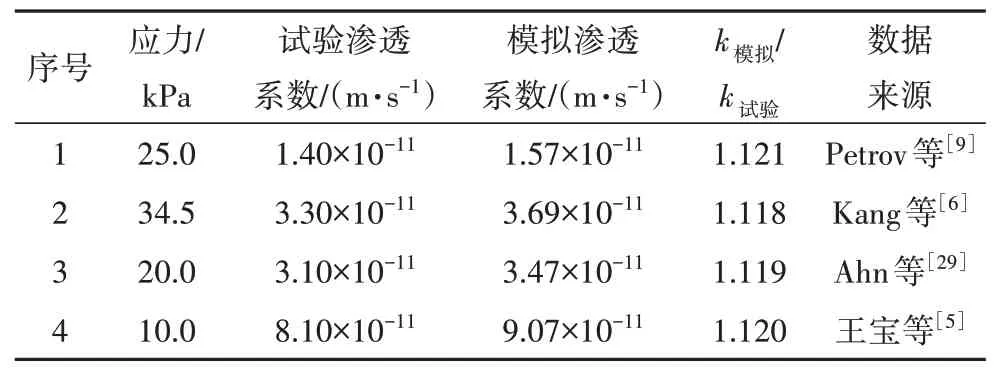
表1 模型准确性对比分析Tab.1 Comparative analysis of the model accuracy

1.4 几何模型建立

1.3 节验证了COMSOL 中的蠕动流场可对GCL的层流运动进行宏观模拟.由于在孔隙率不变时，等效渗透系数与孔隙尺寸的平方成正比［30-31］，考虑到有限元计算的时效性，采用几何相似性理论，将验证模型尺寸进行适当扩大，进行下列计算.同时，也有研究发现颗粒的几何外形［32］对其渗透系数的影响并不显著，因此，本模型构建边长为10 mm 的大正方形表示GCL试样，交错布置9×9边长为1 mm的小正方形表示膨润土颗粒，在孔隙率n=0～1范围内进行优化计算.

已有学者［33-35］研究发现，在膨润土膨胀过程中的晶体膨胀阶段，是膨润土固相颗粒的膨胀间距不断增大的膨胀过程，即颗粒几何尺寸扩大而孔隙率减小的过程.同时采用正方形的放大命令，确保模型膨胀前后几何外形一致，也可保证模型达到所需的最小孔隙率，实现模拟孔隙率n=0～1 的全区域变化过程.因此通过COMSOL 内逐渐放大小正方形的命令模拟颗粒膨胀过程，从而控制几何模型的孔隙率逐渐变小，部分工况如图2 所示.选用蠕动流模块和流动粒子追踪模块进行瞬时计算，通过实时监测流动粒子的位置坐标，最终确定液体在多孔介质内流通的渗流路径.

图2 不同孔隙率下的几何模型Fig.2 The geometric models for different porosities

1.5 边界与初始条件确定

蠕动流模块边界条件设定为小正方形（颗粒）外围及大正方形（膨润土试样）上下边界均为封闭边界，流体受压力P作用下，从左边界流入，右边界单向流出.

流动粒子追踪模块边界条件为粒子均匀排布在左边界，由蠕动流中的速度场控制粒子运动至右侧壁，最后附着在右侧壁上后其速度为0.上下边界、小正方形外围边界均为保持粒子动量守恒的粒子反弹壁，使得粒子在接触到上述边界后立即反弹，速度大小不变，不发生动能损失.整体COMSOL模型边界条件如图3所示.

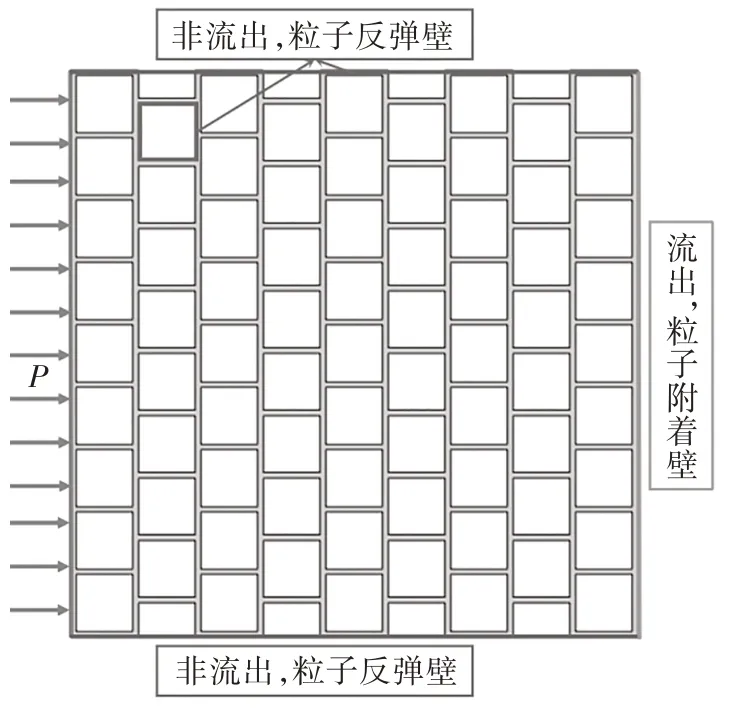
图3 GCL简化几何2D模型Fig.3 The simplified geometric 2D model of the GCL

工程实际中，垃圾填埋场中GCL 衬垫上部渗滤液收集系统及第一层垃圾体上覆荷载一般约为14 kPa［36-37］.因此，模型取入口边界压力为P=14 kPa，该条件同时满足蠕动流场雷诺数小于1 的要求.模型参数详见表2.

表2 模型参数确定Tab.2 Setting parameters of the model

1.6 网格划分

考虑时效性，参考Zimmerman［25］的研究，采用三角形网格进行划分计算，并分别对n=0～1 之间不同孔隙率的多孔介质模型进行模拟.

值得一提的是，在GCL渗透实验中，测得GCL试样的初始孔隙率一般为0.6［5，37］.但当垃圾填埋场开始服役时，GCL 衬垫在吸水膨胀与上覆荷载作用下，孔隙率的数值将明显减小［38-39］.同时，Seiphoori 等［40］对MX-80 膨润土试样进行膨胀试验后表明，不同压实状态下膨润土的孔隙率介于0.34～0.58 之间，因此，以下主要以孔隙率n=0.41 的工况为例进行分析计算，具体网格划分如图4所示.

图4 网格划分Fig.4 Mesh division

2 仿真结果与分析

2.1 蠕动流计算结果

基于COMSOL 软件自身的求解器的特性，一般认为稳态求解可用以验证瞬时求解的结果是否趋于稳定，而瞬时求解有利于分析宏观试验现象随时间的变化趋势，因此，将蠕动流场和粒子追踪模块进行耦合瞬时计算.

首先，采用稳态对蠕动流场进行模拟.入口边界选取充分发展的流动命令以减少边界效应，即当流体到达左边界（入口）时，水流趋于平稳，这样可以有效地减少因为边界加压而导致的入口处水流速度不均匀的现象.图5 所示为模拟试样中流体的速度图与压力矢量图.在速度矢量图（图5（a））中，可观测到A、B、D 点处路径的最大速度小于C 点处最大速度.分析原因是C 点的水流速度源自上、下两侧竖向通道，类似于通道半径在此处增加.因此，根据泊肃叶公式，通道半径增加会导致水流速度增加，即通道个数直接影响流速.同时，由压力矢量图（图5（b））可见，粒间孔隙压力从左到右（出口）出现均匀递减的趋势.此外，图5（b）左边界下部压力分布（虚线）比上部压力分布（实线）更紧密，主要原因是几何模型孔隙通道布置不均匀，导致压力在上、下边界上出现不均匀分布.

2.2 流动粒子追踪

在瞬时状态下，将蠕动流场和粒子追踪模块进行耦合计算.模拟过程中发现粒子追踪场在20 000 μs时基本达到稳定流的速度状态，因此，仅监测流动粒子在t=0～20 000 μs 内的位置坐标.图6 给出了部分时刻流动粒子轨迹图.

对比图5（a）和图6（a）可知，微观流动粒子分布呈现与宏观流体场分布类似的规律.图6（a）中，E、F点路径内的最大速度小于G 点的最大速度（实线所示），分析其原因是G 点等效通道半径增加，导致速度增加；在相同的原因下，导致H 点的最大速度小于I 点最大速度（虚线所示）.因此，图6（a）中宏观蠕动流场是细观粒子流动场作用的结果.

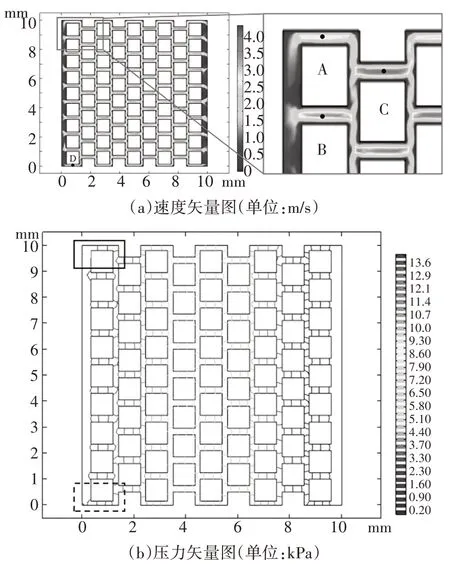
图5 试样中流体速度图与压力矢量图Fig.5 Fluid velocity and pressure vectors in the specimen

但同时对比发现，图6（a）中蠕动流场平均速度为1.53 m/s，因此，如果不考虑曲折度影响，粒子按直线规律运移的话，应该在t=6 535 μs 时到达右边界.然而，如图6（d）所示，实际粒子运移中，当t=6 535 μs时，其仅运移到距右边界一定位置处（图6（d）中虚线所示），而在t=8 000 μs（约为整体运移时间的前三分之一）时，大部分粒子才到达右边界，少数粒子甚至需要比这更长的时间（如图6（e）所示）.这是由于流径具有一定的曲折度，使得粒子实际运移路径大于直线距离.此外，观察图6（b）～（e）（粒子运移过程）可发现，在流体速度控制下，流动粒子先从左边界均匀分布，通过粒间孔隙通道，通道较窄，速度增加，随后发生分流，在上、下侧通道内速度减缓；继续通过粒间孔隙通道，通道收窄，速度再次增加.依次反复后，流动粒子呈不均匀状黏附在出口处.

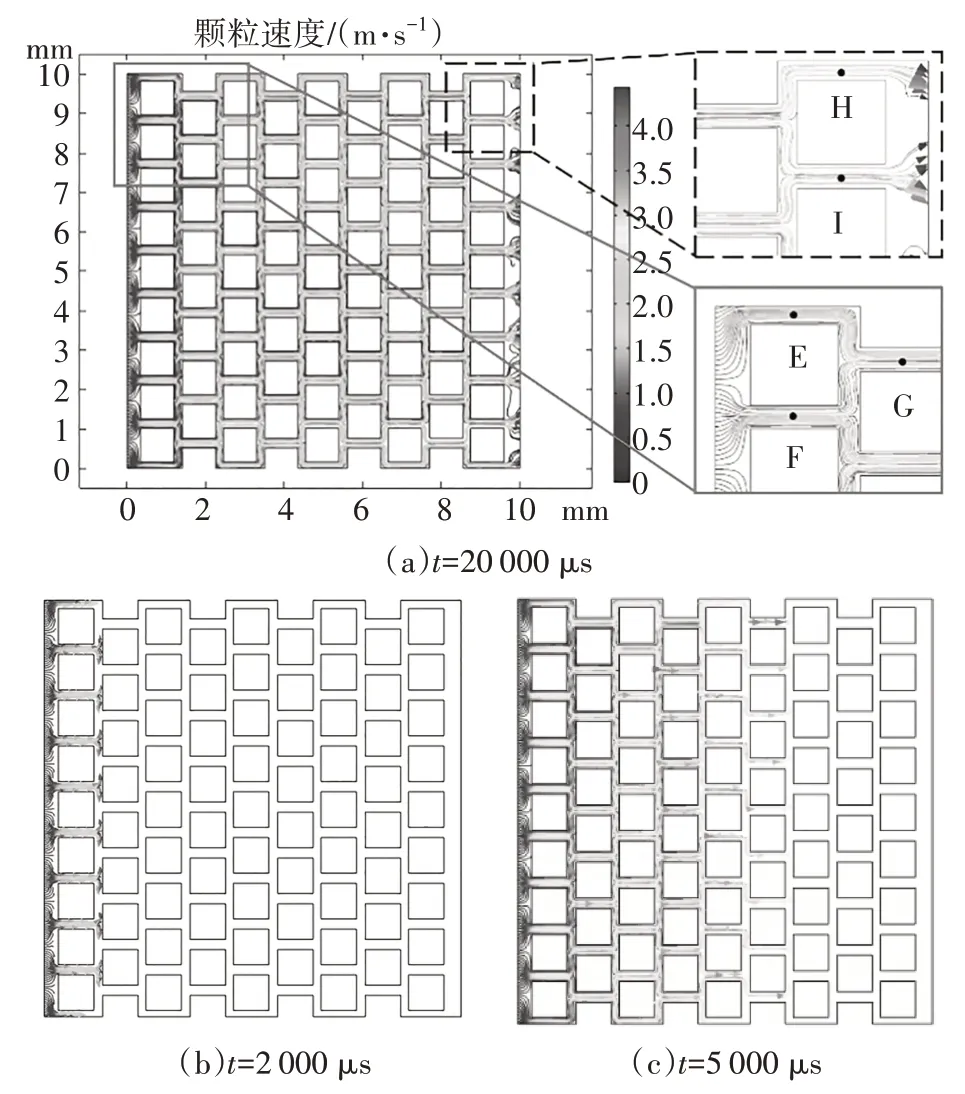
图6 流动粒子轨迹图Fig.6 The trajectory of the particle flowing

2.3 GCL渗透系数理论预测模型

GCL 衬垫中起主要防渗作用的膨润土是一种多孔介质.Kozeny［12］和Carman［13］提出了预测多孔介质渗透率的半经验公式（Kozeny-Carman（K-C）方程），该式适用于多孔介质渗透系数较低的情况.首先，Nooruddin和Hossain［14］在K-C方程基础上，将土体通道简化为毛管模型［41］（图7）.长度为L、截面面积为A的多孔介质土体（图7（a）），此时的固相颗粒为不规则分布，由孔隙组成的渗流通道也不均匀分布，均质土体的固相颗粒一般为土颗粒；采用等流量条件下渗流通道的等效毛管化，将土颗粒规则排布后，形成土颗粒以外的孔隙通道，等效后为直径2R的通道（图7（b））；但由于土体的实际渗流路径如图7（c）中实线所示，即在土颗粒与土颗粒之间形成曲折的路径；假设该路径中孔隙通道直径为2r（r≤R），如图7（d）所示，以此形成等效毛管模型来表示液体在多孔介质中的移动规律.

图7 渗透通道等效毛管化分析示意图Fig.7 Schematic of equivalent capillary of permeation channels

同时，由于土体的渗流路径L具有一定的曲折性.Collins［41］采用曲折度τ来反映多孔介质中平均有效流动路径长度Li（m）与流体流动方向的直线路径L（m）的比值，如公式（3）所示.不少学者［42-47］对曲折度τ进行进一步研究后发现，孔隙率与曲折度的关系可通过数学表达式进行表述，如表3所示.

表3 孔隙率与曲折度关系Tab.3 Relationship between porosity and tortuosity

由于膨润土具有自相似性，因此可将土颗粒通过单位体积法简化为单元体.同时，将简化后的单元体表示为毛管模型，以便通过渗流路径获得渗流的等效理论模型.本文等效模型作如下假设：假设在等效渗透通道模型中，总共有M根半径为ri、长度分别为Li的毛管束.结合修正的哈根-泊肃叶［48-49］方程可知，单位时间内通过M根毛管的渗流速度q（m3/s）为：

式中：μ为渗滤液的动力黏度，Pa·s；ρw为液体的密度，kg/m3；g为重力加速度，m/s2；π=3.141 59；ri为在M根弯曲毛管中，第i根毛管的通道半径，m；Li为第i根毛管的渗流长度，m.

将式（3）代入式（4），得通过土体的总流量Q（m3/s）为：

又由达西定律可知，水流通量J（m/s）与水力梯度ΔH/L成正比：

式中：k为渗透系数，m/s；ΔH为水力梯度；L为渗流路径，m.

由于水流通量J是总流量Q与土体截面面积A（m2）的比值（J=Q/A），将式（6）代入式（5），换算可得渗透系数k为：

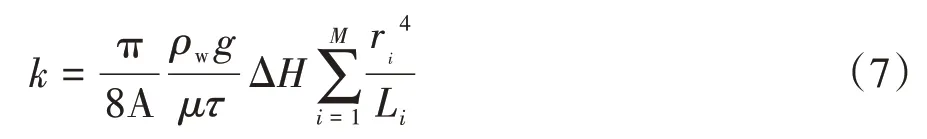
值得一提的是，尽管式（7）中的曲折度τ是基于多孔介质本身性质的参数，其难于用试验手段直接测得，但可以通过孔隙率n计算获得（见表3）.

因此，本文孔隙率n从0 到1 的一系列COMSOL模型，采用流动粒子追踪方法获得孔隙率全范围内流动粒子的运动轨迹，并统计计算相应的渗流路径以及曲折度，模型选取的试验验证参数如表4 所示.由此计算得到不同孔隙率与曲折度之间的关系（图8中散点标示），可以看出，曲折度随着孔隙率的增加而减小.

表4 试验验证参数［50］Tab.4 The experimental parameters verification

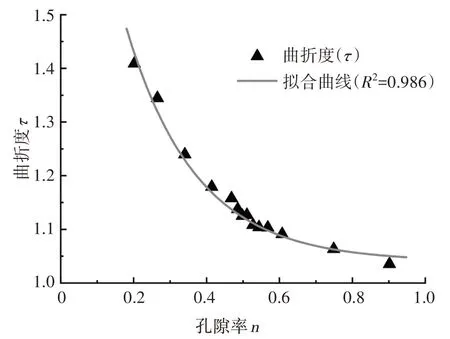
图8 孔隙率与曲折度拟合图Fig.8 The fitting curve of porosity and tortuosity

由拟合模拟的一系列工况所得结果（图8 中实线标示），可得到孔隙率与曲折度之间的数学表达式为：

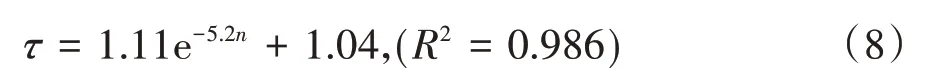
将式（8）代入式（7）中，即可得到能综合反映孔隙率与流径曲折度影响的GCL 渗透系数理论预测模型：

为验证式（9）的准确性，本文采用大量已有试验结果（Chai 等［50］、Jo 等［51-52］、Petrov 和Rowe［53］、Chen等［54］、Setz等［55］、Bradshaw和Benson［56］以及Seiphoor［57］）进行计算比较，结果如图9 所示.以Chai 等［50］数据为例，具体的计算过程如下.

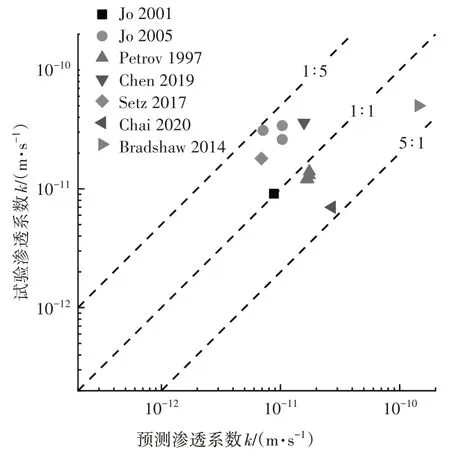
图9 GCL预测渗透系数与试验渗透系数Fig.9 Predicted and measured hydraulic conductivities of the GCL

由式（9）可得此时GCL的预测渗透系数k：

此时，所得预测结果和试验结果比值为：

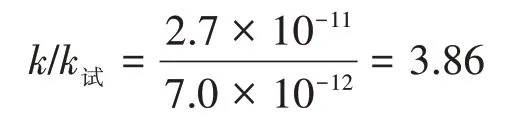
本文采用对数坐标系下渗透系数偏差分析的表示方法［58-61］（如图9 所示）.图中，横坐标为预测渗透系数值，纵坐标为试验渗透系数值.从图中可看出，预测值与试验值的范围为0.23～3.86.按照行业标准《钠基膨润土复合防水衬垫》（FZ/T 64036—2103），渗透系数值的误差常在一个数量级内进行表征，如规定渗透系数≤5×10-9～1×10-10cm/s.同时，对数坐标系下渗透系数的偏差一般介于1/10～10［37，58-61］.本文GCL 的理论预测模型计算结果与试验值的比在1/5～5，小于一个数量级，说明该GCL 理论预测模型可以较为准确地用于预测GCL 的渗透系数，可以指导工程实际.

3 结论与展望

本文通过COMSOL 模拟了GCL在膨胀变形过程中，曲折度随孔隙率的变化而变化的规律，得到多孔介质渗流流径的细观模型，研究了孔隙率和流径曲折度对GCL渗透系数的影响，主要结论如下：

1）当入口边界条件为均匀压力时，在蠕动流场中，流体通道半径的增加会导致流体速度增加，同时，流体压力从入口到出口处呈现均匀递减的趋势.

2）GCL 试样中，微观流动粒子分布与宏观流体场分布规律基本一致，且大部分流动粒子在整体时间的前1/3段完成运移.

3）GCL 试样中，流径的曲折度随孔隙率的增加而减小，且呈指数函数关系.

4）提出的能综合反映孔隙率与流径曲折度影响的GCL 渗透系数理论预测模型，可以较为准确地预测试验结果，两者比值介于1/5～5.

需要注意的是，本文膨润土曲折度与孔隙率之间的关系主要是基于模拟均一几何尺寸和均一几何孔隙表征膨润土试样得到的.因此，研究结果可以从概念上定性地分析曲折度随膨润土颗粒膨胀的变化规律，同时反映曲折度对GCL 渗透系数的影响.但是，后续还需要对大量不规则试样展开进一步的深入和系统的研究，才有可能将研究结果推广到定量分析以及实际应用中.