标准容器移动窗口式存储异类无序对象
2022-10-09刘健
刘 健
(1.四川开放大学高职学院,四川 成都 610107;2.四川华新现代职业学院信息中心,四川 成都 610107)
0 引言
现已有多种存储数据的常规算法,相关算法也在实践应用中得到了证明和推广。该文讨论的算法涉及2个队列:对象队列和容器队列,显然不能简单套用已有的普适性算法,必须在该基础上进行改进。
现实生活中的实际需求不会一成不变,更不可能恰好匹配常规算法的要求。实际情况常需要综合运用2个或多个常规算法,还要掺杂一些特殊要求。在现实的生产生活中,工作人员还可以借助通用型的工业软件,通过半手工操作的方法来进行常规算法形式的运算,这种方法的效率极低。当遇到某些特殊需求时,这种半手工的方法就完全无法满足要求。该文采用移动窗口的方式来消除若干个对象间的社会联系,这是半手工方法根本不能胜任的任务。
1 背景介绍
该文讨论的问题来源于一个经常出现的现象:人或物在一个特定的环境里按照一定的规则安排存放的位置或场地。这些人或物可以抽象为对象,若干个人或物就组成对象队列。当然,这些人或物之间是要分类的,分类后就构成异类的对象队列。当这些对象刚出现时,都是无序的。至于这些对象要存放的位置或场地就可以抽象为容器。因为人或物可能会经常更换,所以不能对这些对象有过多要求。而容器相对来说不会频繁更换,可以按照特定的标准统一生产或配置。
2 前置条件
2.1 标准容器
所有容器都是标准化的容器,记为container(=1,2,…,),其容量记为capacity(=1,2,…,)。每个容器内部都划分为若干个小格,称为存储格,记为cell(=1,2,…,;=1,2,…,capacity)。容器中存储格的数量就是这个容器的容量。
每个容器内部的存储格之间没有区别,即尺寸、容量、和功能都一样,而相同类型的容器与容器间在功能上也没有区别,都可以存储同类对象,这就是标准容器。标准容器利于存储个体间有细小差异的同类对象。
2.2 对象和容器分类
对象有其自身的类型,根据对象类型的不同,对存储格的要求也不同,于是就需要对存储格进行分类。因为每个容器内的存储格性质都相同,所以存储格的类型就决定容器的类型。存储格的类型与容器的类型一致,并与存储对象的类型一致,如公式(1)所示。
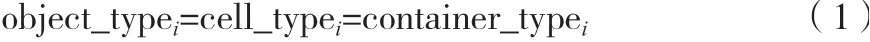
式中:object_type(=1,2,…,)为对象的类型;cell_type(=1,2,…,)为存储格类型;container_type(=1,2,…,)为容器的类型。
既然3个实体的类型都必须一致,那可以把3个类型都简化为1个类型,如公式(2)所示。
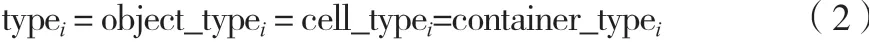
式中:type(=1,2,…,)为3个类型统一。
当对象异类时,就需要异类容器去匹配相应类型的对象,以满足相应的存储要求。对象类型的数量决定容器类型的数量,这就解决了标准容器存储异类对象的问题。
2.3 容器的容量
因为是标准容器,内部的存储格必须一致,所以可以将相同类型容器的内部存储格数量设定为相同,即同类容器的容量都一样,这样便于对容器进行生产和管理。这种情况是一种理想状态,实践的过程中很难满足这种极端条件,如公式(3)所示。

式中:capacity为容器的容量,=1,2,…,。
由于容量都一致,因此可以简单记为。
在实际运用中,因为现场地理条件等各种因素的影响,不一定只允许相同容量的容器存在,所以需要为每个容器设定自身的容量,此时各个capacity的值不尽相同。但每个容器的容量都不能超过标准容器的容量,即满足公式(4)。

式中:为标准容器的容量;capacity为各个容器的容量,=1,2,…,。
2.4 容器的优先级
虽然同类容器的功能一样,但是实际每个容器的内部构成并不一定完全一致,只要满足容器分类的标准即可。在使用的过程中,就需要对容器的使用顺序进行排序。对每个容器指定一个优先级,记为rank(=1,2,…,),优先级别最高的最先使用,以rank为最高优先级。当然也可以优先级别最低的最先使用,这只需要倒序排序即可。在实际操作中,正序和倒序对结果没有影响,简单说就是排在最前的容器最先使用。
因为存在非标准容器,所以为保证标准容器优先使用,就需要保证大容量容器的优先级高于小容量容器,即满足公式(5)。

式中:capacity(=1,2,…,)为排序后各个容器的容量。
2.5 异类无序对象的存在状态
对象以批量的形式存在,即对象是整体出现或整体消亡的无序队列,不是单个出现、逐个到达后形成队列的。整个无序队列存储进标准容器后,再经过后续的相关阶段,容器整体清空,待下个无序队列存储及使用。对象有批次的区分,各个批次之间有时间顺序,不能同时存在。
对象队列里存在各种类型的节点,因为是无序队列,所以队列里相邻节点的类型不一定相同。当相邻节点类型一致时,有可能出现若干个相邻节点间的非技术性社会联系。为消除这些社会联系,就采用移动窗口式的手段使这些节点交错分离,分别存储在当前窗口内的若干个容器里,而不是连续存储在同一个容器里。
3 存储步骤
3.1 锁定容器
在开始存储对象前,必须锁定现场所有容器,因为此时尚不知道当前对象的类型,所以是锁定所有容器。锁定后,不允许其他指令与该指令并行运行,即使是读取存储容器状态也不行(后续的操作都具有严格的排他性)。
如果有2个指令集并行运行,就会出现脏数据,后续的操作结果都是脏数据。存储对象的操作只能是串行运行的,即当某个操作指令集到达时,发现全部容器已经被排他性锁定,只能等待前一个指令集操作完毕、释放容器后,才能对容器进行锁定操作。
3.2 判断位置
在存储列表中搜寻当前指令的对象是否已经存在存储位置cell。如果有,就直接跳过后面的存储流程,此时≠null并且≠null(1,1≤y≤capacity,null表示空)。如果没有,就进入下面的存储流程,当=null并且=null时,进入步骤3.3。
3.3 选择对象匹配的容器类型
根据对象的类型选择适合的容器类型,即根据type选择类型一致的容器,抛弃不符合需求的容器。后续的操作都不再涉及容器类型的问题,因为此处已经作过类型筛选,只保留满足需求的容器,所以默认的操作都是在同种类型的容器上完成的。
3.4 存储对象
首先,设定1个窗口值,采用伪随机的方式把连续的个对象平均分配到个容器里去,目的是切断这些对象间的社会联系。伪随机的方式有很多种,为计算简单、运行高效,目前采用的是取模方式,即根据对象的下标取模,把个对象分别依次存储到个容器里,下一轮的个对象也一样,后面的对象存储方式以此类推,直到窗口所在位置的个容器全部填满。此时,窗口向后移动,跃过当前的个容器,去覆盖后面的个空闲容器。上一个窗口所在位置的个容器已经填满,就处于关闭状态。此时,窗口所在位置的容器还没有存入对象,处于就绪状态,等待下一个对象的到来。
这样,看上去就像窗口在不停地移动,因此称为移动窗口式存储。理论上来说,的取值范围为1 ~。当= 1时,全部容器根据优先级依次使用,不存在伪随机的存储方式,也就不能发挥消除对象间社会联系的作用。当=时,把全部的容器同时放在最大的一个窗口里,全部的容器同时处于就绪状态,整个对象队列会平均分配到全部的容器里。显然,在实际操作中的取值不应该是两头的极限,即≠1并且≠。
此时,判断存储列表是否为空。如果为空,就进入步骤3.4.1;如果不为空,就进入步骤3.4.2。
当存储列表为空时,就表明还没有任何一个对象已经存储到此类容器中,此类容器全部都是空闲状态。因为容器已经事先根据优先级排序,所以根据这类容器的优先级别最高级rank把当前对象直接放在存储列表的首位,即第1个容器container的第1个存储格cell。因为是存储列表的第1条信息,所以要单独处理。
获取存储列表中存储格cell的最大值,即和的最大值。因为存储顺序是根据容器的优先级rank和容器内存储格cell的排列次序执行的,所以cell就是存储列表末尾的那个值。
对进行的取模运算,即可获得当前窗口的位置。当前窗口的第1个容器为container,如公式(6)所示。
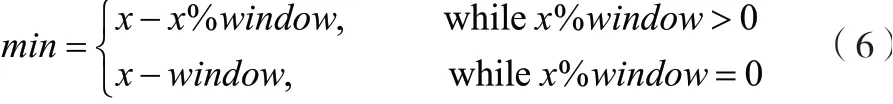
式中:为当前窗口第1个容器的编号;为窗口的尺寸;为存储列表末尾容器的编号。

当前窗口的最后1个容器为container,如公式(7)所示。式中:为当前窗口的最后1个容器的编号;为窗口的尺寸;为当前窗口第1个容器的编号。
不能简单计为(+-1),当窗口移动到最后1个位置时,窗口内的容器数量有可能小于窗口的值,而且出现这种情况的概率非常高。在实际操作中,容器队列的数量基本是固定的,而窗口是可变值。让容器数量刚好为每个窗口的整数倍,这几乎是不可能的事。
在确定和的值后,就可以确定当前窗口所在的位置。而container就是当前窗口里的当前容器,cell就是当前容器里的当前存储格,当前对象就应该存储在当前存储格cell的“下一个位置”。这个“下一个位置”有可能是下一个容器的相同位置的存储格cell,也有可能是当前窗口内第一个容器的下一个存储格cell。
此时,对当前窗口内的所有容器进行遍历查找,目的是寻找合适的存储位置。以当前容器container为起始位置,获得下一个容器container。如果container还有空余存储格,即当capacity>时,那么当前对象就存储在容器container的存储格cell里。如果container已经填满,即当capacity=时,就获取再下一个容器container。以此类推,直到查找到当前窗口里的最后一个容器container为止。
在完成此轮遍历查找后,如果没有寻找到合适的存储位置,就表明当前窗口内当前容器后面的容器都已经填满,能据此判断这样结果的原因就在于前置条件2.4的容量优先级。既然这些容器已满,那只能回到当前窗口的第1个容器container查询空余位置。
如果container还有空余位置,即当capacity>时,当前对象就存储在容器container的存储格cell 里。如果container也已经填满,就表明当前窗口已满,即整个窗口内的全部容器都已经填满,只能移动到下一个窗口。当前对象就存储在容器container的存储格cell里,可以判断当前窗口已满的原因也是前置条件2.4的容量优先级。
3.5 收敛窗口
当存储操作达到阈值时,就要对窗口值进行收敛。这个阈值就是当窗口移动到最后一个位置,即在最后一个窗口内操作时,即为达到阈值。可以用对象剩余量与当前窗口的容量比较值作为标准,以判断是否已经到达最后一个窗口,如公式(8)所示。

式中:为对象队列的数量;capacity为第个容器的容量。
这时,就已经到达最后一个窗口。
由公式(8)可以推导出公式(9)、公式(10)。
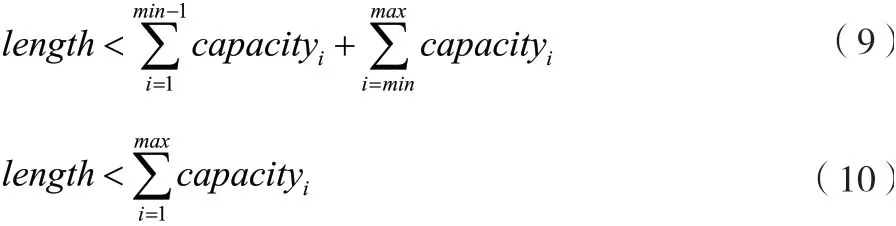
由公式(10)可知,判断标准更简洁,从代码的实现程度来说,难度也降低了。并且公式(10)的实际意义可以解释为对象的数量小于窗口所覆盖过的全部容器的存储量的总和,包括最后一个窗口。窗口所覆盖的全部容器不一定是整个容器队列,其数量有可能比整个容器队列的数量少。
此时,不再使用窗口的预设值,而是把窗口收缩到最小值,即设置= 1。收敛窗口的目的是在最后一个窗口内不作伪随机的平铺式存储,而是根据容器的优先级依次存储。
如果继续采用伪随机的平铺式存储,那么必然会浪费最后一个窗口内容器的存储空间(最后一个窗口内的全部容器都会处于半空状态,即每个容器都存储部分对象,同时还有空余存储格)。
因为开启容器就意味使用链条上的资源都必然配合开启,所以半空状态的容器必然也会浪费链条上、下游的资源。
在设置= 1后,则继续步骤3.4.2,直至对象存储完毕。整个流程如图1所示。

图1 存储流程
4 应用实例
该文承载项目的单位每年举行参与人数众多的招录考试,高峰时人数达到3 413人。该实例就以该数量为试验数据进行演算。总体数据都处于无序状态,形成1个没有排序标准的无序队列。每个个体都可以抽象为1个对象,全部的对象就形成无序对象队列。其中,有效数据3 300个,无效数据113个。有效数据分2类,第Ⅰ类为3 179个,第Ⅱ类为121个。为对象安排位置就可以抽象为存储进容器里的存储格,该试验容器准备情况为第Ⅰ类标准容器105个,容量都为30;第Ⅰ类非标准容器3个,容量分别为20、15和15;第Ⅱ类标准容器6个,容量都为30。
该实例采用SQL语言实现算法,形成存储过程,再使用查询语句逐个对象调用存储过程,模拟工作人员逐个安排存储位置。试验环境为Interl Xeon CPU E5-2609 v2 @ 2.5GHz,Windows 2003,SQL Server 2005 SP4。总共进行10次试验,每次的取值都为1~10,试验耗时结果见表1。

表1 试验耗时结果(单位:s)
上述结果表明,窗口值的浮动对运行时间的影响极小,每次运行的时间差异非常小,耗时差最大值也仅为58-48 = 10 s。这跟运行环境紧密相关,试验的服务器同时运行多个虚拟机,因此其他虚拟机的服务对CPU、内存和硬盘的使用都会影响试验结果。图2可以更直观地表述相关结果。
图2 试验耗时结果
通过上文可以得出结论:对窗口大小的设置不影响实用方案的选择。根据多年的经验积累,最终实际选择
= 3。
无效数据基本都是信息不全造成的,在补齐信息后即可转换为有效数据。因为前面3 300个有效数据已经安排完毕,所以此时不再由SQL查询语句调用存储过程,而是业务层通过业务逻辑层传递参数调用存储过程,完成单个数据的存储位置安排任务。
5 结语
该文所阐述的算法来源于普通的招考录取社会现象,根据多年的实践最终抽象为“标准容器存储对象”的问题。
在解决该问题前,都采用传统的人工方式分配位置。当对象数量大约为2 000个时,工作人员需要3个工作日才能完成任务,而且必须是全程只处理这一件事,不能同时处理其他事务。当对象数量大于3 000个时,通常工作人员需要4~5个工作日才能完成。在实际运行中,该流程所许用的时间常少于4个工作,工作人员必须在非工作时间继续处理这个问题。
在提出该算法后,真正的处理时间小于1 min,提升了工作效率。即使是性能并不出众的服务器仍然可以在非常短的时间内达到预期结果。
