一种基于合作博弈的深度调峰补偿策略

范峻伟，朱继忠*，史普鑫，郭万舒，史沛然，江长明

（1．华南理工大学电力学院，广东省 广州市 510641；2．国网华北分部电力调控分中心，北京市 西城区 100053）

0 引言

近年来，受国家政策与市场因素的推动，可再生能源发展迅猛，新能源装机实现了跨越式增长[1]。国家主席习近平提出中国将于2030年前实现“碳达峰”，2060年前实现“碳中和”的目标，新能源发电占比将持续提升。现阶段，风电的大规模并网严重削弱了电力系统调峰能力[2-3]。此外，随着风电装机规模不断增长，其渗透率也逐年提高。同时，风力发电的不确定性、反调峰特性及难预测等特点[4-5]使得系统峰谷差和调峰难度大幅增加，传统火电与风电等新能源间的协调发展出现矛盾[6]。为尽可能地消纳新能源，社会各方不断呼吁火电机组增加调峰深度[7]。在现行的调峰考核及补偿机制下，调峰成本完全由火电机组承担，但现有的深度调峰费用补偿计算方法较为粗糙，且补偿机制难以保证火电机组的基本收益，火电机组参与深度调峰的积极性无法被充分调动。因此，如何在现有的调峰补偿机制基础上进行改进与完善，鼓励火电机组积极参与深度调峰，已成为保证当前电网安全稳定运行亟需解决的问题。

在火电机组参与深度调峰的经济性方面，文献[8-9]建立了火电机组处于不同深度调峰阶段的成本模型，优化目标为系统总运行成本最小，得到了经济性最优的电力系统深度调峰调度方案；但文章没有深入分析火电厂和风电场在调峰交易中单位机组的具体收益。

火电机组参与深度调峰积极性低的重要原因是没有合理安排风电并网后的利益分配，已有较多文献提出调峰后的利益分配方法。文献[10]提出了将部分弃风收入补偿给调峰机组的矛盾协调机制，确保火电机组参与调峰市场的利润高于不参与调峰市场的利润。文献[11]基于卡尔多改进方法，提出了一种新的风火复合系统深度调峰机制，并探讨了如何通过调整参与者利益分配以挖掘系统的深度调峰潜力。文献[12]基于火电机组容量差异，对不同类别机组采取不同的有偿调峰与无偿调峰的划分界限，提出了考虑机组调峰能力实现程度的补偿模型。

调峰费用的补偿及分摊本质上属于机组之间的博弈问题。文献[13]基于Shapley值法和调峰里程法进行机组调峰的费用补偿。文献[14]分别建立燃煤发电机组调停调峰成本的无嫉妒性分摊模型、虚拟价格分摊模型和Shapley值分摊模型，并进行了分析比较。文献[15]通过核心法和Shapley值法对深度调峰收益进行分配。以上方法均存在机组数量增多时计算出现“维数灾”的问题，且未量化机组参与深度调峰的意愿程度。

对此，本文在已有研究成果的基础上，对火电机组的调峰能力及深度调峰后的机组补偿策略进行研究。首先分析火电机组的调峰过程，建立了机组不同调峰阶段的成本函数。其次，考虑机组调峰主动性及调峰补偿的倾向度，结合优劣解距离法，构建以相对满意度最大为目标的调峰补偿策略模型；分析了当前中国调峰市场中火电机组参与深度调峰时的阶梯式报价模式。最后，建立以火电机组总发电成本最小为目标的电力系统经济调度模型。算例分析了火电机组参与深度调峰的经济性，并验证了本文所提补偿策略的有效性。

1 火电机组深度调峰

1.1 火电机组深度调峰过程

火电机组调峰能力是指机组出力跟踪系统负荷变化的能力[16]。根据机组运行时的燃烧介质和燃烧状态，一般情况下，调峰过程可以分为常规调峰（routine peak regulation, RPR）、不投油深度调峰（deep peak regulation without oil, DPR）和投油深度调峰（deep peak regulation with oil, DPRO）[17]三个阶段，如图1所示。其中Pmax和Pmin分别表示火电机组在常规调峰阶段的最大出力和最小出力，Pa和Pb分别表示火电机组在不投油深度调峰和投油深度调峰阶段的最小出力。

当火电机组出力介于Pmax和Pmin之间时，机组运行在常规调峰阶段。当风电出力较大时，需扩大火电机组出力范围以消纳更多的风电，要求机组降出力至Pmin和Pa之间，此时机组处于不投油深度调峰阶段。当机组处于投油深度调峰阶段时，功率需进一步下调，并对机组进行投油助燃，此时要求火电机组出力介于Pa和Pb之间。

1.2 火电机组深度调峰成本

1）煤耗成本。

在传统调度模型中，火电机组在常规调峰阶段的煤耗成本近似为二次函数。深度调峰时，若对精度要求不高，机组煤耗成本可近似为常规调峰阶段的煤耗成本，具体表示如下：

式中：ai、bi、ci分别为经济折算后火电机组i的调峰煤耗成本系数；Pi,t表示火电机组i在t时刻的出力。

2）损耗成本。

火电机组进入深度调峰阶段后，在交变应力和高温的持续影响下，发电机转子金属会产生低周疲劳损耗和蠕变损耗，使机组的寿命降低[18]，影响机组运行的安全性与经济性。参考Manson-Coffin公式粗略计算深度调峰阶段的机组损耗成本[19]，表示为

式中：λ为火电机组实际运行损耗系数，且满足λDPR＜ λDPRO；Ci,unit为火电机组购机成本；Nf( Pi,t)为转子致裂循环周次。

3）投油成本。

机组进入投油深度调峰后，要求出力进一步降低。为维持锅炉和水循环系统稳定工作在最低水平，需要对机组进行投油助燃以保证其安全运行，成本表示为

式中：Qi,oil为火电机组i处于DPRO阶段时的油耗量；Soil为当季油价。

综上，火电机组不同运行状态下的出力不同，其调峰成本构成也不同，可表示为如下分段函数：

机组进入DPR阶段后，调峰成本会随调峰深度的增加而上升；进入DPRO阶段后，由于油耗成本的增加，机组成本会陡然上升，曲线大致如图2所示。

2 合作博弈及调峰补偿模型

2.1 调峰主动性

随着火电机组调峰深度的增加，其成本也不断增加，此时机组缺乏主动参与调峰的积极性。火电机组只有在参与深度调峰的收益不低于常规调峰的收益时，才有参与深度调峰的意愿。火电厂调峰主动性表示为

同理，风电场只有在深度调峰交易比常规调峰获益更大时才会选择主动加入。风电场调峰主动性表示为

式中：Rw,before和Rw,after分别表示风电场参与深度调峰前后的收益。

2.2 补偿策略的倾向度

DP（disruption propensity）指标[7]用于定量分析费用补偿对参与者的吸引力，即参与合作博弈的火电机组对该费用补偿策略的倾向程度。其数学意义为参与者i拒绝合作后，给其他参与者带来的损失与自身损失的比值，具体表示为

式中：wi为火电机组i参与深度调峰后的收益；vi为火电机组i拒绝参与深度调峰时的收益；表示火电机组i深度调峰后，其他机组获得的总收益；vn/i表示火电机组i拒绝参与深度调峰时，其他机组获得的总收益；n为参与深度调峰的所有机组总数。

MDP（modified disruption propensity）指标是对DP指标的修正，表示火电机组i拒绝参与深度调峰时，其他机组的平均损失与机组i自身损失的比值。

Di指标值能够反映机组对参与深度调峰所获补偿收益的倾向程度，如表1所示。

表1 MDP指标合作倾向分析Table 1 Analysis on cooperation tendency of MDP index

2.3 补偿策略的相对满意度

优劣解距离法（technique for order preference by similarity to ideal solution, TOPSIS）作为一种多目标决策方法，常用于多方案间的优选。用TOPSIS法能够计算所有机组对不同收益分配策略的相对满意度，从而求解出满意度最高的收益分配策略。

1）收益分配策略系数矩阵。

式中：m为收益分配策略的种类数。

2）理想与负理想分配系数。

3）欧氏距离。

4）相对满意度。

式中：0≤Mj≤1，Mj越接近1表明该补偿策略越接近理想补偿策略，所有机组的相对满意度越高；反之，表明该补偿策略越接近负理想补偿策略，所有机组的相对满意度越低。

2.4 最大相对满意度补偿策略

本文在TOPSIS法和MDP指标的基础上，以调峰收益补偿为背景，提出以最大相对满意度为目标的补偿策略模型。

式中：wi表示机组补偿后的收益；W为所有机组总收益；和分别表示机组i所能接受的补偿后的最小及最大收益。

本文提出的最大相对满意度补偿策略的具体计算步骤如下。

1）根据MDP指标的定义，当Di=1时，可计算得到全体机组所能接受的最小收益（此时的补偿策略称为负理想补偿策略），以及全体机组最小总收益

2）定义系统盈余值ε，表示在所有机组形成的大联盟下，系统能自由分配的收益。由机组实际总收益W和最小总收益Wmin可得，ε=W-Wmin。

4）最后，由上述目标函数及约束条件求解非线性规划模型，便能得到所有机组在相对满意度最大时的收益，即为系统的最大相对满意度调峰补偿策略。

2.5 调峰市场深度调峰补偿

在中国现有的调峰市场中，调峰辅助服务分为无偿调峰和有偿调峰。无偿调峰指规定机组负荷率大于等于深度调峰基准时的调峰辅助服务，属于机组承担的基本义务。有偿调峰指机组主动削减出力至负荷率低于深度调峰基准值。

有偿调峰需对机组进行一定程度的补偿以激励火电机组主动参与深度调峰服务。当前中国深度调峰交易主要采用“阶梯式”的报价方式和价格机制。随机组调峰深度的增加递增报价，并设置报价区间的价格上限，如表2所示。

表2 深度调峰阶梯式报价Table 2 Stepped quotation of deep peak regulation

根据中国现有深度调峰市场的运营规则，火电机组的深度调峰服务费用和系统总深度调峰服务费用可分别用式（18）和（19）表示。

式中：wi为参与深度调峰的火电机组i的服务费；为机组i在第k档于t时段内减少的出力；为机组i在第k档于t时段申报的价格；k=1,2；W为系统总深度调峰服务费用。

深度调峰服务费由交易时段内未参与深度调峰的火电机组和风电机组按各自的上网电量比例进行分摊。

3 基于深度调峰的电力系统经济调度模型

随着风电的大规模并网，为消纳更多的风电，亟需提高火电机组的调峰深度。火电机组深度调峰成本构成复杂，除煤耗成本外还需考虑机组运行的损耗成本及油耗成本。基于以上因素，本文建立了分级深度调峰优化调度模型，以保证电力系统运行的经济性。

3.1 目标函数

在满足负荷及电力系统安全稳定运行的前提下，所有火电机组均参与常规调峰，部分机组参与深度调峰（不考虑机组启停），以调度时段内火电机组总发电成本最小为目标，构建电力系统经济调度模型。

式中：Ctotal为系统总运行成本；T为机组调度时间；N为参与调峰的火电机组个数；Pi,t为机组i在t时段的出力；C(Pi,t)为火电机组不同调峰阶段的成本。

3.2 约束条件

1）功率平衡约束。

式中：Pload,t为t时段总负荷需求值；Pw,t为t时段风电实际上网功率。

2）火电机组功率约束。

RPR阶段：

DPR阶段：

DPRO阶段：

3）风电功率约束。

式中：Pw,t和分别表示风电出力的实际值和预测值。

4）爬坡约束。

式中：Ri,down、Ri,up分别为火电机组的最大向下、向上爬坡功率。

5）备用容量约束。

式中：PJ为系统旋转备用，采用最大负荷的5%。

6）网络安全约束。

式中：Pk,max为线路k最大传输功率。

3.3 模型求解方法

本文中火电机组的调峰成本函数为不连续的分段非线性函数，因而在求解过程中首先需要对成本函数进行分段线性化处理；其次，引入三个0-1变量、分别表示火电机组处于常规调峰、不投油深度调峰和投油深度调峰的状态，如式（32）所示；最后将分段非线性规划问题转化为混合整数线性规划问题[20-21]，再应用商业软件GAMS中的混合整数线性规划（mixed integer linear programming, MILP）对模型进行求解，总流程如图3所示。

4 算例分析

以某地区电力系统为例，假设有5台火电机组，包括2台大容量机组、2台中等容量机组、1台小容量机组，火电机组详细参数见文献[22]。选取机组额定出力的55%、45%及35%分别作为其RPR、DPR及DPRO的出力下限[17]，各机组调峰能力如图4所示。机组实际运行损耗系数在DPR和DPRO阶段分别取1.2和1.5；大容量机组、中等容量机组、小容量机组造价成本分别为3646元/kW、4394元/kW、4863元/kW，其油耗量分别为4.8 t/h、2.8 t/h、1.8 t/h，油价为6130元/t[23]。火电和风电的上网电价分别取0.3元/kWh和0.5元/kWh。

某地区风电场装机容量为1000 MW，选取该地区内春季某典型日的负荷需求及风电出力预测数据，如图5所示。

4.1 不同调峰阶段火电机组成本及收益

为研究火电机组在不同调峰阶段时风电的消纳情况及系统运行的成本和收益变化，分三个场景对模型进行求解。

情景1：所有火电机组只进行常规调峰；

情景2：所有火电机组进行常规调峰和不投油深度调峰；

情景3：所有火电机组进行常规调峰、不投油深度调峰和投油深度调峰。

三种场景下系统的弃风率、成本、收益及净利润对比如图6所示，不同火电机组的具体成本及收益如图7所示。

对比三个场景可知：

1）随着调峰深度的增加，系统风能利用率逐渐提高，从60.24%上升到87.37%，多消纳风电约4328 MWh，风电场总收益增加约216.4万元。

2）机组在DPR阶段消纳大量风电使风电场收益提高，且此时火电机组成本变化不大，系统净利润提高约60万元。

3）尽管投油深度调峰后消纳了更多的风电，但由于火电机组额外增加了耗油成本，使得系统运行成本陡然提高，导致系统净利润反而比常规调峰阶段时的净利润减少约79万元。

4）由于供需平衡，火电机组1出力变化不大，在不同调峰阶段时的净利润变化不大，但其他机组的净利润随着调峰深度的增加明显减少。

4.2 深度调峰补偿

1）市场报价补偿。

本文中，深度调峰市场报价补偿采取阶梯式报价，按机组容量将下调比率分为两档，价格上下限参考中国大部分省份调峰市场设定的申报价格，如表3所示。

由于本文机组较少，为方便与本文提出的方法做对比，在算例分析中直接采用机组每档能申报价格的价格上限进行补偿，不再进行市场竞价。补偿结果如图8和图9所示。

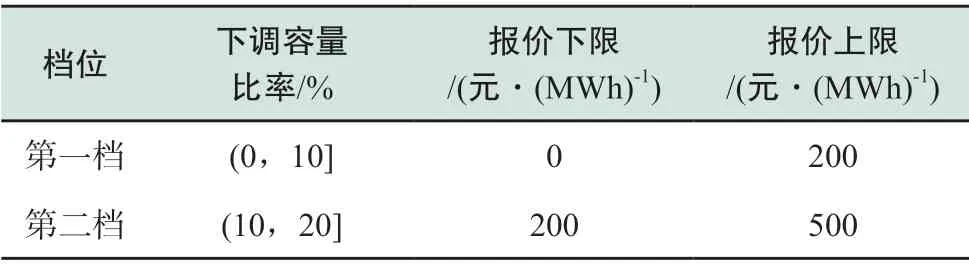
表3 机组深调报价Table 3 Quotation of deep peak regulation

2）最大相对满意度补偿。

应用本文提出的补偿模型对参与深度调峰的火电机组进行补偿，补偿结果如图10和图11所示。

火电机组进行不投油深度调峰后，由于出力减少及损耗成本增加，净利润比常规调峰阶段低，此时火电机组偏向于拒绝参加深度调峰。但由于消纳了更多的风电，系统净利润有所增加。在所提调峰补偿模型中，对火电机组进行深度调峰交易补偿，风电场利润有所降低，但使得所有机组利润均高于常规调峰阶段的值，此时火电机组会有参加不投油深度调峰的意愿。在市场报价模式补偿后，所有火电机组的利润仍低于常规调峰阶段的利润，因此，火电机组在市场报价模式下仍倾向于拒绝参与深度调峰。

火电机组在投油深度调峰后，由于油耗成本的提高，导致其净利润大幅减少，不满足调峰主动性约束，火电机组选择拒绝深度调峰，且此时系统净利润也低于常规调峰阶段的值。因此，除对火电机组进行深度调峰交易补偿，还需对参与调峰的机组额外补偿。在市场报价模式中，经过调峰补偿后火电机组的利润仍低于常规调峰阶段的值，且相比于DPR阶段，DPRO阶段利润减少更多，此时火电机组更拒绝参与深度调峰。在所提补偿策略下，以机组Di指标等于1时求得火电机组与风电场愿意参与投油深度调峰时的最小收益。此时需对火电机组额外补偿约64.6万元，对风电场额外补偿约59.1万元，补偿后所有机组利润均不低于常规调峰阶段利润，保证其调峰主动性，火电机组才会倾向于参加投油深度调峰。

3）调峰补偿对比。

将市场报价和最大相对满意度两种补偿模式进行对比，结果如图12和图13所示。

通过对比可知，无论火电机组处于哪种调峰阶段，最大相对满意度补偿策略均能保证机组参与深度调峰后的利润不低于常规调峰阶段的利润。然而在市场报价模式下，机组不同档位价格上限的限制使火电机组在该补偿模式下并不能保证收回基本成本，因此火电机组参与深度调峰的积极性无法被充分调动。

5 结论

为鼓励火电机组主动参与深度调峰，本文在考虑火电机组不同程度的调峰成本基础上，建立了以火电机组总发电成本最小为目标的电力系统经济调度模型，并对深度调峰后的火电机组进行补偿。得到如下结论。

1）对于大规模风电并网的电力系统，火电机组参与一定程度的不投油深度调峰能获得更好的经济效益。由于机组出力的减少和损耗成本的增加，火电机组净收益减少，需要对火电机组进行深度调峰交易补偿以提高其参与深度调峰的积极性。相较于当前市场报价模式补偿，提出的最大相对满意度补偿能保证火电机组参与深度调峰后净收益高于常规调峰阶段净收益，满足调峰主动性约束，调峰机组乐于参加不投油深度调峰。

2）火电机组进入投油深度调峰后，昂贵的投油成本使系统成本剧增，并成为系统运行成本的主要组成部分。为提高系统运行经济性，有必要减少大容量机组进入投油深度调峰阶段的时间，以减少系统总油耗成本。尽管在投油深度调峰阶段风电场收益增加，但系统净利润却低于常规调峰阶段，此时火电机组收益剧减，不满足调峰主动性约束。

3）当前调峰市场的机组报价模式中，梯度报价的上限决定了机组所获补偿的上限，无法充分保证其参与深度调峰时的成本回收。基于合作博弈的最大相对满意度补偿策略考虑了机组对调峰补偿的倾向度，能直观反映机组参与深度调峰的意愿，并保证其参与调峰的主动性。本文所提方法能为当前火电机组补偿机制提供一定程度的借鉴。

4）火电机组参与投油深度调峰时，需在调峰市场外对其进行额外的补偿，保证其调峰主动性。结合中国当前碳交易和绿证交易的发展趋势，未来可将调峰市场与碳市场等结合，在促进风电等新能源消纳的前提下激励火电机组积极参与深度调峰。