城市道路超车特征分析与高风险超车识别
2022-10-08李君羡沈宙彪吴志周
李君羡,王 浩,沈宙彪,吴志周
(1. 同济大学道路与交通工程教育部重点实验室,上海 201804;2. 上海应用技术大学计算机科学与信息工程学院,上海 200235;3. 上海市城市建设设计研究总院(集团)有限公司,上海 200125)
超车是影响道路交通安全和效率的重要因素[1],量化描述超车过程、识别高风险超车对提升道路安全、增进交通管理效率有重要意义。
超车涉及2 辆甚至多辆车辆的复杂互动过程,许多学者通过分解该过程开展研究:柏伟等[2]基于车辆跟驰过程中的车辆互动关系建立超车模型,详细描述了不同超车阶段车辆的距离变化;Jenkins等[3]根据超车加、减速的行为分别将超车的开始和结束分为多类,并逐类讨论其特征;Zhao等[4]引入区间分析法探讨最小超车安全距离的影响因素,并以高斯伪谱方法将最优控制问题转化为非线性规划问题求解以描述超车过程;张文会等[5]将双车道公路场景下的超车划分为多个时段,继而分别分析了各种车辆与被超车、对向车的安全距离。
上述成果从微观层面研究主超车与被超车的具体行为,强调复现单次超车的完整过程。由于超车可能涉及除主超车与被超车以外的其他主体,故以上模型变量关系复杂,求解也多有明显的模糊性;此外,单次超车在路段中可能密集发生多次,且涉及主体类型多样。因此,从微观行为切入研究路段上的全部超车行为特征及风险可能导致组合爆炸,无法满足实时分析要求。鉴于此,许多学者转而提出从中观层次考察路段上超车行为的统计特征:荣建等[6]以仿真为工具,分析了等速、加速超车模型中主超车与被超车的速度变化,拟合了双车道公路的超车率与流量的关系;Qin 等[7]提出关键决策点的概念,认为在双车道公路场景下,若干个关键位置的多重决策共同决定了超车行为的结果;Lu[8]定义了表征公路运行特征的拥挤概率、自由行驶概率、车辆进入概率等指标,研究双车道公路上自由超车规则对公路通行安全及效率的影响。
以上针对超车对路段整体影响的研究对路网交通管理有指导意义,但此类研究多聚焦在公路场景。鉴于城市地面道路交通的间断流特性,驾驶员超车目的和行为必然与之不同,故前述研究结论难以为城市道路管理所借鉴。目前针对城市道路上非机动车或机非交互超车有较丰富的研究成果[9-10],但针对机动车专用道超车的中观描述指标及总体行为特征分析较为有限:秦雅琴等[11]构造超车次率指标,建立某指定路段上该指标与流量、平均速度和平均行程时间在不同场景下的拟合关系;王浩等[12]利用GRU网络实现对城市路段超车率的预测。上述研究对城市道路超车的独有特征解释不足;涉及的指标比较单一,反映出超车行为的特征较少,也无法很好地支持风险分析;研究中拟合定量关系时仅基于唯一路段数据,缺乏对普遍规律的讨论。
综上,从中观层面描述城市道路路段上的超车行为统计特征及其与路段交通运行特征参数的关系,可有效降低分析的复杂度,也能为城市道路交通管理提供直接依据;而对城市道路超车特征的讨论也有待深入。本文以此为切入点,在分析城市路段超车过程特征的基础上,构建描述这些特征的多维度中观指标,利用多条路段的车牌识别(license plate recognition,LPR)数据实现上述指标群的实时计算,并将其用于路段高风险超车的在线识别。
1 城市路段超车类型分析
在城市路网中,超车不仅与主超车和被超车的行为以及所在路段长度、限速、流量有关,还受到管控措施的影响。在同一外部环境下,即使各项微观指标都相同的超车行为,由于主超车出发时间与上下游交叉口信控方案对应关系不同,超车过程也可能存在差异。考虑交通波理论体系成熟、展示直观等优势,以其为工具解释导致该差异的原因。根据该理论,路段交通运行过程可抽象表示为图1[13-14]。假设不考虑交叉口排队溢出情况,排队车辆可在下一个周期绿灯期间完全疏散,且所有未超车车辆的路段平均行驶速度相等且小于路段限速。以上假设可根据实际情况深化调整,不影响过程分析的有效性。

图1 不同出发时间对应超车过程示意Fig.1 Diagram of overtaking processes with different departure times
图1中,长度为dL的路段L连接两相邻交叉口α与β,现有若干车辆由α经过L向β行驶。落在y=dL水平线上的粗实线段Sr表示交叉口β处与这股交通流对应的红灯期间车辆在此期间内积累排队。参考排队形成波速和消散波速,可结合Sr唯一确定各周期的“排队三角”,从而描述排队形成与消散过程。图1 包含了3 对超车共6 辆过车(B车超过A车、D车超过C车、F车超过E车)的时刻-位置曲线。除主超车和被超车的实际曲线外,图中还给出了主超车按照路段平均行驶速度行驶、并未超车的假想曲线(简称“计划曲线”,对应状态称为“计划状态”)。
图1 中,3 对超车的出发时间差、主超车与被超车各自的平均行驶速度均相同,但主超车在该路段上的行程时间减少程度不同:其中F车超过E车的情况较常见,两者均不停车通过交叉口β,F车通过超车所节约的行程时间ΔtF完全由其计划状态速度和实际速度的差值决定;D车虽超过C车,但在交叉口β加入了排队队尾,超车所节约的行程时间ΔtD因排队时车头时距被压缩而减少,获益最小;B车因超过A车赶在交叉口β红灯期间前通过,避免了交叉口排队延误,比计划状态节约了ΔtB的时间,获益最大。以上第2、3 种超车反映了城市道路特有的、超车获益被信号控制所影响的现象。事实上,许多驾驶员为实现第3种超车会在路段行程中有意识地提高速度,引发较高风险,值得关注。下文分析中称第3 种超车为“高收益超车”,称第1、2 种超车为“一般超车”。
可见,类似的超车行为对主超车的行程速度提升效用可能存在差别,这是城市路段超车的显著不同于公路超车之处。仅以超车数量或次数作为描述指标则不足以反映这一特征,因此需构建更多指标。
2 城市道路超车特征描述指标

(1)路段超车数nT:指定时段T内V′i的计数,为时段集计量。
(2)单车超车幅度nV′i:任意V′i驶过L时,其通过超车所实现的车队序列的提前程度为
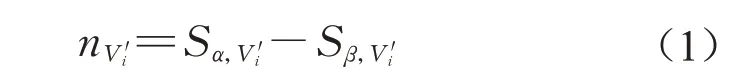
其中,Sα,V′i、Sβ,V′i分别为V′i通过α和β时在车队中的次序,对任意V′i均有nV′i>0。对指定时段T,可集计时段超车幅度总和nQ,T,如式(2):

上述指标中,nT和nQ,T综合表征了指定时段内的路段L上超车发生的频繁程度,两者能间接反映超车行为对路段的影响,其数值的异常波动可能预示着有特殊事件发生;nV′i、ΔvV′i和vA,V′i则从各方面间接体现单个V′i通过路段时的超车风险;BV′i衡量了单个V′i在L上超车的获益,由BV′i可初步区分高收益超车和一般超车,将之与vA,V′i、Sα,V′i结合可揭示超车意图,便于实时查找以高速甚至超速超车以获取高收益的车辆,实现对车辆或路段的管理。
为实时标定以上指标,需具备较高时间颗粒度采集的、连续经过2个交叉口的所有过车信息,并能唯一识别各个车辆,LPR数据可满足该要求。
3 基于LPR数据的指标计算
LPR数据多由视频设备采集并上传,原理如下:车辆进入设备初始设定的虚拟线圈位置,触发设备采集标准化图像。对图像进行信息提取与结构化压缩,可将其转化为逐条的过车LPR 文本数据,包括车牌、时间戳、车辆类型等关键信息。LPR数据颗粒度高、压缩后存储成本低,基于多个设备车牌碰撞还可实现车辆路径跟踪。
为研究指定路段的超车特征,需结合其上下游2个交叉口的各向LPR 数据。沿用前文标记,为研究在交叉口α 直行进入路段L并于交叉口β直行离开的车辆群体超车行为,需对α、β分别采集到的LPR数据集Φα、Φβ预处理,如下:
(1)数据清洗。仅保留LPR 数据的车牌、时间戳2 个字段;剔除无法支持车牌碰撞的无车牌数据及有明显时间戳录入错误的数据。
(2)确定目标车道组。在α、β处不同相位放行的车辆,其进入、离开L的时间受信控相序的强制干扰,无法进行超车比较,故要求研究的车辆样本群应在α、β处分别属于同一车道组,即在相同相位进入、相同相位离开L。
(3)提取目标车道组有效数据。根据目标车道组所对应的交叉口分支与车道编号过滤Φα、Φβ,仅保留相关样本,分别构成压缩数据集Φ′α、Φ′β。
(4)匹配路段过车记录。对Φ′α所有车牌去重,构成出发车牌集合P,遍历P碰撞比对Φ′β,匹配同一辆车先后出现在2个集合中的记录,按照图2所示规则组织字段,对每一次过车Vi生成1 条路段过车记录ri。若同一车牌有多次匹配记录,则应分别保存。将所有记录汇聚为路段L的过车记录集合RL。
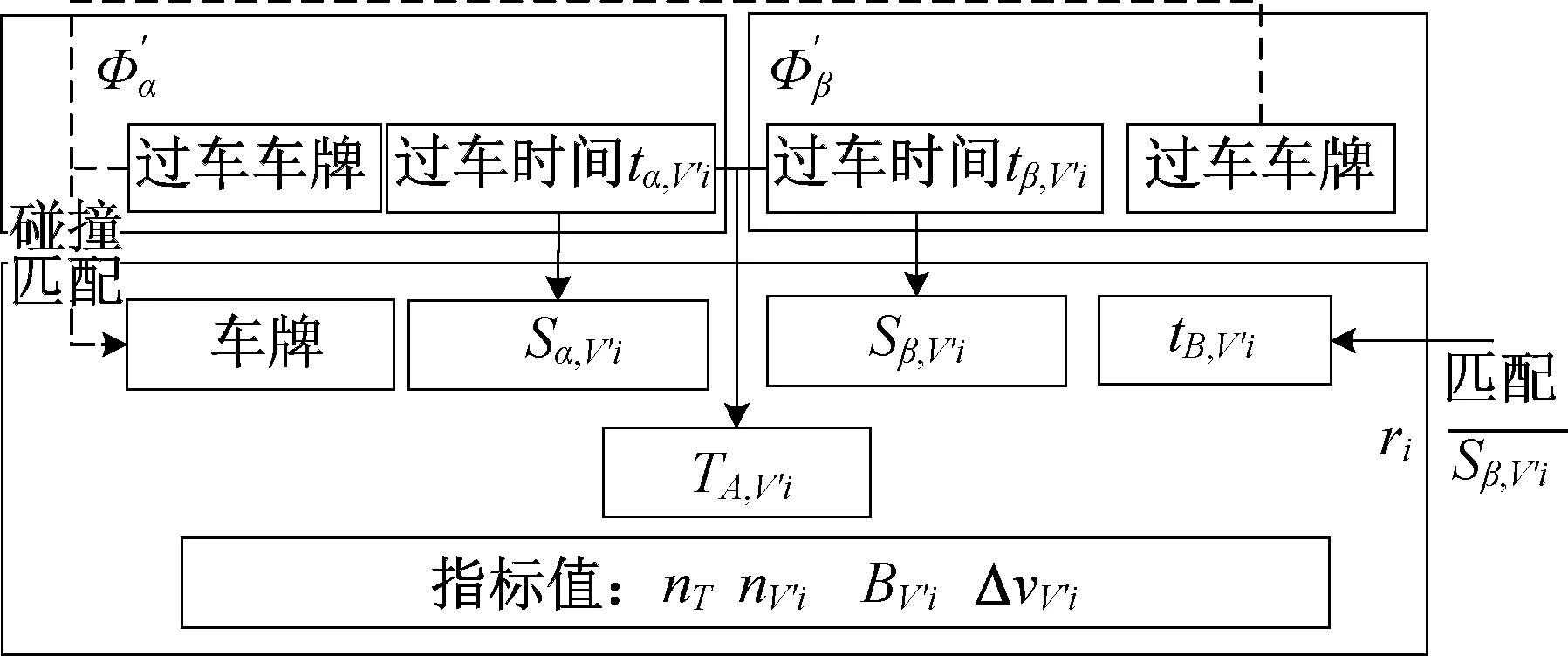
图2 单条过车记录字段组成Fig.2 Attributions of a single passing record
(5)将RL按照tβ,V′i先后排序,由1递增按序赋值每条记录的Sβ,V′i;再将RL按照tα,V′i先后排序,由1 递增按序赋值每条记录的Sα,V′i。

综合上述属性,可根据式(1)—(3)及式(8)计算ri的各项指标,并对指定时间段计算指标集计值。在此过程中,需根据BV′i值剔除有明显长时间停车行为的车辆,以避免对超车分析的干扰。
4 实验与结果分析
4.1 数据描述与处理
以某城市主干道上连续4个信控交叉口及其双向连接共6个路段作为研究对象,各要素关系如图3所示。路段全线限速60 km·h-1(16.5 m·s-1),各交叉口进口道均布设电子警察以采集LPR 数据,虚拟线圈设置在停车线位置,即LPR 的时间戳对应过车车头通过停车线的时刻。
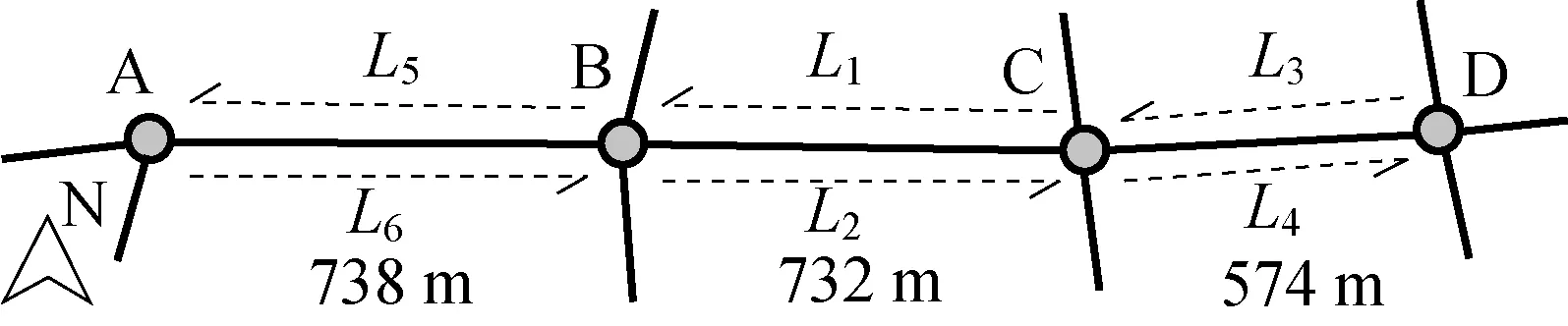
图3 示例交叉口及路段关系示意Fig.3 Sample intersections and road section relationship
收集2018 年7 月6 日各交叉口全量LPR 数据,并参照第3节步骤进行处理,具体细节包括:
(1)确定研究对象为由西直行向东继续直行、由东直行向西继续直行的车道组,即要求对于6 条路段而言,均有dα=dβ=直行。根据选定车道组过滤并清洗数据,生成各交叉口过滤数据集Φ′Y(Y∈{A,B,C,D})。
(2)依次计算各路段过车记录集合RZ(Z∈[1,6]),根据RZ对应的路段长度,结合路段限速约束路段行程时间范围,行程时间超出该范围的过车可能离开路段、长时间停车或时间戳录入有误,不适于作为研究样本,予以剔除。
4.2 实验结果与分析
4.2.1 路段整体超车分析
按5 min 间隔集计全日各路段的n5min、nQ,5min指标,分析其与对应时段流量V5min关系,如图4。
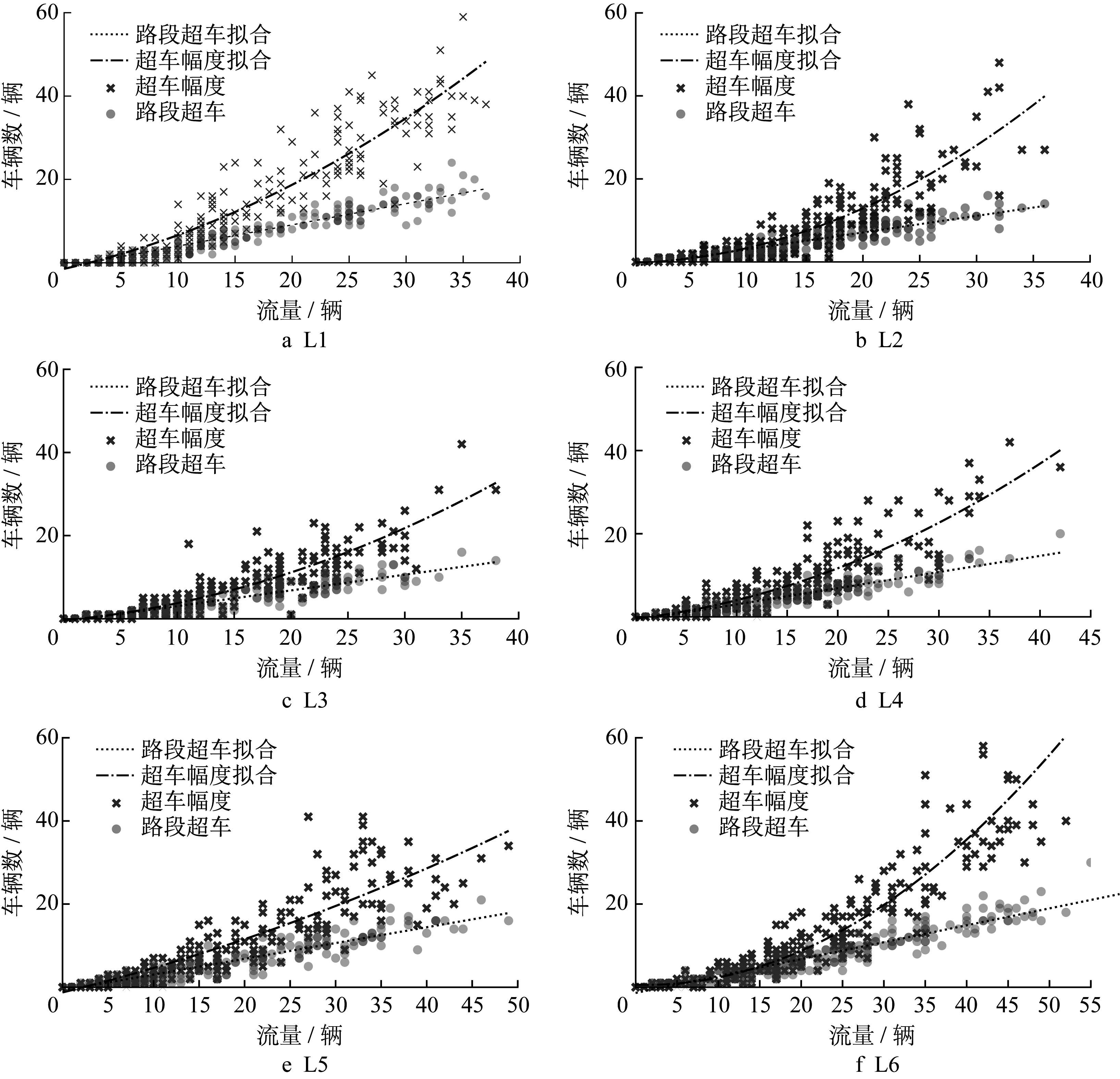
图4 指标n5min、nQ,5min与流量V5min关系分析Fig.4 Correlativity between n5min,nQ,5min,and volume V5min
由图4 可知,在路段流量不饱和条件下,n5min、nQ,5min均与V5min呈正相关关系。拟合结果表明,2 组相关关系分别可以有界的一次和二次多项式拟合。对6 条样本路段,n5min的一次拟合系数均稳定在[0.37,0.40]区间,各子图相应曲线斜率相近;而nQ,5min与V5min的关系则因路段不同有显著差异,其中L1 和L6 的nQ,5min-V5min曲线最陡峭,意味着路段集计超车幅度总和对流量增长更敏感;在同等流量条件下,这2 个路段的超车行为相对更加冒进。以上差异说明,城市道路的超车次数特性因路段而异,应根据真实数据逐一拟合,对于超车频次统计量对流量敏感的路段应进行重点管理。
4.2.2 超车速度变化与分布特征
除超车次数与幅度指标,超车的速度特性也会影响路段安全,且能反映超车车辆对路段运行的影响。分析时需参考路段限速vlim=16.5 m·s-1,并根据管理需求定义路段的临界速度vth作为路段高速车辆的界定标准,设定vth=0.85×vlim=14.0 m·s-1。
首先考察各主超车的vB,V′i、vA,V′i与ΔvV′i的关系。以L2和L6为例,分析结果如图5。
vB,V′i-ΔvV′i散点图有明显的分组聚集特征,尝试以K-means算法对样本点自动聚类。首先采用组内平方误差和(sum of squared error,SSE)指标辅助算法定参[15],结果显示对于2个样本路段,均有聚类数目K=3时效果最理想。按照此参数聚类并计算类别中心坐标,结果见图5a、5c;然后保持原有聚类结果的标签,按照相同图例绘制各主超车的vA,V′i-ΔvV′i散点图,对比计划状态与实际状态的速度散点图,可知:
(1)低vB,V′i的主超车如果没有超车,其聚类速度中心将低于6.5 m·s-1,小于正常路段行驶速度。这表示其如按计划速度行驶,将在下游交叉口遇到红灯停车。
(2)在低vB,V′i车辆中,有部分样本超车后平均速度提升ΔvV′i高达8 m·s-1左右,构成了与其他2簇明显分离的簇(图5 中簇Ⅲ)。簇Ⅲ车辆经过超车加速,其vA,V′i转移至高速区,明显避免了下游交叉口停车排队,实现了一次性通过路段,即为高收益超车车辆。需注意,对于部分车辆有vA,V′i>vlim。
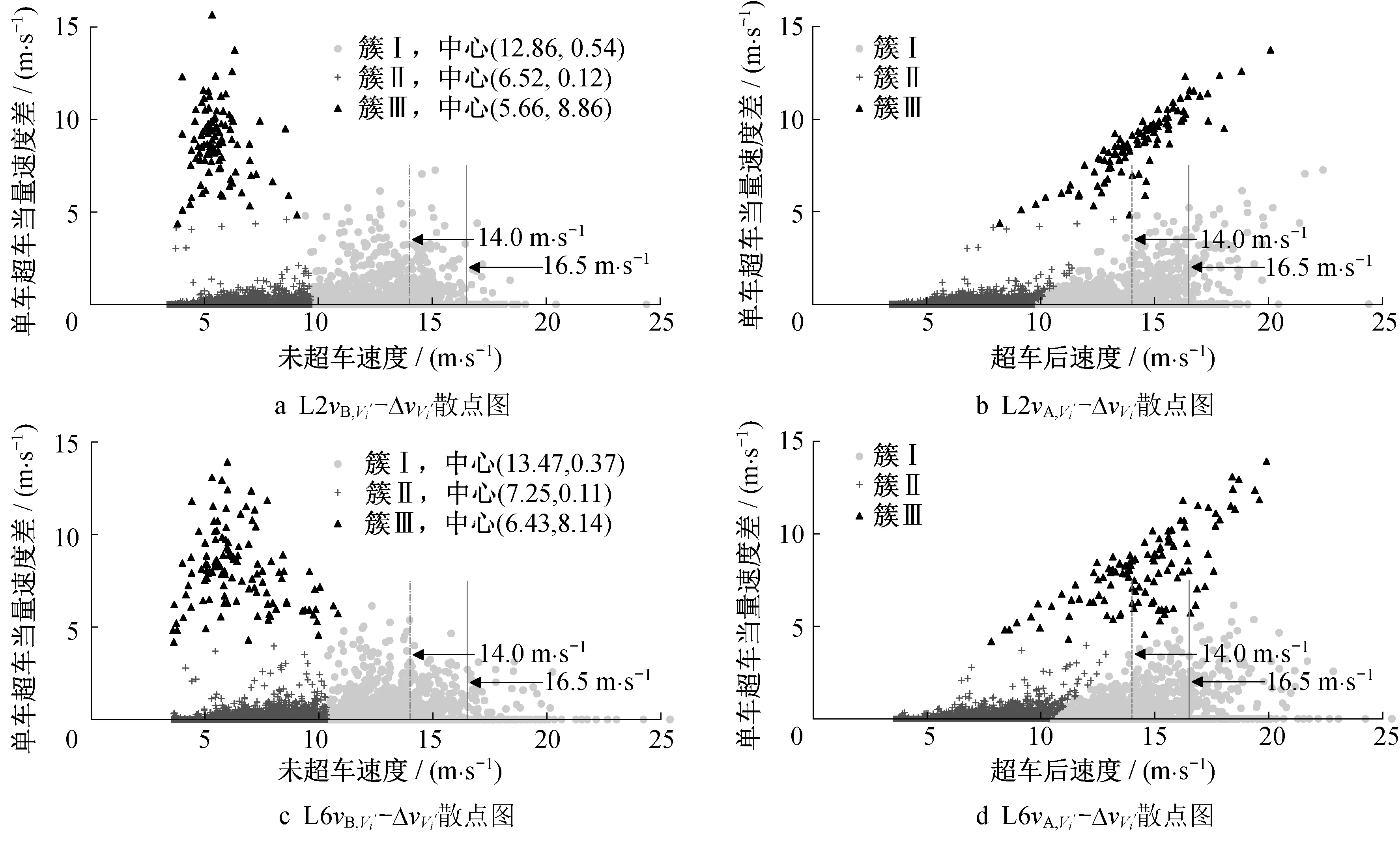
图5 示例路段vB,V′i、vA,V′i与ΔvV′i散点图及聚类结果Fig.5 vB,V′i-ΔvV′i and vA,V′i-ΔvV′iscatter diagrams of sample segments and clustering results
(3)与簇Ⅲ对比,部分同样低vB,V′i的车辆仅通过超车略微提升了行程速度(图5中的簇Ⅱ)。从其聚类中心来看,ΔvV′i<0.2 m·s-1,对应出发次序靠后、超车目的性较弱的一般超车,其超车后vA,V′i的聚集位置相对vB,V′i基本不变,只略微向右侧迁移。
(5)图5中簇Ⅰ聚类中心的X坐标值显著大于簇Ⅱ和簇Ⅲ,对应vB,V′i较高的样本群。即使按计划速度行驶,此类车辆也不会在下游交叉口遇到红灯,或在加入下游交叉口排队队尾较短时间后即跟驰通过。但当其有超车行为时,ΔvV′i比簇Ⅱ更大,vA,V′i相对vB,V′i右迁更明显,显示这类超车有更强的目的性,行为也更加冒进。虽由于路段限速等客观因素限制,簇I 车辆整体速度上浮空间有限,但也有部分车辆vA,V′i>vlim,存在一定风险。
上述规律在各样本路段中普遍存在。按vB,V′i行驶将明显受到信控影响而停车等待的车辆,其超车获益大、目的性强,贡献了最大的ΔvV′i,这部分车辆中,短时内完成加速超车或vA,V′i较大的车辆存在较高风险,故还需结合超车时机以及vA,V′i观察。仍以L2和L6为例,图6由不同行程速度区间的样本量转移,更直观地体现了超车所导致的路段整体速度分布变化。

图6 示例路段有无超车速度分布对比Fig.6 Speed comparisons of sample segments with and without overtaking
根据图6,超车行为对中段区间速度分布影响较小,主要的变化体现为原低速区车辆转移到高速区,尤其是超过vth的车辆明显增加,这与簇Ⅲ车辆的较大速度变化以及簇Ⅰ车辆进一步提速有关。如前分析,这部分车辆的超车行为可能增加路段的安全风险,需结合vA,V′i和ΔvV′i对其重点分析。
4.2.3 高风险车辆分析
根据vA,V′i将超车车辆划分为vA,V′i≤vth的低速车辆、vlim≥vA,V′i≥vth的高速车辆和vA,V′i≥vlim的超速车辆3 类,3 类车辆的路段行程风险依次增加,以下结合超车风险及收益情形详细分析。如第1部分所述,因车辆出发和到达上下游交叉口的时刻与信控方案对应关系不同,ΔvV′i和BV′i并非一一对应。以L1、L2、L5为例,绘制ΔvV′i-BV′i散点图,并以不同图例区分不同风险类型车辆,如图7。

图7 3类车辆ΔvV′i与BV′i关系分析Fig.7 Correlativity between ΔvV′i and BV′i for 3 types of vehicles
图7显示,由于信号配时方案和路段长度差异,不同路段超车车辆的收益上限也不同,但各类车辆的风险与收益关系有以下统一规律:

(2)低速车辆靠近原点有一处明显聚集,对应图5 中的簇Ⅱ,这部分车辆在超车后仍以较低速度行驶,其BV′i<20 s,属于一般收益车辆,其超车多与争抢绿灯末尾通过交叉口无关,对路段行车秩序影响有限。在低速车辆中,也有少部分超车收益较大,但这类数据点样本量较少且比较分散,且其超车增速后仍在低速区,影响相对可控。
(3)高速车辆普遍通过超车实现了一次性通过路段。相对低速车辆,其点集在X轴方向分布更加均匀,但在ΔvV′i=10 m·s-1附近有一处高密度聚集。对于3 条示例路段,此处的超车收益均值均大于70s,明显与车辆通过加速在下游绿灯通过有关,属于高收益车辆。此类主超车通过以较大的ΔvV′i达到较高的vA,V′i,虽然尚未超速,但速度变化幅度大,有一定不稳定性。
(4)超速车辆是路段交通管理中的重点。样本路段的超速车辆均明显地分为2 组,分别对应较高和较低的ΔvV′i,如各子图中i 和ii 标示的部分。这2组车辆的组间距较大,其间以ΔvV′i∈[4,8]m·s-1的幅度超车以致超车后速度超限的车辆较少,多数在超车后超速的车辆或本就已经超速(ΔvV′i较小),或有目的地提升速度并超车以争取更多利益(ΔvV′i较大)。前者对应的是驾驶行为较为冒进的车辆,后者则对应大幅加速以争取在下游绿灯结束前通过的车辆,两者对交通运行均有严重的影响,而后者的速度还伴随不稳定特征,其超速行为更可能集中在路段后半行程,属于高危超车行为车辆,需要加强管制。
可见,vA,V′i和ΔvV′i较大的主超车车辆都是路段超车管理所需关注的重点,且其与上下游交叉口信控方案的协调有一定关系,以下展开分析。
4.2.4 高风险超车与信号方案关系分析
按照Ban 等[16]的研究,路段行程速度及延误等同时受上下游交叉口信控配时方案及其协同设计影响,在各周期车辆可完全疏散的理想假设下,上游同周期放行车辆的行程速度逐渐增加、延误逐渐减小。图8为L1和L2这2条路段的所有车辆vA,V′i-tα,V′i散点图,其中无超车车辆的速度称为“稳定速度”,以实心圆点表示;有超车车辆的计划、超车后实际速度称为“超车前/后速度”,分别用向上三角形和向下箭头表示,并以虚线将ΔvV′i>10 m·s-1的成对标记相连。按照行程速度分布曲线,可设置一个分位数速度vs作为低速车辆的界定标准,本文以15%分位数为例,在图8 绘出vlim=16.5 m·s-1和vs这2 条水平线以便对比。
图8除了显示出文献[16]所描述的单周期行程速度变化趋势外,更揭示了多个连续周期在更长时间轴上的行程速度周期性变化现象。这种周期性由相邻交叉口的协调相位差引起,且因相邻交叉口信控周期时长关系不同呈现不同的循环间隔和波动。结合以上2 类周期性,观察图8a、8b 可知,在两交叉口相位差协调情况较好的周期,绝大部分同相位放行车辆可以大于vs的速度通过路段,此时vA,V′i和ΔvV′i较大的高风险超车明显减少。但由于一般相邻交叉口并无绿波协调设计,较佳通行状态通常仅能维持少数几个周期,随后进入最不利协调周期时,对绝大部分过车有vB,V′i<vs,此时高ΔvV′i值超车迅速增加。可见,高风险超车多发于相邻交叉口信控配时协调导致上游交叉口整个周期过车平均速度全部较低的周期。
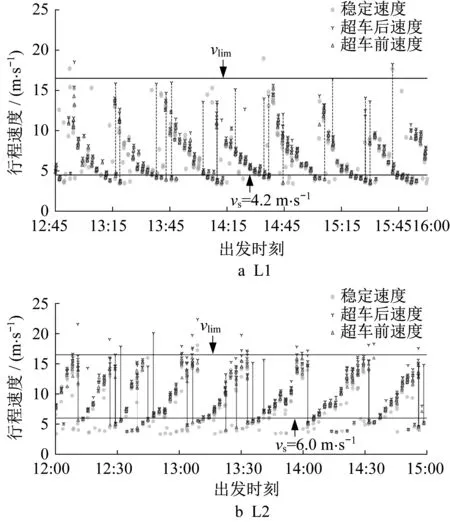
图8 高风险超车速度特性分析Fig.8 Speed characteristics of high-risk overtaking
图8b中,92%的超速车辆由vB,V′i<vs的低速车辆通过加速超车转化而来;而2 个示例路段上ΔvV′i>10 m·s-1的车辆中,90%的车辆有vB,V′i<vs。在计划速度提升到接近vs时,超车后超速以及高速度变化等风险较高的超车数量就有明显下降。这提示加强相邻交叉口信号控制协调除了可以增加绿波带宽度、使得更多车辆不停车通过路段外,更对减少不安全超车行为有一定作用,即使并非协调控制的交叉口群,合理调整主要流向的相序或微调其放行相位的绿信比,保证大部分车辆的行程速度,都有助于改善超车对路段交通的不利影响。
为观察高风险超车频发时段的vA,V′i-tα,V′i关系,进一步放大时间轴绘图,图9a、9b 分别为取自L5 和L6的示例时段。
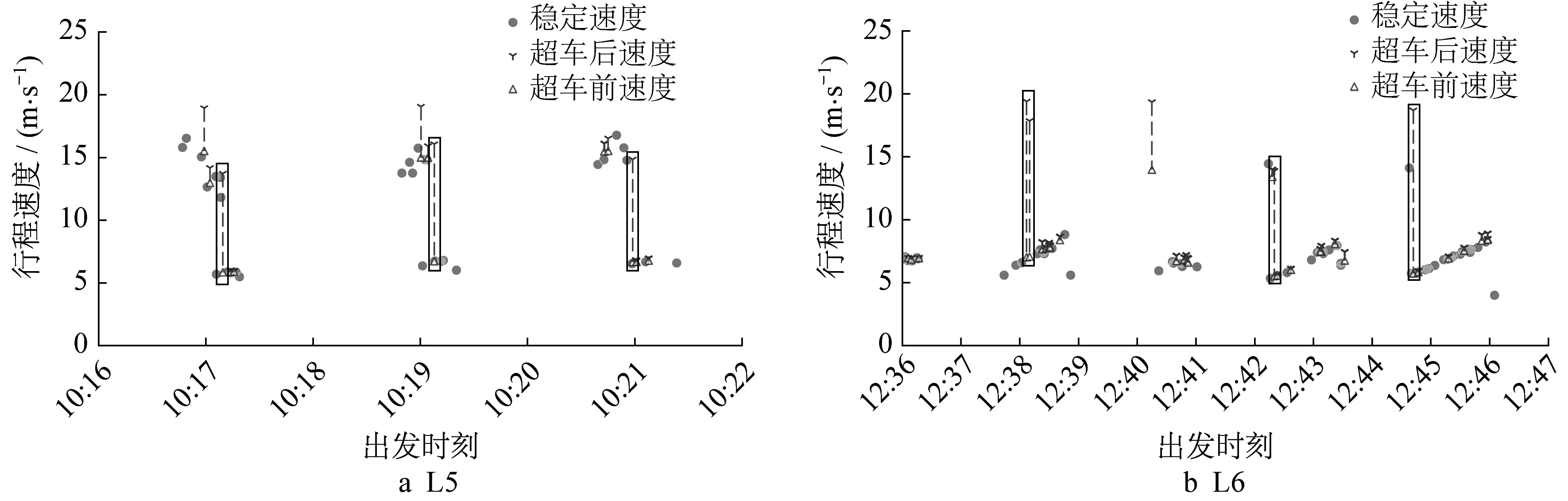
Fig.9 高风险超车车辆在上游交叉口车队中的序列Fig.9 Sequences of high-risk overtaking vehicles at upstream intersection
图9a 所显示的3 个连续周期中,部分车辆以接近15 m·s-1的vA,V′i不停车通过路段,这些车辆中,出发时刻最晚的少数几辆车均是ΔvV′i值接近10 m·s-1的主超车(图9a 框选部分)。因上下游相位协调问题,跟随这些主超车之后的车辆则因无法顺利超车或提高速度,在下游交叉口红灯期间到达,需要多等待1 个周期才能驶离路段,其vA,V′i仅为5 m·s-1左右。可见,当路段上游交叉口同一相位放行的交通流在下游交叉口被红灯部分阻断时,下游交叉口绿灯末尾常见高风险超车。
区别于图9a,图9b 所示的几个连续周期中,因上下游相位协调十分不利,几乎全部车辆按计划速度行驶都将在下游交叉口停车等待,如前分析,此类周期常发高风险超车。图9b显示,这些高风险超车多发于上游交叉口相应相位的放行初期(图9b框选部分),这是由于车辆行驶在车队队首时,受前方和侧向车辆约束较小,超车难度也最小。
综上,当相邻交叉口的信号控制方案及协调情况确定后,高风险超车高发时段呈现明显规律性并可提前根据信控方案具体预测,为管理路段上的高风险超车和超速运行提供了依据。
5 结语
以交通波理论分析了城市路段超车特征,并构建多维度中观指标体系对其加以描述。以真实LPR数据实现各指标的实时计算,并讨论了基于该指标体系识别、预测高风险超车的方法,主要结论包括:
(1)城市道路超车的特征在于其收益受上下游交叉口信控配时协调的影响。为体现这一特征,应构建涵盖超车频次、超车速度、超车收益等多方面特征的指标体系。
(2)在一定时段内,路段超车次数和超车幅度总和与流量的关系可分别以有界的一次、二次多项式拟合,可由此识别超车行为对流量高敏感的路段并重点关注。
(3)可根据主超车的计划行程速度和单车超车当量速度将其聚类为3种类型;根据主超车的类型,结合其超车后行程速度和单车超车当量速度差可识别路段高风险超车车辆。
(4)高风险超车多发于因相邻交叉口信控协调不利导致的全部车辆低速行驶的周期;其常见于下游交叉口绿灯末期;如上游交叉口全周期车辆低速行驶,则周期初放行车辆更倾向于高速超车。
作者贡献声明:
李君羡:论文构思,方法论提出,算法编程,可视化呈现,初稿写作。
王 浩:论文构思,校验。
沈宙彪:形式分析,审核与编辑写作。
吴志周:获取资助,项目管理,指导。
