在亳州药都背景下对高中数学校本课程的探究
——以皖北协作区高三联考试题为例
2022-10-08吴孝强张侠飞
吴孝强 张侠飞
(亳州市第三十二中学 安徽亳州 236800)
引言
开发校本教材和校本课程对促进教师成长和提高教学质量有着十分重要的意义。亳州是一个具有3 700年历史的文化名城,在种植药材、开发中药、传播中医药文化方面有着独特的优势和作用,对特色校本课程开发具有重要的作用。
一、校本课程探究的背景
亳州作为历史悠久的“中华药都”,是全国中药材集散地,以建安路为纽带,建设了诸多的药材市场,如康美、神农谷、太安堂等药材市场,每年仅药材销售额就达一百亿元之多。同时中药材种植带动当地经济发展,全市有四百多个药材品种,八百多个药材种植基地,药材种植面积达六十五万亩。药材业已经成为亳州的主要经济支柱。亳州是一代名医华佗的故乡,是中医药文化的发源地,早在明清时期,亳州就是全国四大药都之一,现在更是建设成为“中国药材第一市”。
基于亳州的中医药特色,高中的很多学科在校本课程的开发过程中大有所为,依据新时代教育的要求,积极投入其中,以每个学科的特点和内容为基础开展相关研究,一定能开发出具有地域特色和学校特色的校本教材和校本课程。
二、对皖北协作区试题的研究
2022年3月25日至26日亳州一中作为主办单位,举办了“安徽省示范高中皖北协作区”第24届高三联考,在数学和理综的试卷中出现了大量以亳州中医药为背景的试题。笔者对这些试题进行整理,并结合学校特色课程,对该次联考试题进行分析、总结,为开发具有地域特色的校本课程整理了一些思路。
例如数学选择题第5题:有诗云:“芍药乘春宠,何曾羡牡丹。”芍药花不仅具有很强的观赏性,而且具有药用价值。某地打造了以芍药为主的花海大世界,其中一片花海是正方形,它的四个角的白色部分都是以正方形的顶点为圆心,正方形边长的一半为半径的圆弧与正方形的边所围成的(如图1所示)。白色部分种植白芍,中间阴影部分种植红芍。倘若你置身此正方形花海之中,则恰好处在红芍中的概率是( )
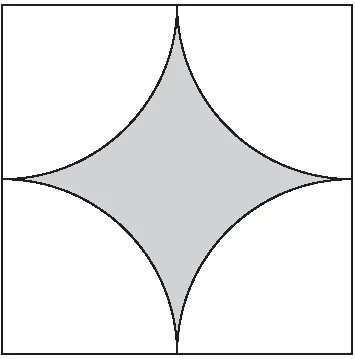
图1

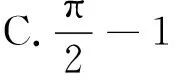
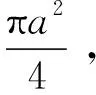
总结:(1)亳州白芍药产自谯城区,每年9-10月采挖,3~5年生根,在我校学生居住的村庄就有种植芍药的,甚至学生自家就种植了芍药,因而学生见到此题后倍感亲切,结合自己所学的知识,可以轻车熟路地解决这个问题。熟悉的题干背景有利于学生提炼数学知识,运用知识解决问题。(2)本题考查几何概型的概率求法,题型设置上符合新高考对知识的要求,达到了考查学生的基本知识掌握情况的目的。(3)此次联考有16个地、市近百余所学校参加,涉及范围广、影响大,对弘扬亳州中医药文化、传播中医药知识有重要的意义。(4)作为主办方的亳州一中也彰显了传承中华文化的重要性,努力培养出“药都印 中国心 天下人”的优秀学生。
三、触类旁通,对具有地域特色的校本课程的开发
由以上联考题,我们可以自行开发具有地域特色的校本课程,比如利用线性回归方程探究亳州特产中药亳菊花的散热解毒的药性。通过研究,我们得到了以下数据,利用这些数据帮我们解决生产和生活中的一些具体问题。
例如:亳菊、滁菊、贡菊和杭菊被称为中国四大“名菊”,亳菊是地道的中药材,有清热解毒、散风清热的功效,为了更好地研究亳菊的药用价值,我们对亳菊的储存时间和药性进行了实验,对药性损失率(%)与储存时间(单位:年)之间的关系进行了统计分析,得到一组检测数据如表1所示:
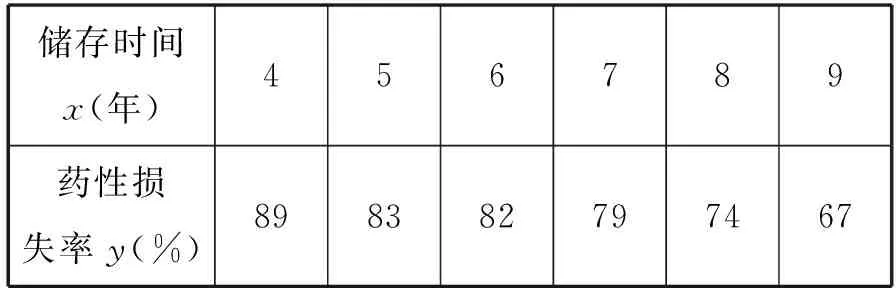
表1
(1)若与之间的关系可以用线性回归模型拟合,现通过、、三种解决方案求得回归直线方程分别为=-4+105,=4+53和=-3+104,其中有且仅有一种方案的计算结果是正确的,请结合统计学的相关知识,判断哪种方案的计算结果是正确的,并说明理由;
(2)若用=++近似地表示与之间的关系,可以得到的回归方程为=-0375+0875+9025,经计算可知,和(1)中正确的线性回归模型的相关系数分别为0.9702和0.9524,请用说明哪个回归模型的拟合效果更好。
总结:
1.这是典型的以亳州特色中药材亳菊的药性研究为背景,进行回归分析的一道数学题,通过对这道题目的研究,促进了学生对亳菊的深入了解。
2.从对学生知识的考查层面上讲,一方面要求学生掌握线性回归方程的求法,求得一次项系数b和常数项a;另一方面要求学生了解相关系数和误差的关系,相关系数的取值范围为[0,1],越接近1,误差越小,曲线拟合的效果越好,程度越高。反之,越接近0,误差越大,曲线拟合的效果越差,程度越低。如果=1,说明描述的这些点(,)全部在直线上;如果=0,说明描述的这些点(,)非线性相关。
四、举一反三,在课堂情境设置中注入亳州中药材元素
例如:桔梗作为常用药材之一,有祛痰排脓、抗炎消菌、稳定血糖的作用,在2016年亳州市谯城区十八里镇就成立了桔梗种植基地。桔梗的种植条件要求并不高且幼苗耐寒,怕水涝。为了更好地研究桔梗的发芽率,基地进行了在相同条件下的发芽试验,结果如表2所示:
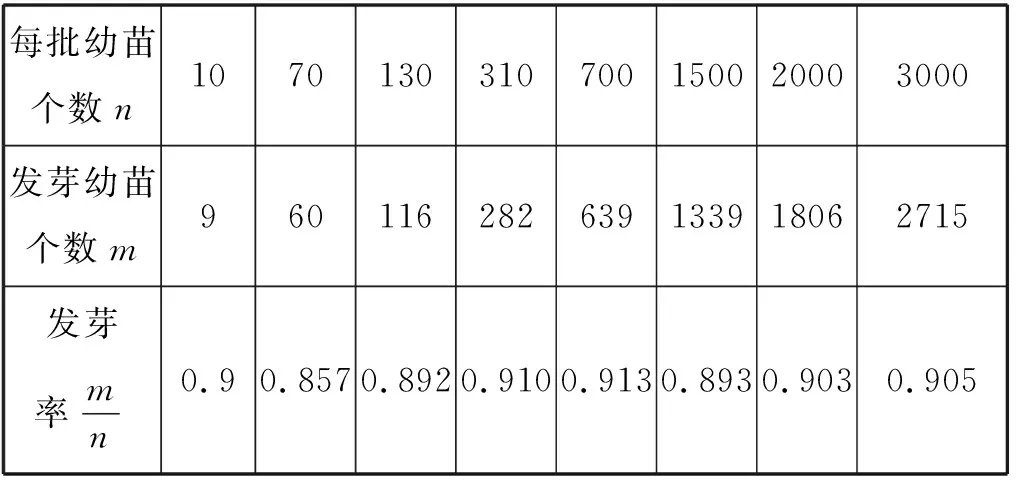
表2
学生活动:观察试验数据并计算桔梗发芽率,根据发芽率的变化规律,总结出:当试验的桔梗很多时,桔梗发芽率在常数0.9附近波动且逐渐趋于稳定。
教师活动及知识归纳:
(2)各组数据的频率不相同,但是波动幅度随实验次数的增加在变小。
综合以上的学生观察结果和教师的知识归纳,最后在设置的新课情境中很轻松地就得到了概率的定义。
教师知识拓展:
(1)大量重复的实验是得到概率的前提,是得到稳定值的条件。
(2)频率趋于稳定的值才是事件A的概率。
(3)频率和概率的关系:频率是变化的,每一次随着试验次数的不同而发生变化;概率不随实验的次数改变。
(4)在随机实验中,概率反映了事件发生的可能性大小。
(5)事件A的概率取值范围:0≤()≤1。
总结:
1.设置亳州特产中药材桔梗这一情境导入新课,目的是引入这节概念课的主题“频率与概率”。
2.亳州是全国最大的药材集散地,而桔梗的药用价值已经被市场充分认可,该地区由于气候适宜,所以种植了大量的桔梗。桔梗作为当地种植面积较大的药材品种之一,市场需求很大,所以研究桔梗的出芽率很有必要。
新时代要贯彻党的教育方针,就是要坚持立德树人,坚持五育并举,培养全面发展的时代新人。学校要跟上时代步伐,积极立足本地特色办人民满意的教育。亳州的特色是中医药,学校要办出特色就要与之相结合,形成具有地域特色的校本教材。学校要把德育、智育、体育、美育、劳育与中医药校本课程结合起来,形成学校的特色项目,进而办出学校的特色。
