课后服务课程:“数学与美”课程设计与实践
2022-10-07武成彬
武成彬 李 勇
(徐州市桃园路小学,江苏 徐州 221001)
学生对美的事物总是易于接受,而数学本身就存在美,并几乎与所有美的事物有联系,它是一种理性的美,是一种典型的“内在美”。数学处处充满美的感受、美的鉴赏、美的创造、美的发现,这些构成了完整的数学美。数学美一直是指引数学家前进和奋斗的一盏明灯,数学美不仅能给学生带来一种美的享受,也对学生理性思维、思辨能力的提升,同时对学生智慧的启迪和潜在能动性与创造力的发展都有着不可替代的作用。数学中的这种美需要教师去引导、去挖掘、去开发。将美学、观念引入小学数学校本课程开发,对激发学生的数学学习兴趣、提升学生的审美能力等都是一种很好的尝试。
一、课程理念
庄子曰:“判天地之美,析万物之理。” 数学作为一种工具、思想、方法,其背后蕴含丰富的精神气质和美学价值。数学不仅是运算和推理的工具,还是表达和交流的语言,数学承载着思想和文化,是人类文明的重要组成部分。数学的“理性”和“感性”如车之两轮、鸟之两翼,对于人的全面发展非常重要。数学既能培养学生的理性精神,又能促进学生科学精神的形成。数学的学习让学生发展对美的感受性,培养学生对美的事物的情绪体验,形成正确的审美能力和表达美的能力。
《义务教育数学课程标准(2022 年版)》指出,设立跨学科主题学习活动,加强学科间相互关联,带动课程综合化实施,强化实践性要求。能够理解自然现象背后的数学原理,感悟数学的审美价值;形成对数学的好奇心与想象力,主动参与数学探究活动,发展创新意识。欣赏数学语言的简洁与优美,逐步养成用数学语言表达与交流的习惯,形成跨学科的应用意识与实践能力。在课程目标中明确了各学段对数学美的具体要求:第一学段是了解数学可以描述生活中的一些现象,感受数学与生活有密切联系,感受数学美。第二学段是在他人的鼓励和引导下,体验克服困难、解决问题的成就,体会数学的作用,体验数学美。第三学段是在解决问题的过程中,体验成功的乐趣,相信自己能够学好数学,感受数学的价值,体验并欣赏数学美。第四学段是在解决数学问题的过程中,能够克服困难,树立学好数学的信心,感受数学在实际生活中的应用,体会数学的价值,欣赏并尝试创造数学美。
二、课程目标
课程目标的确定,立足学生核心素养发展,集中体现数学与美课程的育人价值。
(1)在真实可信的情境中综合利用自己所学的知识解决问题,体验数学知识在以美育人时的共促作用。
(2)运用调查、制作及问卷、访谈等方法,引导学生参与收集信息、分析资料、发现问题、解决问题的全过程,能够提出合理的假设并验证结论,提高社会综合实践能力。
(3)鼓励学生通过查找文献、收集资料和信息筛选,形成学习成果并进行展示,提高综合应用能力和创造能力。
(4)在活动过程中,培养学生实事求是的态度,在批判质疑中培养求真的科学精神,在沟通交流中养成团结协作精神和创新意识。
三、课程内容
1. 模块一:启动“数学与美”课程,了解学生对数学美的认知
向学生介绍本课程的理念、课程目标以及课程评价,并通过多种形式了解学生对数学与美的认知情况(见表1)。

表1 “数学与美”课程
跨学科整合设计理念:以学习规划——手抄报为抓手,融合数学知识、数学思维、语文素养、艺术设计、信息技术学科,呈现内容清晰、形式丰富、可行性强、易分享的学习作品。
2. 模块二:文学中的数学美,体验数学的简洁美
(1)数学遇上诗歌。找寻包含“数数”“找规律”“拆字格”“合并同类项”“等差数列”等数学知识或特征的诗歌,通过数学知识—对应诗歌—抽象数学知识,体会数学的简洁美,引导学生体会抽象夸张的诗句与具体严谨的数字所共同构成的文学。
(2)数学遇上语言。通过具体案例让学生体会数学语言的简洁美,例如图形、公式、字母表示数等;文学作品中的简洁美,例如传统古文、名家名言等;艺术作品中的简洁美,例如素描、抽象派等(见表2)。

表2 文字中的数学美
跨学科整合设计理念:以表现性活动为核心,通过融合数学、语文、美术、科学等知识,通过数字诗词创作和作品的征集与编排活动,鼓励学生积极探索数学的简洁美,培养学生的审美情趣,提高学生发现美的能力。
如六年级跨学科作业“徐州速度”,语文学科教师带领学生收集并整理从1949 年至今,徐州市的交通工具变化、城市居民居住范围变化;体育学科教师带领学生测算人的步行速度;数学学科教师带领学生计算不同交通工具的行驶速度,并使用统计图表分析年代、行驶速度、居住范围的变化;美术学科教师带领学生绘制“徐州速度”主题宣传画。通过“速度”这一关键词,把数学中的路程速度时间概念,与徐州的城市、经济发展相结合,通过计算、绘画、手抄报、演讲、布展等形式,用数学的方式讲述徐州发展的故事,激发学生热爱家乡的情感。
3. 模块三:结构中的数学美,体验数学的对称美
课程内容包括中国古代、现代建筑欣赏与创作;自然界的对称美的发现;宏微观世界的对称美的欣赏(见表3)。
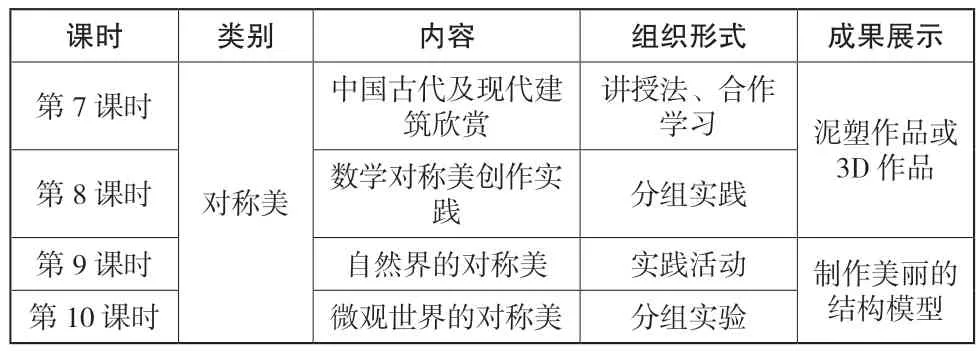
表3 结构中的数学美
跨学科整合设计理念:以动手实践为宗旨,融合数学、科学、美术、信息、劳动等学科,带领学生欣赏中国的古代及现代建筑,寻找自然界和微观世界的对称美,培养学生发现美和动手实验的能力,通过引导学生使用泥塑或3D 作品创作,设计学校的数学实验中心,培养学生动手实践和创造美的能力。
在五年级数学课程中,通过活动课程引入“泥塑中的数学图形”“泥塑中的黄金比例”“中国传统建筑的数学建模”等作业。如以“数学+3D 建模+泥塑创作”为核心的实践课程,就是通过数学分析中国建筑的对称美,分解对称美中蕴含的数字信息,引导学生通过观察、设计、带入、思考、操作等多种形式,尝试通过信息技术进行3D 建模,在建模过程中,思考三维空间里对称美的呈现形式,形成可供泥塑创作的3D 示范图。最后,通过3D 建模过程中形成的空间对称美体验,创作体验数学对称美的泥塑作品,进而培养学生在现实环境中解决真实的数学问题的能力,开展真实的数学学习,发展数学核心素养。
4. 模块四:数学的周期表达,体验数学的周期美
课程内容包括发现中国传统文化中的十二生肖、二十四节气以及音乐作品的周期表现(见表4)。
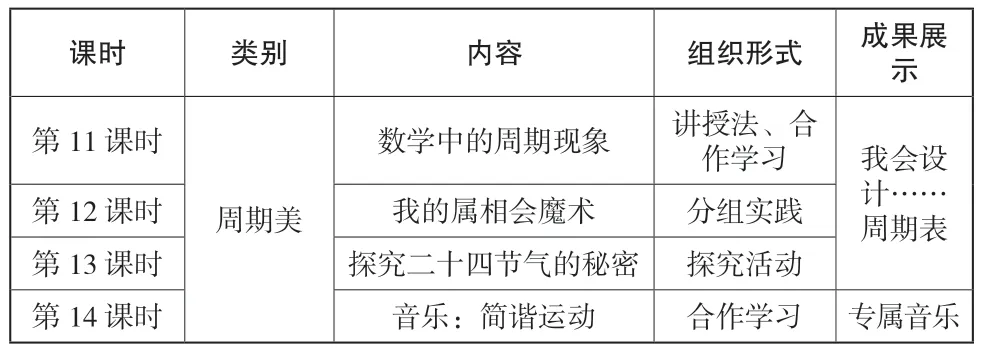
表4 数学的周期美
跨学科整合设计理念:以探究体验为活动主旨,融合数学、语文、科学、音乐、信息、劳动等学科,带领学生学习数学中的周期现象,引导学生通过十二生肖、二十四节气的变化了解周期现象,进而设计自己的周期表;借助音叉、单摆、弹簧等物体的振动特点,体会相同的时间间隔周期性地重复,设计出自己的专属音乐。
如音乐学科中音叉、单摆、弹簧这一类物体的振动有共同的特点,就是在相同的时间间隔周期性地重复,这类振动被称为简谐运动。毕达哥拉斯学派发现可以把音乐归结为自然数的比例关系:两个绷得一样紧的弦,如果一根是另一根长的二倍,会产生和谐的声音,相差八度;弦长的比为3∶2,会产生另一种和谐的声音,相差五度。得到一般的结论:音乐的和谐在于多根弦的长度成整数比,从而形成音阶。《管子》记载的“三分损益”要比毕达哥拉斯更早一些。“三分损益”包含“三分损一”“三分益一”两层含义。“三分损一”将长度a 三等分然后减去一份,得到a 的三分之二;“三分益一”将长度a 三等分然后增添一份,得到a 的四分之三。方法交替、连续运用,得到长度比例为2 ∶3 ∶4,得到和谐的声音。古代中国五声音阶,分别命名为宫、商、角、徵、羽,相当于现在音阶的1、2、3、5、6,因此这样的方法也被称为“五度相生律”。这样跨学科主题课程的学习,既发展了学生艺术素养,也增强了学生的民族自豪感。
5. 模块五:自然的和谐,体验数学的和谐美
课程内容包括黄金比的认识,剪纸、印章与绘画创作以及自然界和谐美的发现(见表5)。

表5 数学的和谐美
跨学科整合设计理念:以创作活动为思路,融合数学、科学、美术、信息、劳动等学科,先带领学生学习数学中的黄金比,渗透和谐美,引导学生创作剪纸作品、刻制印章或绘画,体会数学的和谐美在艺术中的表现;引导学生发现龙舌兰叶片的生长顺序、向日葵果实的排列等现象,发现自然界的和谐美。
四、课程评价
以表现性评价为主,以星级方式公示并记录,表现性评价由过程性评价(80%)和总结性评价(20%)两部分组成。最终成绩=模块一成绩(20%)+模块二成绩(20%)+模块三成绩(20%)+模块四成绩(20%)+模块五成绩(20%)+总结性评价成绩(20%)。
模块一成绩由学生互评产生,模块二、 模块三、模块四的成绩由学生自评产生,模块五的成绩由教师评价产生,过程性评价结果和总结性评价结果累计作为课程最终成绩。依据星级颗数,总分在90—100 颗星为优秀,75—89 颗星为良好,60—75 颗星为合格。
评价依据:数学知识掌握、跨学科学习表现、模块学习成果。总结性评价关注下列要点。
(1)数学知识评价要点:能够从生活中发现数学美,能够运用数学语言表达生活中的美,能够运用数学评价生活中的美。
(2)模块作品评价要点:作品完整且体现跨学科学习的成果,内容形象,形式丰富,设计巧妙,比例协调,富有想象力和创造力。
1. 模块一(20 颗星)
结合同伴的表现,选择最适合他(她)表现的星级,表现等级为5 星、4 星、3 星,共三档(见表6)。
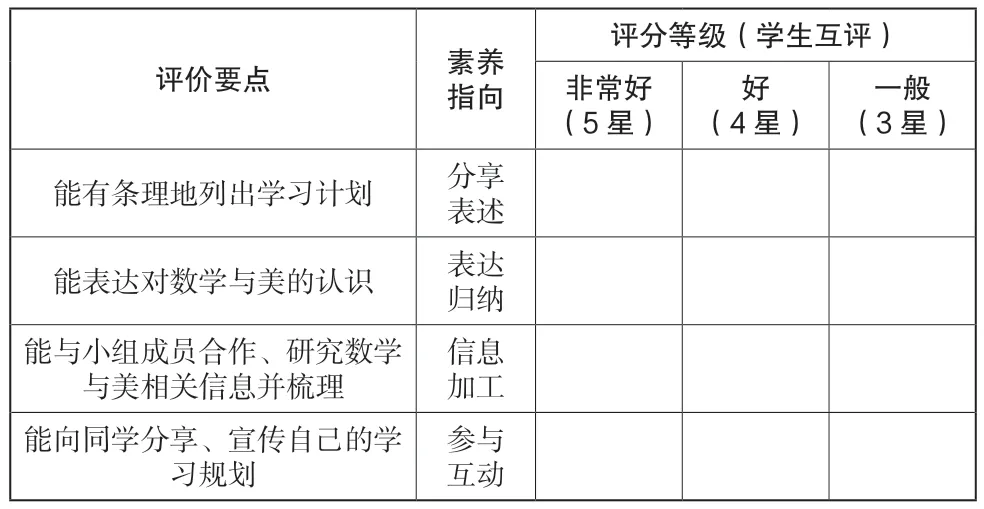
表6 《学习规划手抄报》评价
2. 模块二(20 颗星)
结合自己的表现,选择最适合自己表现的星级,表现等级为5 星、4 星、3 星,共三档。
评价要点:能整理了解与数学有关的古诗词;能根据数学知识恰当选择合适的诗词;能和组员一起参加诗词大赛;能和同学、家人分享作品。
素养指向:信息归纳;实践表现;合作探究;分享表述。
3. 模块三(20 颗星)
结合自己的表现,选择最适合自己表现的星级,表现等级为5 星、4 星、3 星,共三档。
评价要点:能向小伙伴介绍自己的作品造型;能运用数学知识美化自己的作品;能与人合作创作符合对称美的作品;能大胆地向大家介绍自己的作品。
素养指向:信息归纳;实践表现;合作探究;分享表述。
4. 模块四(20 颗星)
结合自己的表现,选择最适合自己表现的星级,表现等级为5 星、4 星、3 星,共三档。
评价要点:能创作……周期表;作品能够体现数学的周期美;能与人合作,共同完成音乐创作任务;能依据创作的……作品创编故事。
素养指向:创作表现;创新表现;合作表现;表述创新。
5. 模块五(20 颗星)
教师结合学生的表现,选择最适合学生表现的星级,表现等级为5 星、4 星、3 星,共三档。
评价要点:能创作剪纸或印章或绘画作品;作品能够体现数学的和谐美;能与人合作,共同完成微视频的拍摄任务;能依据创作的微视频创编故事。
素养指向:创作表现;创新表现;合作表现;表述创新。
五、结语
数学与美之间具有充分的联系,这种联系有一些是显性的,容易发现;还有一些是隐性的,需要进行更深入的挖掘。通过实践得出如下结论:
(1)数学与美课程设计与实践符合数学课程改革发展的方向。
(2)数学与美课程设计与实践具有可行性和可操作性。
(3)教师应结合教材和其他学科开发课程资源,并在教学中实践。
在学生的视野中有两个世界,一个是分学科的知识世界,一个是缤纷的生活世界。教师要教会学生将知识世界中的科学知识整合应用于生活世界,这是教育的本质,也是此次课程改革提出的新的价值取向。数学与美的跨学科主题学习课程是数学课程整合领域的一个新尝试,具有趣味性和创新性,深受学生们的欢迎。
数学与美的跨学科主题学习课程从不同的侧面反映了人类对自然界的认识,反映了人类的想象力和创造力,表达了人类的情感。数学与美跨学科主题学习课程的最终目的,不是使学生能够说出数学与美到底有哪些关联,而是达到一种潜移默化的效果和发展学生核心素养的目标。
