小学教育：追求一种真实的存在——以人教版数学教材二年级下册为例

范午英 华应龙

（1. 邢台市金华实验小学，河北 邢台 054099；2. 北京第二实验小学 北京 100045）

上课是有多重境界的。

20 年前的我，只是把上课看作一份工作，虽然人在讲台上，但没有沉浸其中，印象里只有固定的课本、无尽的习题和令人忐忑的平均分，其他什么也没留下。现在的我已过不惑之年，终于感悟到了上课的又一重境界：当我把自己对数学的理解表达出来时，学生的反应往往出乎意料，于是双方都享受着思维火花碰撞的快感，虽然它“迎之不见其首，随之不见其后”，但我们总相信下次邂逅一定在不久后的某节课上。

一、真实的统计更有意义

（一）缺勤也想起作用

第一单元《数据收集整理》，例2 是这样的：学校要举办讲故事大赛，某班要从两位同学中选一位参加，经过大家投票，王明明得15 票，陈小菲得22 票。① 根据统计结果，应该选陈小菲参加比赛。② 有两位同学缺勤没能参加投票，如果他们也投了票，结果可能会怎样？因为两位候选人相差7 票，所以两个缺勤的同学即便都投给王明明，也起不了什么作用，不能改变结果。

我的问题来了！

师：如果班里投出怎样的结果，缺勤的两票就能起作用？

生1：王明明21 票，陈小菲22 票。

师：你注意到了两人的差距要小，这很好。但忽略了一个问题。

生2：目前的总票数是37 票，代表37 个同学，这是不能变的。所以两人的总票数应该是37 票才对。

生3：王明明18 票，陈小菲19 票。如果最后两票一人一票，那么陈小菲参赛；如果最后两票都投给陈小菲，也是陈小菲参赛；如果最后两票都投给王明明，王明明参赛。

师：最后这种情况，剧情反转了，这两票终于起到了决定性的作用。

生4：也可以王明明19 票，陈小菲18 票。

师：两个人只能相差1 票吗？能不能票数相等？或者相差2 票？

生5：票数相等做不到。因为37 是个单数，不能正好平均分成两份。

生6：你看现在差1 票（指着18 比19 的情况），如果投给王明明的1 票变成投给陈小菲的，就变成17比20 了，两人会差3 票，但不会差2 票。变成17 比20 以后，最后两票又不起作用了。（这里运用“比”的说法，只是类似于体育比赛中的比分而已）

师：看来要想最后两票发挥作用，两人在班里的投票结果只能是相差1 票。

原来统计与运算的结合，不只是比多比少、求和之类的常见手法，根据数据特点和隐含条件还有很多文章可做。

（二） “其他”应付不过去

练习一的第6 题（如图1）旨在让学生经历数据的收集和整理过程。

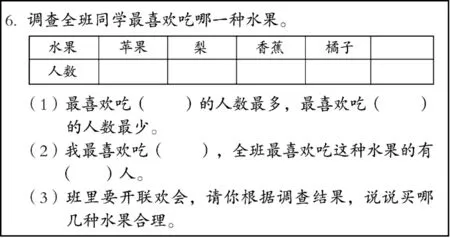
图1 练习一第6 题

每个同学先把第（2）题第一个空填好：我最喜欢吃什么？然后逐一汇报，请5 位同学在黑板上画“正”字统计。统计完毕，选苹果的2 人，选梨的5人，选香蕉的4 人，选橘子的10 人，选其他的33 人（喜欢其他水果的都归于此）。核对总人数是54 人，没有问题。

但填空时发现第（1）题不好填了：最喜欢吃（其他）的人数最多。这是个什么结论！以后就买“其他”这种水果吗？看来“其他”是应付不过去的，里面还藏着不少秘密。一不做二不休，再把这33 个人统计一遍，又出来了9 种水果（见表1）。一个有意思的细节是：开始有人报“樱桃”，后来又有人报“车厘子”，我正要写成两类，学生喊道：“车厘子就是樱桃。”我真不知道！网上一查，原来国外的大樱桃叫车厘子，我又长知识了！

表1 统计表格

我让大家把表格延长到了课本的右边一页，一共有13 种水果。喜欢吃橘子的人数最多，喜欢吃菠萝和蓝莓的人数最少（还出现了并列）。如果运用这一调查结果的话，应该是橘子、西瓜和桃子多买一些，其他的水果各买一点（并不是一点不买）。

教材编者大概以为前面列举的4 种常见水果一定占大多数，没想到如今富足的生活已今非昔比，喜欢的水果相当多元了。这件事也是可遇不可求的，假如课堂上没有出现“其他”最多，也就没有后面的精彩了。

二、真实的运动更有联系

（一）简单变得不简单

第三单元是《图形的运动（一）》，练习七第14题是一道很简单的选择题（见图2），只有（3）是由（1）平移而来。如果仅仅到此，未免可惜了这么大的版面。

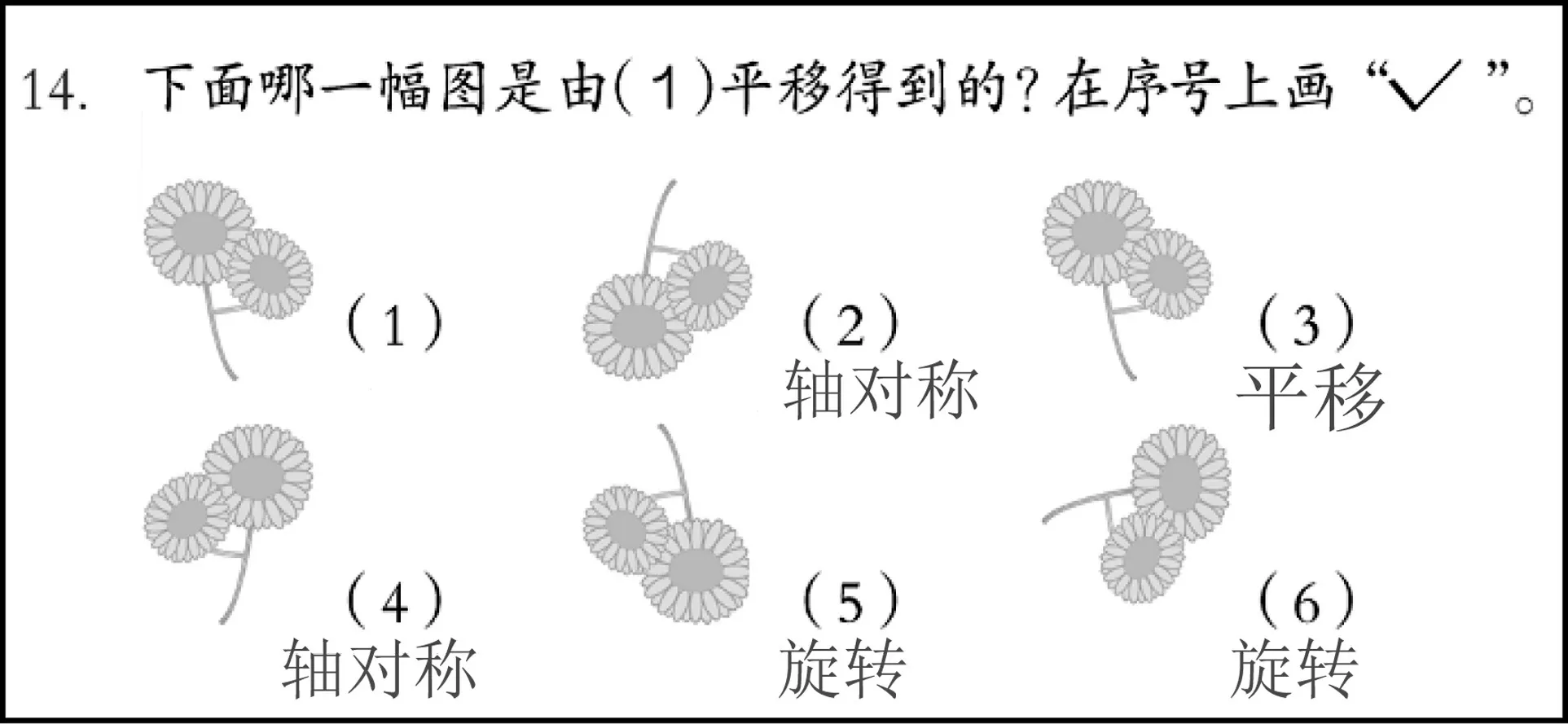
图2 练习七第14 题

师：其他几幅图又是（1）经过怎样的运动得到的呢？”

生 1：（5）是由（1）旋转而来。

生2：（6）也是由（1）旋转而来的。

师：如果（1）是顺时针（可以教，学生听得懂）旋转的，先转成哪个图？”

生3：先转成（6），再转成（5）。（把书旋转起来，再和大屏幕对照验证）

师：（2）和（4）呢？（平移、旋转都做不到了，学生们开始沉思）

王熙：我想用轴对称试一试。

师：哪里是对称轴呢？

王熙选择在（1）的左边竖着画对称轴，等把左边一半补充完整，竟然和（4）一模一样！

王熙：（4）是由（1）经过轴对称的方法得到的。

师：非常好！如果把（1）看作一个小印章的话，通过“合书”的动作，就可以得到（4）。

师：最后剩下（2），又该怎么得到？

生4：由（4）旋转可以得到。

生5：由（5）利用轴对称可以得到。

师：也就是说从（1）到（2）要经过两步，比如“轴对称＋旋转”，从（1）到（4）再到（2），或“旋转＋轴对称”，从（1）到（5）再到（2）。

突然，关怡然高高举起手，迫不及待地说：“利用（1）的轴对称可以直接得到（2）！”

师：对称轴在哪里？

关怡然：（1）下面，横着！

王熙的想法我在备课时想到了（对称轴在右边也可以），这里确实有超范围之嫌，但如果把已知图形看成轴对称图形的一半就讲得通了，正好可以发展学生想象力。针对从（1）到（2），我开始以为必须用两步，而关怡然的思路突破了我的思考范围，原来对称轴的位置变化就可以代替旋转。

妙哉！出乎了我的想象。

（二）小小乌龟又建功

刚刚尝到甜头的我，面对一切机会，都如法炮制。练习七的第4 题（见图3），有3 条小鱼可以通过平移与红色小鱼重合，另有2 条可以通过旋转达到目标（根据题目情景，严格地说旋转以后还需要平移），最后的重点落到了离红色小鱼最近的那条鱼上。

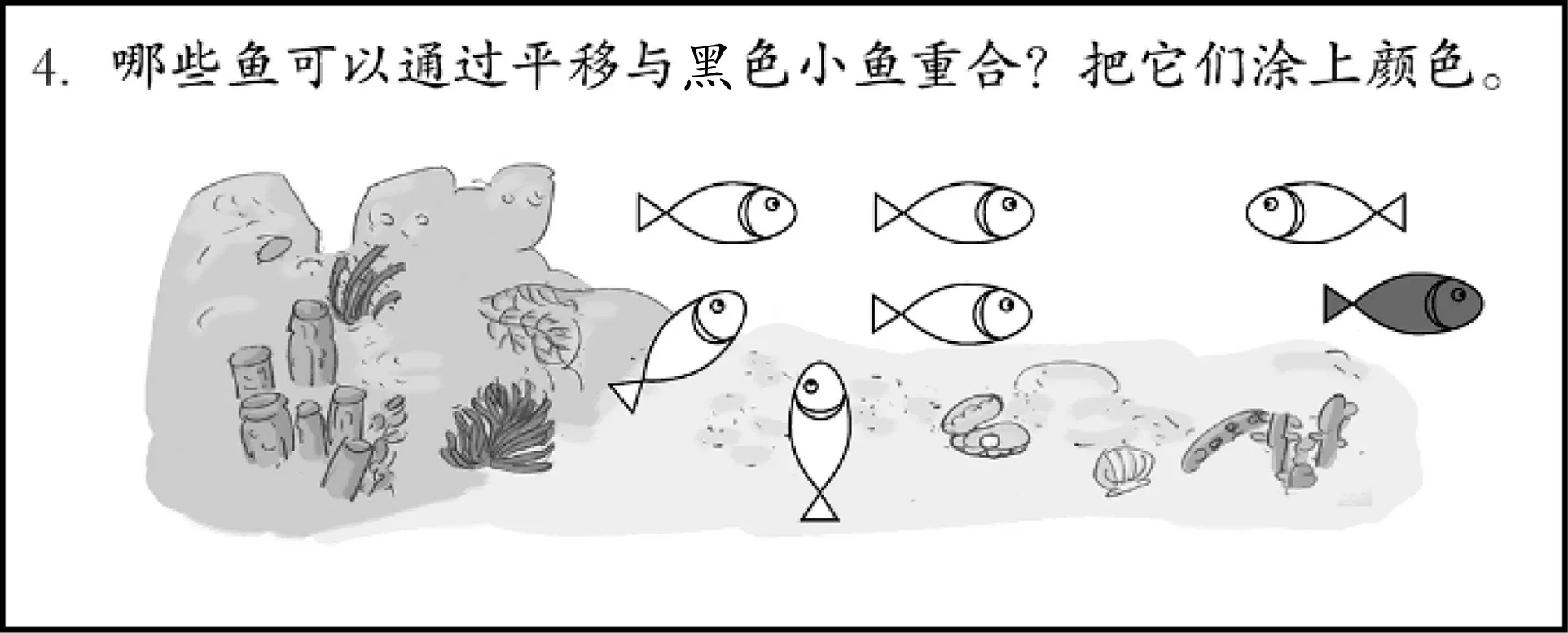
图3 练习七第4 题

生1：通过轴对称可以得到。

生2：通过旋转也可以得到。

师：这道题和昨天讲的“两朵小黄花”的题目还是有些不同的，需要再平移一下。

接下来第5 题的焦点是乌龟（见图4）。

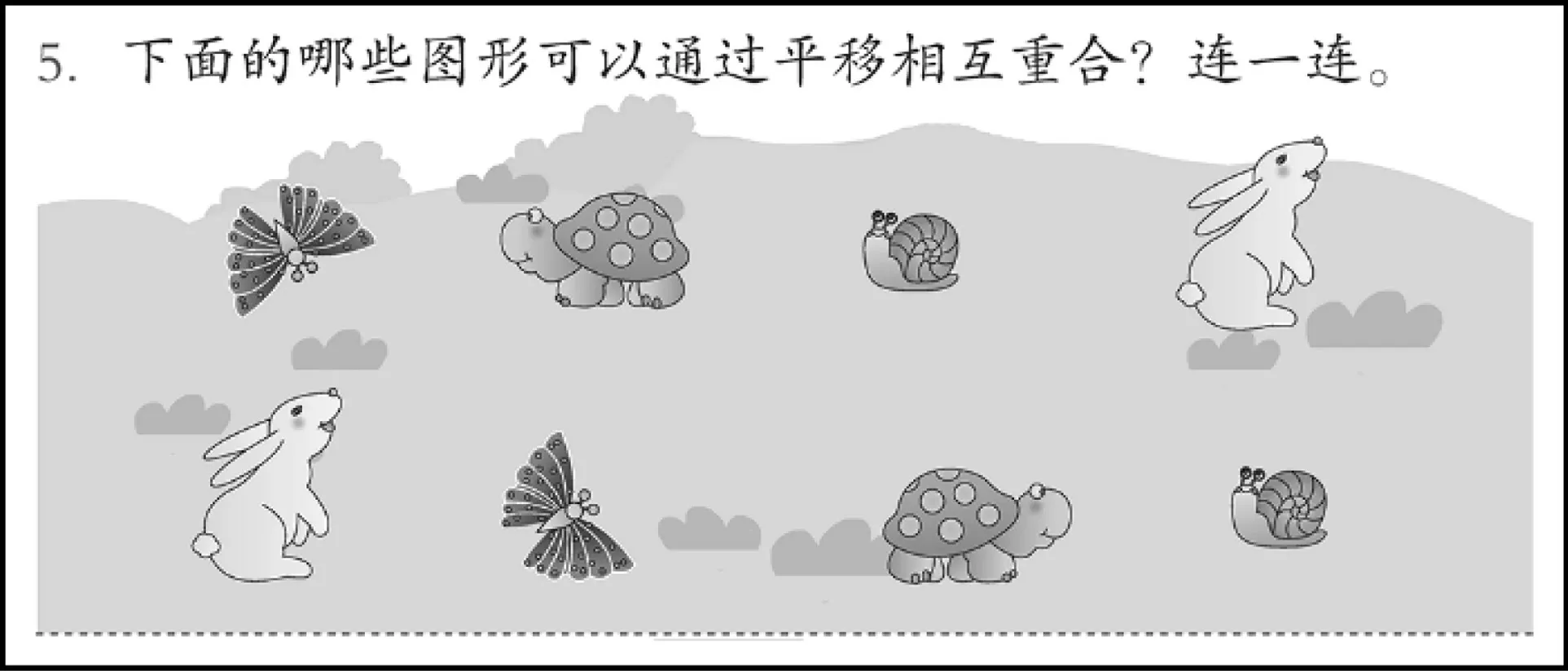
图4 练习七第5 题

生3：乌龟不能通过旋转得到。因为旋转以后，龟壳朝下，四脚朝天了。

我突然警觉起来，重新返回第4 题。

师：为什么小鱼既可以轴对称，又可以旋转，而乌龟就不行呢？

生4：因为小鱼上下一样。

生5：如果小鱼的背上还有些标记（比如鱼鳍），就不行了。

师：也就是说，实际上通过旋转，小鱼也是背部朝下，只不过由于上下相同，看不出来罢了。

生6：注意看鱼的眼睛！眼睛是偏上的。如果旋转的话，就应该偏下了。所以这条小鱼根本就不能通过旋转和小红鱼重合。

实话实说，这个地方的课我没有备好。所幸碰到了可爱的乌龟，补救了我在小鱼身上的过失。这一失误犹如飘飘然间泼来的一盆冷水，浇醒了我——什么时候也不能想当然啊！数学崇尚联系，但不能丢失了严谨。看来对于前文发现的“轴对称”运动的妙用，还没有彻底理解：对称轴的位置变化可以省略旋转，但旋转却不能代替轴对称，两者本质不同——旋转是绕中心转动，所有的方向都在变化；而轴对称是以轴为分界，垂直于轴的方向相反，平行于轴的方向不变。

三、真实的计算更有深度

（一）露出久违的笑容

对于低年级小学生来说，口算是打基础的。我以为“六表”必须背熟（“六表”指10 以内加法表、10以内减法表、20 以内进位加法表、20 以内退位减法表、乘法口诀表和本册第45 页的除法表）。为此我是不遗余力的，班上每位同学都逐一计时过关。两年来，花在这件事上的时间占到了课下辅导的一半。每次背诵前我都做示范，我所用时间的3 倍一般为要求学生背诵的时间。即便如此，仍然有6 个“老大难”被剩了下来。我耐心地等了好几个月，还是没有多大效果。这时我意识到应该改革练习形式了。

游戏一：6 个人开火车，轮到谁了，背不出了就站着，等下一轮又轮到你，背出来了再坐下。

游戏二：找来一个大书包，像击鼓传花似的，如果背不出来拿书包的时间就长一些，直到背出来为止。

我让他们几个人自己玩这些游戏，我远远地做其他事情。没想到他们还创造出了新规则，比如背不出来的要“提书包5 次”，以示惩罚。更可喜的是，他们说话的声音也大了，每个人的脸上都露出了久违的笑容。我把记录这些活动的教学反思发给相关学生家长，于是家里面也热闹起来。

紧接着，我又想到一个方法——边换数边背表（其实并不是死记硬背，只不过是想得快一些罢了）。因为这些四则运算表格是有规律排列的，每次通常只是改动一个位置的数。比如除法表竖着看，第4列是（ ）÷4 ＝□，除数不变，商从小到大依次排列。这时只需要想被除数即可（本来除法表就是乘法口诀表的另一种训练形式），即每次擦除更换一个商，然后想被除数是谁。这个活动很适合在黑板前使用黑板擦，比在练习本上用橡皮擦还方便。大家一人一组，轮流练习，很受欢迎。

游戏的作用很快显现出来，两周内就有4 名同学完成了久拖不决的全部任务！剩下的2 个人，也都完成了一半。我还要继续等下去，直到他们成功上岸。

俗话说艺不压身。低年级口算基础打得牢，以后做笔算、估算、简便计算都不费劲，也能腾出时间来思考分析其他问题。当然也没必要夸大游戏的价值，如果没有前面反复记忆的基础，单靠游戏也恐难奏效。

（二）我的最爱——算式谜

巧解算式谜很有趣，尤其是多位数乘除法算式谜，更是变化多端。我专门总结了算式谜的特征——千疮百孔，能够复原。面对二年级的有余数除法，我也想引入算式谜。虽然这是学生第一次学习笔算，但有余数除法已经具备了算式谜的基本特征。

首先是完成两道常规题目，然后思考：哪个位置上的数擦掉后，还能通过推理恢复原数？为什么能复原？这里主要依靠两种关系：商×除数＝分下去的积；被除数－分下去的积＝余数。竖式中被擦掉的数越来越多，最终7 个位置剩下了3 个。当然不能只把被除数和除数剩下，那是顺向计算，而非算式谜。

我在课上重点介绍了一种搜索乘法口诀的新方式——按积的个位搜索。其中1、3、7、9 的乘法口诀，它们口诀积的个位正好是从1 到9，不多不少，也就是说已知积的个位就完全确定了是这组口诀中的哪一句；而2、4、6、8 的乘法口诀，口诀积的个位则是2、4、6、8、0，其中积的个位是2、4、6、8的，都是两种答案，需要认真甄别；最特殊的是5 的乘法口诀，口诀积的个位只有5 和0。

比如左边一题（见图5），7 的乘法口诀中，积的个位是3 的只有七九六十三，从而确定商是9，分下去的积是63，被除数是69。右边一题，4 的乘法口诀中，积的个位是2 的有两种情况，三四十二、四八三十二。所以除数可以是3，也可以是8，但因为余数是3，除数必须比余数大，所以除数3 被淘汰，只能填8，分下去的积是32，被除数是35。

图5 算式谜

循着老师编题的过程，同学们课下自己编题，每人4 道。我从中挑选了30 道最优秀的，大家一起做。挑选标准是答案唯一、构思巧妙、类型丰富。每一种都缀有学生的名字，大家还真是动脑筋了。

通过编题活动，我对算式谜也有了新的理解。第一，余数对除数有反制作用。即除数必须比余数大，可以利用余数的大小控制除数的可能性，使答案变得唯一，但是余数不能制约商。第二，有时单凭积的十位或个位也可以找出线索。第三，空格的位置也会说话，所以一般的算式谜都是“七露三”，但也有些“七露二”的，甚至是“露一”的绝版。

四、真实的认数更有趣味

（一）捆住一千根小棒

第七单元《万以内数的认识》是对认数范围的一次扩展。表面上看只是增加了千位和万位这两个数位，但实际上是在原来100 个数的基础上增加了9900 个数。这么多的数突然来到面前，可以说是喷涌而出，学生自然应接不暇，出现的问题很多。我想应该做好两件事，一是对计数单位的直观认识，二是对十进位值制的深入理解。

课本上认识“一千”使用的是小正方体，其中也有体积的渗透，但操作不方便，必须使用多媒体课件。而课件毕竟是抽象的，演示的速度很快，缺少了过程的价值，也没有实物带给学生的冲击力。最终我选择了双头棉签上的小棒。要求每位同学带30 根，每10 根捆一小捆。而我则拿来女儿用的小皮筋，还有一根捆青菜的塑料绳。

上课伊始，先数好10 个十，用一根皮筋捆起来，成为一个中捆，这样10 个十就看成了1 个百。继续边拿边数，从110 数到200，再捆出一个中捆，又出现一个百，一共是两百了。接着从210 数到300，再捆出一个中捆……就这样一边收小棒，一边十个十个地数，一直数到960，全班所有小捆的小棒都用完了（班上总有学生只拿小棒但不捆起来的，所以我才把“每人带2 小捆”调整为“每人带3 小捆”）。这时有些学生手里还有单根的，正好可以拿来一根一根地数，又从960 数到了1000。面对来之不易的10 个“百”，我拿出塑料绳认真地捆起来，就是想给学生一个深刻印象，强调10 个百是一千。

虽然讲1000 以内数的认识，但不能局限于此。只要有小棒就可以接着数。就这样一直数到1249 根。我把这些小棒用胶带贴到教室里（见图6），这样的直观刺激，展示一星期，回味好几年。

图6 计数小棒

在认识一千的过程中，我带领同学们经历了10次十位的“满十进一”、1 次百位的“满十进一”，这些有意放慢的瞬间使他们记忆牢固。而最后那一千根的大捆更是让大家惊奇。一下课，就有很多同学围过来又看又摸。宋怡然说：“我还从没见过这么多小棒在一起呢！”

（二）关于敲门的故事

虽然学生有学习两位数的基础，但数四位数还是很难的，数到拐弯的地方容易迷糊，而且这时的弯拐的还有大有小，更易混淆。我的想法是：观察数数中的变与不变，只要掌握了这个规律，基于十进位值制的数数就会变得简单。

课堂上我从6772 开始数数（因为正好学到南京长江大桥的铁路桥长6772 米），并把数数的过程编成了故事。

个位、十位、百位、千位是兄弟四人，他们住在并排的四间房里，平时主要的工作就是一起表示一串串数。住在右边的个位最勤劳，每次数数他都变，但越往左，房间里的人越懒。

有一次，他们接到一个任务，要从6772 开始数数。于是个位开始忙碌起来……直到变成6779 后，个位去敲十位的门。个位说：“注意啦，十位醒醒，我这马上就满十了，要向你进一，准备开门吧。”

到6789 时也是如此。但到6799 时，不仅个位敲了十位的门，十位也紧接着去敲了百位的门，因为十位也即将攒够10 个十，也要“满十进一”了。接下来就变成了6800。

然后，百位继续睡大觉，十位又变成每隔10 个数醒一回，一直到了6900，后来又到了6999。这时候更热闹：个位敲完十位的门，十位就去敲百位的门，最后百位又去敲了千位的门，总共要敲三次！因为下一个数是7000！

等到数过7000 之后，千位沉睡，百位熟睡，十位打盹，勤劳的个位继续每次都变化……

故事中的“逢9 敲门”，预示即将“满十进一”。拐小弯敲一次门，拐大弯就要敲2 次门，甚至3 次门。数数的这种左慢右快的特点像极了钟表上的时针、分针和秒针（但时间不是“满十进一”）。实际上，也不能怪左边懒，而是因为规则所限。假如左边的高位数字一直变的话，右边的低位数字早就转晕了。

我以为，这些真实的片段就是小学教育里应该有的样子。这种状态大概就是“福流”。我深知万万不可满足于此，要继续向着教育的更高境界出发，一路汇集更多的探寻者。