一种具有学习机制的海鸥优化算法
2022-10-06王培崇尹欣洁李丽荣
王培崇, 尹欣洁, 李丽荣
(1.河北地质大学 信息工程学院,河北 石家庄 050031;2.河北地质大学 人工智能与机器学习研究室,河北 石家庄 050031;3.河北地质大学 艺术学院,河北 石家庄 050031)
0 引言
近些年,元启发算法[1]发展迅速,2019年的海鸥优化算法(seagull optimization algorithm,SOA)[2]就是元启发算法的代表算法之一。该算法通过模拟海鸥种群的协作飞行和捕食猎物实现对问题的求解,并在多个工程领域内得到了成功应用。但是,由于该算法缺少严格的数学理论支持,在解决较高维度的函数优化问题时出现了收敛速度慢、解精度低和容易早熟等问题[3-5]。
针对标准SOA容易早熟、解精度低等问题,毛清华等[6]提出一种融合改进Logistics混沌和正弦、余弦算子的自适应t分布海鸥算法,该算法采用改进的Logistics混沌映射机制初始化种群,在种群的搜索阶段引入正弦、余弦算子更新个体的位置,并引入非线性收敛因子协调算法的局部搜索和全局搜索,加快算法的收敛速度;同时,为了克服算法早熟,对种群内最优个体所在的位置引入自适应t分布变异策略加以扰动。王宁等[7]提出一种黄金正弦引导与Sigmoid连续化的海鸥优化算法,该算法在海鸥迁徙阶段,引入Sigmoid函数的惯性权重引导海鸥种群的全局搜索;在捕食阶段,将置信度低的区域设置为搜索禁忌,保证种群一直向置信度高的优秀解空间区域飞行;并且加入黄金正弦机制帮助种群寻找搜索范围,指引种群的位置更新,提高寻优能力。秦维娜等[8]提出一种基于惯性权重的海鸥优化算法,采用非线性递减的惯性权重计算附加变量的值来调整海鸥的位置,通过Levy飞行和随机指数值增加海鸥飞行的随机性,增强算法搜索寻优的全局能力,避免算法寻优搜索陷入局部最优。Che等[9]提出了一种混合鲸鱼-海鸥优化算法,该算法首先在SOA螺旋式攻击行为中融入鲸鱼优化算法的空间收缩策略,以提高SOA的计算精度;其次,在SOA的搜索算子中引入Levy飞行策略,引导算法跳出局部最优的约束。上述改进机制在一定程度上改善了算法的性能,但是均没有考虑种群内粒子之间的信息交流问题。
本文提出一种具有学习机制的改进海鸥优化算法(improved SOA with learning,ISOAL)。该算法在迁移算子中引入基于当前粒子和种群均值间差异的学习机制,在算法的后期引入精英粒子的反向学习(opposition-based learning,OBL)[10-11],以提升算法性能。
1 标准海鸥优化算法
标准海鸥优化算法流程如图1所示。
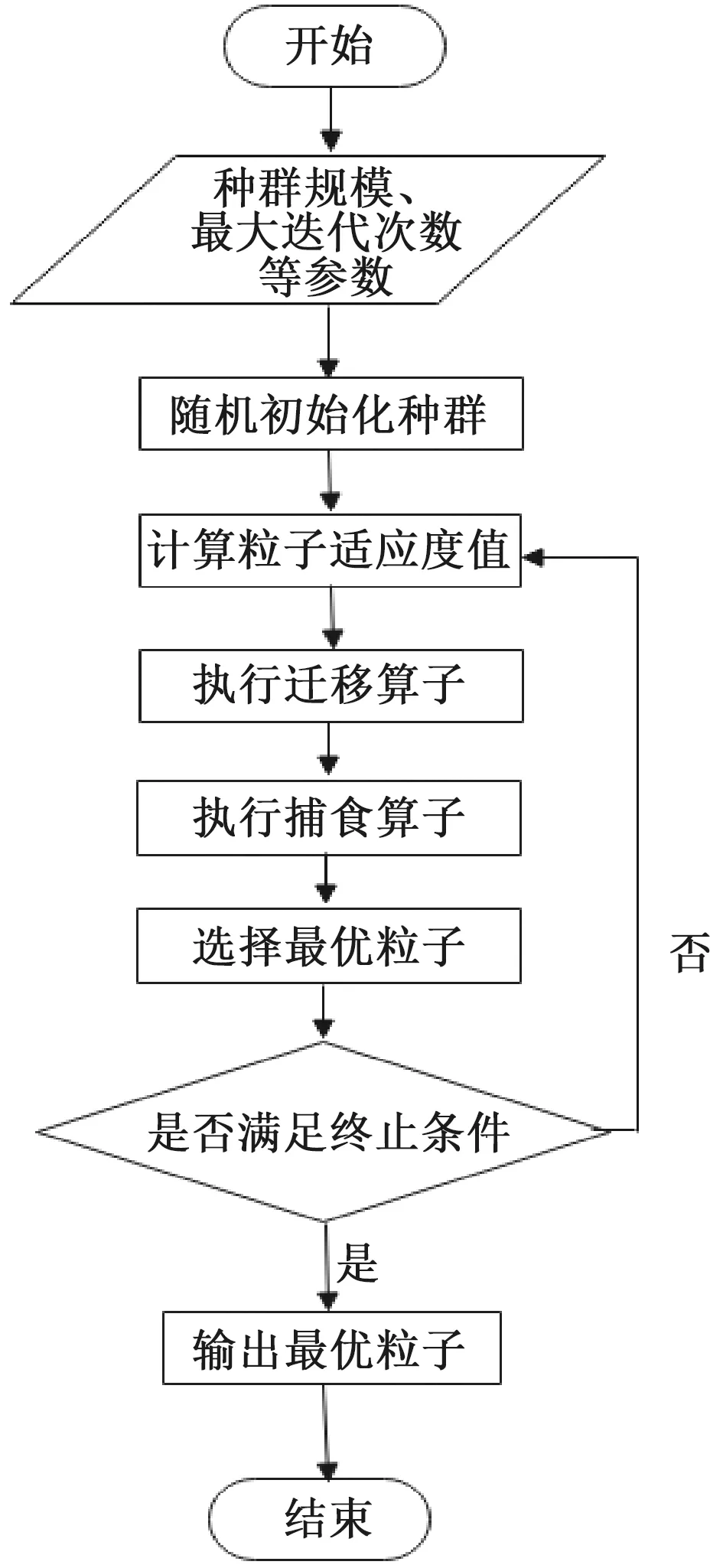
图1 标准海鸥优化算法流程Figure 1 Flow chart of standard SOA
1.1 迁移算子
(1)
(2)
式中:A=fs-[t·(fs/Tmax)],fs=2,Tmax为最大迭代次数;B=2A2·rand(0,1)。
当前粒子与最优粒子之间的相对距离为
(3)
1.2 捕食算子
海鸥采用一种螺旋式飞行的方式对猎物进行攻击,在三维空间的运动为
(4)
式中:r为海鸥在螺旋飞行时的半径;θ∈[0,2π]为随机角度;u、v为常数。
当前粒子的捕食算子为
Xi(t+1)=Di(t)·gxgygz+Xb(t)。
(5)
综上,算法迭代过程中的当前粒子轨迹为
Xi(t+1)=|(A-B)·Xi(t)+B·Xb(t)|·
gxgygz+Xb(t)。
(6)
2 具有学习机制的海鸥优化算法
由式(6)可知,海鸥优化算法的迭代过程仅有2个参数。其中参数A为线性变化,在一定程度上提升了算法的收敛速度,但对于解空间为多峰的复杂优化问题,算法容易忽略部分解空间。此外,该算法没有考虑种群内部非最优粒子之间的信息交流和互动行为,而自然界中的生命群体均会存在内部信息的沟通和学习行为,这种学习行为在很大程度上可以主导种群的演化方向。基于此,本文将从以下几个方面对算法进行改进。
2.1 基于学习机制的迁移算子
记Xm(t)为当前种群全部粒子的平均状态值,则式(1)的空间搜索机制更新为
(7)
式中:α为(0,1)的随机数;Xm(t)-Xi(t)表示当前粒子向种群均值学习,这样可以在算法早期有效扩大搜索范围,避免过早的收敛。
2.2 参数A的改进
标准SOA中的参数A受fs的制约,从2线性递减到0,收敛速度较快。但是,大多数优化问题的解空间为非线性,线性参数并不适合对空间进行有效搜索,容易忽略部分空间。因此将参数A调整为非线性以保证粒子对解空间的非线性搜索,见式(8):
(8)
式中:betarand(·)为能产生beta分布的随机数生成器。
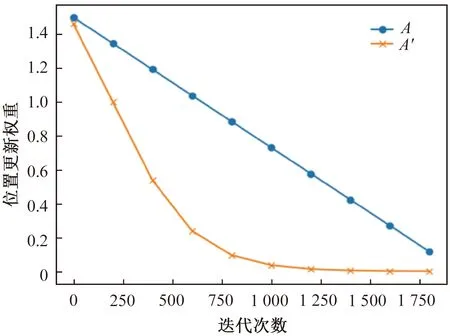
图2 参数A和A′随迭代次数的变化曲线Figure 2 Curves of A and A′ with the number of iterations
2.3 精英反向学习
群体智能算法中,适应度优的精英粒子必然包含了更多的引导种群向全局最优收敛的有益信息。令精英粒子执行反向学习,既能加快算法的收敛速度,也加强了算法的局部探索能力。
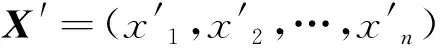
定义2基于反向解的优化。设待优化问题为最小问题,适应度函数为f(X),若存在某个可行解X,其反向解为X′,若f(X′) 算法1OBL算法。 输入:个体Xi(t),下限a,上限b,最大迭代次数Itermax; 输出:最优个体Xi(t); Step 1 设置迭代次数为m=0; “对对,就是那个乾隆皇帝的‘乾隆’,这‘乾隆通宝’,就是他在位时铸造的货币,不过因为款式面值,发行地各有不同,流传下来的‘乾隆通宝’也是各有差异。”老贾看向少的那一堆。孟导顺着老贾的目光看过去,果然发现那一小堆钱上正面基本都有“乾隆通宝”的铭文,不过反面朝上的则铭有许多自己不认识的符号。即使认真看了看,也分不出是哪国文字。 Step 2 生成一般化系数k∈[0,1],依据定义1生成反向解X′t(m),并保存; Step 3 迭代次数没有满足结束条件,则m=m+1,转至Step 2; Step 4 在Xi(t)和所产生的全部反向解中选择最优的个体替换Xi(t)并输出,算法结束。 算法2具有学习机制的海鸥优化算法ISOAL。 输入:种群规模N,最大迭代次数等参数; 输出:最优粒子Xb(t)。 Step 1 在解空间内随机初始化种群POP; Step 2 计算粒子的适应度值选择最优粒子Xb(t); Step 3 以式(7)、(8)替换式(1),执行迁移算子; Step 4 执行捕食算子; Step 5 精英粒子变化幅度小于0.01,则执行反向学习; Step 6 算法不满足终止条件,则转至Step 2; Step 7 输出最优粒子Xb(t),算法结束。 设算子最大迭代次数为Tmax,种群规模为N,分析上述算法可知,主要操作集中于Step 3~6,则时间复杂度为O(Tmax·N)。 为了验证所提算法的性能,应用MATLAB 2019编程实现上述算法,实验环境为联想笔记本(intel i7,16 GB)。选择10个CEC2017标准测试函数来测试算法的性能,列于表1中,以近年来最新算法HPSO-TS[12]、V-DVGA[13]、DADE[14]和CMA-ES[15]作为对比算法。ISOAL的种群规模设置为30,问题维度为50,算法的迭代次数为3 000。所有算法均独立运行30次,以消除偶然因素的影响,取解均值和方差进行对比,如表2所示。 表1 CEC2017测试函数Table 1 CEC2017 functions 表2列出了SOA、HPSO-TS、V-DVGA、DADE、CMA-ES与本文算法在CEC2017的10个函数上的解均值和方差。由表2可知,在单峰函数f1、f2、f3上,本文算法ISOAL的解均值和方差均最小。多峰函数f4、f6的解空间并不复杂,考验的是算法跳出局部最优约束的能力,从实验结果看,ISOAL在解均值和方差上比CMA-ES算法略差,但是仍然优于其他算法。多峰函数中的f5、f7、f8的解空间较复杂,存在多个局部最优极值点,因此,对应算法不仅需要有摆脱局部极值约束的能力,而且还要有一定的勘探新解的能力。在f5函数上,HPSO-TS、V-DVGA和ISOAL的解均值精度相差不大,ISOAL的方差优于其他几个算法,表现出较好的稳定性。在f7、f8函数上,ISOAL的解均值和方差均最小,稳定性良好。在函数f9上,ISOAL的解均值和方差均略高于DADE算法,但也在同一个数量级上,优于其他算法。函数f10是一个多峰函数且局部最优值数量众多,ISOAL同样表现出色,解均值和方差均最小,优于其他对比算法。 图3为V-DVGA、HPSO-TS、ISOAL和SOA算法在f1、f2、f3、f4、f5和f6上的收敛曲线。 图3 算法收敛曲线对比Figure 3 Comparison of algorithm convergence curve 由图3可知,在函数f1、f2、f3和f4上,ISOAL初始种群的最优适应度就已经优于其他算法,并且经过非常少的迭代次数就迅速收敛,收敛速度明显优于其他算法。在函数f1上,HPSO-TS搜索到的最小适应度值为0.224 5,ISOAL搜索到的最小适应度值为0.191 2,相比下降14.83%。在函数f3上,HPSO-TS搜索到的最小适应度值为0.165 7,ISOAL搜索到的最小适应度值为0.154 7,相比下降6.63%。在函数f5上,HPSO-TS与ISOAL搜索到的最小适应度值相差不大。在函数f6上,HPSO-TS搜索到的最小适应度值为0.363 3,ISOAL搜索到的最小适应度值为0.342 7,相比下降5.67%。在函数f2上,ISOAL算法和其他算法的收敛曲线在迭代初期交叉在一起,但是ISOAL算法在经过较少的迭代之后,能够迅速收敛到最优解周围,并开始进行勘探操作。结果表明,ISOAL所获得最终解的精度优于其他算法。 针对工程中常见的张力弹簧问题[16]进行测试实验,以检测本文算法在约束问题上的性能。实验目标是在满足挠度、剪应力和振动频率等约束条件下,获得最小质量的弹簧。其变量分别为弹簧的线圈直径W(x1)、弹簧的平均直径D(x2)、弹簧的有效线圈数L(x3)。该问题的目标函数(总代价)和约束函数分别为 (9) (10) 式中:0.05≤x1≤2.00; 0.25≤x2≤1.30; 2.0≤x3≤15.0。 表3列出了对比算法在该问题上的求解结果,对比算法的数据取自文献[16]。由表3可知,ISOAL在仅有8 000次的评价次数内,获得的总代价比SOA降低了3.5%,弹簧的线圈直径和平均直径分别下降了5.7%和3.5%。 表3 算法在张力弹簧问题上的结果对比Table 3 Result comparison of design of tension/compression springs 表4为对比算法约束条件函数值。上述实验结果表明,ISOAL能够比较好地解决约束优化问题,且具有良好的性能。 表4 弹簧设计问题的约束函数值对比Table 4 Comparison of constrained function values in design of tension/compression springs 为了解决标准SOA算法内部粒子之间缺少交流的问题,本文提出了一种具有学习机制的海鸥优化算法ISOAL。该算法引入了基于粒子状态差异的学习机制,使当前粒子先向种群内粒子的均值状态学习,再搜索非冲突位置,执行位置迁移,并将原参数A由线性递减修改为非线性自适应递减方式,增强种群对解空间的全局搜索能力。为了提升算法的解精度,在后期引入精英反向学习,通过该机制加强对精英个体所在空间的勘探。在CEC2017和张力弹簧上的测试实验表明,ISOAL不仅具有较快的收敛速度,还具有较好的解精度和鲁棒性。 海鸥优化算法出现时间较短,相应的研究成果较少,下一步应该加强对其收敛性能的研究。借鉴其他算法以改善SOA的性能,探索新的应用领域也是未来主要的研究方向。2.4 算法描述
3 实验及结果分析
3.1 无约束函数测试

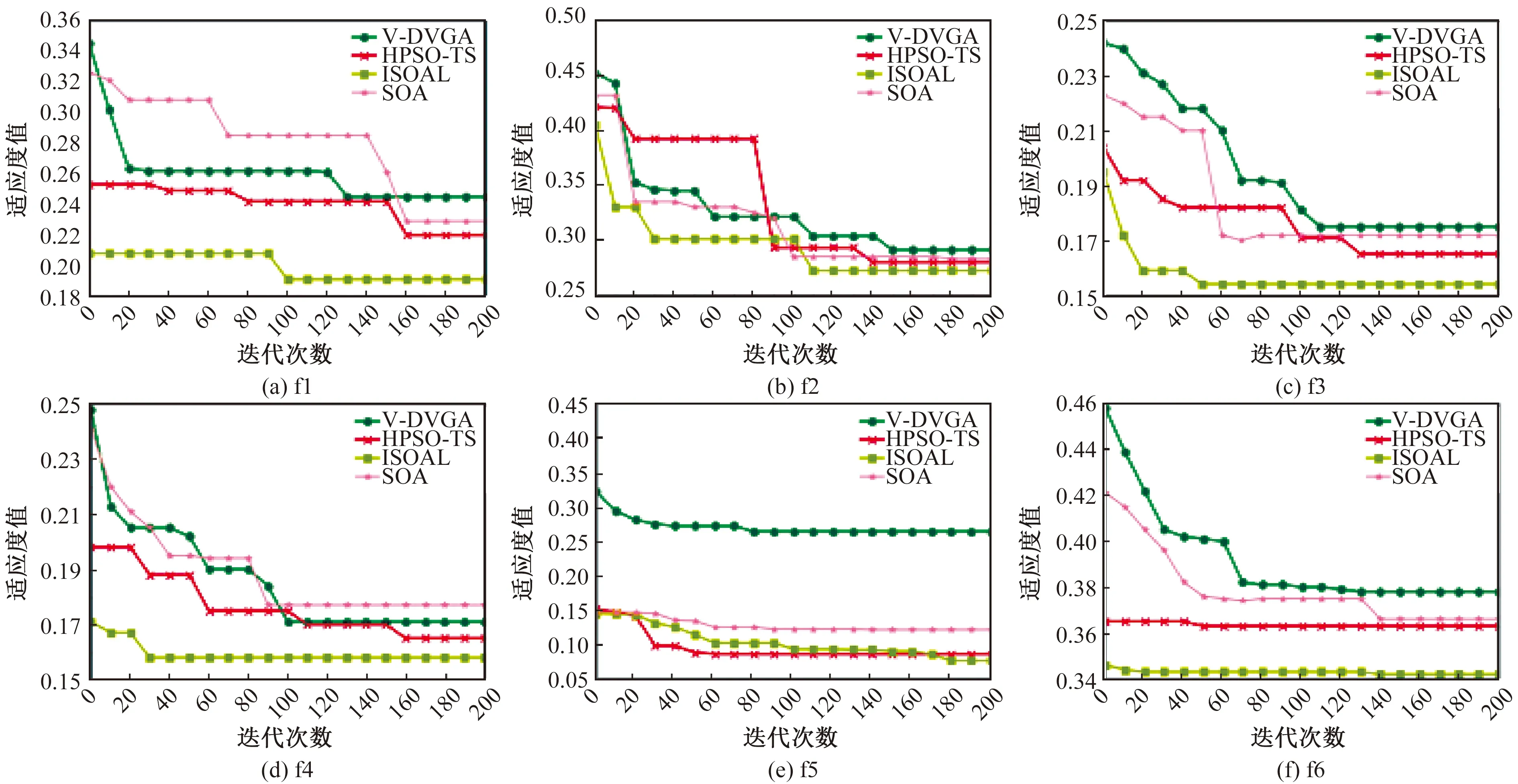
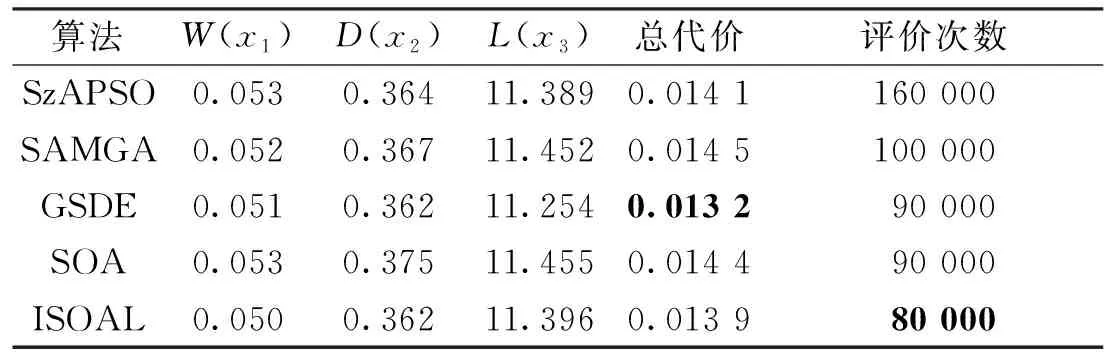
3.2 约束函数测试

4 结论
