基于差分和神经网络的同步辐射光源图像压缩方法*

符世园，汪 璐，程耀东,3，陈 刚

(1. 中国科学院高能物理研究所， 北京 100049； 2. 中国科学院大学， 北京 100049； 3. 四川天府新区宇宙线研究中心， 四川 成都 610213)

作为众多学科前沿领域不可或缺的大科学装置，同步辐射光源装置会产生海量数据。以正在建设中的北京高能同步辐射光源为例，一期工程预计平均每天产生200 TB的原始实验数据，峰值可达每天500 TB[1]，数据期望保存时长为半年，其中成像实验线站产生的图像数据量最大，所需存储和传输资源最多。实验样品被平行光照射后会得到一个投影图，每次成像之间会将样品在水平方向旋转一个很小的角度，最终得到该样品在不同角度的16 bit单通道灰度图像序列，该序列具有高分辨率、高帧率的特点。持续大幅增长的数据量和较长的原始数据保存期限给数据存储和传输带来很大挑战，图像压缩将是解决这一问题的主要方法。同时，为了充分挖掘原始数据中的科学潜力，图像压缩过程中最好没有信息损失。

目前通用无损图像压缩方法主要通过消除图像内部冗余进行压缩，但是无法消除图像序列中的时间冗余；视频压缩方法，比如通用的视频无损压缩和基于神经网络的视频压缩方法主要通过运动补偿进行帧间预测，而同步辐射光源实验中样品的运动轨迹是绕中心轴旋转，基于运动的帧间预测方法不适用于该场景。

本文提出了一种基于差分和神经网络的同步辐射光源图像无损压缩方法。首先基于图像序列之间的强相关性，通过图像差分去除图像间线性冗余；然后对差分图像进行截断映射，解决了原神经网络压缩方法对16 bit数据没有明显压缩效果的问题；为消除模型大小对图像压缩率的影响，对一组图像序列使用统一模型进行预测压缩，得到的压缩率优于传统图像压缩方法；最后，为优化压缩时间，对差分映射图像进行像素位分裂，并行化处理以加速图像压缩过程。

1 相关工作

1.1 传统无损压缩方法

通用无损图像压缩方法主要通过消除图像局部的相似性，并结合编码进行压缩。便携式网络图形[2](portable network graphics，PNG)通过差分去除图像内部冗余，使用Deflate对剩余信息进行压缩；JPEG2000[3]将原始图像分割成互不重叠的图像块，以块为单位进行离散变换，将得到的变换系数作为量化和熵编码对象；自由无损图像格式[4](free lossless image format，FLIF)基于元自适应近零整数算术编码(meta-adaptive near-zero integer arithmetic coding，MANIAC)，通过构建决策树学习上下文模型。对于标签图像文件格式(tagged image file format，TIF)图像，常见的压缩方法为串表压缩(lempel-ziv-welch encoding，LZW)算法和位压缩(PackBits)算法，LZW算法通过建立字符串表，用较短的代码表示较长的字符串来实现压缩；PackBits算法通过字节重复或不重复个数来减少字节的数量，达到压缩的目的。JPEG-LS[5]常用于医学图像无损压缩。上述方法只能通过去除单个图像内部冗余的方法以减小图像体积。

FFV1[6]是一种无损视频编码格式，通过上下文模型进行视频压缩，根据相邻像素预测当前像素值，通过熵编码压缩真实值和预测值之间的差异;文献[7]提出一种基于差分和JPEG2000的压缩方法，用于处理红外探测系统产生的图像序列，对于序列中单张图片的某一像素值，将其左侧相邻像素值或前一张图像同一空间位置像素作为预测值，使用JPEG2000压缩真实值与预测值的差。经测试，该方法对于同步辐射光源图像压缩结果没有明显提升，这是由于相较于红外图像，同步辐射光源图像更为复杂，虽然差分后像素值分布会更加集中，但是JPEG2000无法挖掘更深层次的相关性来降低图像所需存储空间。

1.2 基于神经网络的压缩方法

神经网络包含卷积神经网络和循环神经网络等，卷积神经网络为包含卷积计算且具有深度结构的前馈神经网络，循环神经网络在网络结构设计上引入了时序的概念[8]，能对输入时序信号逐层抽象并提取特征[9]。神经网络目前已经在诸多场景中有了广泛应用和突破，比如机器翻译[10]、语音识别[11]、摘要提取[12]等。而在数据压缩方面，传统压缩方法无法对于特定数据进行优化，因此研究人员在基于学习的图像和视频压缩方向进行了诸多研究。

1.2.1 有损压缩

基于神经网络的有损压缩方法主要通过构建自编码器和自回归模型等达到压缩的目的。文献[13]通过自编码器学习图像数据分布到潜在空间的可逆映射，其潜在空间经过量化，最终压缩量化后的潜在空间以有损压缩数据。文献[14]通过循环神经网络增加感受野，以感知更大图像区域的信息；文献[15]构建基于神经网络的自编码器进行视频压缩，利用先验信息优化压缩效果；自回归模型通过上下文建模预测图像概率分布，目前主流的回归模型包括PixelCNN[16]、PixelCNN++[17]、PixelRNN[18]以及Multiscale-PixelCNN[19]等。文献[20]提出一种通过卷积神经网络(convolutional neural network，CNN)学习原始图像紧凑表示，用于优化遥感图像数据的传输过程。文献[21]通过变分自编码器模型实现了连续比特率可调的图像压缩方法。文献[22]综述了基于神经网络的视频压缩方法，该类方法主要通过构建不同的神经网络结构以预测运动矢量，并用于构建后续预测帧。基于运动补偿的方法更适用于平移等线性移动的帧间预测，而同步辐射光源图像中样品运动为绕中心轴旋转，像素值为多个点旋转后的复合值，即单一像素值变化与同一行左右像素值相关，不能简单地通过运动补偿进行预测。

1.2.2 无损压缩

而神经网络在无损压缩方面也极具潜力。由信息论可知，数据压缩的极限与信源各元的概率分布以及信源各元之间的相关性有关。对于不同的压缩方法，同一信源各元之间的相关性是固定不变的，因此压缩方法的效果与概率分布相关，概率分布指的是一定长度的数据中各元的概率分布情况，理论上，当长度为1时，仅该元真实值对应概率为1，其余值对应概率为0，此时能够得到最好的压缩率。而获得下一个元真实值的概率有两种方式：一是直接记录下一个元取值的概率分布，这种方法会引入与信源长度相同的概率分布数据，无法达到压缩信息的目的；二是通过前向序列推测下一个元的概率分布，推测的过程通过神经网络实现，因此神经网络学习能力越强，预测越准确，从而获得更好的压缩率。理想情况下，模型学习能力达到根据前向序列推测出当前元正确的值，当前元被正确推测出之后，可用于后续元的推测，此时数据压缩的边界大小仅为模型大小以及一段常数长度的前向序列。

文献[23-24]将神经网络用于RGB图像无损压缩，通过保存图像的低分辨率作为输入，以预测高分辨率图像的概率，结合熵编码达到无损压缩的目的。文献[25]将神经网络用于文本序列无损压缩，通过神经网络挖掘数据内部的非线性关系，通过前向序列值来预测当前值在字典上的概率分布，其中字典由文本中出现的所有字符构成，最后结合算术编码进行压缩，该方法在DNA等字典较小的数据上得到了优于传统方法的结果。但该方法需要对每一个压缩对象训练独立的模型，并且压缩时间较长，针对该问题，文献[26]提出一种混合自适应训练和半自适应训练的架构，但是该方法在光源图像压缩问题上表现不佳；另外，对于16 bit的同步辐射光源图像，存在字典范围较大情况下压缩不明显的问题。同样将神经网络用于无损压缩的新方法还包括lstm-compress[27]，该方法可直接用于16 bit数据压缩。

2 图像压缩方法

2.1 图像特点

同步辐射光源装置生成的图像是16 bit单通道灰度投影图像序列，像素值代表该像素上光子数的多少。对任意样品，投影图像像素数目一般为M2，图像张数最少为M×Π/4(Π取3.14)，具体取值与设备和样品有关，单个样本会产生上千甚至上万张图像，数据量达到数GB，这些图像具有高帧率、高分辨率和低对比度的特点。如图1所示，示例图像中的样品为恐龙尾巴，图像中样本结构复杂，相互重叠，图像尺寸为1 200×2 048，扫描共产生1 622张投影图，图像像素值主要分布在0～40 000之间。

由于拍摄样品投影图时，相邻拍摄之间会对样品旋转一个极小的水平角度，同时样品本身具有结构信息，因此光源图像序列在时间和空间上存在一定的相关性。其中空间相关性指图像内部某像素与相邻像素之间的相似性，使用自相关系数衡量，对于尺寸为X×Y的图像，空间相关性计算公式为：

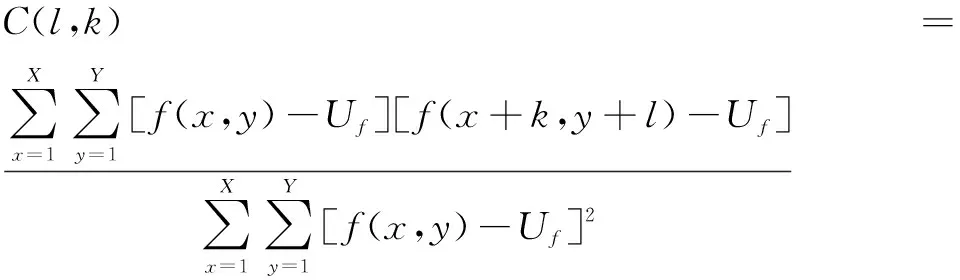
(1)

其中，l为左侧间距，k为上方间距，Uf为图像像素值均值，f(x，y)为图像对应位置的像素值。

(a) 示例(a) Example

时间相关性指连续两张图像同一空间位置像素之间的相关性，使用互相关系数衡量，计算第i张图像与第j张图像的时间相关性公式，即：

(2)

对上述示例图像序列，计算其图像之间的时间相关性以及图像内部的空间相关性。其中，时间相关性分别取待计算图像的前2n(0≤n≤6)张图像进行计算，空间相关性分别取间距为2n(0≤n≤6)的左、上、对角位置像素值进行计算，取均值后得到结果如图2所示。

图2 原图时间及空间相关性系数Fig.2 Temporal correlation and spatial correlation of original images

由图2可知，该图像序列时间相关性接近于1，说明该图像序列具有极强的时间相关性，其中时间相关性大于空间相关性，而空间相关性整体较弱，不同位置元素相关性的差异随着n的增大而增大，其中，左侧元素相关性相对较强，同时随着n的变化下降最缓慢，对角元素相关性最弱；同时，随着间隔变大，时间相关性和空间相关性均呈下降趋势。因此，对于原图设计了两种差分方式：一是时间差分，即将前一张图像同空间位置的像素值作为预测值；二是空间差分，即选择左侧元素的像素值作为预测值。

2.2 压缩流程

本文提出的同步辐射光源图像无损压缩方法如图3所示。首先对于原始图像序列进行差分，以去除图像序列的线性相关性，差分分为时间差分和空间差分，时间差分即相邻两张图像同一空间位置像素相减，序列中第一张图像不做处理，空间差分即从图像第二列开始，像素值减去左侧相邻元素原始像素值。然后训练神经网络挖掘差分图像序列内部的非线性相关性，将像素分布范围作为字典取值范围，使用训练好的模型以预测像素值在字典范围内的概率分布，结合算术编码进行压缩，其中为了解决字典过大导致的压缩效果不明显的问题，提出可逆的截断映射方法以大幅缩小数据范围，对于压缩过程耗时问题，提出像素位分裂策略，将像素值分裂为高位和低位两部分并行处理。解压为压缩的逆过程，读取压缩时保存的模型参数初始化模型，保证解压得到的数据与原始数据相同，最终达到无损压缩的目的。

图3 光源图像压缩流程Fig.3 Dataflow of the compression method

2.3 图像差分与截断映射

图像差分用于减弱图像间或图像内部的相似部分，突出不同部分，分为时间差分和空间差分。以时间差分为例，如图4所示，第一行图像从左到右为原始图像序列，第二行图像为对应上方原始图像减去前一张图像空间位置像素值后得到的时间差分图像，为对比明显，将原图和时间差分映射后的图像由16 bit转换到8 bit。原始图像由于对比度低，样本轮廓模糊，同时，由于图像像素值代表平行光透过样品后的光子数，所以包含样品信息的部分像素值较小，而不含样品信息的部分像素值较大。经过时间差分后，图像中样品的特征更加明显，包含样品信息的部分像素值增大，而由于前后相邻图像中样本信息含量较少的部分像素值比较接近，因此减弱了噪声信息对样本信息的干扰。

图4 原始图像与时间差分映射图像对比Fig.4 Original images and temporal-difference mapping images

截断映射用于进一步缩小差分图像的像素值分布范围，该映射是可逆的。经过差分后，图像像素值分布更加集中，因此，压缩过程中选择不压缩部分长拖尾数据值，将其统一映射到新的像素分布范围右侧边界加1的值，原始数据按顺序直接存放至压缩数据流末尾，即将数据分为不压缩和待压缩两部分，用较小的空间代价换取更小的数据分布范围，定义该过程为截断映射。新的数据分布范围以0为起始点，因此映射后待压缩数据均为非负值，确定分布范围终点时，首先将数据右移一段距离，这段距离是新的数据分布范围的中轴对应值，然后判断在这个范围内是否包含了超过98%的数据，当判断成功时即获得了新的分布范围。

选定像素值范围界限如式(3)所示。像素值分布整体向右平移Bound(index)/2后，统计像素值落在[0,Bound(index)]中的百分比，当百分比大于98%时即获得截断映射的边界范围值。

(3)

以上述差分图像为例，可得Bound为3 000，说明差分图像像素值98%以上在[-1 500,1 500]之间。将在范围内的数据平移到[0,3 000]，同时将范围外像素值使用3 001替代，图5为将数据范围进一步缩小到[0,3 001]之后的数据分布图，末尾为压缩过程中不压缩的数据量。

图5 时间差分映射图像像素值分布Fig.5 Pixel value distribution of temporal-difference mapping image

经过差分后，图像的时间相关性和空间相关性会发生变化，两种差分方式均可有效去除图像序列中存在的时间冗余和空间冗余。以经过截断映射的空间差分图像为例，如图6所示，图像的时间相关性和空间相关性相较原图大幅度减小，其中时间相关性降低到0.4以下，不同位置空间相关性降低到0.2以下，随着n的增大，时间相关性降低到0.2以下，空间相关性趋近于0。因此，差分操作可以有效降低图像序列内的线性时间相关性和空间相关性。

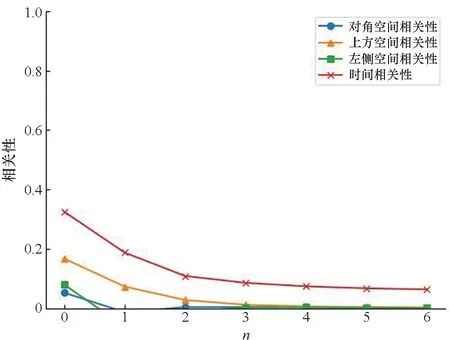
图6 空间差分映射图像相关系数Fig.6 Correlation factor of spatial-difference mapping images

2.4 模型输入输出构造

模型的输入来源是差分映射图像、对应时间相关性和空间相关性，模型的输入分为两种，即时间序列和空间序列，输入输出构造如图7所示。以预测T时刻图像某一像素值(即图7(c)中T时刻红色像素块)概率分布为例，时间序列为前K张图像中与预测像素值空间位置相同的像素按时间顺序排列得到的输入序列，图7(a)为K=3的情况；空间序列为待预测像素块左上方共N×(N-1)个像素块按行扫描顺序排列的输入序列，图7(b)所示为N=2的情况。

(a) 时序输入构造(a) Construction of input in temporal

模型输出是一个长度与图像像素取值个数相同的稀疏向量，向量中每一个元素值的大小代表当前像素取值与对应元素相同的可能性。训练时构造的输出如图7(c)所示，该向量仅在预测像素值对应位置为1，其余位置为0；预测时，模型的输出为预测值的概率分布。

2.5 模型结构

将经过差分映射后的图像数据看作文本序列，使用嵌入层将输入转换为具有特定大小的向量，随后输入神经网络进行处理，输出层为softmax，输出为待预测像素值的概率分布。模型训练基于Tensorflow[28]、sklearn[29]等框架，损失函数选用交叉熵损失函数。以三种神经网络结构作对比：全连接层(fully connect layer，FC)、长短时记忆网络(long short-term memory，LSTM)、门控循环单元(gated recurrent units, GRU)。

FC中，当前层每一个节点均与上一层每个节点连接，由自身反向传播确定准确的权重。每个神经元接收的权重将优先选择最合适的标签，最终，综合神经元在每个标签上的选择得出结果。

LSTM使用时间记忆单元记录当前时刻的状态，一般称为长短期记忆神经网络的细胞。每个细胞与三个信息传递开关门相连接，分别是遗忘门、输入门和输出门，以共同控制信息流入和流出，“门”机制解决了循环神经网络的梯度消失问题，从而学习到长距离依赖。

GRU与LSTM都是为了解决长期记忆和反向传播中的梯度等问题，不同于LSTM，GRU只有两个门用于控制信息的传递，即更新门和重置门，因此网络结构更加简单，更易训练，能够很大程度上提高训练效率。

2.6 像素位分裂

像素位分裂即将像素值所占比特位分为高位和低位两部分并行处理。由于循环神经网络压缩方法用时较长，因此探索在保证压缩率不受影响的前提下，像素位分裂对于本方法加速的空间。

相较于分裂之前，将差分和截断映射后的图像像素值分裂后，可以得到更规律的高位像素值分布，分裂之后的可以得到更规律的高位像素值分布，而低位像素值随机性更强，这是因为光源图像经过差分和截断映射后，包含样本信息的像素值变大，噪声部分集中在数据的低位，所以像素值高位数据包含更强的样本结构信息，可学习性更强，训练得到的模型预测效果会更好，虽然低位数据包含噪声，随机性更强，导致可压缩空间降低，但是经过像素位分裂之后，低位数据所占比特位进一步缩小，因此其像素值范围可以得到进一步减小，此外，高位数据可压缩空间变大，一定程度上可以缓解甚至弥补低位可压缩性变差的问题。

像素位分裂后，像素值预测可以分为两部分并行预测，同时减小像素值范围，缩短模型预测和编码过程所需时间，在不影响分裂前压缩率优化效果的前提下，对压缩过程进行加速。

3 方法验证

3.1 数据集准备

数据集来自上海同步辐射光源扫描样品得到的图像序列，如图8所示。图像大小为1 200×2 048，每张图像4.68 MB，共1 622张。对图像进行差分和截断映射，得到时间差分映射图像和空间差分映射图像。由于同一图像序列相似度较高，相邻图像压缩率相近，因此每隔100张选取一张图像进行压缩测试，共16张图像。

图8 数据集示例Fig.8 Dataset example

由于压缩的目的是为节省存储空间，这里定义压缩率为压缩后整体大小与原图像大小之比，压缩率越小，所需存储空间越小。由于截断映射后，图像数据分为待压缩和直接存放两部分数据，因此压缩后图像大小为不压缩部分的大小与待压缩部分压缩后大小的和，整体大小为压缩后图像大小与训练得到的模型参数大小的和。

3.2 基准测试

本文使用的基准方法中，图像无损压缩方法包括PNG、JPEG2000、JPEG-LS、TIF的压缩方法以及视频无损压缩方法FFV1，同时增加通用无损压缩方法gzip、bzip2以及神经网络无损压缩方法lstm-compress进行压缩率对比。对于测试数据集使用上述无损压缩方法进行压缩，计算压缩率并取均值。

结果如图9所示，TIF格式常用压缩方法LZW和PACKBITS没有压缩效果，gzip和PNG压缩结果在80%以上，bzip2、JPEG2000、FLIF以及FFV1的压缩结果均在70%以上，而基于神经网络的压缩方法lstm-compress的压缩结果为76.72%。其中，最优压缩率是由JPEG-LS方法压缩得到的结果69.77%，以此作为后续对比基准。

图9 不同图像无损压缩方法的压缩率Fig.9 Compression ratio of different image lossless compressed methods

3.3 结果与分析

模型训练epoch设置为5，当epoch达到最大值或者损失函数值连续三次不下降时结束训练，使用随机种子随机化设置隐藏层中的权重值和偏差值，Adam更新网络中的参数。分别对测试数据构造时间输入序列和空间输入序列，与基准测试结果进行比对，得到差分方法和输入序列构造方法的最优组合方式，然后对比该结果与像素位分裂后的压缩率和压缩时间。

3.3.1 模型输入选择

由于差分方式和构造方式的差异，可以得到四种模型输入：时间差分映射图构造时间序列、时间差分映射图构造空间序列、空间差分映射图构造时间序列、空间差分映射图构造空间序列。

为对比不同输入构造下的压缩结果，时间序列与空间序列选取相同的长度，时间序列长度为K，空间序列长度为N×(N-1)，K与N均为正整数，因此K=N×(N-1)。此处选择FC对单张图像进行预测压缩。四种输入构造方式结果对比如图10所示。

(a) 时序输入压缩率(a) Compression ratio of input in temporal

对于时间序列构造方式，随着K取值的增大，压缩率呈下降趋势，当K增大到一定程度，压缩率变化不明显；在这种序列构造方式下，时间差分映射图像的压缩率优于空间差分映射图4%～5%。对于空间序列构造方式，随着N的增大，压缩率呈先下降后上升趋势，对于时间差分映射图像，压缩率在64%以上，随着N的增大，压缩率在70%左右，对于空间差分映射图，压缩率变化相对稳定，结果为70%左右。因此，时间序列结合时间差分的构造方式得到的压缩率提升是最优的，图片压缩率在45%左右，相较于FLIF降低25%。

但是模型本身的大小会抵消部分压缩效果，因此需要对于一组图像使用统一模型进行压缩，以减小模型大小对最终压缩结果的影响。

3.3.2 统一模型压缩验证

对每一张图片建立的独立模型方式会消耗一定的时间和空间，模型训练时间大于图像压缩的时间，以时间差分映射图K=8的时间序列构造输入训练得到的模型为例，不同模型大小不同，FC模型为2.4 MB左右，LSTM与GRU模型为1.2 MB左右。为保证无损压缩，模型参数需作为压缩后图像的一部分进行保存，模型大小严重影响甚至抵消了图像的压缩效果，因此需要对多张图片建立单一模型。由于同一样品得到的图像序列相似度较高，所以不同于上述对于每一张图像建立一个模型的方法，仅使用单个样品的图像序列中的单张图片建立一个模型，测试对于单个样品的整个图像序列的压缩结果。这里选择16张图片中的第1张，通过时间差分和截断映射后构造时间序列，其中K=8，训练得到不同的模型(FC/LSTM/GRU)，对16张图片进行压缩，压缩率如图11所示。

图11 16张图片的压缩率Fig.11 Compression ratio of 16 images

对于不同模型，压缩率变化趋势和大小非常相近，LSTM与GRU最接近，FC压缩率高于另外两个模型，说明在同步辐射光源图像序列压缩任务上，GRU与LSTM表现类似于其他深度学习任务，而两者对于时序数据具有较强的学习能力使得其能够达到比仅使用FC更好的效果，也说明通过消除时间冗余信息能够进一步优化同步辐射光源图像的压缩效果，同时，三者压缩率的趋势变化是相似的，说明在该任务下，三种模型的泛化能力相似。

该方法整体压缩率在46%上下震荡，最低46%，最高52%，对比传统无损压缩方法，有20%以上的提升。三种神经网络模型均在光源图像压缩上表现出低于传统图像无损压缩方法的压缩率。

将本文提出的方法中神经网络结合算术编码部分替换成传统算术编码进行对比，传统算术编码中，编码概率分布通过统计全部图像像素值的概率分布获得。将经过差分和截断映射后的图像通过算术编码方法[30]进行压缩，并与本文提出的方法进行对比。对于上述测试图像通过传统算术编码压缩后得到压缩率结果为72.98%，因此本文引入神经网络是优化同步辐射光源图像压缩率的有效方法。

3.3.3 像素位分裂

考虑将像素位分裂为两部分并行压缩，由于差分映射阶段像素值范围被压缩至[0,3 001]，因此，像素值所需比特位为12位，像素值分裂为高Q位和低(12-Q)位，Q∈[2,4,6,8,10]，选择时间序列构造方式K=8，N=1，FC模型，测试五种分裂方式下压缩结果和压缩时间的变化情况。

位分裂后图像序列的压缩率如表1所示。由于数据分为高位和低位两部分，因此压缩率为两部分压缩率之和，最优的分裂为高2位和低10位，随着分裂位置右移，压缩率总和呈先上升后下降的趋势；高位压缩率呈上升趋势，上升幅度越来越小，说明当分裂位置右移时，模型对于高位数据的变化情况学习能力越来越差，这是因为随着分裂位置右移，加入了更多环境噪声的影响，同时像素范围也进一步增大；低位压缩率在前三种方式中差距较小，随着像素值范围的缩小没有产生明显变化，去除掉高位包含样本信息较多的数据后，低位数据更加复杂，而后随着像素值范围的进一步缩小，压缩率有所下降。对于最优的分裂方式，压缩结果与分裂前压缩结果接近，为46%。

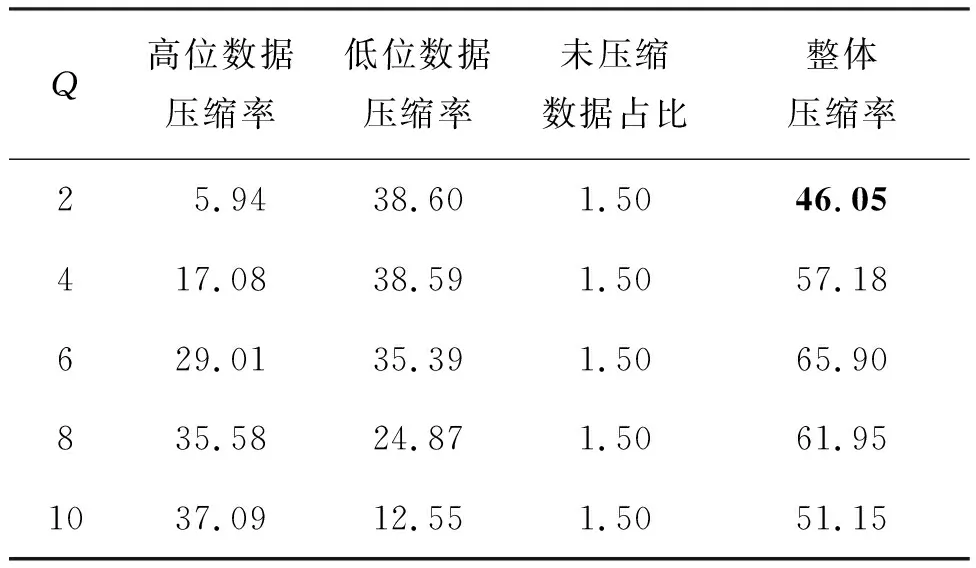
表1 不同分裂方式下的压缩率

整个压缩过程分为三个阶段：构建模型输入、模型预测和算术编码，而模型输入构建过程极短，模型预测和编码阶段是压缩时间的主要组成部分，主要耗时阶段是模型预测和编码阶段，各阶段耗时如图12所示。

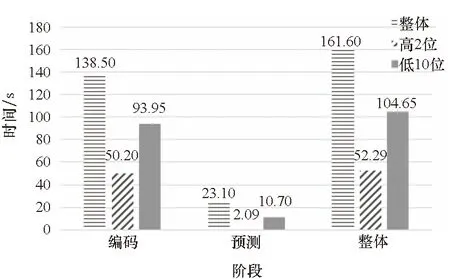
图12 各阶段耗时Fig.12 Time-consuming of different stages

由图12可知，像素位分裂后预测时间和编码时间均小于分裂前用时，高低位处理的时间之和与原始用时相当。由于并行操作，分裂后压缩需要的时间总和为低位压缩用时，较原压缩方式节省1/3的时间。所以，位分裂操作可以有效缩短压缩过程中的编码时间和预测时间。

因此，对于光源图像序列，位分裂操作能够在不影响分裂前图像压缩率的同时节省30%以上的压缩时间。

4 结论

本文提出了一种基于图像差分和神经网络预测的光源图像压缩方法，验证了差分方法对于压缩结果的有效性，其中，通过差分和截断映射，有效降低像素值所占比特位，大大缓解了神经网络对于16 bit数据压缩困难的问题。此外，不同于传统无损压缩方法通过统计一定长度数据的概率分布，该方法通过神经网络仅预测后续单个像素值的概率分布，最终得到的压缩率比传统无损图像压缩方式节省20%以上的存储空间。最后，通过像素位分裂方法探索通过该方法进行并行加速的同时能否保证压缩率优化效果不受影响，对比基于神经网络的压缩方法在像素位分裂前压缩用时，该方法可以在保证压缩率优化效果的前提下降低30%压缩时间。

后续可以尝试更多不同的网络结构进行压缩测试，引入视频插值和视频超分辨率的技术代替差分模块，从空间维度和时间维度进一步探索图像压缩的潜力。由于预测方法中同一张图像的像素值预测编码具有相互独立性，后续可以通过分块并行减少图像压缩时间，同时，可以结合神经网络剪枝算法等进一步优化模型预测时间。

致谢

本文的数据处理得到了国家高能物理科学数据中心和中国科学院高能物理数据中心提供的计算和数据资源支持。