拖缆与OBN资料联合成像域最小二乘逆时偏移成像
2022-10-04杨华臣张建中
杨华臣, 张建中,2*
1 海底科学与探测技术教育部重点实验室, 中国海洋大学海洋地球科学学院, 青岛 266100 2 青岛海洋科学与技术国家实验室, 海洋矿产资源评价与探测技术功能实验室, 青岛 266061
0 引言
拖缆地震是海洋油气勘探的主要技术(Rickett,2003;刘学建和刘伊克,2016;叶月明等,2019;张瑞等,2020),具有施工效率高、采集成本低和覆盖次数高等优点.在地质结构较为简单的地区,仅使用拖缆地震资料就可以获得高质量的偏移成像剖面(韩复兴等,2015;张力起等,2019;段心标等,2020).然而,在存在高陡构造、古潜山等深部地质构造复杂的区域,地震波场复杂,因拖缆的长度有限,难以记录深部地层的反射波信号,使得深部地层的偏移成像效果不佳,无法正确刻画深部的复杂地质构造(Wong et al.,2012;Zhang and Schuster,2013;Li et al.,2017;张振波和罗伟,2021).
海底地震是新发展起来的海洋地震勘探技术(Sollid and Ursin,2003;Zhang,2014;赵维娜等,2019).震源在近海面被拖拽着激发,海底地震节点(OBN)放在海底接收,其偏移距可以达到数十千米,能够记录到深部高陡构造的反射波信号,对深部的复杂地质构造进行有效成像(Zelt et al.,1998;Charvis and Operto,1999;Wong et al.,2011;Wang et al.,2012;Cheng et al.,2018).然而,OBN资料采集的施工周期较长、成本高.为了减少OBN资料采集的成本,通常布设OBN的间距较大(Wong et al.,2012;钟广见等,2014;赵维娜等,2019,2020),导致OBN资料对海底介质的覆盖次数较低,且在空间上的照明分布非常不均匀(Zhang et al.,2019),在某些浅部地层甚至没有覆盖,从而使得OBN资料的偏移成像剖面,特别是对浅层的成像质量较差(Zelt et al.,1998;Wong et al.,2011,2012;钟广见等,2014).
一般地,拖缆地震资料对浅部地层的覆盖次数较高,OBN资料对深部地层的覆盖次数相对较高,这两种地震资料具有优势互补性.我们联合使用拖缆与OBN资料进行波形反演,获得了比使用其中一种资料更好的效果(Yang and Zhang,2019).Wong等(2012)利用一个理论模型合成资料,说明了存在钻井平台等障碍物时拖缆与OBN资料联合偏移成像的优势.可见,联合使用拖缆与OBN资料进行偏移成像,可以有机地发挥两种资料的优点,克服缺点,获得更高质量的偏移成像效果.因此,本文研究一种拖缆与OBN资料联合的最小二乘逆时偏移成像方法(LSRTM).
此外,常规数据域LSRTM需要通过多次偏移与反偏移来估计Hessian矩阵(Ji,2009;Di et al.,2016;王晓毅等,2021),计算量大,联合使用拖缆与OBN资料时该问题更严重.本文的拖缆与OBN资料联合的LSRTM,通过在成像域计算点扩散函数来估计Hessian矩阵,无需进行多次偏移和反偏移运算,极大地提高了LSRTM的效率.将本文方法应用于复杂构造模型的合成资料,验证了联合LSRTM对于诸如高陡构造等复杂地质构造的成像优势.
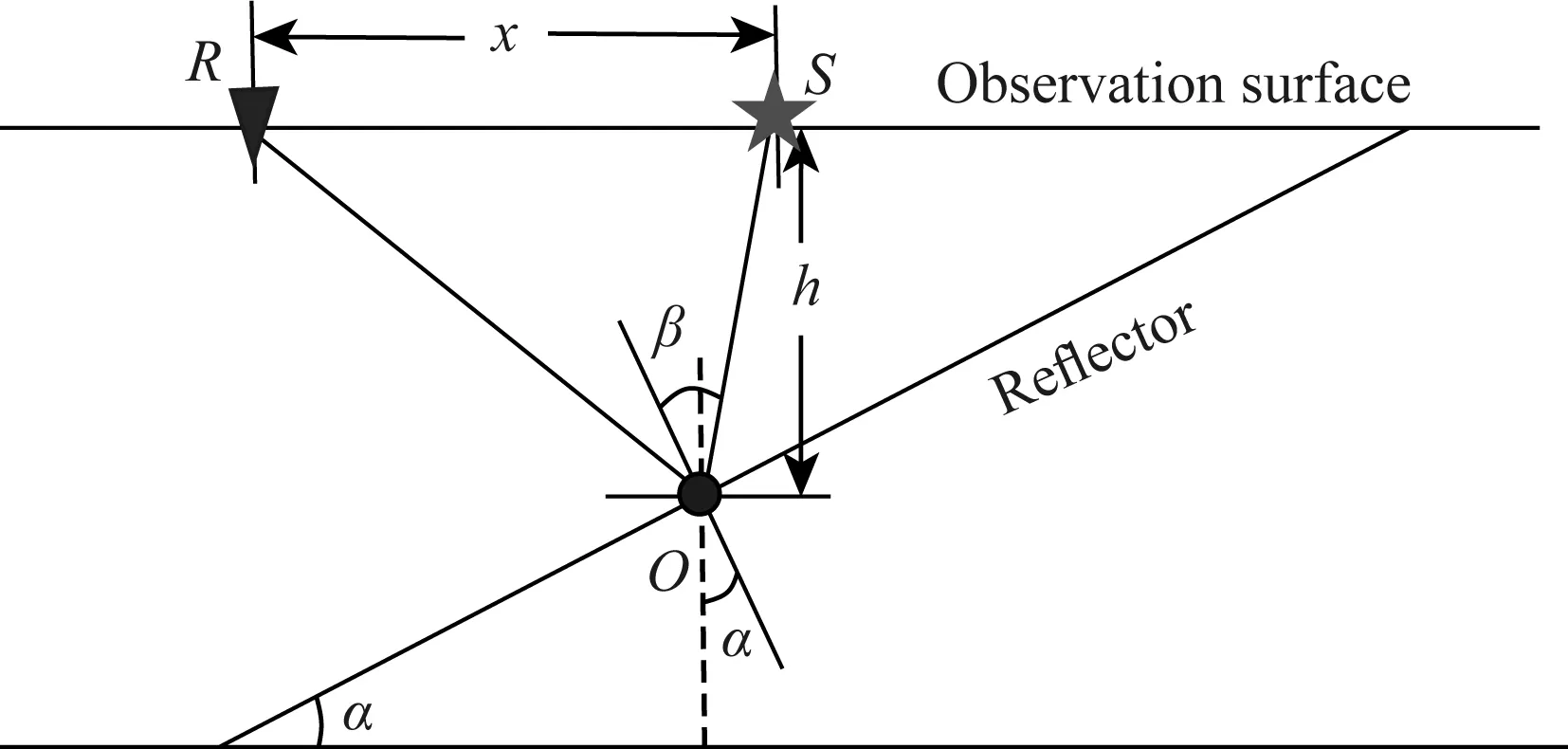
图1 倾斜界面反射波射线路径示意图五角星表示震源,三角形表示检波点,圆点表示反射点. α、β、h和x分别表示反射界面倾角、入射角、反射点深度和偏移距.Fig.1 The ray path of the reflection wave with a sloping reflectorThe star, triangle, and dot indicate the shot, receiver, and the reflection point, individually. The α, β, h, x indicate the dip angle of the reflector, incident angle, depth of the reflection point, and offset between the shot and receiver, respectively.
1 拖缆资料偏移成像的问题
因拖缆的长度有限,拖缆地震采集系统的偏移距不够大,难以记录高陡构造的反射波信号.图1是一个倾斜界面及反射波射线路径示意图.S为炮点,R为接收点,反射点位于O点,界面倾角为α,偏移距为x,反射点深度为h,入射角或反射角为β.这些参数之间存在如下关系:
x=h[tan(β+α)+tan(β-α)],
(1)
当α=β=0时,x=0,此时界面水平,反射波垂直入射到反射界面并返回,为水平反射面的自激自收情形;当α≠0,β=0时,x=0,为倾斜反射面的自激自收情形;当α+β=90°时,x趋于无穷大,反射波从反射点沿水平方向向左传播,在观测面不能接收到反射波信号.因此,在观测面接收到的反射波的反射角β必介于0°与90°-α之间,且α越大,x将越大.
图2是用式(1)计算的偏移距x随反射界面倾角α、反射点深度h以及反射角β的变化曲线.图2a表明,当h=4 km,β=30°,α<40°时,偏移距x随α增加而逐渐从约4.6 km增加到约10.3 km;当α>40°,x随α增加而急剧增加.α=25°对应的偏移距x=6.06 km.这说明,当地层倾角大于25°时,偏移距x小于6 km的拖缆检波器接收不到反射波.从图2b看出,当α和β一定时,x随h增加而线性地增加.当α=50°,β=30°时,要接收到来自深度h=1.2 km的反射波,偏移距x不能小于6.4 km.图2c表明,当α=50°,h=4 km时,x随β增加而增加,且增加的速率逐渐变大.β越大,炮点离反射点水平距离越大,接收到反射波的偏移距也越大.当α=50°,h=4 km时,β=16°对应的偏移距x=6.29 km.这表明,反射角大于16°的反射波不能被长度为6 km的拖缆中的检波器记录到.综上,反射界面倾角α、反射点深度h或反射角β增加都会使偏移距x增加.因此,只有在偏移距达到一定程度时,才能记录到深部高陡构造的反射波信号.然而,常规的拖缆长度通常在6 km左右(马光克等,2019;张振波和罗伟,2021),难以记录深部高陡构造的反射波信号,导致其偏移成像孔径小、成像效果差.
2 联合成像方法
2.1 基本原理
为了联合使用拖缆与OBN资料进行LSRTM,获得地下介质的反射率成像剖面,定义联合LSRTM的目标函数为:
(2)

为了获得目标函数的极小值,令其对反射率模型的一阶导数为零,可得:
(3)
其中,LT表示偏移算子,LTd表示观测地震记录的逆时偏移成像剖面,LTL为Hessian矩阵.
采用声波方程进行偏移与反偏移(刘梦丽等,2018;柯璇等,2019).为了压制逆时偏移成像剖面中的低频背景噪声,采用上下行波分离的互相关成像条件(Liu et al.,2011):
+pu(x,t|xs)qd(x,t|xs)]dt,
(4)
其中,I表示逆时偏移成像剖面,s表示震源序号,T表示地震记录最大采样时间,pu和pd分别表示震源正向传播波场的上、下行波,qu和qd分别表示检波点反向传播波场的上、下行波,x表示空间坐标,xs表示震源的空间坐标,t表示时间.在波数域进行上下行波分离,具体方法请参见Liu等(2011).
将式(3)改写为下列形式:
Hm=mmig,
(5)
式中:
(6)
(7)

(8)
(9)

通过式(6)和式(7)分别求得H(H的计算方法在下一节介绍)和mmig后,采用阻尼最小二乘算法求解式(5),得到反射率模型m.
2.2 计算Hessian矩阵
式(5)中Hessian矩阵很大,直接计算和存储Hessian矩阵是非常困难的(Tang,2009;李振春等,2014).传统的数据域LSRTM通过多次偏移和反偏移来估计式(5)中的Hessian矩阵(刘梦丽等,2018;柯璇等,2019).例如,刘梦丽等(2018)和柯璇等(2019)分别在模型试验中进行了30次和50次偏移和反偏移运算,从而使传统数据域LSRTM极其耗费时间.本文通过计算点扩散函数来求取Hessian矩阵,仅需要进行1次偏移和反偏移运算.
式(5)表明,如果已知反射率模型和对应的逆时偏移成像剖面,则Hessian矩阵可以作为未知量求出.因此,如果给定一个反射率模型,并通过逆时偏移成像方法获得其对应的像,则可以通过阻尼最小二乘算法等求解式(5),获得Hessian矩阵.
特别地,当反射率模型m中仅第i点存在扰动,即反射率模型中仅第i个元素为非零值,逆时偏移成像后该点对应的像为Hessian矩阵中第i列的元素.此时,式(5)可以表示为:
(10)
其中,n表示反射率模型中元素的总个数,mi表示仅第i个点存在扰动时的反射率模型,即:
(11)
式中,η是一个给定的小量,本文设置为0.01.
将式(11)代入式(10),进行矩阵相乘,可得:
(12)
式中,等号右端是mi对应的像,可以使用逆时偏移成像方法得到.因此,通过式(12)就可以得到Hessian矩阵H中第i列的元素.该列元素体现了第i个点的反射率与其像之间的映射关系,即该点的点扩散函数.为了简洁,将式(12)记为:
(13)

由于地震波的频带有限,第i个点的像仅存在于该点邻域内(以第i个点的位置为中心两倍波长为半径的区域内),在远离该点的区域其成像值为零.因此,可以在反射率模型m中同时设置若干个空间上具有一定间距的散射点,并给定其扰动,再通过逆时偏移成像方法得到它们的像,即它们的点扩散函数.最后,通过插值方法得到反射率模型向量m中任意一点的点扩散函数.求得每一点的点扩散函数后,就获得了Hessain矩阵中每一列的元素.此时,式(5)中的Hessian矩阵可以表示为:

(14)
当速度模型存在速度突变界面时,逆时偏移成像剖面中通常会存在一定的低频背景噪声(杨仁虎,2021;诸峰等,2022).这些低频背景噪声与点扩散函数存在明显的差异.点扩散函数在空间上分布相对较为稀疏,表现出高波数的特点.因此,通过对逆时偏移成像剖面进行高通滤波,就可以实现对低频背景噪声的压制,得到准确的点扩散函数.
3 模型资料试验分析
3.1 资料合成
基于Marmousi2模型,建立了2个速度结构相同但模型尺寸不同的速度模型,如图3所示(模型左右两侧12.5 km区域内拖缆与OBS资料的覆盖次数较少,故仅显示了模型中间部分).两个模型在Z方向的大小均为5.375 km,在X方向的大小分别为33.75 km和112.5 km.模型的顶部为海水层,其厚度为0.25 km、速度为1.5 km·s-1.海水层之下0.25~1.5 km深度区间分布5个水平匀速层,速度分别为1.7 km·s-1、1.9 km·s-1、2.4 km·s-1、2.8 km·s-1和3 km·s-1.在Z方向1.5 km以下区域存在从Marmousi2模型截取的一系列高陡地层和断层.整体上,图3a模型中深部(Z>1.5 km)地层倾角主要介于12°~46°,图3b模型对应的地层倾角大致介于1.2°~6°.模型的最小和最大速度分别为1.5 km·s-1和5.56 km·s-1.
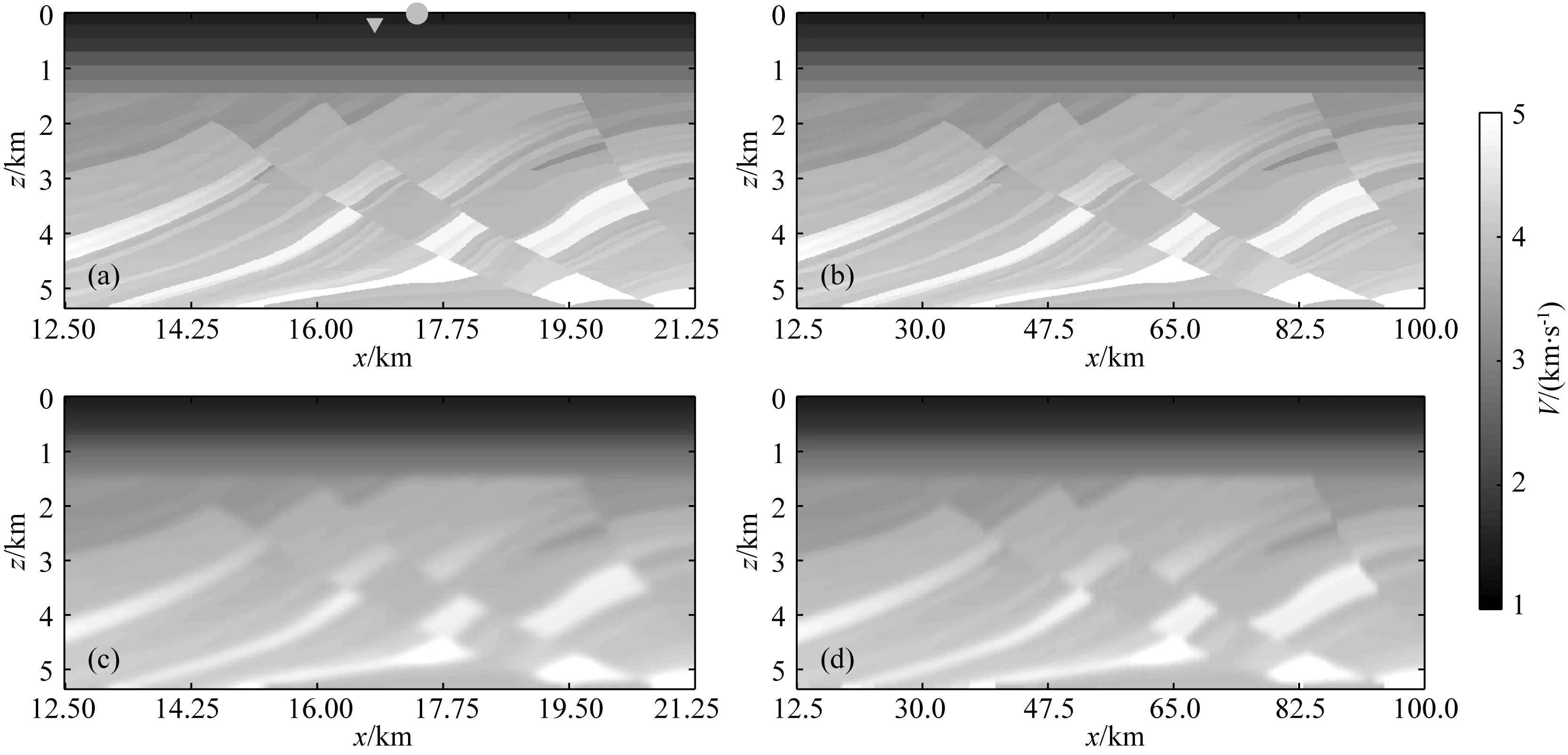
图3 速度模型(a) 小尺寸的理论速度模型;其中三角形和圆点分别代表图4的OBN和炮点的位置; (b) 大尺寸的理论速度模型; (c)和(d) 分别是图(a)和(b)所示模型的平滑速度模型.Fig.3 Velocity models(a) Theoretical velocity model with smaller size; The triangle and dot indicate the OBN and shot location in Fig.4, respectively; (b) Theoretical velocity model with bigger size; (c) and (d) Indicate the smooth version of velocity models shown in (a) and (b), respectively.
在合成拖缆地震资料时,将拖缆长度设置为12 km,道间距为12.5 m,共960道.震源以100 m的间距从模型左侧X=12.5 km处开始激发直到模型的最右侧.拖缆位于震源的左侧,并且随着震源的移动而同步移动.拖缆中的水听器与震源之间的最小偏移距为50 m,最大偏移距为12.05 km.
在合成OBN资料时,将OBN分别以0.4 km、0.8 km和1.6 km的间距均匀布设在海底(Z=0.25 km),震源以100 m的间距从模型最左侧X=0 km处开始激发直到模型的最右侧.
在合成上述两种数据时,均采用边长12.5 m的正方形网格离散速度模型、1 ms的时间采样率和14 s的时间采样长度.使用时间二阶、空间十二阶精度的有限差分方法模拟地震波场(Alford et al.,1974;Liu and Sen,2009).采用PML边界条件压制模型边界处的反射波场(王维红等,2013).考虑到实际资料的频带范围不同,分别采用20 Hz和15 Hz的雷克子波作为震源合成拖缆与OBN资料.
图4a是震源位于海面X=17.4 km处(图3a中圆点所示位置)的拖缆资料炮集记录.图4b是位于海底X=16.8 km处(图3a三角形所示位置)的OBN资料的共接收点道集记录.可以看出,拖缆与OBN资料存在两个重要的差别.第一,拖缆只能记录震源一侧的地震波场,而OBN可以记录震源两侧的地震波场.第二,拖缆只能记录偏移距在12.05 km以内的地震波场,而OBN能够记录到更大偏移距的地震波场信息.这使得OBN资料具有更大的观测孔径,更容易接收到深部诸如高陡构造等复杂地质构造的反射波信号.

图4 合成地震记录(a) 炮点位于图3a中圆点所示位置处的拖缆地震记录; (b) OBN位于图3a中三角形所示位置处的地震记录.Fig.4 Synthetic seismic data(a) Towed-streamer seismic data with the shot located at the dot in Fig.3a; (b) OBN data recorded at the triangle in Fig.3a.
3.2 拖缆资料成像
图3a、b所示速度模型具有相同的地质结构,但中深部的地层倾角不同.分别用125 m×125 m和1250 m×125 m窗口对这两个速度模型进行10次平滑处理,得到平滑速度模型,如图3c、d所示.基于该平滑速度模型,分别对合成的偏移距6 km以内的拖缆地震资料进行逆时偏移成像,结果如图5a、b所示.可以看出,图5a、b中浅部水平同相轴都非常连续、清晰.然而,图5a对中深部的高陡地层和断层反映不清晰、不连续,甚至在局部区域不成像.相比之下,图5b对中深部的地层和断层反映得更清晰、同相轴连续性更好.该测试表明,采用常规的拖缆地震勘探观测系统,对倾斜程度较低的速度界面可以进行较好地成像,而对中深部高陡地层和断层的成像质量较差.

图5 拖缆资料的逆时偏移成像剖面(a)和(b) 分别使用图3a、b所示模型合成的偏移距6 km以内的拖缆地震记录; (c) 使用图3a所示模型合成的偏移距12.05 km以内的拖缆地震记录.Fig.5 RTM images of the towed-streamer seismic data(a) and (b) Using the towed-streamer seismic data with the offset between 0~6 km generated with velocity models shown in Fig.3a,b, respectively; (c) Using the towed-streamer seismic data with the offset between 0~12.05 km generated with the velocity model shown in Fig.3a.
为了分析增加拖缆长度对中深部高陡地层和断层偏移成像的效果,对图3a所示模型合成的偏移距12.05 km以内全部拖缆地震资料进行逆时偏移成像,结果如图5c所示.对比图5a、c可以看出,偏移距长度从6 km增加到12.05 km,中深部高陡地层和断层的成像质量有一定提高,特别是在黑色圆圈所示范围内.然而,相比于图5b,模型中深部高陡地层和断层反映得仍然不够清晰、同相轴不够连续,如黑色箭头所指.这表明增加有限的拖缆长度,对中深部高陡地层和断层成像质量的改善很有限.
3.3 OBN资料成像
基于图3a对应的平滑速度模型,对合成的OBN间距为0.4 km、0.8 km和1.6 km的资料分别进行逆时偏移成像,结果如图6所示.可以看出,中深部的高陡地层和断层均得到了良好地成像.这表明OBN资料能够记录到模型中深部大角度倾斜界面的反射波信号,从而能对复杂的高陡地层和断层进行成像.而且,适度增加OBN间距对中深部高陡构造成像质量的影响相对较小,说明利用稀疏的OBN资料对深部复杂构造进行成像的潜力.但是,OBN间距的增加会降低OBN资料对海底介质的覆盖次数,其逆时偏移成像剖面中有效同相轴的振幅会随着OBN间距的增加而减小,导致偏移成像剖面的信噪比降低.整体上,OBN资料对浅部地层成像效果不佳,且OBN间距越大,偏移噪声越严重.这种偏移噪声主要是浅层介质大角度的反射波和折射波在逆时延拓过程中与震源正传波场互相关产生的.

图6 基于图3a所示速度模型合成的OBN资料逆时偏移成像剖面(a) OBN间距为0.4 km; (b) OBN间距为0.8 km; (c) OBN间距为1.6 km.Fig.6 RTM images of the OBN data generated using the velocity model shown in Fig.3a(a) The interval of OBN is 0.4 km; (b) The interval of OBN is 0.8 km; (c) The interval of OBN is 1.6 km.
3.4 联合成像
采用本文方法基于图3a所示速度模型合成的偏移距6 km以内的拖缆地震记录和接收间距分别为0.4 km、0.8 km和1.6 km的OBN资料进行联合偏移成像.
图7a、b分别是计算的拖缆和接收间距为0.4 km的OBN资料对应的点扩散函数.图中的点状成像区表示一个点扩散函数,反映了该位置处的散射点与逆时偏移成像后的像之间的映射关系,即Hessian矩阵中的一列元素.基于这些离散点对应的点扩散函数,通过插值方法求得空间任意点对应的点扩散函数值,从而得到Hessian矩阵.需要注意的是,在图7a的浅部和图7b的底部存在明显的低频背景噪声.这些噪声会严重影响点扩散函数的幅值与形态.因此,对点扩散函数进行了高通滤波,去除低频的背景噪声.图7c、d分别表示噪声压制后拖缆和OBN资料对应的点扩散函数.

图7 点扩散函数(a) 拖缆资料的点扩散函数; (b) 接收间距为0.4 km的OBN资料的点扩散函数; (c) 去噪后拖缆资料的点扩散函数; (d) 去噪后OBN资料的点扩散函数.Fig.7 Point spread functions(a) Point spread functions of the towed-streamer seismic data; (b) Point spread functions of the OBN data with an interval of 0.4 km; (c) Denoised point spread functions of the towed-streamer seismic data; (d) Denoised point spread functions of the OBN data.
图8是两种资料联合偏移与单一资料偏移结果的对比.其中,图8a是理论垂直反射率模型,采用式(15)进行计算(朱光,2016;方修政等,2018):
(15)

图8 不同资料LSRTM成像剖面对比(a) 理论垂直反射率模型;其中黑线代表图9中成像曲线的位置; (b) 仅使用拖缆地震资料; (c) 仅使用接收间距为0.4 km的OBN资料; (d) 联合使用拖缆和接收间距为0.4 km的OBN资料; (e) 联合使用拖缆和接收间距为0.8 km的OBN资料; (f) 联合使用拖缆和接收间距为1.6 km的OBN资料.Fig.8 Comparison of LSRTM images using different seismic data(a) Theoretical vertical reflectivity model;The black line indicates the location of image curves shown in Fig.9; (b) Using only the towed-streamer seismic data; (c) Using only the OBN data with and interval of 0.4 km; (d) Using the towed-streamer and OBN data with an interval of 0.4 km; (e) Using the towed-streamer and OBN data with an interval of 0.8 km; (f) Using the towed-streamer and OBN data with an interval of 1.6 km.
其中,m表示反射率,x表示空间坐标,δv表示偏移速度与理论速度之差,v0表示偏移速度.图8b、c分别是仅使用拖缆地震记录和仅使用接收间距为0.4 km的OBN记录的LSRTM成像剖面,图8d、e、f分别是拖缆资料与接收间距为0.4 km、0.8 km和1.6 km的OBN资料联合LSRTM成像剖面.对比图8b和图5a可以看出,拖缆资料LSRTM成像剖面对中深部大角度倾斜界面成像仍然不清楚.对比图8c和图6a可以看出,使用OBN资料LSRTM成像剖面的中深部同相轴的振幅得到了相对的增强.然而,浅部的偏移噪声整体上仍然非常明显.
对比单一地震资料(图8b、c)和两种资料(图8d)联合后的LSRTM成像剖面可以看出,联合偏移成像剖面中,浅部地层的成像质量与拖缆资料偏移成像剖面的质量相当,深部地层的成像质量与OBN资料偏移成像的成像质量相当.对于模型中部高陡地层和断层,联合成像剖面同相轴的连续性和清晰度高于仅使用拖缆资料的成像剖面,其噪声弱于仅使用OBN资料的成像剖面.
对比图8e和图6b可以看出,仅使用OBN资料逆时偏移成像剖面中存在明显的偏移噪声,联合使用两种资料对偏移噪声有着很好地压制效果,其LSRTM成像剖面中几乎看不到明显的偏移噪声.对比图8e、f可以发现,当OBN间距由0.8 km增加到1.6 km后,虽然LSRTM成像剖面中可以看到较弱的偏移噪声,但是高陡地层和断层的成像质量几乎相当.这表明联合偏移成像对稀疏的OBN资料逆时偏移成像噪声有着很好地压制效果.
综上所述,拖缆与OBN资料联合成像整体上优于单一资料成像,可以得到更好的从浅到深的偏移成像效果.
图9是X=16.25 km处(图8a中黑线)OBN资料的RTM、LSRTM成像曲线和理论反射率曲线及其频谱.RTM成像值(图9c)在浅部(Z<2 km)相对较大,而在中深部相对较小.相比于RTM成像值,LSRTM在深部的成像值(图9e)相对更大.在Z=3.35 km和5.14 km左右,理论反射率曲线(图9a)具有一个明显的波谷,RTM成像曲线在对应位置的波动非常微弱,而LSRTM成像曲线在对应位置具有一个明显的波谷.然而,在Z=4 km左右,理论反射率曲线存在一个明显的波谷,而RTM成像曲线和LSRTM成像曲线对其均没有明显的反映.这主要是由于该深度处地层倾角极大,RTM成像值非常小,如图9c所示.图9b、d、f分别是理论反射率曲线、RTM成像曲线和LSRTM成像曲线的波数谱.RTM成像曲线和理论反射率曲线的波数谱的相关系数为0.72,而LSRTM成像曲线和理论反射率曲线的波数谱的相关系数为0.81.这表明LSRTM成像曲线与理论反射率曲线更接近.

图9 X=16.25 km(图8a中黑线)处的成像曲线及其波数谱(a) 理论反射率曲线; (b)(a) 所示反射率曲线的波数谱; (c) OBN间距0.4 km时逆时偏移成像值; (d)(c) 所示成像值曲线的波数谱; (e) OBN间距0.4 km时最小二乘逆时偏移成像值; (f)(e) 所示成像值曲线的波数谱.Fig.9 Image curves and their corresponding wave-number spectrums at X=16.25 km indicated by the black line in Fig.8a(a) Theoretical vertical reflectivity curve; (b) The wave-number spectrum of the curve in (a); (c) The RTM image curve of the OBN data with an interval of 0.4 km; (d) The wave-number spectrum of the curve in (c); (e) The LSRTM image curve of the OBN data with an interval of 0.4 km; (f) The wave-number spectrum of the curve in (e).
4 结论
受限于拖缆的长度,海洋拖缆地震资料对中深部高陡构造的偏移成像质量较差,甚至难以成像.稀疏OBN资料对深部和高陡构造成像效果较好,但在中浅部引入偏移噪声.OBN间距越大,偏移噪声越严重.本文提出了一种拖缆与OBN资料联合成像域LSRTM方法,其中,在成像域通过计算点扩散函数来估计Hessian矩阵,避免了常规数据域LSRTM通过多次偏移和反偏移来估计Hessian矩阵极其耗时的缺点.理论模型测试表明,该方法把拖缆资料与OBN资料有机地融合在一起,发挥了这两种资料优势互补的作用,能够获得比仅使用单一资料更好的偏移成像效果,是深部复杂构造成像的有效方法.
由于缺乏同一测线的拖缆和OBN实际资料,本文仅使用模型的合成资料进行实验和分析.对于实测资料还存在各种噪声的影响及压制等问题,需要进一步研究.
