基于Adams的焊接机械手的轨迹规划运动仿真

陆青松，汪 洋

(安徽城市管理职业学院 轨道交通学院,安徽 合肥 230011)

0 前言

随着社会的发展和科技的进步，作业分工也越发明晰，由于特殊的工况要求，传统的生产作业方式逐渐被自动化设备所代替[1-3]。其中具有代表性的为焊接作业，其具有重复性高、危险性强、劳动强度大等特点，同时对焊接的可靠性也有较强的技术要求[4-6]。这种环境下人们渴望一种自动化程度更高的机械作业方式，并能够代替传统的人工焊接作业，以获得优质的焊接质量及更高的生产效率，焊接机械手正是在这种环境下应运而生[7-9]。

针对某生产线中对钣金件的焊接作业及工况环境要求，设计出了一款五自由度的焊接机械手，以代替传统的人工焊接作业方式。并基于萨哈D-H坐标法，建立焊接机械手的运动学方程，同时利用Admas软件完成对机械手焊接路径规划，并对仿真结果进行了理论校核，验证了设计的合理性，为后续多自由度机械手的设计提供了重要的参考价值。

1 焊接机械手设计

1.1 设计方案

文中主要针对生产作业中钣金件的焊接设计，由于作业空间有限，要求机械手具有一定的灵活性，适应在不同工况下的作业需求，同时为了提高工作效率可以连续针对两组不同工位的工件进行焊接作业。结合实际作业及成本需求，文中借鉴传统的多自由度的机械手的设计方案，将焊接机械手设计为五自由度，底座借助伺服电机和涡轮蜗杆配合的传动方案使其具有旋转功能以适用不同的工况需求，其他部件采用涡轮蜗杆及齿轮传动相结合的设计方案，保证各个关节能够灵活转动。具体如下图所示：

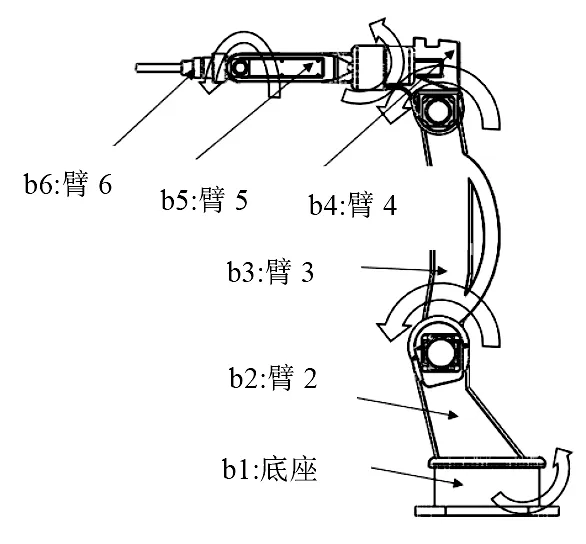
图1 设计方案图

1.2 工况要求

结合实际工况，要求焊接机械手能够连续焊接两个不同的工位，两个工位之间角位差为90度。同时为保证焊接过程中避免碰触大工件，需要保证焊接头和焊件工件之间保证300 mm的安全距离，焊接长度为800 mm。

2 建立运动学方程

2.1 萨哈D-H参数数学模型建立

目前针对机械手的运动学方程的建立，主流方法主要采用标准型D-H坐标法、改进型D-H坐标法和萨哈D-H坐标法，其中萨哈D-H坐标法是利用前一个坐标变换矩阵的参数表示下一个坐标系的位置和姿态，方便用户理解记忆和对机械臂进行控制程序校核，受到众多设计者的青睐[10-12]。文中主要采用萨哈D-H坐标法针对机械臂的运动学方程进行分析。

结合上述模型和萨哈D-H坐标法的特点，建立其动力学分析模型。其中为方便后期调用数据，文中以机械臂末端的焊接执行点的坐标建立坐标系x6y6z6。其余坐标点均建立在各自的旋转轴线上，具体如下图2所示：

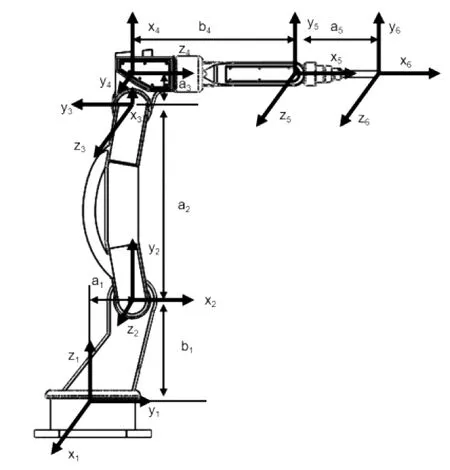
图2 萨哈D-H坐标图

结合上图及模型的具体尺寸数据建立萨哈D-H参数如表1所示：

表1 焊接机械手萨哈D-H参数

2.2 运动学方程建立

结合图2所示，其相邻两个坐标系之间通过4次坐标转换，即坐标系k沿zk方向平移bk使其与xk+1轴相交，坐标系k的xk轴绕zk转动，使其与xk+1轴共线，坐标系k沿xk+1平移，使其两坐标系原点重合和坐标系k的zk轴绕xk+1转动，使其与zk+1轴重合。即如下式所示，表示坐标系k+1经过4次坐标变换后，使其与坐标系k重合[13-14]。

(1)

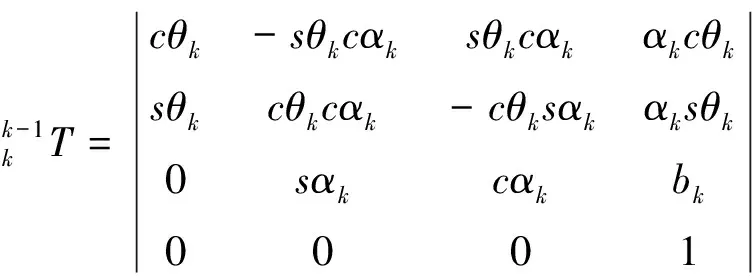
(2)

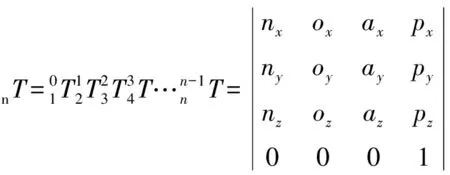
(3)

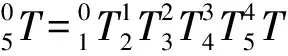
(4)

利用Matlab计算从而得到坐标系x6y6z6相对坐标系x1y1z1对应的Px、Py、Pz的值分别为：

分别为：

PX=160*cos(θ1)+...-139*cos(θ1)*sin(θ2)*sin(θ3)

(5)

PY=160*sin(θ1)-...+(1303*cos(θ3)*sin(θ1)*sin(θ2))/2

(6)

PZ=783*sin(θ2)-.....+cos(θ3)*sin(θ2)+400

(7)

其中θ1、θ2、θ3对应的初始值分别为π/2、π/2、0。

3 Adams运动学仿真

文中主要借助Adams软件对焊接机械手进行运动学仿真，以验证设计的合理性。将机械手的三维模型保存为Adams识别的三维通用格式.x_t格式，以便导入Adams中进行仿真处理[15]。并将图2中x1y1z1坐标移动至Adams坐标系中坐标原点的位置，同时将模型进行适当的旋转处理使其x1y1z1的各轴方向与Adams中系统坐标各对应轴系的方向一致。

三维模型导入Adams中后，结合三维模型各轴之间的运动关系，分别在各关键之间建立旋转副，同时其各个关节的旋转副的坐标位置和上图中2中的坐标位置相对应。同时，在机械手的末端建立尾端坐标系x6y6z6，并给予各关节相应的驱动，其驱动函数如下所示：

对应图2中x1y1z1的y方向的驱动为：

step(time,0,0,1,300)+step(time,3,0,4,-300)+step(time,5,0,6,300)+step(time,8,0,9,-300)

对应图2中x1y1z1的z方向的驱动为：

step(time,1,0,3,-800)+step(time,6,0,8,800)

其余移动方向及转动方向的驱动均设为0。仿真时间为9秒，步数为900步，结束后分别调取坐标系x2y2z2、x3y3z3和x5y5z5所在关节旋转坐标系所在的位置的角速度运动曲线并将其转化为样条驱动曲线。

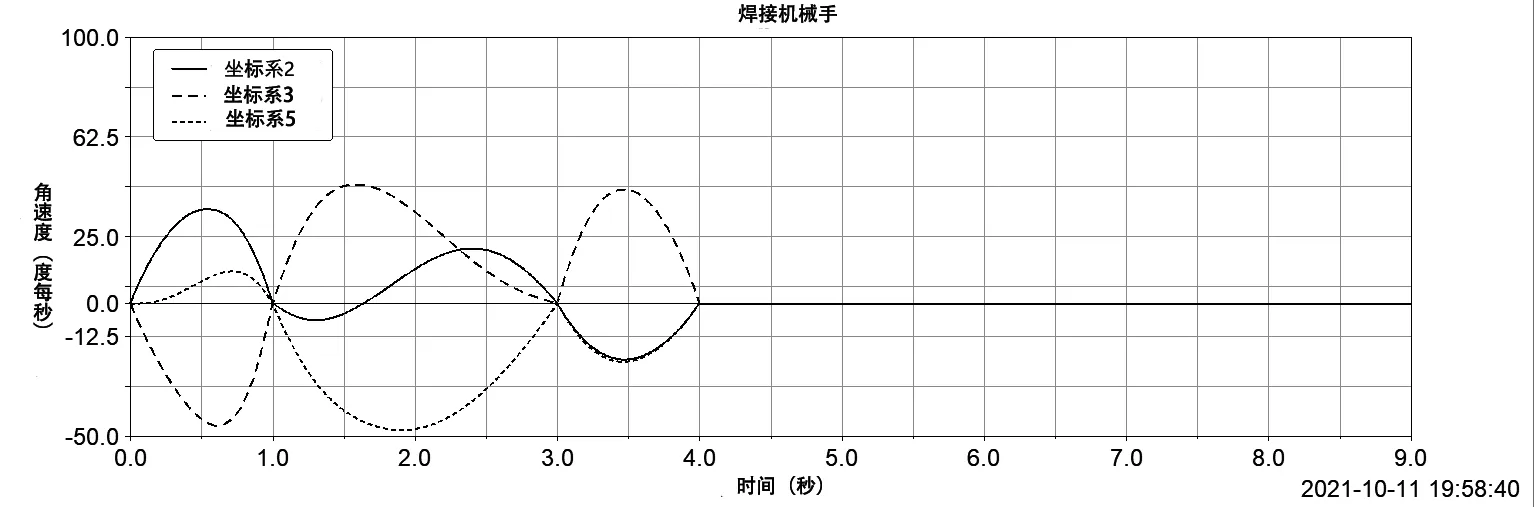
图3 关节2、3、5的旋角速度

上述仿真结束后，分别对图2中对应关节坐标系对应的转动副添加驱动，如下表2所示：

表2 各关节驱动函数

设置完毕后在仿真界面中，将仿真时间设置为9秒，步数为900步对模型进行再次仿真处理，仿真结束后，利用Admas提供点的轨迹捕捉功能，将末端点所在的位置x6y6z6的点在系统坐标系中的运动轨迹调出，如下图4所示。

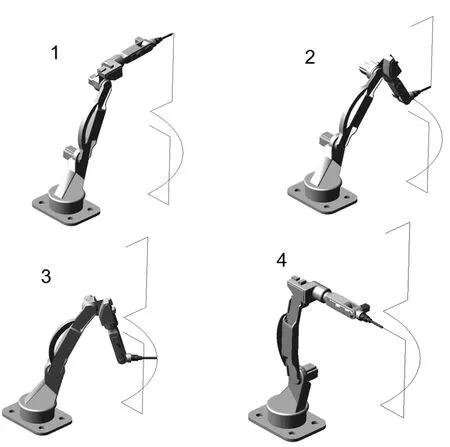
图4 末端点的运动轨迹图

同时在Adams后处理中调取末端点相对系统坐标系，即图2中x1y1z1的位移曲线如下图5所示。

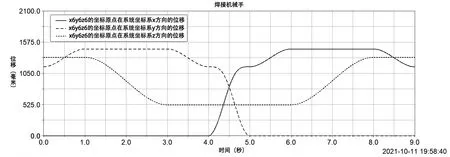
图5 末端点的位移

利用后处理中的数据捕捉功能，提取仿真结束时x6y6z6相对于x1y1z1的坐标值为(1 162,0,1 322)。

为验证其设计理论的合理性，利用Admas的测量功能分别测得关节1～5处个转动副的转动角度，如下图6所示。

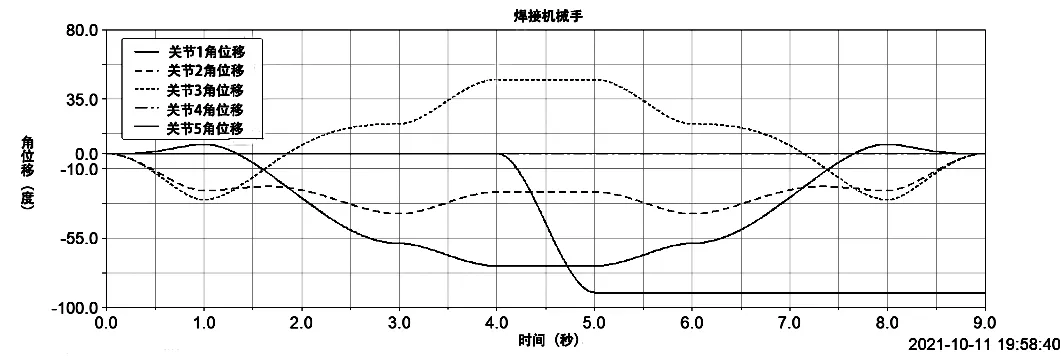
图6 各关节处转动的角位移

由图6中可以看出，各个关节中只有关节1处的角度转动了-π/2，其余转动角度相对初始位置均为零，即表1中只有θ1由原来π/2转动至0度，其余角度均为初始角度，没有发生变化。因此将θ1为0、θ2为π/2、θ3为0、θ4为π/2、θ5为0分别代入公式5、6、7中，得到末端点的终点运动坐标相对坐标系x1y1z1的值为(1 162.023 4，0，1 322.022 4)。仿真得到的数据为(1 162,0,1 322)与理论值相接近，且误差在允许的范围内。从而验证了焊接机械手的运动轨迹满足设计要求及理论要求，验证了设计的合理性。

4 结论

文章设计出了焊接机械手的三维模型，基于萨哈D-H坐标法对焊接机械手的运动学方程进行了搭建，完成了对机械手的运动理论分析。同时借助Adams软件完成了对焊接机械手特定工况下轨迹规划和运动学分析，并对仿真的结果进行了理论验证，进一步验证了焊接机械手结构设计的合理性，可以为后期对机械手的研究提供设计参考和依据。