弹引系统螺纹传递冲击荷载数值仿真方法

邸跃红

（西安机电信息技术研究所，陕西 西安 710065）

螺纹连接不仅具有较高可靠性，而且具有结构简单、装拆方便等优点，因而被广泛应用于各种连接结构中，侵彻弹的弹体与引信之间一般采用螺纹进行连接，螺纹在连接两部分的同时也将冲击荷载由弹体传递至引信。为了更准确地确定引信上的过载信号，就需要对螺纹传递冲击荷载的特性进行研究。

Bahai[1]基于二维轴对称模型，分析了螺纹连接在受轴向力和弯矩作用下的应力集中程度；Yuan等[2]基于二维模型仿真计算了螺纹连接在不同预紧速度和不同预紧力下的温度场及应力场分布；Fu[3]建立二维模型，对弹丸内螺纹连接部分的应力分布进行了仿真分析，并校验其强度；况雨春等[4]对单台肩锥螺纹在紧扣力矩下的力学特征进行研究，并对锥度等影响因素进行了参数化分析；狄勤丰等[5]采用有限元方法研究了双台肩锥螺纹在紧扣力矩及拉伸荷载作用下的力学特征；A.R.等[6]三维设置不同载荷情况，对锥螺纹最大应力集中位置及系数进行研究；Chen等[7]对螺纹连接进行了三维有限元分析，研究了螺旋和摩擦对各螺纹载荷分布的影响；鄢阿敏等[8]引入薄层单元模拟螺纹连接，并对其模态频率进行了仿真分析；殷瑱等[9]研究了引信内腔封口处螺纹连接的受力情况，并研究了螺距对其的影响。

本研究建立了三维带螺旋升角的螺纹连接受力数值计算模型，采用Yamamoto螺牙接触力分布理论对仿真模型的合理性进行验证。在此基础上对模型施加冲击载荷，对比激励曲线与响应曲线，得到螺纹传递冲击荷载的特性。

1 螺纹连接力学模型

1.1 螺纹连接处受力特征

紧扣力矩作用下，公螺纹和母螺纹会在台肩处相互挤压并产生弹性变形。紧扣完成后，紧扣力矩被撤销，便会在二者的接触面上产生回弹力F0，在回弹力的作用下，公螺纹和母螺纹的螺牙紧密贴合并产生接触力F（x），其纵截面上的受力特征如图1所示。

图1 预紧力作用下的受力特征

沿螺牙升角方向对螺纹齿面进行受力分析，其受力特征如图2所示，其中β为螺牙升角，接触力F（x）可分解为齿面法向力σ和切向力τ，其可产生的最大静摩擦力fmax=μσ=μFcosβ，而螺牙升角设计时满足μFcosβ＞Fsinβ，即螺纹齿面可发生摩擦自锁现象，螺纹配合在预紧作用下可达到受力平衡，且幅值较小的外力无法打破这种平衡状态，从而满足预紧要求[10]。

图2 螺旋升角方向的受力特征

1.2 螺牙接触力分布数学模型

如上所述，公螺纹和母螺纹的螺牙紧密贴合并产生接触力F（x），虽然各层螺牙尺寸相等，但各齿面上接触力并不相等，海内外学者对螺牙接触力计算进行了大量研究，其中Yamamoto的螺牙接触力分布理论[11]应用最为广泛。该理论先将螺牙等效为平面应变悬臂梁，将法向接触力和切向接触力（即摩擦力）的合力P沿水平方向和垂直方向分解，分别考虑两个方向的分力对螺牙变形的影响，得到了接触力作用下内螺纹和外螺纹的变形系数；再沿螺纹轴向选取坐标为x到x+dx之间的部分，考虑该部分的受力平衡，并考虑螺旋升角的影响，最终得到了各层螺牙上接触力系数与其位置x的函数关系，详见参考文献[11]。

2 螺纹连接数值仿真模型及其验证

LS-DYNA软件是一款拥有强大功能的动力学仿真软件，其具有强大的显式求解器，可以处理复杂接触条件下的非线性动力学问题，除此之外，其兼有隐式求解能力，可以对预应力及静力回弹等静力学问题进行分析。考虑到既包含复杂条件下的冲击问题，又需要对结构进行静力预紧，故采用LS-DYNA软件进行数值仿真。

2.1 螺纹连接数值仿真模型

考虑了螺旋升角对螺纹连接的影响，忽略了侵彻弹弹体及引信的具体构型，建立了螺纹连接处的三维精细模型，母螺纹、公螺纹网格模型分别如图3、图4所示，母螺纹表示侵彻弹体上的螺纹盲孔，公螺纹表示引信的旋入部分，其牙型采用公制三角形螺纹M72×4。二者均采用体单元划分网格，在螺牙接触部分划分较细的网格，并在求解时将其设置为二阶单元以提高计算精度，其余区域划分为尺寸略大的六面体网格并设置为一阶单元以提高计算效率。其中螺纹配合处的纵截面剖视图如图5所示。

图3 母螺纹模型及网格

图4 公螺纹模型及网格

图5 螺纹配合处剖视图

螺纹连接处的材料为Q235钢，由于该区域承受冲击荷载，需考虑高应变率下的材料性能，故选用该材料的Johnson-Cook本构模型[12]，材料相关参数见表1。

表1 Q235钢Johnson-Cook模型参数

2.2 预紧力仿真及其正确性验证

当紧扣力矩作用时，公螺纹和母螺纹会在台肩处相互挤压并产生弹性变形，紧扣力矩撤销后，便会在二者的接触面上产生回弹力，在回弹力的作用下，公螺纹和母螺纹的螺牙紧密贴合并具有一定的接触力，此时由于螺纹齿面的摩擦自锁现象，螺纹配合不会自动旋出，且较小的外力也不会打破此处的受力平衡，从而达到预紧作用。为模拟这种预紧机理，本研究在公螺纹的台肩处施加预紧力，其位置及方向如图6所示，该预紧力通过LS-DYNA软件的*Initial关键字施加，即将预紧后的应力应变计算结果作为后续冲击动力学分析的初始条件。

图6 预紧力施加示意图

定义接触力系数为第n层螺牙与第1层螺牙接触力的比值，其中，最接近预紧平面的螺牙为1号螺牙，自右向左（远离预紧平面）依次为2，3，4……号螺牙，将预紧后螺纹齿面接触力系数的仿真值与Yamamoto螺牙接触力分布理论进行对比，对比曲线如图7所示，由于两曲线吻合程度较好，表明螺纹配合计算模型的合理性。

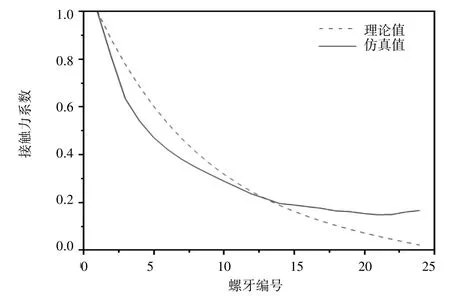
图7 仿真值与理论值对比

3 螺纹传递轴向冲击载荷仿真结果

为使计算结果更具有现实意义，认为母螺纹位于弹体上，公螺纹位于引信体上。取侵彻弹过载加速度曲线作为激励输入母螺纹的左端面，该激励波形如图8所示。

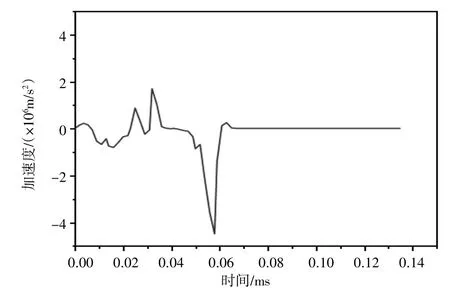
图8 侵彻弹加速度激励曲线

3.1 激励与响应对比分析

用公螺纹表示引信的旋入部分，故主要观察公螺纹各点的加速度响应，而螺纹各点由于所处位置不同，其响应也具有较大的差别，故取公螺纹不同位置的4个点（点2-5），如图9所示，分别与点1处激励进行对比。

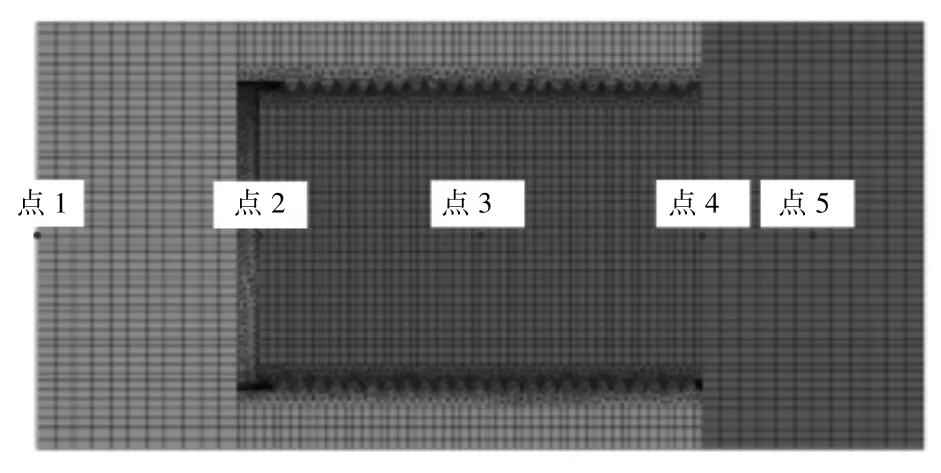
图9 激励点与响应点位置示意图

为使响应曲线频率与幅值与激励曲线对比更加明显，将响应曲线进行移波处理，得到响应与激励的对比曲线如图10～图13所示。

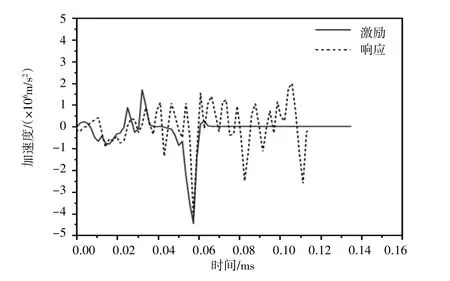
图10 点2处响应与激励对比

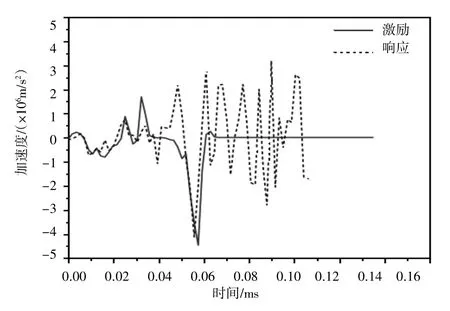
图11 点3处响应与激励对比

图13 点5处响应与激励对比

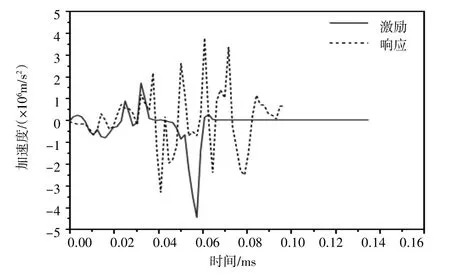
图12 点4处响应与激励对比

图10～图13对比表明：冲击荷载传递时螺牙具有一定的缓冲作用，得到响应曲线的幅值略小于原始波形；应力波传递时产生弥散，且螺牙间发生碰撞，故响应波形较激励波形波动性更大，且与激励波形吻合程度较低，距离激励越远该现象越明显。

3.2 螺纹连接建模方法对比分析

弹丸侵彻仿真一般较为复杂，为了节约计算成本，会对模型进行简化处理，其一般处理方式包括：不考虑弹引系统的螺纹连接将其视为一个整体，即建模时将模型建为一体化模型；采用TIE连接或粘接等方式连接弹引系统。为了分析这些简化处理方式所得结果的偏差，建立了相应的简化模型，输入相同激励，取相同点位进行对比分析，各点响应曲线对比如图14～图17所示。

图14 点2处响应与激励对比

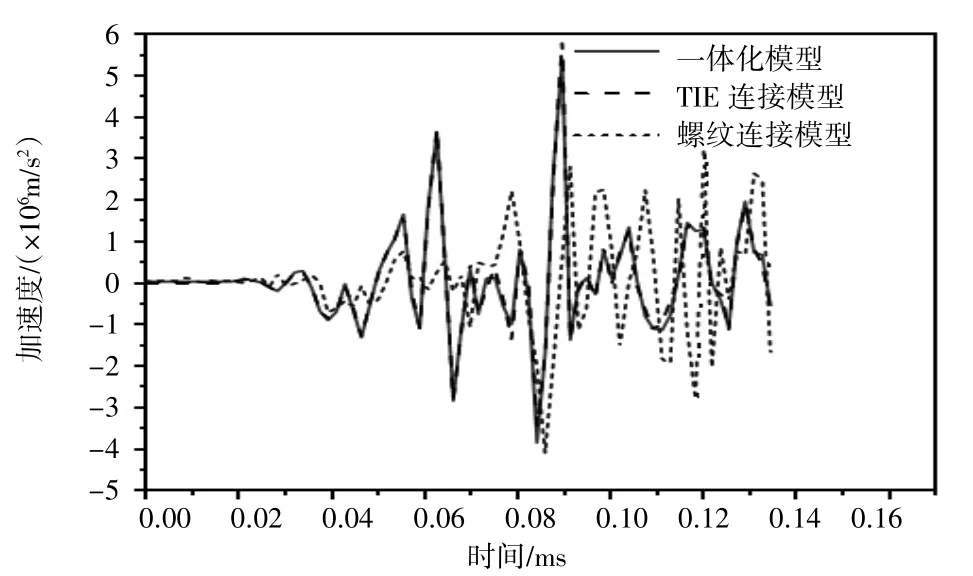
图15 点3处响应与激励对比

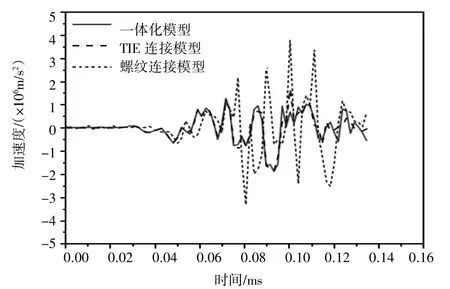
图16 点4处响应与激励对比

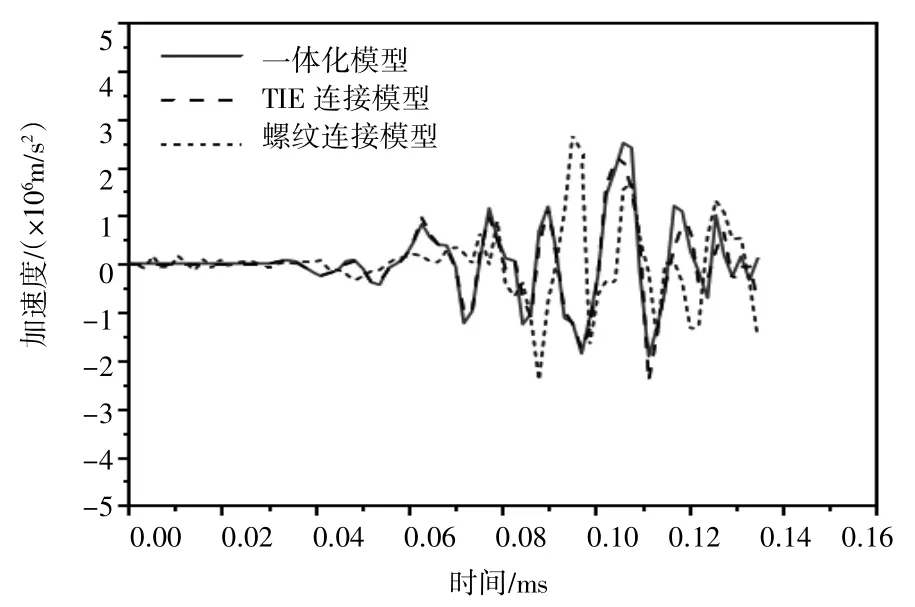
图17 点5处响应与激励对比

图14～图17对比表明，一体化模型与TIE连接模型所得响应曲线吻合程度较高，且与激励波形较为吻合，说明这两种简化方式效果较为接近，但二者与真实螺纹连接所得响应曲线差异明显，具体表现为：响应初始阶段螺纹连接具有一定的缓冲作用，所得响应的幅值略小于其他两种方式；后续由于螺牙间发生碰撞，产生了新的应力波，与原始波形叠加后，其波形与幅值都发生了不同程度的变化。

4 结论

建立的带螺旋升角的螺纹三维精细有限元计算模型，并用Yamamoto螺牙接触力分布理论解对计算模型的合理性进行验证，得到的结论如下：

（1）螺纹传递冲击荷载时具有如下特性：螺牙具有一定的缓冲吸能作用，会使响应曲线的幅值略小于激励，冲击作用下螺牙间会发生碰撞，使响应曲线波形更复杂，具有更大的波动性。

（2）数值仿真结果表明，一体化模型与TIE连接模型结构更加简单，这些简化方式虽然可减少计算成本，但在螺纹附近处得到的结果较真实螺纹连接相比具有明显误差。