开口截面波折钢腹板组合梁抗扭性能研究

张 冀

(广西交通投资集团南宁高速公路运营有限公司，广西 南宁 530022)

0 引言

国内外对波折钢腹板组合梁抗扭性能的研究主要集中于抗扭刚度计算公式推导、抗扭承载力计算公式推导、抗扭设计方法、约束扭转与畸变应力分析、横隔板合理间距估算公式、腹板波折形状对抗扭性能的影响等。Y.L.Mo等[1]基于软化混凝土的平衡方程，推导出了此类桥的抗扭承载力的计算公式。李宏江等[2]通过一片试验梁，验证了其推导得出的波折钢腹板组合箱梁畸变和约束扭转计算公式。Y.L.Mo等[3]基于之前的研究提出了波折钢腹板组合箱梁的抗扭设计方法。王圣保等[4]通过试验和有限元分析，得出波折钢腹板上由约束扭转及畸变产生的附加剪应力约为剪应力的1.5倍。丁勇、江克斌等[5]以扭转理论和固定角软化桁架模型为基础，推导了纯扭作用下波折钢腹板组合箱梁的抗扭承载力计算模型。马磊[6]应用薄壁结构的分析理论，通过试验验证了单箱多室波折钢腹板组合箱梁的扭转微分方程和畸变微分方程的适用性。唐杨等[7]通过建立波折钢腹板组合梁的模型，得出在折角位置增加横隔板可以有效降低箱梁最大扭转正应力的结果。

为了进一步探索波折钢腹板组合梁的抗扭性能，本文进行了多参数变化有限元分析。

1 有限元模型建立

1.1 计算模型参数

波折钢腹板曲线T梁模型由腹板为波折钢板的工字钢和混凝土顶板组成，模型梁沿着中线展开后，全长4 600 mm，计算跨径为4 300 mm，边界条件为简支。组合梁高500 mm，其中工字钢主梁高度为420 mm，钢主梁腹板高度为396 mm，厚度为4 mm；上下翼缘厚度均为12 mm，宽度均为200 mm。混凝土顶板宽度为600 mm，厚度为80 mm。波折腹板曲线T梁几何尺寸及加载方式如图1所示。

(a)立面图

1.2 有限元模型

使用有限元软件建立8根波折钢腹板曲线T梁，研究曲率半径从10 m变化到正无穷(直梁)的过程中模型梁在双点荷载的作用下极限承载力的变化情况以及弹性阶段跨中截面扭转角的变化情况。对影响不同曲率半径下模型梁扭转性能的主要因素进行了变参数分析，变化的参数有：曲率半径、腹板类型、腹板高度。

本文有限元模型网格的大小控制在30 mm以下，同时考虑到桥面板厚度方向的尺寸较小，实际桥面板厚度方向可能存在较大的应力梯度，因此在桥面板厚度方向至少划分为3层网格。模型梁整体网格划分如图2所示。

图2 模型梁整体网格划分示意图

2 曲率半径对扭转性能的影响

以腹板类型为“135+155”(135为波折钢腹板的斜线段水平投影长度，155为波折腹板的直线段长度)的波折钢腹板直线单梁为基础，分别改变模型梁的曲率半径，形成曲率半径分别为R=∞(直梁)、R=200 m、R=150 m、R=100 m、R=75 m、R=50 m、R=25 m和R=10 m的8根腹板类型为“135+155”的波折钢腹板曲线单梁，对比不同曲率半径对波折钢腹板曲线单梁抗扭性能的影响。各模型仅变化曲率半径，其余构造尺寸不改变，具体参数及属性如表1所示。

表1 试验梁参数表

按照第二节所示施加两点荷载，使用垫块分布应力，具体位置按照“135+155”型波折钢腹板曲线单梁来定，其他腹板类型的单梁为控制变量的单一性，采用与之相同的加载位置。

如图3所示，随着曲率半径的增大，波折钢腹板组合梁的扭转效应相对变小，极限荷载也随之加大，半径≥50 m的波折钢腹板曲线T梁的加载过程可以大致地分为弹性工作阶段和弹塑性工作阶段，而且屈服点位置基本一致；而半径<50 m的梁在加载过程中受扭转效应的影响在弹性阶段就发生了破坏。弹塑性工作阶段组合梁的挠度随荷载增长均匀增加，结构进入弹塑性工作阶段后，组合梁的挠度迅速增加。

图3 “135+155”型模型梁荷载位移曲线图

双点加载工况下不同曲率半径的模型梁在单个点的荷载大小为2 t、6 t和14 t这三个工况下，跨中截面混凝土顶板及钢主梁下翼缘的扭转角变化情况如图4所示，从图形整体变化趋势上可以看出，随着模型梁曲率半径的增大，曲线梁受扭转效应的影响逐渐变小，跨中截面混凝土顶板及钢主梁下翼缘在不同荷载等级下的扭转角也逐渐变小。当曲率半径>100 m之后模型梁跨中截面混凝土顶板及钢主梁下翼缘的扭转角逐渐趋向一个定值，而且荷载等级越小这一趋势越明显。此外，在不同荷载等级下曲率半径越小，扭转效应越明显，模型梁跨中扭转角的变化越显著。这些结论说明曲率半径的存在会影响梁的扭转性能，而且曲率半径越小影响越大。此外，在不同荷载等级下模型梁跨中截面混凝土顶板及钢主梁下翼缘扭转角的变化趋势基本保持一致，但在同一荷载下混凝土顶板的扭转角比钢主梁下翼缘的扭转角要大，而且荷载越大两者的差别越大。这说明波折钢腹板和钢主梁下翼缘在扭转过程中存在畸变变形。

图4 跨中扭转角随曲率半径的变化曲线图

如图5、图6所示分别为曲率半径为75 m和150 m的两根模型梁在极限荷载状态下的混凝土顶板挠度及混凝土顶板上下表面应力云图。

由图5两张不同曲率半径的模型梁在极限荷载下桥面板的位移云图，可以发现由于曲率引入的扭转效应的存在，这两根梁在极限荷载下都是曲线外侧的挠度较曲线内侧的挠度大。而且曲率半径小的模型梁桥面板位移云图深色区域向曲线外侧偏移情况较曲率半径大的模型梁更为严重，从混凝土上下表面应力云图可以发现同样的规律。

3 腹板类型对扭转性能的影响

以7根不同曲率半径的“135+155”型波折钢腹板曲线单梁TL2～TL8为基础，改变波折钢腹板参数及单梁线型，形成不同曲率半径的“100+125”型波折钢腹板曲线单梁。对比不同曲率半径和不同腹板类型对波折钢腹板曲线单梁抗扭性能的影响。各模型仅变化腹板类型，其余构造尺寸不改变，模型梁具体参数如表2所示。

表2 试验梁参数表

不同腹板类型的两组模型梁在不同曲率半径下的极限荷载分布规律如图7所示，可以发现两种不同腹板高度的模型梁在曲率半径≤50 m之前，随着曲率半径的增大，由曲率引入的扭转效应快速减小，单点极限荷载迅速增大；曲率半径从50 m变为75 m期间，两种不同腹板高度的模型梁的单点极限承载力均以较小的幅度有所增加；当曲率半径达到75 m之后，由曲率引入的扭转效应不再明显，两类梁的单点极限承载力基本保持稳定。两种腹板类型的波折钢腹板曲线梁在相同曲率半径下的单点极限荷载相差较小，曲率半径为50 m处两者相差最大，腹板类型不同的两根梁极限荷载的差值为“135+155”型模型梁的13.4%。从整体趋势上来看，在每个不同的曲率半径下“135+155”型模型梁的极限承载力都要较“100+125”型模型梁大，这说明“135+155”型模梁的抵抗扭转的性能较“100+125”型模型梁稍好。见图8。

(a)R=75 m顶板极限荷载下梁高方向

(a)R=75 m顶板极限荷载下上表面

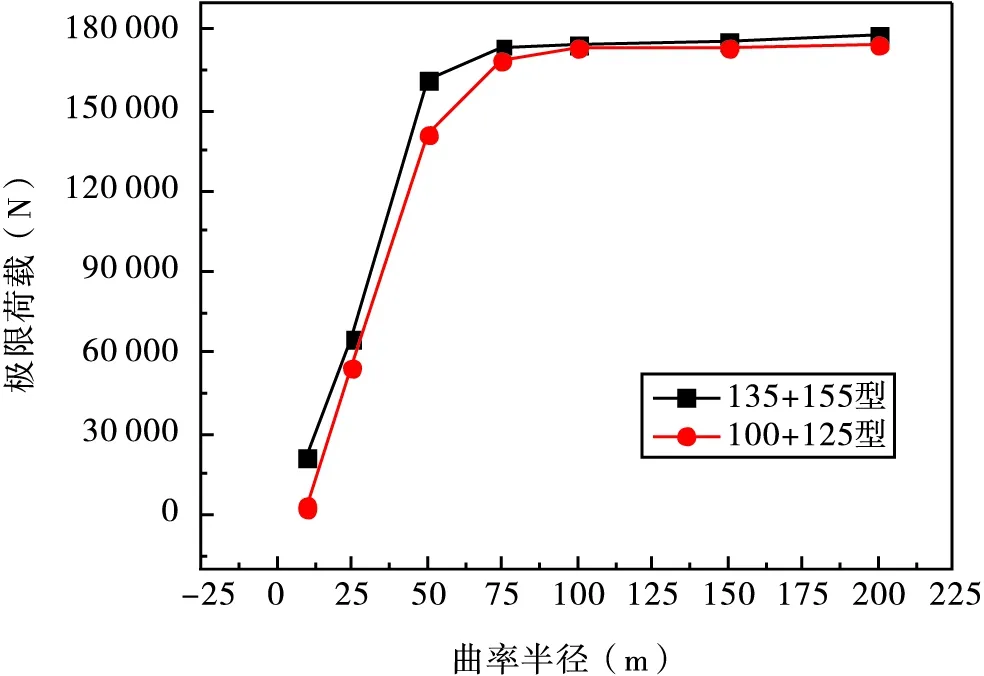
图7 不同腹板类型的模型梁在不同曲率半径下的极限荷载曲线图

图8 不同腹板类型的模型梁在不同弹性荷载下跨中截面曲率半径-扭转角曲线图

4 腹板高度对扭转性能的影响

为研究不同腹板高度对波折钢腹板曲线T梁桥扭转性能的影响，对腹板高度为396 mm的7根模型梁进行变腹板高度模拟，分别形成7根腹板高度为346 mm和7根腹板高度为446 mm的变参模型梁。不同腹板高度的三组模型梁在不同曲率半径下的极限荷载分布规律如图9所示，可以发现三种不同腹板高度的模型梁在曲率半径≤50 m之前，随着曲率半径的增大单点极限荷载迅速增大，由曲率引入的扭转效应变化也十分明显，曲率半径从50 m变为75 m的过程中，三种不同腹板高度的模型梁的单点极限承载力均以较小的幅度有所增加；当曲率半径达到75 m之后，由曲率引入的扭转效应不再明显，三类梁的单点极限承载力基本保持稳定。

随着曲率半径的增大，不同腹板高度的模型梁的极限荷载也在随之增大，而且从图9可以看出，当曲率半径为10 m和25 m的时候，不同腹板高度的模型梁的极限荷载差别不大；而当曲率半径达到50 m之后，极限荷载明显增大，且腹板高度越高，模型梁截面的抗弯及抗扭能力越强，模型梁能承受的极限荷载越大。当曲率半径为50 m时，腹板高度为446 mm的模型梁的单点极限荷载分别为腹板高度为396 mm和346 mm的模型梁的极限荷载的1.1倍和1.3倍；当曲率半径为200 m时，腹板高度为446 mm的模型梁的单点极限荷载分别为腹板高度为396 mm和346 mm的模型梁的极限荷载的1.2倍和1.4倍。

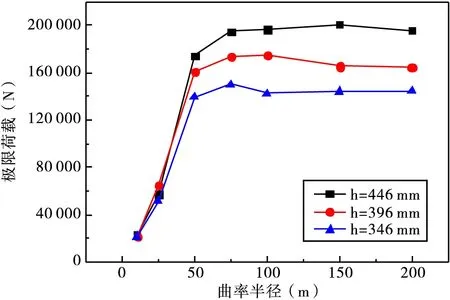
图9 不同腹板高度下曲率半径-极限荷载曲线图

如图10所示为腹板高度分别是346 mm、396 mm、446 mm的三组曲线梁，在荷载分别为2 t、6 t、13 t的三种工况下，混凝土顶板跨中截面扭转角随曲率半径的变化曲线图。从图中可以看出，每种荷载工况下的三组腹板高度不同的曲线梁跨中截面扭转角的变化趋势基本一致，扭转角数值差别不大。从整体变化形式上看，同一荷载和曲率半径下，腹板高度越小，跨中截面的扭转角相对越大。腹板高度越高模型梁截面的抗扭转刚度越大，抵抗扭转的性能越强。

图10 弹性荷载下模型梁曲率半径-扭转角曲线图

5 结语

本文对开口截面波折钢腹板组合曲梁进行了扭转性能有限元变参分析。从变参分析可知，不同腹板类型对模型梁承载力的影响较小，扭转效应更多的是与曲率半径有关。腹板高度对曲线梁极限承载力的影响较大，三组腹板高度不同的模型梁在腹板高度增大的过程中，极限承载力整体上升，而跨中截面扭转角整体变小。在极限荷载工况下，随着曲率半径的增大，模型梁中由曲率引入的扭转效应变得不再明显，波折钢腹板组合梁的极限荷载也随之加大。