L-Q-T坐标下的P波与S波接收函数联合反演
2022-09-30黄思涵董树文贺日政韩宝福
黄思涵 , 董树文 , 贺日政, 韩宝福,周 琦, 吴 蔚 , 牛 潇
1)中国地质科学院, 北京 100037;2)北京大学地球与空间科学学院, 北京 100871;3)南京大学地球科学与工程学院, 江苏南京 210093
P波接收函数对深部结构具有较高的分辨率,因此成为探测地壳及上地幔结构特征的主要技术手段被广泛运用(Vinnik, 1977; Langston, 1979; Ammon, 1991; Yuan et al., 1997; Ligorría and Ammon,1999; Chen et al., 2006; Kind et al., 2012; Yu et al.,2012; He et al., 2014)。然而在P波接收函数波形中,沉积层引起的多次波会压制台站下方Moho面的转换波, 进而影响壳幔结构的重建。
由于稳定克拉通表面的沉积层与其下覆结晶基地之间存在较大波阻抗, 能形成幅值较大的沉积层转换波及后续多次波, 会干扰 Moho面处的转换波信号(Sodoudi et al., 2009; 唐有彩等, 2010;Langston, 2011; Yu et al., 2015)。特别是二者走时接近情况下, 常常会造成广泛使用的 H-κ方法(Zhu and Kanamori, 2000)失效, 因此无法准确地估算地壳厚度和Vp/Vs比值。与P波接收函数相比, S波接收函数因转换波与多次波分别分布初至波的前后,可免受多次波的干扰。S波接收函数中最被关注的震相是在岩石圈与软流圈间界面(LAB)产生的转换波S-LAB-P(下文简写为Slp)。人们较少地运用地壳底部 Moho面产生的转换波 S-Moho-p(下文简写为Smp)。事实上, Smp波也是可靠地获取壳幔内部结构的一个有效信号。为了同时得到Pms和Smp转换波,本文介绍了基于L-Q-T坐标下提取P波和S波接收函数过程, 运用正演模拟讨论了沉积层对P波和S波接收函数的影响, 并通过实例分析具有巨厚沉积层的渭河盆地和河套盆地的两台站, 验证了L-Q-T坐标下P波和S波接收函数联合反演能够有效地压制沉积层多次波干扰, 较为可靠地获取台站下方的壳幔结构特征。通过将共振滤波器方法和P波、S波联合反演的方法运用于渭河盆地和河套盆地内的两个流动台站, 结果表明联合反演方法更具优势, 除能获得界面深度信息, 还能获取速度信息。
1 L-Q-T坐标下的接收函数
接收函数(Receiver Function)是一种利用远震体波在壳幔内部的多种分界面所产生的转换波来探测地球深部不连续界面的方法。通过消除仪器、震源及在传播路径的影响, 获取台站下方壳幔不连续界面的时间序列函数。Vinnik(1977)首次利用了Ps转换波探测到了挪威地下410 km处和660 km处的不连续面, 后该方法被命名为接收函数(Langston,1979)。由远震体波P波和S波所对应的转换波获得的接收函数分别叫做P波接收函数和S波接收函数(图 1)。
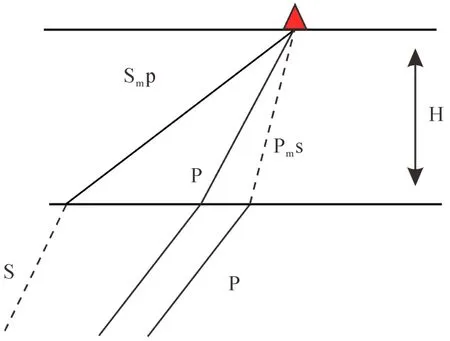
图1 P波、S波接收函数射线路径图(改自 Farra and Vinnik, 2000)Fig.1 Ray path of P-wave and S-wave receiver function(modified from Farra and Vinnik, 2000)
P波接收函数和S波接收函数的提取步骤主要有以下三步: 先通过坐标旋转, 突出转换波的能量;再通过滤波压制噪声; 最后通过时间域或频率域反褶运算(Ammon et al., 1990)去除震源、传播路径和仪器响应, 最后提取到接收函数。
在地震仪中, 人工制作的仪器标定坐标一般为Z(垂直)、N(北向)和E(东向)三道。为了获取高质量的台站下方介质响应, 需要将观测仪器的Z-N-E坐标旋转到地震波传播路径上。因此, 通过坐标旋转, 确保转换波的能量被最大程度恢复。坐标旋转通常有二轴旋转(Z-R-T)和三轴旋转(L-Q-T)两种方式(图2)。
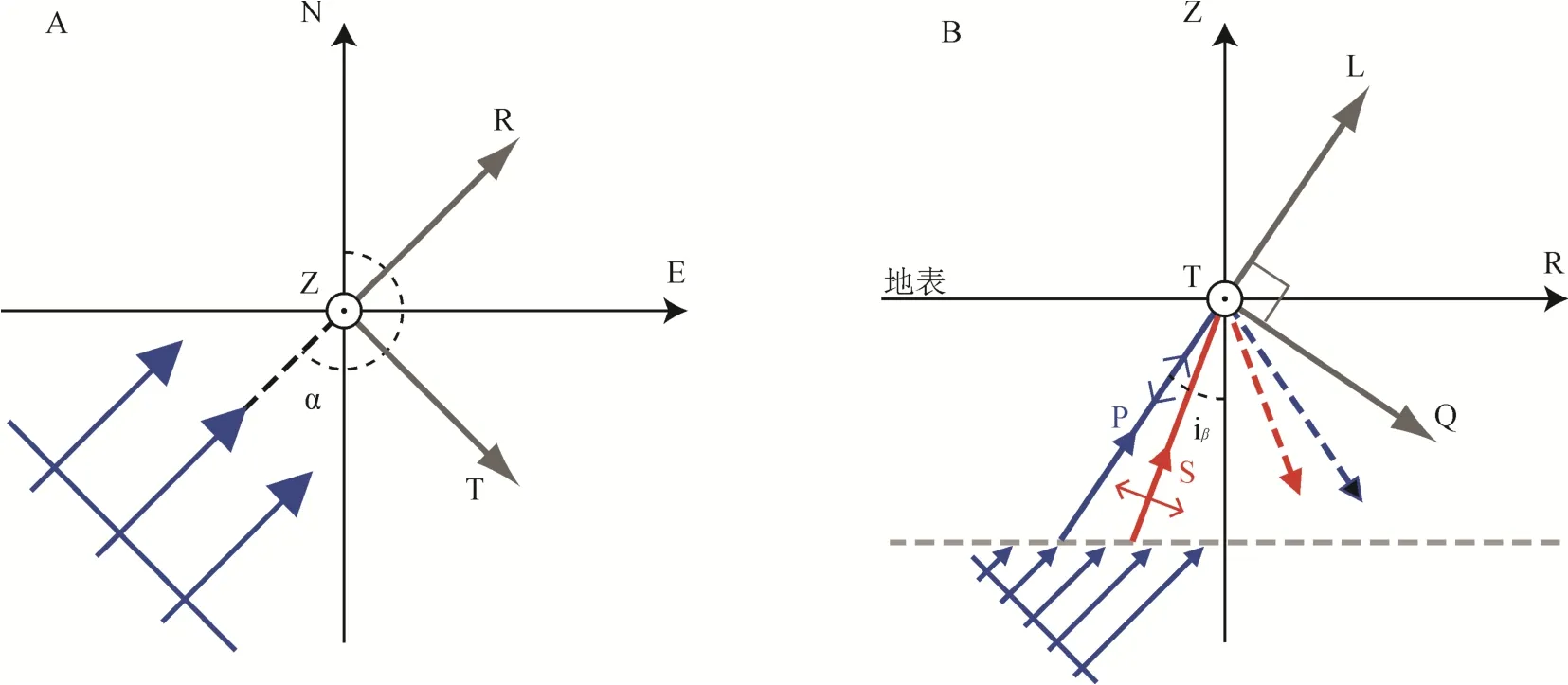
图2 Z-R-T和L-Q-T坐标系下波场分解图(Rondenay, 2009)Fig.2 Wavefield decomposition diagram in Z-R-T and L-Q-T coordinates (Rondenay, 2009)
二轴旋转采用后方位角将地震仪坐标Z-N-E(垂向、北向和东向)的三分量利用公式(1)旋转到Z-R-T(垂向、径向和切向)坐标系, (1)式中α是后方位角。
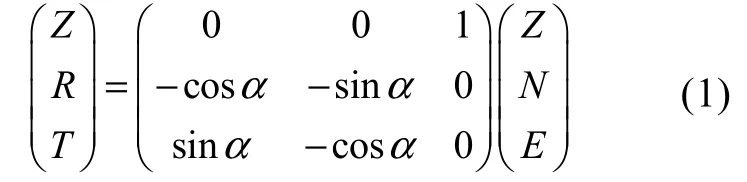
在Z-R-T坐标下, R分量为震源、仪器响应及台站下方地下介质的褶积。通过反褶运算求解出ER的过程, 即为提取接收函数。
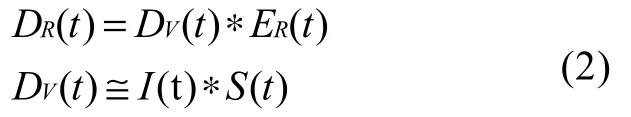
Z-R-T坐标下提取接收函数时, 假设地震仪器记录到的地震波为近垂直入射且地球介质为各向同性, 这样才能确保台站下方的不连续界面产生的转换波能量最大程度地集中于R分量。在实际中, 由于Z-R-T坐标并不是真实的地震波传播路径, 因此经反褶运算得到的R分量接收函数仍存在直达P波幅值远大于转换波能量(Kind et al., 2012), 导致期望来自地下浅部界面所产生的转换波信号会被泄漏的直达P波所压制, 从而无法识别。
为此, 利用公式(1)实施二轴旋转(Z-R-T)后, 再利用 P波入射角(iβ)经公式(3)实施三轴旋转(L-Q-T)。
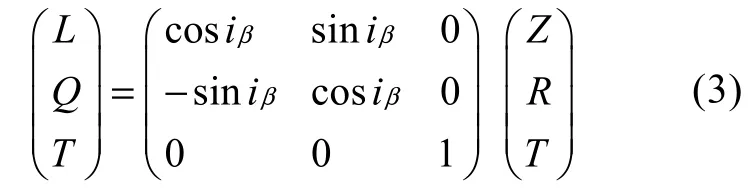
式(3)中 P波入射角(iβ)由 Z-N-E三分量所记录的直达P波到达后数秒时间窗口内的协方差矩阵的特征值决定(Montalbetti and Kanasewich, 1970)。L轴表示直达P波的偏振方向, Q轴表示SV波偏振方向, T轴垂直于L和Q组成的平面, 代表了SH波的偏振方向。存在于L-Q-T坐标系内T轴上的能量可认为是转换 Ps波在传播过程中由横向不均匀的介质或各向异性的介质所产生。这样, 在L-Q-T坐标下经反褶积运算后得到的Q分量即为P波接收函数, T分量可用于分析研究台站下方介质的各向异性(Farra and Vinnik, 2000)。因此, 在L-Q-T坐标下获得的P波与S波接收函数, 理论上在零时刻消除了直达P波和直达S波的能量, 并保留着地下各不连续面的转换波能量, 能较好地分辨地下浅层结构信号。
在L-Q-T坐标下, 在频率域中可用公式(4)提取P波接收函数, 用公式(5)提取S波接收函数。
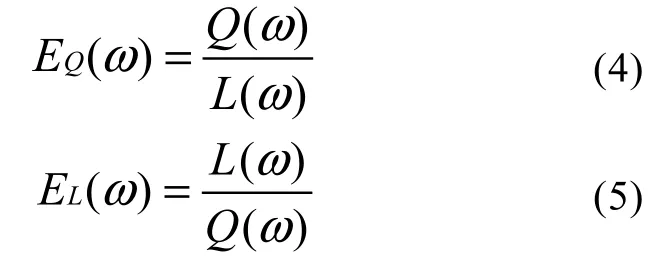
上述两式表明, L-Q-T坐标系下, 反褶积运算后得到的Q分量即为P波接收函数(PRF), L分量为S波接收函数(SRF)。由于频率域的反褶积运算是除法运算, 分母接近零时, 会导致运算不稳定。因此,本文采用时间域 Wiener滤波的反褶积方法提取接收函数(Berkhout, 1977)。
2 不同沉积层厚度对P波接收函数影响
在沉积盆地及其周缘利用P波接收函数进行其下的壳幔结构研究中, 由于沉积层与其下伏结晶基底存在着较大的波阻抗差异, 因此在P波接收函数波形中包含了来自沉积层转换波及其多次波信号。为此, 首先通过正演模拟来展示沉积层产生的多次波对P波接收函数的影响。设置地壳总厚度为40 km,通过改变沉积层的厚度, 对比二轴坐标系(Z-R-T)和三轴坐标系(L-Q-T)下获得的P波接收函数, 从而认识沉积层产生的多次波对P波接收函数的影响。表 1为模型参数, 假定模型中的介质为水平层状各向同性介质, 射线参数设为 6.4 s/°, 高斯系数α设为 2.0, 改变沉积层厚度从 1 km 至 9 km, 运用Frederiksen and Bostock (2000)的方法获得了Z-R-T坐标系(图3)和L-Q-T坐标系(图4)的P波接收函数。
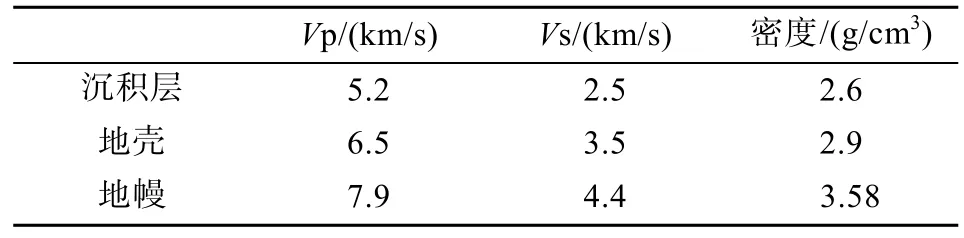
表1 模型参数设置Table 1 Model set
图3为Z-R-T坐标下的正演P波接收函数。当沉积层厚度在1~5 km之间时, 结晶基底产生的Pbs信号受到直达P波的压制, 特别当沉积层厚度较浅时, 这种压制更为明显。与此同时, 沉积层产生的多次波 PbpSs和 PbsPs也一定程度地压制了 Moho面转换波 Pms信号。尤其明显的是, 当沉积层厚度较大时(约8 km), Pms信号受到的压制更为显著。随着沉积层厚度的增加, 使得 Pms信号及其对应多次波信号到时发生了延迟。
而基于L-Q-T坐标下的P波接收函数(Q分量),在Q分量上仅为转换SV波能量并无直达P波能量(图4), 去除了直达P波的影响, 因此浅部沉积层的Pbs信号得以凸显。同样地, 在沉积层厚度为 8 km时, 沉积层产生的多次波明显地压制了Moho面Ps转换波。图3和图4正演结果显示: 由两种不同旋转方法获得的P波接收函数, 在沉积层到达一定厚度时, 产生的多次波会压制Pms信号, 而来自Moho面的 PmpPs多次波信号清晰稳定, 因此在含有巨厚沉积的研究区域, Moho面的PmpPs多次波信号常被用于壳幔结构的偏移成像(Chen et al., 2006;Nábělek et al., 2009)。
Z-R-T旋转(图3)和L-Q-T旋转获得的P波接收函数(图 4), 均能观测到沉积层产生的 PbpSs和PbsPs多次波, 且极性均为负。因此在利用P波接收函数来讨论盆地壳内存在的低速界面时, 应注意,可能不是真实的低速界面, 而是沉积层的多次波。
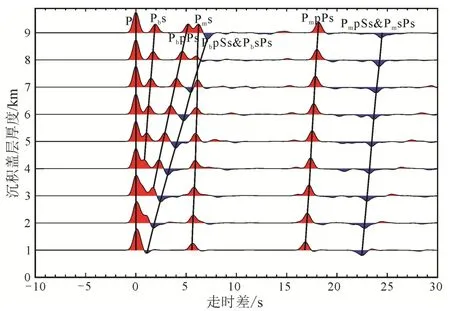
图3 基于二轴旋转正演获得的P波接收函数(R分量)Fig.3 Synthetic P receiver functions (R component)based on the Z-R-T system
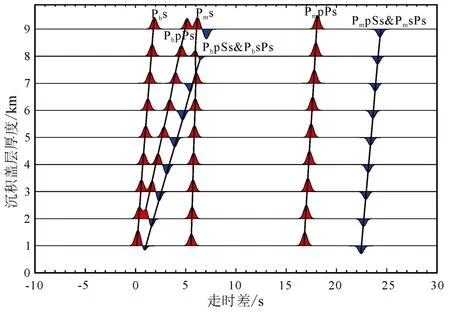
图4 通过三轴旋转正演获得的P波接收函数(Q分量)Fig.4 Synthetic P receiver functions (Q component)based on the L-Q-T system
运用H-κ叠加方法(Zhu and Kanamori, 2000)能够估算出地壳平均厚度及Vp/Vs比值。针对上述正演结果, 选择沉积层厚度为8 km时在L-Q-T坐标下生成的理论P波接收函数进行H-κ扫描。扫描参数w1为0.7,w2为0.2,w3为0.1, 设定Vp为6.3 km/s。由H-κ扫描获取的地壳厚度值为46 km(图5), 与模型设定的40 km地壳厚度存在较大出入。不难看出,由于存在巨厚的沉积层, 利用 H-κ扫描方法无法获取正确的地壳厚度。
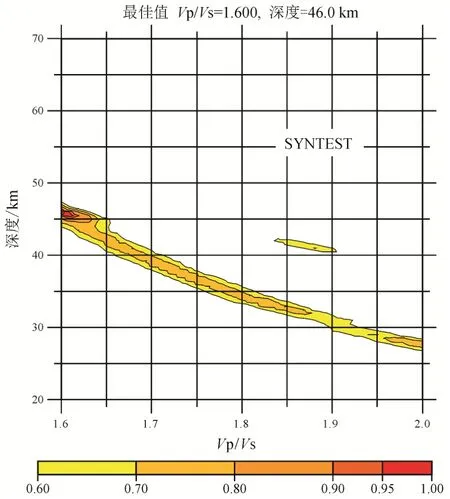
图5 L-Q-T坐标下含有8 km厚沉积层的PRF进行H-κ扫描获得的地壳厚度与Vp/VsFig.5 H-κ results of the synthetic PRF including an 8 km thick sedimentary layer on the top
3 不同沉积层厚度对S波接收函数影响
P波接收函数中的Pms转换波之后会跟随其壳内产生的多次波震相, 且这些壳内多次波信号的幅值有时大于 Pms转换波信号。另外, 由于来自浅部上地幔不连续界面信号的慢度值与壳内多次波的慢度值相近, 此二者信号几乎在同一时间窗口内到达, 从而使得P波接收函数很难获取上地幔不连续界面信息。针对上述情况, Farra and Vinnik(2000)首先提出了 S波接收函数(S receiver function, 简称SRF)。由于S波在壳幔不连续面产生的Sxp转换波(这里 x指多种界面)速度较快, 能早于多次波到达(Farra and Vinnik, 2000; Yuan et al., 2006), 常被用于探测壳幔内部的不连续界面。但是, 由于远震体波的直达S波在P波之后到达, 其能量相对于直达P波弱且受到P波尾波的影响, 使得S波接收函数通常具有较低的信噪比。
与提取P波接收函数相似, 提取S波接收函数的过程同样包括了坐标旋转、滤波、反褶积等三个步骤。最后通过时间域反褶积计算后, 即可得到S波接收函数。此时, Smp信号能量在 L分量上,SV波能量在Q分量上。为了提高Smp信号的信噪比, 将单台获得的多个SRF叠加。与PRF叠加所不同的是, 依据单个SRF信噪比给予其不同的叠加权重进行叠加(Farra and Vinnik, 2000)。
利用表 1所示模型, 正演模拟了不同沉积层厚度对 SRF的影响。考虑实际计算所得的SRF的频率相对较低, 正演合成SRF时, 采用截止频率为3 s的低通滤波器。图6所示的正演模拟结果表明不同厚度的沉积层对Moho面产生的Smp转换波几乎没有干扰。
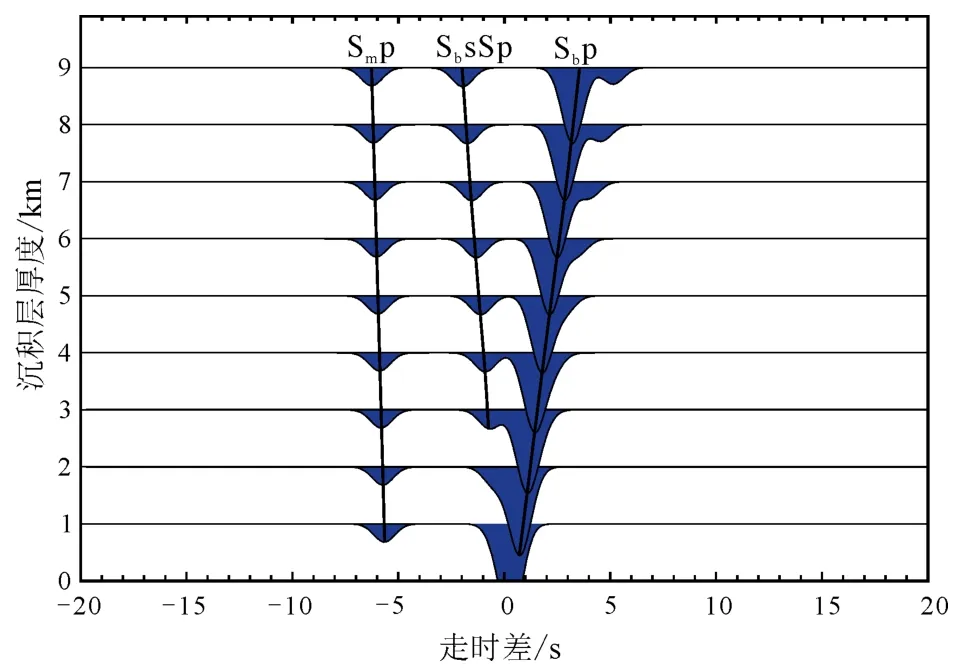
图6 含沉积层的S波接收函数正演结果Fig.6 Synthetic SRF includes a sedimentary layer on the top
此外, 表 2给出的模型考虑了未固结的松散沉积层。图7所示的正演结果表明, Smp信号没有受到未固结的松散沉积层多次波较大影响。因此在盆地区域内, 除了利用传统的PRF, 加入SRF能更有效地压制沉积层的干扰, 较为准确地获得盆地下方的壳幔结构特征。

图7 设定沉积层为松散沉积下的SRF正演结果Fig.7 Synthetic SRF contains loose sediments on the top
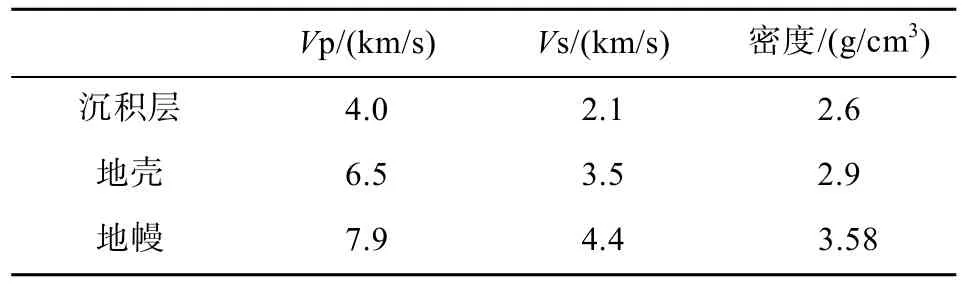
表2 包含松散沉积层的地壳模型Table 2 Crust model including the loose sediments on the top
4 压制沉积层影响方法
由前文正演可知, 对于 P波接收函数来说, 在沉积盆地区域, 由于沉积层多次波的效应, 可导致Moho面的转换Ps信号被压制甚至掩盖。因此, 在盆地区域进行P波接收函数分析时需考虑减小沉积层带来的信号压制效应。Yu et al.(2015)设计了一种共振滤波器(resonance filter)用以压制沉积层对Moho信号的干扰, 从而突出Moho信号。该滤波器在频率域的形式为(1+r0e-iωΔt),r0为P波接收函数首个波峰和首个波谷的幅值比, Δt是沉积层转换信号(Pbs)的双程走时, 可通过量取 P波接收函数首个波峰和波谷之间的时间差获得。在实际计算中, 上述两个参数的值可通过归一化自相关计算(normalized autocorrelation function)获得。
5 PRF和SRF联合反演
本文采用了 Vinnik et al.(2004)提出的 PRF和SRF联合反演方法获取台站下方的壳幔速度结构,该方法考虑了PRF和SRF接收函数不同尺度的分辨率特征, 在多个区域的壳幔结构研究中取得了良好效果, 如在中国新疆天山、土耳其南部的范湖(Lake Van)和覆盖有巨厚冰盖的格陵兰岛(Vinnik et al., 2006, 2007; Kiselev et al., 2008; Silveira et al.,2010; Morais et al., 2015; Kraft et al., 2019)。值得指出的是, 格陵兰岛地表覆盖的巨厚冰层对 P波接收函数的影响与沉积层的影响类似, 均为地表的低速盖层。本文采用基于 L-Q-T坐标下提取的 P波和S波接收函数, 联合反演共同约束壳内结构特征。
联合反演中, 假设台站下方的介质均匀且各向同性, 每次迭代反演是在指定的允许范围内运行四个独立的随机模型, 反演模型的最优解由模拟退火方法(Mosegaard and Vestergaard, 1991)求得。初始模型由9层组成, 前4层为地壳, 后5层为地幔, 每一层由Vp、Vs、层厚和密度所确定。其中, 密度是通过Vp值经Birch方程(Vinnik et al., 2004)换算得到。合成理论接收函数过程中, 利用了展平变换(Biswas, 1972)将深部地球曲面展平为平面以满足地震波平面波理论。反演过程中模型一直处于迭代拟合使得正演获取的接收函数与观测到的接收函数的拟合残差最小。模型正演是基于水平层状介质和平面波传播, 采用的是 Thomson-Haskell矩阵方法(Haskell, 1962)来计算理论接收函数。正演过程中,PRF中的正演Q分量和SRF中的L分量分别由以下方程获得。
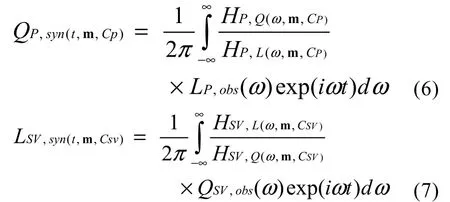
上述两式中,t表示时间,ω是频率, m是模型里的未知参数矩阵,CP和CSV是视速度, 角标 obs和syn分别表示实际观测到的接收函数和理论计算的接收函数,H是理论传递函数。
通过公式(8)计算实际观测到的接收函数和理论接收函数之间的拟合差。
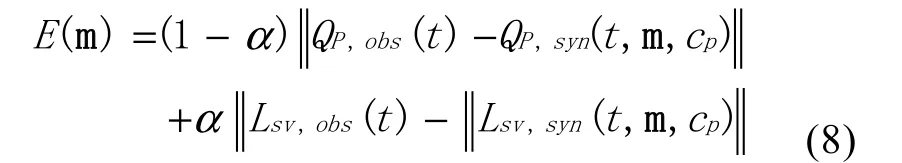
α为PRF和SRF之间的权重,E(m)为拟合差。实际计算中,α通常取值为0.5。上述公式求得的最小值即为反演的最优解。
为了更好地约束上地幔的速度, 在反演过程中还加入了 P波和 S波在上地幔传播过程中相对于IASP91(Kennett et al., 1995)的走时残差(Δtp 和 Δts),即通过计算地幔转换带顶界面(Pd410)和底界面(Pd660)相对于IASP91模型的走时差获得。通常在克拉通地区, Pd410和Pd660两界面之间的走时差值约为23.9 s(Kraft et al., 2019)。如果该值不变, 而Pd410和 Pd660的到时差发生了变化, 若整体延迟或整体提前, 即表示在地幔转换带之上的上地幔中存在速度异常体。若两界面到时整体延迟暗示了上地幔存在低速物质; 反之, 两界面到时整体提前指示了上地幔存在高速物质。如果地幔转换带的走时差与IASP91模型相近(约23.9 s), 通过拾取Pd410的到时差(ΔtP410)即可计算 P波和 S波的走时残差,依据 Vinnik et al.(1999), ΔtP410=Δts-Δtp, 而 Δts/Δtp的比值约为3。拾取Pd410的到时差是在基于延迟叠加方法(delay-and-sum)获得的波形上进行(如图10), 具体方法介绍见Vinnik(1977)。
为了将反演获得的速度模型可视化, 将参数空间划分为网格, 并通过颜色深浅表示每个网格的模型命中数。虽然此方法可以同时获得Vp和Vs速度结构, 但Vs的反演结果要比Vp的反演结果准确度相对更好。
6 结果讨论和分析
本文选取了位于盆地内部的两个台站, 分别是位于渭河盆地内部的台站 QS130和位于河套盆地内部的台站15693(图8), 通过联合反演获取两个台站下方的壳幔结构, 并将获得的 Moho深度结果与运用Yu et al.(2015)的方法将PRF进行沉积层校正后再进行H-κ扫描后得到的结果进行对比。
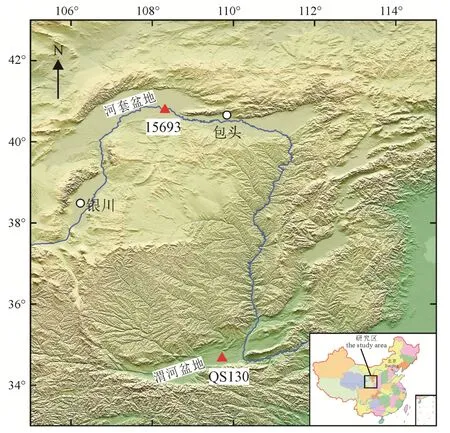
图8 样例台站位置分布图Fig.8 Distribution map of sample stations
中国地质科学院布置的台站 QS130观测周期为2012—2014年(Feng et al., 2017), 来自ChinArray的台站15693观测周期为2013—2015年(郑秀芬等,2009)。对于P波接收函数, 选取震中距为30°~95°,震级大于 5.4的地震事件。S波接收函数选择震中距65°~90°, 震级大于5.4的地震事件。
计算 PRF和 SRF, 对原始数据先依次经过Z-R-T旋转与 L-Q-T旋转, 再经带通滤波处理。然后, 采用时间域反褶积分别提取P波接收函数和S波接收函数。针对需要 H-κ扫描的 PRF, 使用30-2 s的带通滤波器进行滤波。在联合反演中, PRF使用30-5 s带通滤波器, 而SRF用的是30-8 s带通滤波器。最后挑选出高信噪比的PRF和SRF。台站QS130获得84条PRF和5条SRF, 台站15693获得 26条 PRF和 15条 SRF。得到的 PRFs和 SRFs经过动校正(校正采用的射线参数为 6.4 s/°), 最后将动校正后的PRFs和SRFs进行叠加以增强转换波信号(图 9)。
6.1 渭河盆地台站QS130
图9展示了QS130获得的P波接收函数(图9A)和S波接收函数(图9B)。渭河盆地内具有厚约3 km的沉积层(滕吉文等, 2014)。联合反演之前没有做沉积层校正, 以便验证联合反演方法克服沉积层影响的健壮性。正如前文所述, 在联合反演中引入了Δtp和Δts。考虑到不同的P410和Pd660之间的走时残差(Δtp和 Δts)可能影响到反演结果, 因此选择了三组不同的走时残差来进行反演测试。如图11A所示,tp=0 s、ts=0s表示没有走时残差, 这组值为真实计算所得(图10); tp=0.1 s, ts=0.3 s, 为上地幔存在低速物质导致 Pd410走时残差延迟了 0.2 s; 而tp= -0.1 s, ts= -0.3 s表示台站下方的上地幔存在高速物质导致Pd410走时残差快了0.2 s。
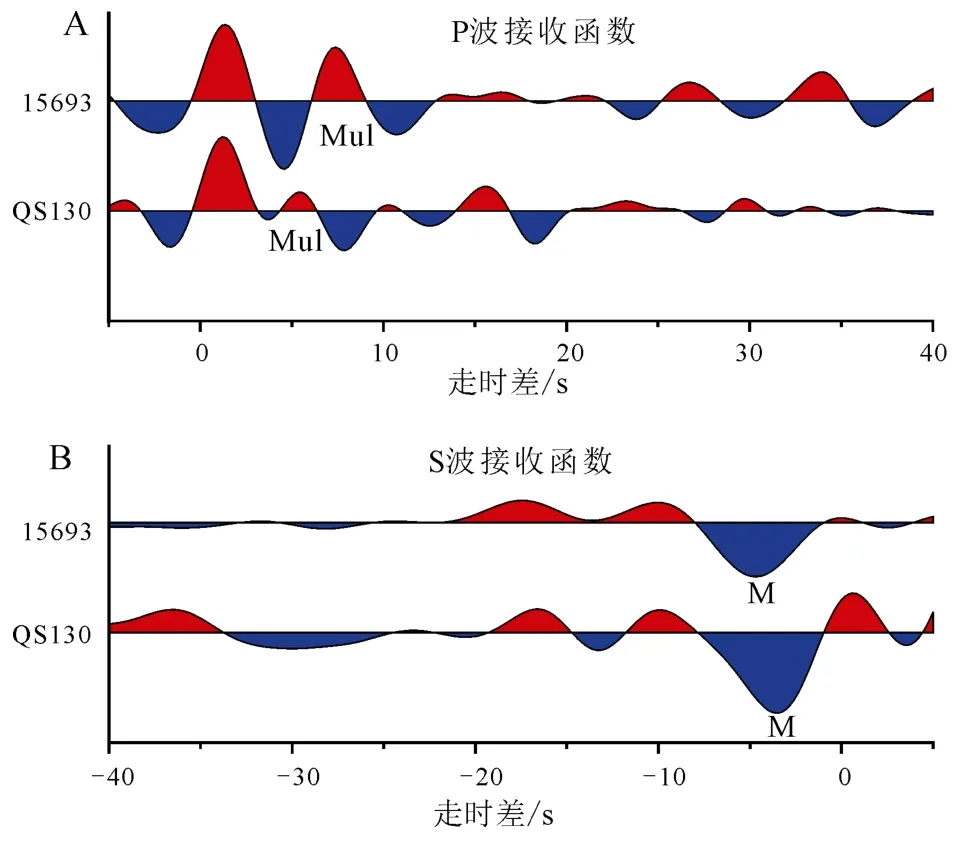
图9 QS130台站和15693台站(位置见图8)下方的PRF(A)和SRF(B)动校正后波形叠加图Fig.9 Stacked P (A) and S (B)receiver functions after moveout correction of station QS130 and 15693(location can be seen in Fig.8)
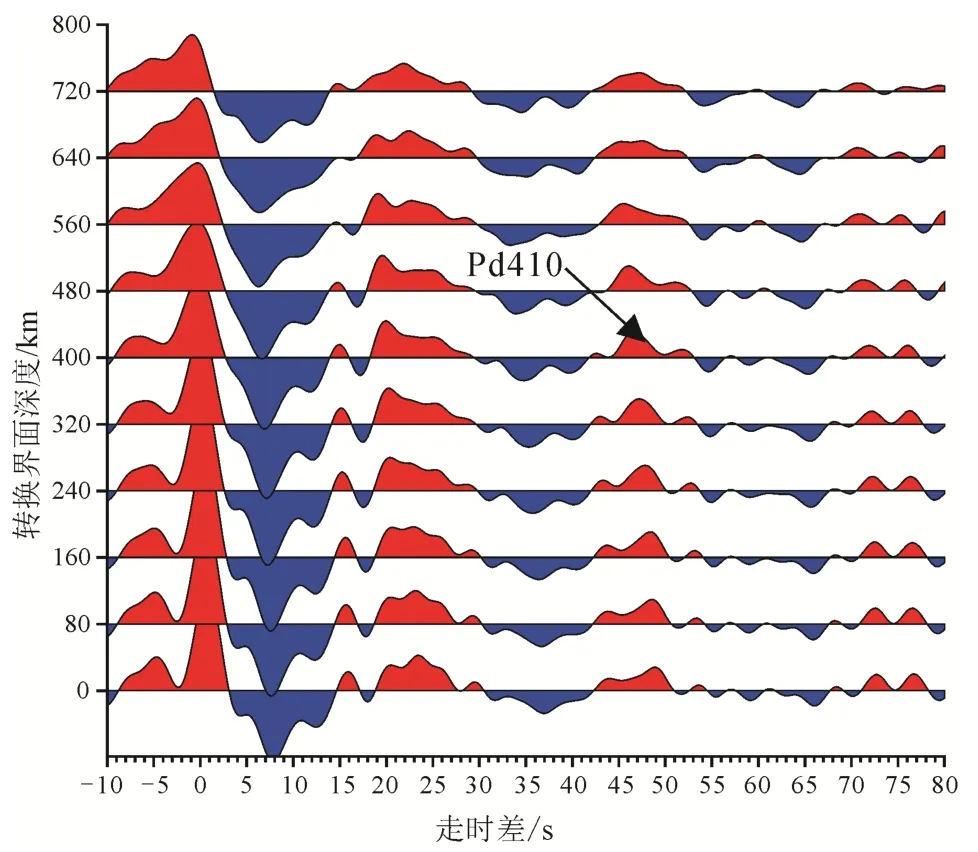
图10 延迟叠加方法得到的QS130台站PRFs叠加后波形图Fig.10 The PRFs stacking results of QS130 station by applying delay and sum method
联合反演结果显示, 不同的走时残差组得到了相近的地壳速度结构(图11), Moho深度约在35 km,误差范围约在±2 km, Vs速度从约3.7 km/s跃迁至约4.4 km/s, 而Vp速度结果则相对变化较大。相比之下, 图11A所展示的tp=0 s,ts=0 s这一组给出了更好的拟合结果, 因为通过真实计算 Pd410和Pd660的走时残差获得的ts的直方图更为规则。对于Vp来说, 地幔的速度值低于IASP91模型, 这可能是因为地幔中存在相对较多的辉石(Vinnik et al.,2016), 使得Vp速度偏低而Vs速度不变, 如图11A所示的Vp/Vs的值分布特征。对于地壳来说,Vp/Vs的值与IASP91模型接近一致, 进入地幔后由于Vp的减小导致Vp/Vs的比值降低。反演结果与该区域的主动源地震探测结果一致(滕吉文等, 2014), 即Moho深度约为36 km (图11A)。
此外, 图 11所示的反演结果中第一层为沉积层,Vs约为2.04 km/s, 厚约3 km。在深约11 km处观察到另一界面, S波速度约3.0 km/s,Vp速度约为5.8 km/s, 这一界面探测结果同样可与滕吉文等(2014)结果对比(深约 15 km 和Vp速度约为6.2 km/s)。反演结果显示中下地壳Vs约为3.65 km/s,与IASP91模型关于中下地壳的Vs速度值3.75 km/s接近, 为正常中下地壳。
另外由三轴旋转计算得到的PRFs, 运用Yu et al.(2015)方法做了沉积层影响的校正, 再利用 H-κ方法分析了校正沉积层影响前后的PRFs。扫描过程中所有参数一致, 即设定w1为0.7,w2为0.2,w3为0.1。Vp设定为6.5 km/s。如图12A所示校正前的H-κ结果受沉积层多次波的干扰导致 H-κ获得的Moho深度值为 48.5 km, 明显与主动源探测结果(滕吉文等, 2014)存在较大的差别。而图12B所示校正后的 PRFs经 H-κ扫描获得的 Moho深度值为37 km, 与主动源探测到的Moho深度36 km(滕吉文等, 2014)具有较好的一致性。因此, 在本次研究中通过P波与S波接收函数联合反演获得的Moho深度(图 11A)与利用 H-κ扫描沉积层影响校正后接收函数得到(图 12B)相互一致, 表明进行沉积层校正后的PRFs能较为准确地探测出地壳厚度。
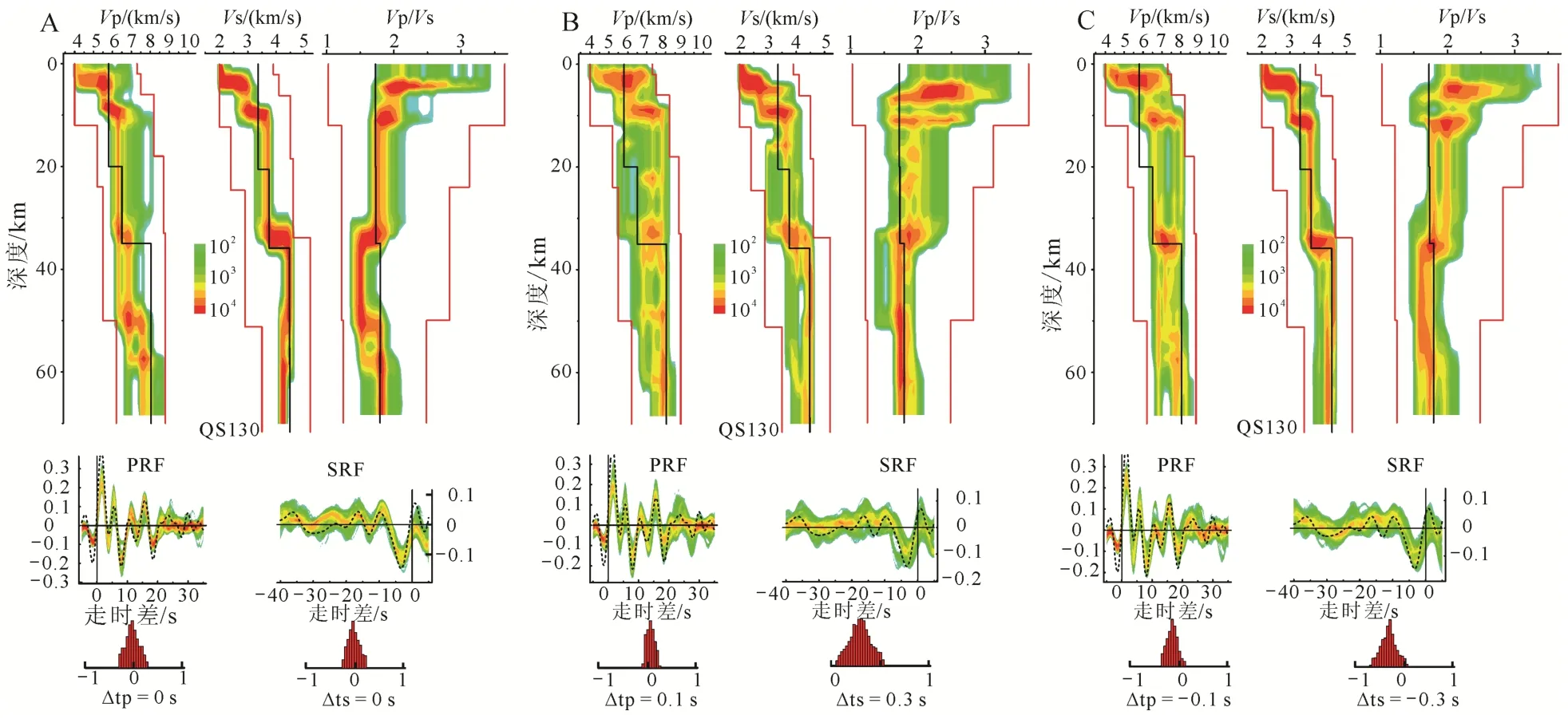
图11 台站QS130三组不同走时残差(Δtp和Δts)得到的反演结果Fig.11 Inversion results of QS130 with three sets of travel time residuals
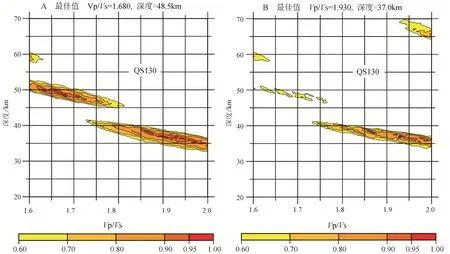
图12 台站QS130进行沉积层校正前后的H-κ叠加结果Fig.12 The H-κ result of QS130 station
校正后 H-κ扫描所得的Vp/Vs值为 1.93(图12B), 而图11A所示, 排除地表沉积层, 整个地壳κ值的平均值约为1.75。而盆地顶部松散沉积层的存在会导致最终获取的κ值明显升高。结合本文通过联合反演获得的Vs速度结果(图11A)和Vp/Vs结果(图12B), 认为台站QS130下方地壳高κ值1.93是由于约3 km厚的沉积层干扰所导致, 台站QS130下方的地壳组分应为正常组分, 这也与主动源探测结果(滕吉文等, 2014)一致。
6.2 河套盆地台站
台站 15693位于河套盆地内部, 其北为阴山山脉, 其南为河套盆地, 盆地内部存在较厚沉积物。通过 H-κ扫描法分析 P波接收函数校正前后结果(图 13), 显示尽管两者之间 Moho深度值较为接近, 但校正后的H-κ扫描结果(图13B)更为聚焦。
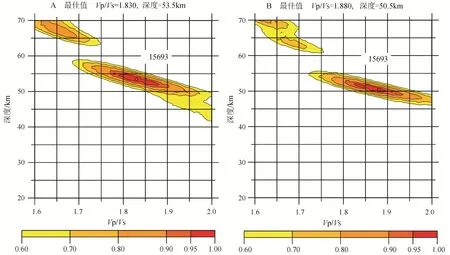
图13 台站15693做沉积校正前(A)、后(B)的H-κ叠加结果Fig.13 The H-κ result before (A) and after (B) applying resonance filterin of 15693 station
P波、S波接收函数联合反演结果(图 14)显示,Moho在约(49±2) km深处,Vs速度值从3.70 km/s跃升至4.48 km/s。联合反演的结果(图14)与校正后的PRFs通过H-κ扫描获得的Moho深度值(图13B)接近。此外, 图14显示该台站下方~33 km至~49 km之间下地壳存在低速层,Vs速度约为3.70 km/s, 低于IASP91模型中下地壳的Vs速度值。大地电磁探测结果表明该区域下方存在低阻高导层(Dong et al.,2014), 能印证联合反演所获得的低速层结果。本文所获得的结果与利用不同的地球物理探测手段获得结构特征较为一致, 表明本文利用L-Q-T坐标下的P波与S波接收函数联合反演获取地壳结构特征是可行的。
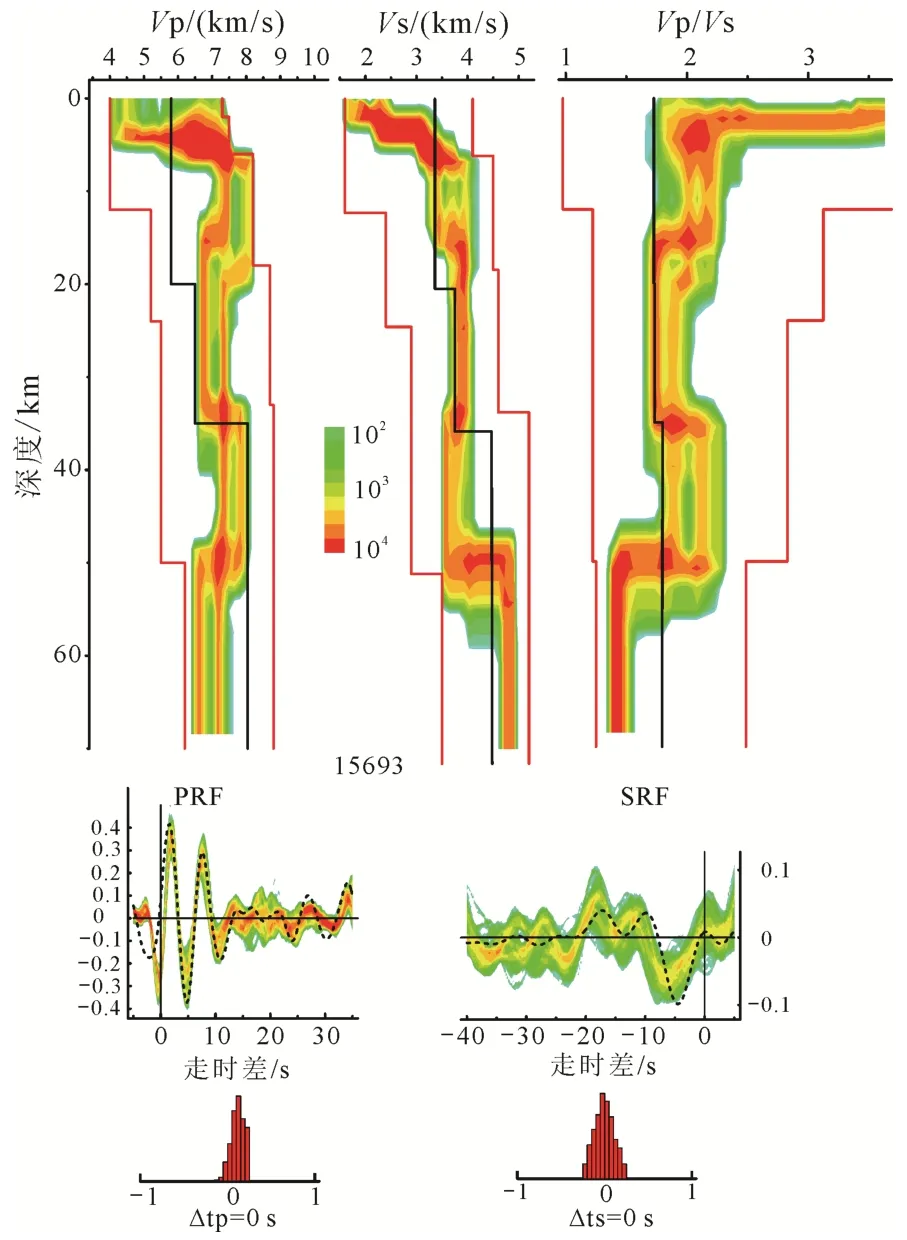
图14 台站15693联合反演结果(Δtp= 0s, Δts= 0s)Fig.14 The inversion result of station 15693 by putting Δtp= 0s, Δts= 0s
7 结论
在沉积盆地地区, 沉积层产生的多次波对Moho转换波信号产生了压制, 导致 H-κ方法不能有效估算地壳厚度和物质组分。本文利用L-Q-T坐标下提取到的 P波和 S波接收函数, 使用 P波、S波接收函数联合反演方法获得台站下方壳幔结构特征, 可与主动源地震探测结果对比。此外, 在L-Q-T坐标下提取到的 P波接收函数, 经沉积层校正后(Yu et al., 2015), 再用H-κ方法能够较为准确地获得地壳厚度。总之, L-Q-T坐标下进行P波和S波接收函数联合反演, 不仅能获取地下结构信息,而且能获取速度信息, 能更好地认识研究区地球动力学演化过程。
致谢: 感谢俄罗斯科学院地球物理研究所Lev Vinnik教授提供的联合反演程序和德国地学研究中心(GFZ)Xiaohui Yuan教授提供的H-κ扫描程序。感谢中国地质科学院地球深部探测中心安美建研究员提供台站QS130天然地震观测资料, 感谢中国地震局地球物理研究所“中国地震科学探测台阵数据中心”为本研究提供台站15693地震波形数据。
Acknowledgements:
This study was supported by China Geological Survey (Nos.DD20221643-4 and DD20190015), and National Natural Science Foundation of China (No.42074112).
