低维石墨烯体系中的离域磁性*
2022-09-30郑玉强王世勇2
郑玉强 王世勇2)†
1) (上海交通大学李政道研究所,上海 200240)
2) (上海交通大学物理与天文学院,上海 200240)
由于量子效应,低维石墨烯体系中具有离域的p 壳层磁性,其性质迥异于局域的d/f 壳层电子.该离域特性使精准调控纳米石墨烯的磁基态和磁交换作用变得有可能,有望精准构筑高质量的磁性石墨烯量子材料.近年来,由于表面化学和表面物理的深度结合,在单原子精度下研究纳米石墨烯的磁性变为可能,打开了一个研究有机量子磁体的新方向.本综述首先概述纳米石墨烯磁性的发展过程和研究现状,然后讨论纳米石墨烯中磁性的产生机制,接着回顾近年来实验的研究进展,最后对低维磁性石墨烯未来发展可能遇到的挑战与机遇进行展望.
1 引言
磁性一直以来都是物性研究的重点性质之一,理论上有很多描述磁性行为的方法,例如海森伯模型、伊辛模型和量子蒙特卡罗等[1-3].低维磁性的研究不但对自旋电子学器件的应用有着重要意义,而且在未来量子计算与量子器件的发展中有着广阔的应用前景.如构建自旋逻辑器件[4-6]与基于磁性单分子设计磁性分子开关等[7,8],而磁性原子链与超导表面结合诱导出马约拉纳准粒子,可用于自纠错的拓扑量子计算等[9,10].化学领域对磁性的研究也产生了许多重要的成果,如磁性原子与有机分子形成的金属有机框架有着众多的应用[11,12].材料科学通过分子束外延、解离、晶体生长等技术制备众多品质优异的磁性材料.利用二维材料转移技术,可以制备出堆叠角度可控的几层材料,其中魔角石墨烯中更是展现了轨道磁性[13-16].但是,如何精准制备只有几个自旋的低维量子磁性系统仍然是材料制备方向的难题.
石墨烯是由两套三角子格构成的蜂窝形格点,当打破石墨烯两套子格的对称性时,将引入π 电子磁性.追溯到20 世纪末,Ovchinnikov[17]和Lieb[18]在对蜂窝状格点的研究中发现,当两套子格的碳原子数目不相等时,系统的基态会出现净自旋,自旋数目与子格不配备程度相关.因此,通过设计纳米石墨烯的拓扑结构,引入子格不对称,可以实现磁基态和磁交换作用的精准调控.将单个纳米石墨烯视为一个“磁性原子”,理论上可以构筑任意精准可控的低维量子磁性体系.与传统过渡金属的d 轨道和f 轨道电子磁性相比,由于碳元素更轻,π 电子磁性会表现出弱自旋-轨道耦合、长自旋相干时间和长相干长度[19-23]等优点,有望构筑高性能石墨烯量子材料,解决量子信息技术方面的难点.这些原因使碳基材料的磁性显得越来越重要,相关研究成为当前凝聚态物理前沿的重点方向之一.
理论研究表明即使是单原子的缺陷也会极大破坏纳米石墨烯的磁基态,因此实验研究需要结构原子级精准的样品,这对样品制备和表征都提出了极高的挑战.如何制备结构原子级精准的样品成为了该方向需要首先解决的核心科学难题.化学上,利用溶液合成方法能够制备分子量低的磁性纳米石墨烯,但是由于自由基的存在,相关分子在大气环境下极不稳定,容易被氧化而失去磁性.因此研究者们只能通过添加保护性基团合成一些磁性纳米石墨烯的衍生物[24],通过电子自旋共振(electron spin resonance,ESR)测量验证了这些化合物是具有未配对的π 电子[25,26].2007 年,Grill 团队[27]开创了在金属表面利用分子共价组装合成低维纳米结构;2010 年,Fasel 团队[28]利用“自下而上”的策略,类似于搭积木发展了一类普适的制备石墨烯纳米带的新方法.随后这些表面合成的手段成功拓展到纳米石墨烯的合成中来: Fasel 团队首先利用溶液合成制备具有特定官能基团的分子前驱体;然后借助表面化学合成得到目标低维石墨烯产物[28].该“自下而上”的方法理论上可以合成任意的低维石墨烯结构,具有高度的可调节性和可设计性,将石墨烯材料的制备能力提升到了单个原子精准上.结合超高分辨的扫描隧道显微镜技术(scanning tunneling microscopy,STM)和非接触原子力显微镜技术(non-contact atomic force microscopy,nc-AFM),使得在单原子精度下研究纳米石墨烯的磁性变为可能.
2016 年以来,陆续报道了不同磁基态的纳米石墨烯单体,其具有自旋单态、双态、三态等不同磁基态[29-56].通过设计磁性纳米石墨烯的自旋密度交叠方式,其磁交换作用可以被精准地调控.目前最大的磁交换强度能达到102 meV[47],远远超过了室温下依旧保持磁交换所需要的强度阈值,有望设计出在室温工作的自旋电子器件[57].利用纳米石墨烯单元可以构建任意可控的低维量子磁性系统,实现了在实空间对量子磁性体系的精准表征,例如实验上首次在实空间验证了Haldane 量子自旋链的拓扑模型[48,51],证实了从磁性纳米石墨烯出发构建更为复杂的低维磁性系统的可行性.这些前期研究工作展现了纳米石墨烯π 磁性的独特魅力以及未来的发展潜力.如图1 所示,对纳米石墨烯的磁性研究主要聚焦在3 个方面: 1)精准的化学合成,用以制备不同结构的原子级精准的样品;2)构筑低维量子自旋系统,在单原子精度下研究低维量子磁体,并和凝聚态强关联理论实现有机结合;3)构筑磁性纳米石墨烯-超导异质结,其中具有丰富的拓扑超导效应,可以用来实现自纠错的拓扑量子计算.

图1 石墨烯磁性研究的3 个重点 1) 精准化学合成: 制备不同结构的原子级精确的纳米石墨烯.2) 低维量子磁性: 基于磁性纳米石墨烯构建低维量子自旋系统.3) 超导近邻效应: 纳米石墨烯磁性与超导相结合Fig.1.Three important directions for studying graphene quantum magnetism.1) Precise chemical synthesis: preparation of atomically precise nanographenes with different structures.2) Low-dimensional quantum magnetism: construction of low-dimensional quantum spin system based on π-magnetic nanographene.3) Proximity effect of superconductivity: combination of π-magnetic nanographene with superconductivity.
本文综述了近几年有关纳米石墨烯π 磁性的研究工作.首先概述了石墨烯π 磁性的发展历程,第2 节将分别从经验公式和理论计算(平均场近似的Hubbard (mean-field Hubbard,MFH)模型、密度泛函理论 (density functional theory,DFT))的角度对纳米石墨烯磁性起源进行讨论;第3 节从表面化学合成、STM 针尖操纵的方式概述纳米石墨烯的合成方法;第4 节从不同磁基态的电学、磁学响应以及磁耦合的角度分析纳米石墨烯的性质;最后对磁性纳米石墨烯研究领域的发展以及未来可能遇到的挑战提出总结和展望.本综述主要讨论近年来磁性纳米石墨相关的研究,旨在系统介绍该方向的发展.纳米石墨烯相关材料的理论计算[58]、合成与性质[59-61]、表面合成[62-66]、绝缘体表面反应[67]、表面磁性原子与低维磁性系统[68-70],这些方面都有比较好的综述且侧重点不尽相同,这里部分列举就不再赘述.
2 π 磁性起源
2.1 计算方法
石墨烯是由sp2杂化的碳原子构成的蜂窝状二维材料,其原胞内包含两个碳原子,隶属于AB两套子格.每个碳原子与最近邻的3 个碳原子形成3 个σ 键,剩余一个电子占据pz轨道参与形成大的共轭π 键,即π 电子.根据泡利原理可知,AB格点π 电子应当占据不同的自旋态.σ 电子的能带远离费米面,因此石墨烯的基本性质来源于半填充的π 电子.π 电子的哈密顿量可以写为

其中,Te表示格点上π 电子的动能项,VeN表示电子与格点离子实的势能项,Uee表示电子-电子之间的相互作用.为了描绘体系的主要特征,先忽略电子间的复杂多体过程和高阶的电子跃迁,只考虑最近邻格点间电子的跃迁和格点上电子的势能,此为紧束缚模型,系统哈密顿量可改写为


其中,α是格点i上电子的自旋,h.c.是哈密顿量厄密共轭部分.对于石墨烯体系t的取值一般为2.7 eV[58,71],该紧束缚模型能够定性地描绘石墨烯能带结构的主要特征.
当二维的石墨烯变成一维的纳米带以及零维的纳米结构时,维度降低带来量子限域系统地增强,电子的关联效应变得不可忽视.因此,想要进一步描绘石墨烯体系中磁性的起源,则必须重新考虑电子间的在位库仑相互作用,即(1)式中的第3 项[72].
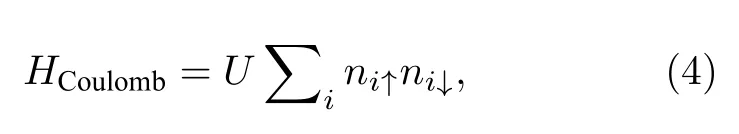
其中,U是格点i上电子的在位库仑排斥,ni↑(↓)表示自旋相关的电子密度.对于多原子多电子这样的复杂多体系统,可以通过平均场近似将电子-电子间的多体相互作用简化为单电子与剩余电子平均背景间的单体相互作用,因此平均场近似下电子间相互作用的哈密顿量可以写为
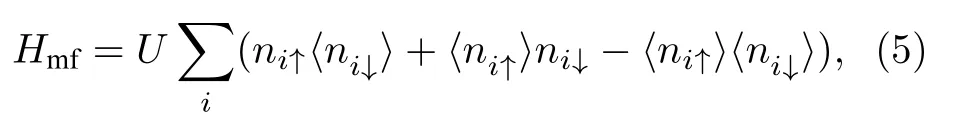
其中〈ni↑(↓)〉表示自旋相关的平均电子密度.平均场近似忽略了高阶涨落间的作用,因此系统是处于足够低的温度.此时总的哈密顿量可以写为

给定〈ni↑(↓)〉合适的初始值,通过迭代运算就可以使系统的能量收敛,从而求解出格点上自旋分布的本征值.对于每一个格点的自旋可以得到

那么,系统的净余自旋则是:

可以看到纳米石墨烯中磁性的产生与t和U的取值有着密切联系.如图2(c)所示,对于磁性纳米石墨烯,当U=0 时,仅考虑最近邻格点电子跃迁可以得到纳米石墨烯在费米面附近有半填充的零能态,但无法得到电子实际的占据情况[30].当U=3.5 eV 时(这里U的取值是石墨烯体系的常用参数,实际计算中U可以取任意值),如图2(d)所示,这些零能态则发生自旋极化,导致库仑能隙的打开,原来的零能态劈裂为关于费米面对称的一对单占态,费米面下的占据态和费米面上的空态具有相反自旋[30].如果体系本来具有两个零能态,就会劈裂为两组单占态,可以看到对于不同体系,单占电子的磁基态是不同的,比如三角烯的磁基态是铁磁[30],而克拉尔杯(Clar’s goblet)的磁基态是反铁磁[34].
除紧束缚模型外,DFT 也广泛应用在石墨烯纳米结构的研究中,相较于MFH 模型的优势,DFT可以考虑结构优化、衬底效应和元素掺杂对磁基态的影响等[73].后文主要利用MFH 模型讨论纯碳材料的磁性,对于元素掺杂的纳米石墨烯体系,DFT计算更加有效.
2.2 纳米石墨烯的磁性起源
上述MFH 计算方法在纳米石墨烯磁基态的计算中表现出色,并且能够很好地描述纳米石墨烯格点上的电荷密度、自旋密度,体系的轨道能级/能带结构,以及局域态密度等信息[74].近年来关于磁性纳米石墨烯的计算,其磁性起源主要可以归纳为4 种: 1) 子格不对称;2) 拓扑阻挫;3) 芳香苯环;4)拓扑缺陷.
第1 类π 磁性起源于子格不对称,对于石墨烯这样的双子格半填充体系,子格不对称可以理解为自旋不对称.如图2(a)所示,Lieb[18]通过Hubbard模型计算这种体系基态时发现,当AB子格数目不相等,系统的基态有净自旋:
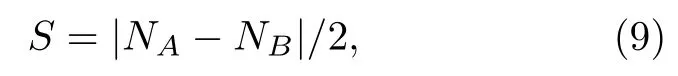
其中,NA和NB分别表示A和B子格碳原子数目.打破子格对称性可通过引入缺陷(比如碳空位[75,76]、碳杂环[77-80]、元素掺杂[81-86])等手段来人为实现.相关的方法均可以简化为引入双子格不对称,从而改变磁基态.具有代表性的结构为三角烯,其子格不匹配程度与三角烯分子的大小相关(见图2(a)).
第2 类π 磁性来源于拓扑阻挫,即π 电子网格的拓扑结构无法保证所有的π 电子都两两配对,因此出现单占据能级.与第1 类不同,这类结构的AB子格数目相等,根据Lieb 理论,其净自旋为0.Fajtlowicz 等[87]从图论的角度提出了一种计数规则,判断AB子格二分图本征值的数目,该数目对应于紧束缚模型中的零能态的数量,利用零值η(nullity)来表示,

其中,α是不相邻格点的最大可能数目,N是格点的总数目.如图2(b)所示,Clar’s goblet 分子AB子格数目相等,其不相邻格点的最大可能数目α=20,格点总数N=38,因此η=2,即两个单占据的零能态.其中,两个未配对电子分别位于AB两套子格,所以磁基态是开壳S=0 的自旋单态(又称为自旋极化态,即自旋分别分布在不同的空间),与平均场近似的计算结果相符.值得注意的是,Clar’s goblet 分子中两个自旋的反铁磁排列似乎与洪特规则相矛盾,洪特规则要求自旋按铁磁排列,这里可以解释为两个自旋分别属于AB两套子格,两者之间相互独立,同时碳-碳键要求最近邻的两个自旋反铁磁排列,因此AB子格上的自旋呈反铁磁满足这个要求.此外,从图2(j)所示的自旋密度计算结果可以看出两个自旋主要分布在分子两端的两套子格上.
第3 类π 电子磁性起源于芳香苯环,其中分子的子格守恒,且零值η=0 .如图3 所示,对于一个苯环,每个碳原子都是sp2杂化的,相邻碳原子通过碳-碳单键和碳-碳双键连接,这样苯环就有两种单双键交替的结构,这两种结构能量相等,因此基态为两种结构的叠加态,可以用大π 键的方式表示该芳香苯环(其中所有键长一样),这个简并的结构相较于单双键交替的苯环结构具有更低的能量.在化学中,分子具有更多芳香苯环,系统能量就越低,结构就越稳定.对于一个纳米石墨烯结构,如果能够画出具有更多的芳香苯环数目,那就意味着该结构可能具有更低的能量[88-90],如图3(b)所示,但在引入额外的芳香苯环过程中,同样会打破体系的共轭性,从而在体系中引入更多的未配对电子,其会增加系统的总能量.以并苯分子为例,我们可以画出不同的π 电子拓扑结构: 1) 具有一个芳香苯环,0 个未配对电子;2) 具有两个芳香苯环,2 个未配对电子;3) 具有3 个芳香苯环,4 个未配对电子.其基态取决于芳香苯环降低的能量与打破共轭性而增加的能量相竞争.平均场计算表明,并苯长度小于6 个苯环时,其基态为闭壳结构;长度大于6 个时,基态为开壳结构,其磁基态为自旋单态[91].除了并苯以外,纳米石墨烯中的超庚烯(superzethrenes)也有类似转变.随着长度n的增加,超庚烯会由闭壳转为开壳,其中n=5 的磁基态为闭壳,而n=7 的其磁基态为自旋单态[33,50,92].
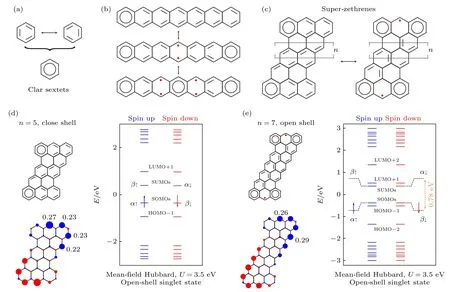
图3 π 电子磁性起源于共振苯环 (a) 共振苯环结构;(b),(c) 分别为并苯和超庚烯的磁性转变;(d) n=5 超庚烯的分子结构、MFH 模型的能级分布和单占电子的自旋密度分布,磁基态为闭壳[33];(e) n=7 超庚烯的分子结构、MFH 模型的能级分布和单占电子的自旋密度分布,磁基态为开壳[50] ((d),(e)出自文献[33,50],已获得授权)Fig.3.Clar sextets-induced π-magnetism: (a) Structure of Clar sextets;(b),(c) magnetic transition in acenes and super-zethrenes,respectively;(d) molecular structure,the distribution of energy level and single-occupied electrons spin density of n=5 superzethrenes,where magnetic ground state is close shell[33];(e) molecular structure,the distribution of energy level and single-occupied electrons spin density of n=7 super-zethrenes,where magnetic ground state is open shell[50] ((d),(e) reproduced with permission from Ref.[33,50]).
第4 类π 磁性起源于拓扑缺陷,石墨烯结构为蜂窝状结构,但是可以在其中引入拓扑缺陷,例如引入碳4 环、碳5 环、碳7 环等[56,77-80].引入拓扑缺陷,打破了石墨烯二分图构型,在体系中一些碳原子不能简单地划分为A子格或B子格.如图4(a)所示,平均场理论计算表明,在纳米石墨烯中引入两个碳5 环,体系仍为闭壳的基态;当体系结构稍微改变一些,两个碳5 环缺陷分别引入一个未配对π 电子,体系变为开壳S=0 或S=1 的基态[93].因此,通过精准地设计拓扑缺陷的排列,可以在纳米石墨烯中实现具有高自旋的磁基态,一维铁磁自旋链以及二维铁磁格点等[54](见图4(b)).实验上,虽然陆续制备了多类具有拓扑缺陷的纳米石墨烯,但是其磁基态受到衬底的影响很大,无法在金属衬底上观测其本征的磁基态[52,54,94-96].因此,为了研究拓扑缺陷导致的磁性,需要在绝缘衬底上制备纳米石墨烯结构,使其与金属衬底脱耦合.
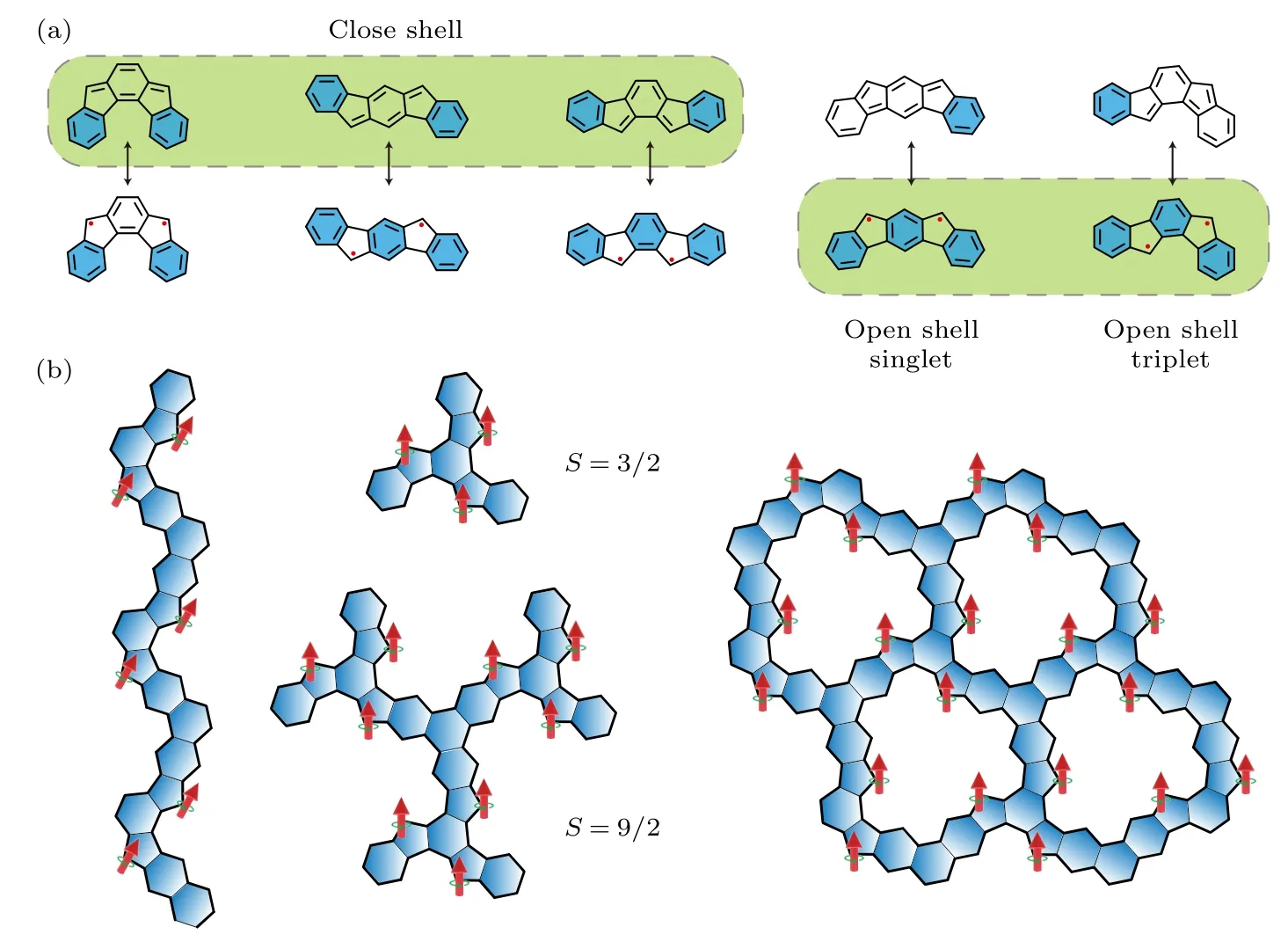
图4 π 电子磁性起源于拓扑缺陷 (a) 双碳五环纳米石墨烯不同构型的磁基态[93];(b) 基于碳五环可设计的高自旋结构[54]Fig.4.Topological defect-induced π-magnetism: (a) Magnetic ground states of nanographenes with double carbon-five-rings in the different configurations[93];(b) design of high spins structures based on carbon-five-rings[54].
3 纳米石墨烯的精准合成
从第2 节的理论计算表明,磁性纳米石墨烯的磁基态与π 电子的拓扑构型高度相关,单原子量级的缺陷就将破坏其磁性,这对样品制备提出了很高的挑战,需要精准地制备结构原子级精准的纳米石墨烯样品.最近表面化学和溶液合成化学的有机结合,解决了该样品制备的难点问题.表面化学合成的核心是采用具有一定催化活性的金属固体表面作为化学反应的平台,而不再是传统的溶液[97].这就带来了以下优势: 首先,固体表面代替有机溶剂,使得表面化学合成可以在超高真空环境中进行,能有效避免未配对电子被氧化、溶剂等污染物的影响;其次,可以与众多超高真空环境中工作的表面敏感技术相结合,比如STM、nc-AFM、X-射线光电子能谱(X-ray photoelectron spectroscopy,XPS)、针尖增强拉曼光谱(tip-enhanced Raman spectroscopy,TERS)等[98-100],对合成产物可以得到超高分辨的空间结构和丰富的物性信息.最后,由于化学反应被限制在二维平面,会导致有机分子的手性以及吸附构型对反应产物具有重要影响,增加了调控化学反应的自由度,因此可以合成传统溶液化学中难以得到的一些高分子和纳米结构.3.1 节和3.2 节将详细介绍两种不同的合成方法.
3.1 “自下而上”的搭积木合成方法
近10 年来,通过深度融合有机化学合成、表面化学以及扫描探针表征技术,发展了一类普适的精准制备低维石墨烯材料的新方法.如图5(a)所示,该方法利用“自下而上”的策略,类似于搭积木,可以搭建出任意形状的低维石墨烯材料.首先,利用溶液合成方法合成具有特定官能基团的分子前驱体;然后,借助表面化学合成手段沉积分子前驱体到原子级平整表面,逐步诱导聚合反应和去环氢等反应,得到目标产物;最后,利用单化学键分辨的新型原子力显微镜技术,在实空间对目标产物的化学结构进行确认.该“自下而上”的方法具有诸多优势: 1) 通过改变前驱体分子,理论上可以合成任意结构的低维石墨烯结构,具有高度可调节性,能够实现单化学键精度的结构调控,为设计具有不同磁基态的石墨烯材料提供了重要支撑;2) 目标产物完全取决于前驱体分子,因此其尺寸大小、边缘结构是原子级精准的,整个结构无任何的缺陷.表面化学合成具有丰富的调控自由度,比如采用不同的化学反应方程[101-103]、激活化学反应的方式(热能、电子、光)[104-106]、衬底的模板效应[107-109]以及活化温度条件[110].从磁性纳米石墨烯结构设计的角度出发,这些丰富的调控自由度为设计具有更高自旋以及更为复杂的一维、二维磁性结构提供了可能性,或是将磁性纳米石墨烯与其他具有丰富物性的纳米结构桥接起来,从而产生更有趣的新的复合体系.图5(b)—(s)系统地总结了近年来利用表面化学合成的方法,研究制备了具有不同磁基态的纳米石墨烯[30-32,34-40,42,44,45,47-51].

图5 表面化学合成磁性纳米石墨烯 (a) 原理示意图;(b)—(s) 实验合成的不同磁基态纳米石墨烯[30-32,34-40,42,44,45,47-51] ((b)[36,42],(c)[32],(d)[39],(e)[37],(f)[30],(g)[31],(h)[44],(i)[45],(j)[47],(k)[35],(l)[50],(m) [38],(n)[38],(o)[34],(p)[49],(q)[40],(r)[48],(s)[51])Fig.5.On-surface synthesis of magnetic nano graphenes: (a) Schematic illustration of on-surface synthesis;(b)—(s) experimental synthesis results of nanographenes with different magnetic ground states[30-32,34-40,42,44,45,47-51].
3.2 针尖诱导表面反应
表面化学反应所需要的能量通常是以热能的方式提供,通过对衬底退火而自发诱导表面反应,得到目标结构.除了热退火,基于STM 发展出了通过STM 针尖诱导表面化学反应的方法,用隧穿电流中非弹性电子的能量损失代替热能作为表面化学反应的能量来源,可以逐步诱导反应,制备热反应没办法合成的中间产物.通常的做法是将针尖移动到分子上端合适的高度,通过施加一个合适的脉冲偏置电压来控制局部化学键的断裂与形成.如图6(a)所示,利用STM 的高空间分辨,可以实现单个化学键的操纵,比如早期的工作中可通过针尖诱导实现表面上人工的Ullmann 反应[111].在双层NaCl 表面通过针尖诱导实现了碳-碳共价键的反应[112]、脱卤素反应[101,113],以及逐步构建有机共价结构[113].针尖诱导表面反应的优势在于局域的精确可控,另外还可观察到一些表面反应的中间态.如图6(b)所示,在NaCl 表面首次通过针尖操纵诱导分子内部的Glaser 耦合反应,并且观测到了反应的中间产物[112].在绝缘体表面,针尖操纵实现局域的表面化学反应会变得更加容易,因为绝缘层将分子与金属衬底解耦合,隧穿电子在分子上的占据时间变得更长,有更大概率形成非弹性隧穿.但是,大部分有机分子与绝缘衬底的吸附相较于金属衬底更弱,在针尖操纵过程中很容易改变吸附构型从而偏离针尖前端,或是直接跳跃吸附到针尖上.因此针尖操纵在绝缘体表面反应的实际效率反而会变低,难以用来构建大范围的磁性纳米石墨烯结构.

图6 STM 针尖诱导表面反应 (a) Ullmann 反应[111];(b) Glaser 耦合的中间态[112];(c) 针尖诱导去氢反应示意图[29];(d)—(g) 纳米石墨烯中针尖诱导去氢反应,并逐步获得高自旋 [29,34,37,39] ((a),(b),(d),(e)出自文献[111,112,29,39],已获得授权)Fig.6.STM tip-driven on surface reactions: (a) Ullmann reaction[111];(b) Glaser coupling and intermediates[112];(c) schematic illustration of tip-driven on surface dehydrogenation[29];(d)—(g) tip-driven dehydrogenation in nanographenes and high spins states in the same nanographene are available step by step [29,34,37,39] ((a),(b),(d),(e) reproduced with permission from Ref.[111,112,29,39]).
研究发现 sp3杂化的碳原子能抑制纳米石墨烯的磁性[29,37,39],主要原因是sp3杂化的碳原子改变了体系整体的π 电子数目[114].如图6(c)和图6(d)所示,三角烯在溶液合成中有多种副产物,其中一种是具有两个sp3杂化碳原子.通过针尖操纵可以将sp3碳原子的碳氢键打断使其恢复到sp2杂化,从而恢复纳米石墨烯的磁性,这是首次获得三角烯采用的方法[29].图6(e)和图6(f)显示,通过针尖操纵去氢过程可实现纳米石墨烯磁基态从S=0,1/2 到S=1 的转变.图6(g)是将一端被氢钝化的Clar’s goblet 从S=1/2 还原到自旋单态S=0 的磁基态.由此可见,纳米石墨烯的磁性被H原子钝化是常见的现象,而针尖操纵去氢反应在金属衬底也容易实现,可有效恢复分子的磁性[34,37,39].同时,逐步诱导去氢反应可以逐步控制纳米石墨烯的自旋数目,这有利于在同一个体系中追踪磁基态的变化.
另外,针尖操纵还可以移除其他一些保护基团[115].例如上述Ullmann 反应中针尖操纵可以移除卤素原子,并苯合成中可以移除氧原子和双酮基基团[106,116],在石墨烯纳米带中,可以移除Armchair边缘修饰的酮基[83],而Zigzag 边缘修饰的酮基则难以被针尖操纵移除[84].这些丰富的可操纵的基团为磁性纳米石墨烯的设计提供了更多的自由度.综上所述,表面化学合成是获得π 磁性纳米石墨烯的主要手段,通过合理的前驱体分子设计,可以在金属表面成功构建基于π 电子磁性的低维石墨烯结构.表面化学合成的原子级精确优势,与表面敏感表征技术的契合,为研究纳米石墨烯π 电子磁性提供了良好的平台.
4 表征低维磁性纳米石墨烯系统
利用STM 技术,可以精准地测量纳米石墨烯的磁基态.例如,纳米石墨烯的净磁矩和金属传导电子相互作用,将出现近藤效应;通过非弹性电子遂穿,可探测到自旋翻转谱;纳米石墨烯的净磁矩和超导库珀对相互作用,将出现Yu-Resinov-Shiba束缚态;利用自旋极化隧穿谱,可以直接测试自旋密度分布等.以下将从5 个方面讨论如何利用扫描隧道隧穿谱探测不同的磁性纳米石墨烯系统.
4.1 S=1/2 纳米石墨烯的近藤效应
如图7 所示,多类具有磁基态为S=1/2 的纳米石墨烯被合成,均在相关的体系中观测到了近藤效应,该行为可以很好地被安德森模型描述.安德森模型[117]描述了单个磁性杂质的半填充轨道电子与宿主金属连续能带电子之间的自旋相干散射.如图7(a)所示,S=1/2 的纳米石墨烯吸附在衬底金属表面,衬底金属的巡游电子会对表面上杂质自旋进行近藤散射,巡游电子与杂质自旋共同形成自旋单态,结果就是在费米面附近形成近藤共振峰,表现在STM 谱学上就是零偏压下尖锐的电导峰.近藤共振峰反映了纳米石墨烯自旋与金属衬底巡游电子之间的耦合强弱.共振峰可通过Frota 函数[118]拟合来获得半峰宽(half width at half maximum,HWHM),通过测量近藤共振峰随温度的响应,进一步基于费米液体模型[119]拟合HWHM 随温度的变化就可以得到纳米石墨烯的近藤温度TK.研究发现S=1/2 纳米石墨烯的近藤温度变化范围很广(最低6 K[32],最高141 K[35]),可能是由于这些S=1/2 自旋与衬底巡游电子之间的耦合强度存在很大变化,该耦合强度受分子结构和吸附构型影响.另外,通过外加磁场可以打破纳米石墨烯1/2 自旋的简并度,当磁场强度克服了近藤能量阈值时(kBTK),就可以看到近藤共振峰随磁场的塞曼劈裂,所需临界磁场大小可通过Bc≥0.5kBTK/gµb来估算[57].

图7 S=1/2 纳米石墨烯的近藤效应 (a) S=1/2 的近藤共振谱示意图;(b) 近藤共振峰的空间分布[36];(c) 近藤温度[36];(d) 近藤共振峰的塞曼劈裂[36];(e)—(i) 多种S=1/2 纳米石墨烯的近藤效应[32,35,40,41,49] ((b)—(i)出自文献[36,32,35,40,41,49],已获得授权)Fig.7.Kondo effect of S=1/2 nanographenes: (a) Schematic illustration of Kondo resonance spectroscopy of S=1/2;(b) spatial distribution of Kondo resonance peak[36];(c) Kondo temperature[36];(d) Zeeman splitting of Kondo resonance peak[36];(e)—(i) Kondo effect of various S=1/2 nanographenes[32,35,40,41,49] ((b)—(i) reproduced with permission from Ref.[36,32,35,40,41,49]).
4.2 高自旋的纳米石墨烯
对于单自旋S=1/2,其可完全被衬底的传导电子屏蔽掉,但对于高自旋系统,需要更多通道的电子来完全屏蔽高自旋磁矩.因此,当通道数少于自旋数时,整个系统将处于欠屏蔽(underscreened)区间.理论计算表明其近藤强度远低于完全屏蔽的单自旋情形,并且近藤共振态对磁场响应更加敏感[120-122].如图8 所示,高自旋S=1 的欠屏蔽现象在纳米石墨烯中被验证.利用表面化学合成方法制备了含两个sp3碳原子的纳米石墨烯,进而通过针尖操纵诱导去氢反应,在同一类纳米石墨烯中逐步实现了S=1/2 和S=1 两种磁基态.利用扫描隧道谱(scanning tunnel spectrum,STS),Pascual团队[37]和于平团队[39]分别观测到了S=1 高自旋的近藤屏蔽共振峰,该近藤峰的强度远低于完全屏蔽的S=1/2 近藤峰,和理论预期相符合.另外,该近藤峰对外加磁场更加敏感,其中S=1 近藤峰只需要较小的磁场就会发生劈裂.不同于单自旋,需要多个通道去完全屏蔽高自旋,这在Au 衬底表面并不会发生.根据Anderson 单个杂质模型,处于欠屏蔽区间的S=1,由于屏蔽效应的高度极化性,在B> 0 时近藤峰就会发生塞曼劈裂;而S=1/2 自旋则需要外加磁场产生的塞曼能量超过近藤屏蔽能量(kBTK)后才能够打开自旋简并度,也就是需要较大的磁场才能看到S=1/2 近藤共振峰的劈裂.除了高自旋S=1,实验上也合成出了具有更高自旋的磁性纳米石墨烯,例如S=3/2,2,3 等[30,31,44,45].在相关系统中,均没有观测到近藤屏蔽效应,一个可能原因是Au 表面没有足够的传导电子的通道去完全屏蔽更高自旋,导致其近藤强度低于实验检测的精度.
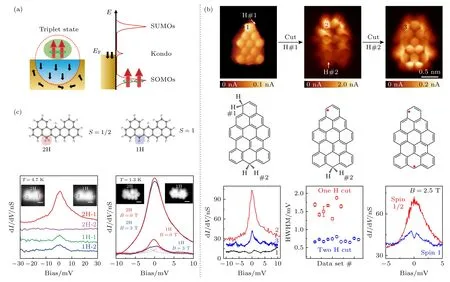
图8 高自旋纳米石墨烯的近藤效应 (a) S=1 自旋的近藤共振谱示意图;(b),(c) 同一个纳米石墨烯S=1/2 和S=1 的近藤效应[37,39] ((b),(c) 出自文献[37,39],已获得授权)Fig.8.Kondo effect of high spins nanographenes: (a) Schematic illustration of Kondo resonance spectroscopy of S=1;(b),(c) Kondo effect of S=1/2 and S=1 in the same nanographene[37,39] ((b),(c) reproduced with permission from Ref.[37,39]).
4.3 自旋单重态 (S=0)
自旋单重态的纳米石墨烯由于没有净磁矩,金属衬底的巡游电子不会产生近藤屏蔽,因此在STS 谱学上没有近藤共振峰.但自旋之间存在磁交换,交换能量大小可通过非弹性电子隧穿谱(inelastic electron tunneling spectroscopy,IETS)进行表征[69,123,124].部分电子在STM 针尖和样品之间隧穿时初态与末态发生改变,处于非弹性隧穿区间,自旋可以被这部分非弹性隧穿电子所翻转.让针尖位于其中一个自旋上方,逐渐提高隧穿电子的能量,当非弹性电子能量足够打破自旋间磁交换时,自旋状态将被激发从而打开新的隧穿通道,在STS 谱上表现为电导的阶梯式增加.自旋翻转只和隧穿电子的能量有关,在正负偏压下相同能量都会测到,因此自旋翻转谱通常具有U 型特征.如图9所示,实验上成功地合成了多类具有自旋单态的纳米石墨烯结构,并观测到了自旋翻转谱,其磁交换强度处于很大的范围(0—200 mV)[34-36,38,42,47,50].
从Hubbard 模型分析可得,自旋交换J来自库仑排斥作用,其强度与两个未配对π 电子的波函数交叠直接相关[125],满足:

其中,ϕ1,ϕ2表示两个磁性π 电子的单占据波函数.通过共价键相连接的纳米石墨烯,两端的未配对π 电子可以通过分子间碳-碳键的π 轨道进行自旋交换,那么连接处碳原子的自旋密度交叠就确定了磁交换的强弱.因此,控制磁性纳米石墨烯单占据波函数的交叠程度,可以实现不同强度的磁交换强度.图9 中的磁性纳米石墨烯,自旋交换强度均和(11)式描述的波函数交叠图像相吻合.

图9 自旋单重态纳米石墨烯的自旋交换 (a) S= 0 自旋单重态的自旋翻转谱示意图;(b)—(h) 不同纳米石墨烯的自旋交换J [34-36,38,42,47,50] ((b),(c),(f)—(h)出自文献[38,50,35,47],已获得授权)Fig.9.Spin exchange interaction of nanographenes with singlet ground state: (a) Schematic illustration of spin-flip spectroscopy of S= 0 singlet state;(b)—(h) spin exchange interaction J of different nanographenes with singlet ground state [34-36,38,42,47,50] ((b),(c),(f)—(h) reproduced with permission from Ref.[38,50,35,47]).
4.4 磁交换方向调控
磁交换的符号和强度均可以通过设计不同的连接方式来调控,实现铁磁耦合到反铁磁耦合的可控转变.对于半填充双子格体系,占据A格点的自旋与占据B格点的自旋直接共价连接时,库仑排斥会要求两个自旋占据相反的自旋态形成反铁磁耦合.如图10(a)所示,三角烯通过苯环形成二聚体,与苯环上不同位点的碳原子相连,二聚体的磁基态具有完全不同的形式: 1) 两个三角烯分别连接在苯环的不同子格位点,其磁基态为反铁磁耦合;2) 连接到同一套子格的不同位点,其磁基态为铁磁耦合[38].同样,将两个S=1/2 的三角烯额外通过两个碳原子连接成二聚体,翻转其中一个三角烯可以分别实现S=1 和S=0 的磁基态[38,39].通过控制分子内部碳碳键的形成,将属于同一套子格的碳原子连接起来,可以在不改变整体磁性的情况下局部地改变碳原子的自旋极化状态,进而在纳米石墨烯的二聚体中实现了铁磁基态和反铁磁基态,改变了π 电子自旋交换的符号[42].

图10 磁交换方向的调控 (a),(b) 联接方式改变纳米石墨烯磁基态[38,39];(c)—(e) AB 子格碳原子直联改变磁基态[42]((a)—(e) 出自文献[38,39,42],已获得授权)Fig.10.Controlling magnetic exchange direction: (a),(b) Change of magnetic ground states by different connecting configurations[38,39];(c)—(e) change of magnetic ground states by direct connecting two C atoms in AB sublattice respectively[42] ((a)—(e) reproduced with permission from Ref.[38,39,42]).
4.5 一维量子自旋链
量子自旋系统一直以来是量子关联多体系统中的一个重要领域.早在1931 年,Bethe[126]就研究了一维量子自旋S=1/2 反铁磁海森伯链,开辟了量子自旋链研究的篇章.对于高维情形下的反铁磁体,Anderson 等[127-129]在20 世纪50 年代发展了自旋波理论,研究发现自旋S=1/2 量子反铁磁海森伯链基态没有长程序.Haldane[130]在1983 年提出自旋为S的量子反铁磁海森伯模型应分为整数自旋和半奇整数自旋两个不同的普适类,整数自旋情形下体系具有有限能隙并在末端存在拓扑保护的自旋S=1/2 末端态.从实验的角度来看,中子散射等实验手段对自旋S=1 的准一维磁性材料进行了研究,Haldane 能隙被证实[131-134].但是固体材料中的大自旋通常需要Hund 相互作用产生,自旋S>2 的情形并不多见.另外,利用传统的谱学、输运测量,得到的是平均的信号.迄今为止,如何在实空间内制备高精度的研究低维量子磁性系统,一直是凝聚态实验物理方向的一个难点.
利用表面化学合成的优势,能够在表面构建一系列高度可调控的低维石墨烯量子自旋系统,利用超高分辨的表面探针探测技术、自旋极化探针手段、电子自旋共振技术,使得在实空间创制和研究低维自旋量子体系变为可能.如图11(a)所示,理论计算表明可以通过周期性地修饰纳米石墨烯,在其中周期性引入未配对的电子,构成一维S=1/2 自旋链[135,136].如图11(b)所示,周期性地利用B 元素替换C 元素进行掺杂,也可以在石墨烯纳米带中实现了一维量子自旋链[137-139].但是,实验上并未测试到相关系统中的量子自旋链的本征物性,其主要原因在于相邻自旋间的磁耦合太弱,超出了扫描遂穿谱的测试精度.2021 年,本课题组[48]和Fasel 团队[51]独立地构建出来了一维Haldane量子自旋链,并且观测到了分数化S=1/2 末端态.在S=1 的自旋链末端观测到S=1/2 的近藤共振峰(图11(c)中谱线1 和10[51],图11(d)中谱线1 和5[48]),而在自旋链内部则能看到两个末端自旋间单重态-三重态的有能隙激发,和Haldane理论预测相符合.利用相关方法,理论上可以构筑高度可调的量子磁性系统,为研究量子多体系统中的新奇物态提供一个新的舞台.
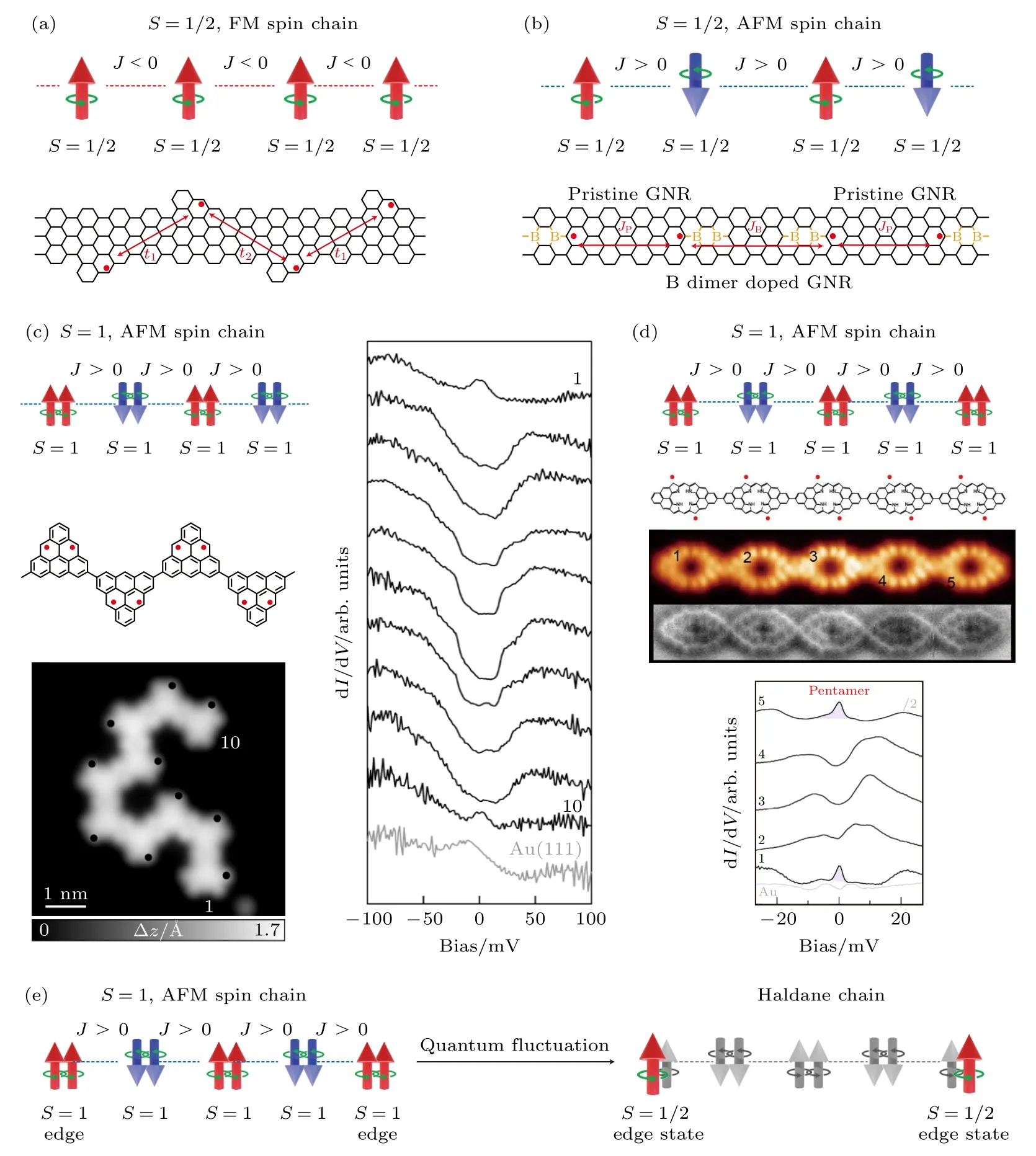
图11 纳米石墨烯构建一维量子自旋链 (a) S=1/2 铁磁链[136];(b) S=1/2 反铁磁链[138];(c) 基于三角烯构建S=1 反铁磁链[51];(d) 基于类卟啉纳米石墨烯构建S=1 反铁磁链[48];(e) Haldane 量子自旋链[48,51] ((c),(d) 出自文献[51,48],已获得授权)Fig.11.Building 1D quantum spin chains with magnetic nanographenes: (a) S=1/2 ferromagnetic spin chain[136];(b) S=1/2 antiferromagnetic spin chain[138];(c) S=1 antiferromagnetic quantum spin chain build with triangulene[51];(d) S=1 antiferromagnetic quantum spin chain build with porphyrins-based magnetic nanographenes[48];(e) Haldane quantum spin chain[48,51] ((c),(d) reproduced with permission from Ref.[51,48]).
5 总结与展望
本文综述了π 磁性纳米石墨烯的发展历程.从平均场近似的Habbard 模型出发解释了电子的多体相互作用是产生π 磁性的主要原因,并对其磁性起源进行了简要的归类.接着叙述了磁性纳米石墨烯的表面合成、针尖操纵的方法,以及对磁性表征的主要结果进行了讨论.这些研究充分展示了π 磁性纳米石墨烯的人工可控的优势,这类有机体系的磁性吸引人们去对其本身所具有的独特性质进行研究,同时也为人们构建丰富多彩的低维磁性系统搭建了良好的平台.未来有利于验证和构建基础物理研究中有趣的理论模型,并为新一代量子器件的设计和创造提供新的材料体系.
本文对纳米石墨烯π 磁性的研究做出以下展望: 1) 现阶段都是通过近藤效应和自旋翻转,间接证明纳米石墨烯的磁学性质.下一步需要利用自旋极化分辨技术[140],直接探测纳米石墨烯的自旋密度分布,提供更加直接的证据;2) 现有的磁性纳米石墨烯都是在金属表面合成.接下来,在绝缘衬底表面合成磁性纳米石墨烯就显得十分重要[141-143],并且易于与器件制备相结合,制备纳米石墨烯器件;3) 低维磁体和超导近邻作用将产生一系列有趣的现象,例如马约拉纳零能模[9]和Yu-Shiba-Rusinov束缚态[144-146].因此研究纳米石墨烯与超导的相互作用,将是接下来一个突破点.
